Wolfram Language Paclet Repository
Community-contributed installable additions to the Wolfram Language
Quantum Teleportation
Quantum teleportation is a communication protocol that sends quantum information to a distant party by utilizing a pre-shared pair of entangled particles (Bennett et al., 1993). The protocol has attracted public interest since it resembles (fictional) teleportation. In science fiction, (hypothetical) teleportation instantly transports matter or energy across space. Quantum teleportation does not transfer physical objects but only quantum information. Quantum teleportation is also conceptually distinguished from telefax. Telefax makes a copy of the document and sends the duplicated copy while the original document remains at its origin. In quantum teleportation, a quantum state is transferred and disappears from the original system.
Quantum teleportation is one of the first quantum information protocols that vividly illustrates the significance of quantum entanglement as a valuable resource. In this section, we discuss the physical principle behind quantum teleportation and demonstrate the protocol. Another closely related quantum communication protocol is the so-called superdense coding (Bennett and Wiesenr, 1992).
Quantum teleportation is not only interesting in its own right but also used as part of various quantum algorithms. Interestingly, even a computational model based solely on quantum teleportation has been proposed as well (Gottesman and Chuang, 1999; Nielsen, 2003; Leung, 2004).
Circuit representation of elementary gates. | |
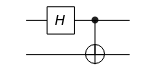
Two-qubit controlled-NOT gate. | |
Hadamard | The Hadamard gate. |
BellState | Returns a list of the four Bell states. |
Converts and operator (or Ket) expressions to the matrix representation in the standard basis. | |
Converts the matrix representation to the corresponding operator or state-vector expression. |
Functions related to the quantum teleportation protocol.
Make sure that the Q3 package is loaded to use the demonstrations in this document.
In[441]:=
Needs["QuantumMob`Q3`"]
Synopsis
Suppose that Bob wants to send one bit of quantum information, say, =+ stored in Charlie’s qubit, to Alice residing in a place far away from Bob (and Charlie). There is no quantum communication channel operating between Alice and Bob to directly send the quantum state through. Fortunately, however, there is a classical commutation channel.
|ψ〉
C
|0〉
C
c
0
|1〉
C
c
1
|ψ〉
It is important to note that the quantum state is unknown. The no-cloning theorem prevents a naive approach such as copying and transmitting the quantum state.
|ψ〉
Simple Theory
In[444]:=
Needs["QuantumMob`Q3`"]
In[445]:=
Let[Qubit,S]Let[Complex,c]
To teleport a quantum state, Alice and Bob need to share an entangled pair of qubits in advance. Suppose that the shared pair of qubits is in the state , which is one of the four Bell states,
|〉
β
0
AB
|〉:=
β
0
|00〉+|11〉
2
|〉:=
β
1
|01〉+|10〉
2
|〉:=
β
3
|01〉-|10〉
2
|〉:=
β
3
|00〉-|11〉
2
In[447]:=
bs=BellState[S@{1,2}]
Out[447]=
,,,
+
0
S
1
0
S
2
1
S
1
1
S
2
2
+
0
S
1
1
S
2
1
S
1
0
S
2
2
-
0
S
1
1
S
2
1
S
1
0
S
2
2
-
0
S
1
0
S
2
1
S
1
1
S
2
2
Then, with the quantum state stored in qubit , that is,
C
|ψ〉
C
|0〉
C
c
0
|1〉
C
c
1
In[124]:=
msg=Ket[S[3]0]*c[0]+Ket[S[3]1]*c[1]
Out[124]=
c
0
0
S
3
c
1
1
S
3
the initial state of the overall three qubits at the beginning of the procedure is given by
|Ψ〉
|Ψ〉=⊗=
|〉
β
0
AB
|ψ〉
C
|000〉+|110〉+|001〉+|111〉
c
0
c
0
c
1
c
1
2
In[450]:=
in=bs〚1〛**msg
Out[450]=
c
0
0
S
1
0
S
2
0
S
3
2
c
1
0
S
1
0
S
2
1
S
3
2
c
0
1
S
1
1
S
2
0
S
3
2
c
1
1
S
1
1
S
2
1
S
3
2
Recall that Bob has qubits B and C at his hands.
In[451]:=
ProductForm[in,{S@1,S@{2,3}}]
Out[451]=
c
0
2
c
1
2
c
0
2
c
1
2
Rewriting the parts consisting of qubits B and C in the Bell basis, the basis consisting of the four Bell states, leads to
|Ψ〉=⊗+⊗+⊗+⊗
1
2
(|0〉+|1〉)
c
0
c
1
A
|〉
β
0
BC
1
2
(|0〉+|1〉)
c
1
c
0
A
|〉
β
1
BC
1
2
(|0〉-|1〉)
c
1
c
0
A
|〉
β
2
BC
1
2
(|0〉-|1〉)
c
0
c
1
A
|〉
β
3
BC
In[452]:=
prj=Dyad[#,#,S@{2,3}]&/@BellState[S@{2,3}];cmp=prj**in;cmp//KetFactor//TableForm
Out[454]//TableForm=
c 0 0 S 1 c 1 1 S 1 0 S 2 0 S 3 1 S 2 1 S 3 2 2 |
c 1 0 S 1 c 0 1 S 1 0 S 2 1 S 3 1 S 2 0 S 3 2 2 |
- c 1 0 S 1 c 0 1 S 1 0 S 2 1 S 3 1 S 2 0 S 3 2 2 |
c 0 0 S 1 c 1 1 S 1 0 S 2 0 S 3 1 S 2 1 S 3 2 2 |
The crucial point here is that the state of in the first term is identical to the original quantum state , and those in the rest are also closely related to by the Pauli operators. More explicitly, one can rewrite the total state vector as
A
|ψ〉
|ψ〉
|Ψ〉=⊗+⊗+⊗+⊗
|ψ〉
A
|〉
β
0
BC
(X|ψ〉)
A
|〉
β
1
BC
(Y|ψ〉)
A
|〉
β
2
BC
(Z|ψ〉)
A
|〉
β
3
BC
In[455]:=
out={1,S[1,1],I*S[1,2],S[1,3]}**cmp;KetFactor[out]//TableForm
Out[456]//TableForm=
c 0 0 S 1 c 1 1 S 1 0 S 2 0 S 3 1 S 2 1 S 3 2 2 |
c 0 0 S 1 c 1 1 S 1 0 S 2 1 S 3 1 S 2 0 S 3 2 2 |
c 0 0 S 1 c 1 1 S 1 0 S 2 1 S 3 1 S 2 0 S 3 2 2 |
c 0 0 S 1 c 1 1 S 1 0 S 2 0 S 3 1 S 2 1 S 3 2 2 |
Now Bob performs a measurement on the two qubits and , owned by Bob, in the Bell basis. The measurement will yield outcomes and will collapse the total state vector into the corresponding term, ⊗, where =I, =X, =Y, and =Z. The remaining task is for Bob to inform Alice of the outcome so that Alice recover the desired state by operating the inverse operator on her qubit. The information regarding the measurement outcome amounts to two bits, and it requires only a classical channel for transmission.
B
C
μ=0,1,2,3
(|ψ〉)
μ
S
A
|〉
β
μ
BC
0
S
1
S
2
S
3
S
μ
|ψ〉
μ
S
In short, the quantum teleportation protocol consists of the following steps:
1
.Alice and Bob generate an entangled pair of qubits, and , and share the pair between them. This can be done anytime before the procedure actually starts. Bob prepares a quantum state to send in a separate qubit .
A
B
C
2
.Bob makes a Bell measurement, i.e., the measurement in the Bell basis, on his two qubits and .
B
C
3
.Bob sends the two-bit information regarding the measurement outcome to Alice through a classical communication channel.
4
.Alice operates a proper inverse operator to recover the desired quantum state.
Preliminaries
In the quantum teleportation protocol, two essential parts are sharing entanglement and performing the Bell measurement. Before we demonstrate an implementation of the quantum teleportation protocol, here we summarize quantum circuit models of the two tasks.
Entangler Quantum Circuit
Entangler Quantum Circuit
In[33]:=
Needs["QuantumMob`Q3`"]
To establish an entanglement between two qubits initially in a product state, one needs to interact them. In the quantum circuit model, the interaction is achieve by the gate. Specifically, one can use the feature of the gate that copies the computational basis states of the control qubit to the target qubit,
(|0〉+|1〉)⊗|0〉=|00〉+|10〉↦|00〉+|11〉
c
0
c
1
c
0
c
1
c
0
c
1
The linear superposition of the control qubit may be built by the gate (a general form of linear superposition can be built with ).
Hadamard
In[460]:=
qc=QuantumCircuit[S[1,6],CNOT[S[1],S[2]]]
Out[460]=
Get the four Bell states applying the above quantum circuit to the product basis.
Bell-Measurement Circuit
Bell-Measurement Circuit
Implementation
Step 1. Alice and Bob generate and share an entangled pair using the quantum entangler circuit discussed above.
This is the quantum circuit that fulfills the tasks so far.
The overall state at this stage is as follows.
Step 2. Bob performs a Bell measurement on his qubits. This can be done by reversing the entangler circuit as explained in the above.
The overall quantum circuit so far is as follows.
This is the state of the total system expected at this stage.
Step 3. Bob sends the measurement outcome to Alice through a classical channel.
Step 4. Alice applies a proper unitary gate on her qubit in accordance with Bob’s message. These two steps are simulated by a feedback control.
Step 4. Alice applies a proper unitary gate on her qubit in accordance with Bob’s message. These two steps are simulated by a feedback control.
Combining all the steps, one can transmit a quantum state to a remote party without a quantum channel.
This is the final state of the total system.
Note that the Bell measurement outcomes are uniformed distributed, and the state resulting in Alice’s qubit is always the same as the original quantum state (msg) regardless of the measurement outcome.
Applications
As mentioned at the beginning, quantum teleportation is not only interesting in its own right but also used as part of various quantum algorithms. In fact, universal quantum computation based solely on quantum teleportation is possible (Gottesman and Chuang, 1999; Nielsen, 2003; Leung, 2004). For photonic quantum computers, this is vital because photons do not interact with each other and hence the CNOT gate is impossible with usual linear optics (Knill, Laflamme, and Milburn, 2001).
Figure 1: A quantum circuit to realize the CNOT gate using quantum teleportation. The first and last qubits are the control and target qubits, respectively, and the result is stored in the third and forth qubits, respectively. Here, the two Bell measurements (between the vertical dashed lines) are implemented through the usual gate operations and measurements in the computational basis. In realistic situations, however, they are achieved (non-deterministically in many cases) using special measurement devices (such as parity measurement).
First, generate the entanglement in the ancillary quantum register.
Here is the core part of the quantum circuit to implement the CNOT gate using quantum teleportation.
Let us construct a small subroutine to facilitate the test of the above quantum circuit.