Wolfram Language Paclet Repository
Community-contributed installable additions to the Wolfram Language
Kitaev Random Circuit  |  |
Here, the effects of random measurements on the entanglement in the Kitaev chain of Majorana fermions is investigated. A realization of such Kitaev random circuit is shown in Figure 1.
Figure 1. A typical form of Kitaev random circuit. Each line indicates a fermion mode, the unitary gate with label denotes the time-evolution of Kitaev's model of Majorana fermions, and the measurement symbols depict the measurement of occupation number of the fermion modes.
U
This demonstration page was motivated by the phenomenon of measurement-induced entanglement transition, a transition between two distinct phases with the entanglement entropy characterized by area- and volume-law scaling. See also Li, Chen, and Fisher (2018), Skinner, Ruhman, and Nahum (2019), Chan et. al. (2019), Sang et al. (2021), and Weinstein, Bao, and Altman (2022).
Represents a fermionic Gaussian state | |
Represents a Gaussian-type unitary operator | |
Represents a set of quantum jump operators, which are linear compbinations of Majorana operators | |
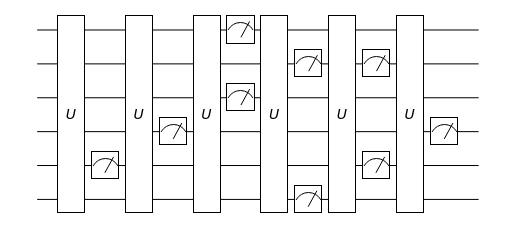
Rancomd quantum circuit consisting of fermionic gates. | |
Calculates the Green's functions with respect to a Wick state | |
Calculates the entanglement entropy in a Wick state | |
Calculates the logarithmic negativity in a Wick state |
Functions for fermionic quantum computation.
The Model
Make sure to load Q3.
In[173]:=
Needs["QuantumMob`Q3`"]
Set the number of fermion modes to consider.
In[174]:=
$n=6;
Choose a specific set of fermion modes for conversion between the conventional and Wick representations.
In[175]:=
Let[Fermion,c]cc=c[Range@$n]cccc=Join[cc,Dagger@cc];
Out[176]=
{,,,,,}
c
1
c
2
c
3
c
4
c
5
c
6
In[178]:=
HH=-μ*Q[cc]-t*PlusDagger[Hop@cc]+Δ*PlusDagger[Pair@cc]//Garner
Out[178]=
Examine the connectivity between neighboring fermion modes.
In[179]:=
GraphForm[HH]
Out[179]=
Extract the single-particle (or Bogoliubov-de Gennes) Hamiltonian (cf. many-body Hamiltonian in the above) of the model in the Nambu space. Notice the factor of 2.
In[180]:=
barH=2*CoefficientTensor[HH,Dagger@cccc,cccc];ArrayShort[barH,"Size"8]
Out[181]//MatrixForm=
-μ | -t | 0 | 0 | 0 | 0 | 0 | -Δ | … |
-t | -μ | -t | 0 | 0 | 0 | Δ | 0 | … |
0 | -t | -μ | -t | 0 | 0 | 0 | Δ | … |
0 | 0 | -t | -μ | -t | 0 | 0 | 0 | … |
0 | 0 | 0 | -t | -μ | -t | 0 | 0 | … |
0 | 0 | 0 | 0 | -t | -μ | 0 | 0 | … |
0 | Δ | 0 | 0 | 0 | 0 | μ | t | … |
-Δ | 0 | Δ | 0 | 0 | 0 | t | μ | … |
… | … | … | … | … | … | … | … | … |
Check that reproduces the original Hamiltonian (up to a constant).
1
2
†
c
H
c
In[182]:=
MultiplyDot[Dagger@cccc,barH.cccc]/2-HH//Garner
Out[182]=
3μ
To better understand the structure of the BdG Hamiltonian matrix, examine the single-particle and pairing blocks.
In[183]:=
blocks=PartitionInto[barH,{2,2}];ArrayShort[blocks]
Out[184]//MatrixForm=
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Setting up the model
Make sure to load Q3.
In[5]:=
Needs["QuantumMob`Q3`"]
Set the number of fermion modes to consider.
In[6]:=
$n=10;
Set the parameters.
In[7]:=
μ=0.2;t=Δ=1;
Directly construct the BdG Hamiltonian matrix (without using the fermion operator algebra as in the above section).
In[9]:=
hrm=-μ*One[$n]-t*PlusTopple@One[{$n,$n},1];del=-Δ*One[{$n,$n},1];del=del-Transpose[del];ham=NambuHermitian[{hrm,del}];ham//ArrayShort
Out[13]=
,
-0.2 | -1 | 0 | 0 | … |
-1 | -0.2 | -1 | 0 | … |
0 | -1 | -0.2 | -1 | … |
0 | 0 | -1 | -0.2 | … |
… | … | … | … | … |
0 | -1 | 0 | 0 | … |
1 | 0 | -1 | 0 | … |
0 | 1 | 0 | -1 | … |
0 | 0 | 1 | 0 | … |
… | … | … | … | … |
The time interval for each unitary layer to operate.
In[14]:=
$τ=3.;
Construct the single-particle unitary matrix.
In[15]:=
uv=NambuUnitary@MatrixExp[-I*Normal[ham]]
Out[15]=
NambuUnitary
 |
|
You can use the above unitary matrix in the Dirac spinor space (also known as the Nambu space). But it is slightly faster to first convert it to the equivalent matrix in the Majorana spinor space.
In[16]:=
wu=WickUnitary[uv](*orwu=ToMajorana[uv]*)
Out[16]=
WickUnitary
|
|
Prepare an initial state. A half-filling is a common choice.
In[17]:=
in=WickState[{1,0},$n]
Out[17]=
WickState
|
|
The probability to perform a measurement on each fermion mode.
In[18]:=
$p=.2;
The depth of quantum circuit.
Simulation
The simulation involves a lot of random number generators. To get the same result every time you open this document, set the seed of the random number generator.
Examine the structure of the resulting data.
Examine some of the output states as well.
Analysis
Each entry in data contains the information about one realization of quantum trajectory. Extract the trajectory history in an explicit form, for example, of the first entry.
In this particular case, there are 13 entries; the first entry is just the initial state and the rest are corresponds to the layers; there are 6 layers and each layer contains two sublayers of unitary evolution and measurements.
Note that the output states are all normalized.
Average Entanglement Entropy (EE)
Average Entanglement Entropy (EE)
For further analysis, take the subsystem. Below, we will consider entanglement properties between this subsystem and the rest.
Calculate the entanglement entropy.
Take the average of the entanglement entropy over different trajectories, and plot it as a function of time.
Average Logarithmic Negativity (LN)
Average Logarithmic Negativity (LN)
For further analysis, take the subsystem. This has been defined above; just in case.
Calculate the logarithmic negativity of each state in the particular trajectory.
Plot the entanglement (logarithmic negativity) as a function of time.
Logarithmic Negativity (LN) of Mixed States
Logarithmic Negativity (LN) of Mixed States
For further analysis, take the subsystem. This has been defined above; just in case.
Construct an approximate density matrix by taking average of covariance matrices in different trajectories.
Calculate the logarithmic negativity of the density matrices.
Plot the logarithmic negativity as a function of time..
Green's functions
Green's functions
For non-interacting fermion modes, most physical properties may be obtained from single-particle Green's functions or equivalently the Majorana covariance matrix.
N.B. Since Q3 v3.7.0, the output states in the WickState object contains the covariance matrix, and it is not necessary to calculate the Green's functions any longer.
Calculate the Green's functions between all fermion modes.