Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language
This resource function is obsolete. Use the paclet Wolfram/QuantumFramework instead.

Function Repository Resource:

 QuantumWignerTransform

Source Notebook

Convert quantum bases, states or operators in Hilbert space to functions in phase space

Contributed by: Jonathan Gorard and Ruhi Shah

ResourceFunction["QuantumWignerTransform"][QuantumBasis[…]]

performs a Wigner transform on the specified QuantumBasis, mapping from the Hilbert space picture to the phase space picture.

ResourceFunction["QuantumWignerTransform"][QuantumDiscreteState[…]]

performs a Wigner transform on the specified QuantumDiscreteState.

ResourceFunction["QuantumWignerTransform"][QuantumDiscreteOperator[…]]

performs a Wigner transform on the specified QuantumDiscreteOperator.

ResourceFunction["QuantumWignerTransform"][QuantumMeasurementOperator[…]]

performs a Wigner transform on the specified QuantumMeasurementOperator.

ResourceFunction["QuantumWignerTransform"][QuantumHamiltonianOperator[…]]

performs a Wigner transform on the specified QuantumHamiltonianOperator.

ResourceFunction["QuantumWignerTransform"][QuantumCircuitOperator[…]]

performs a Wigner transform on the operator representation of the specified QuantumCircuitOperator.

Details and Options

The Wigner–Weyl transform in quantum mechanics is the invertible map between operators on Hilbert space and functions in phase space. By convention, we take the Wigner transform to correspond to one direction of the map (from the Hilbert space picture to the phase space picture), and the Weyl transform to correspond to the other direction of the map (from the phase space picture to the Hilbert space picture).
ResourceFunction["QuantumWignerTransform"] will take a quantum object whose associated QuantumBasis is in the "Schrodinger" ("Schrödinger" and "Schroedinger" are also supported spellings), "Heisenberg" or "Interaction" picture, and transform it to one whose QuantumBasis is in the "PhaseSpace" picture.
ResourceFunction["QuantumWignerTransform"] will return a QuantumBasis object if the input was a QuantumBasis object, a QuantumDiscreteState object if the input was a QuantumDiscreteState object, etc. The only exception to this rule is the QuantumCircuitOperator object, whose Wigner transform is always a QuantumDiscreteOperator object (i.e. ResourceFunction["QuantumWignerTransform"] always returns the operator representation of the resulting circuit).
ResourceFunction["QuantumWignerTransform"] is defined for projection-valued QuantumMeasurementOperator objects, but not for positive operator-valued QuantumMeasurementOperator objects.
By default, ResourceFunction["QuantumWignerTransform"] will perform the Wigner transform using exact arithmetic.
With the option "Exact"→False, ResourceFunction["QuantumWignerTransform"] will perform the Wigner transform using numerical approximations instead. This usually improves performance when dealing with large states or operators.
The basis elements in the resulting orthonormal basis for the phase space picture are named W1,1,W1,2,….

Examples

Basic Examples (6) 

Compute the Wigner transform of a single-qubit Pauli-X QuantumBasis object to obtain a single-qubit QuantumBasis object in the phase space picture:

In[1]:=
basis = ResourceFunction["QuantumBasis"]["PauliX"]; basis["BasisElementAssociation"]
Out[1]=
In[2]:=
newBasis = ResourceFunction["QuantumWignerTransform"][basis]
Out[2]=
In[3]:=
newBasis["BasisElementAssociation"]
Out[3]=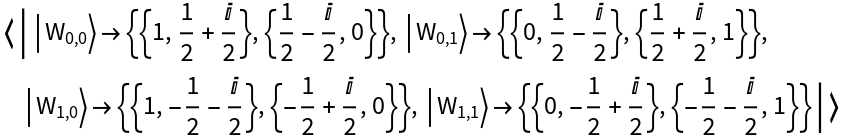

Compute the Wigner transform of a two-qubit Pauli-X QuantumBasis object to obtain a two-qubit QuantumBasis object in the phase space picture instead:

In[4]:=
basis2 = ResourceFunction["QuantumBasis"]["PauliX", 2]; basis2["BasisElementAssociation"]
Out[4]=
In[5]:=
newBasis2 = ResourceFunction["QuantumWignerTransform"][basis2]
Out[5]=
In[6]:=
newBasis2["BasisElementNames"]
Out[6]=

Compute the Wigner transform of an arity-1 QuantumDiscreteOperator object in the computational basis (default) to obtain a corresponding arity-1 QuantumDiscreteOperator object in the phase space picture:

In[7]:=
operator = ResourceFunction["QuantumWignerTransform"][ ResourceFunction["QuantumDiscreteOperator"]["Hadamard", {1}]]; operator["Operator"]
Out[7]=
In[8]:=
operator["Picture"]
Out[8]=

Compute the Wigner transform of an arity-2 QuantumDiscreteOperator object to obtain a corresponding arity-2 QuantumDiscreteOperator object in the phase space picture instead:

In[9]:=
operator2 = ResourceFunction["QuantumWignerTransform"][ ResourceFunction["QuantumDiscreteOperator"]["CNOT", {1, 2}]]; operator2["Operator"]
Out[9]=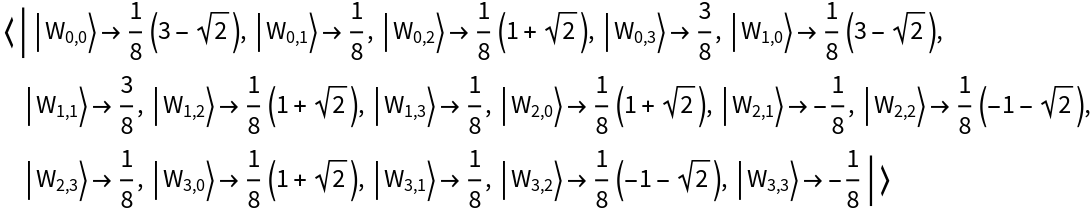
In[10]:=
operator2["Picture"]
Out[10]=

Compute the Wigner transform of an arity-2 projection-valued QuantumMeasurementOperator object in the computational basis (default) to obtain a corresponding arity-2 QuantumMeasurementOperator object in the phase space picture:

In[11]:=
operator = ResourceFunction["QuantumWignerTransform"][ ResourceFunction["QuantumMeasurementOperator"][ "FourierBasis", {1, 2}]]; operator["Operator"]
Out[11]=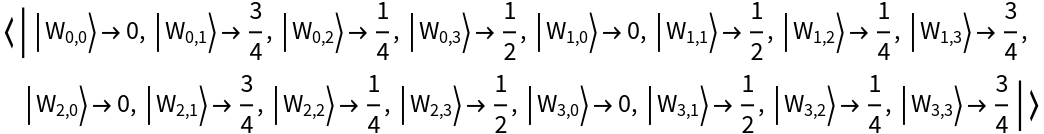

Compute the Wigner transform of an arity-1 QuantumHamiltonianOperator object in the computational basis (default) to obtain an arity-1 QuantumHamiltonianOperator object in the phase space picture:

In[12]:=
hamiltonian = ResourceFunction["QuantumWignerTransform"][ ResourceFunction[ "QuantumHamiltonianOperator"][{{1 + \[FormalT]^2, 1 - \[FormalT]^2}, {1 - \[FormalT]^2, 1 + \[FormalT]^2}}]]; hamiltonian["Operator"]
Out[12]=

Compute the Wigner transform of an arity-2 QuantumCircuitOperator object in the computational basis (default) to obtain an arity-2 QuantumDiscreteOperator object in the phase space picture:

In[13]:=
circuit = ResourceFunction[ "QuantumCircuitOperator"][{ResourceFunction[ "QuantumDiscreteOperator"]["CNOT", {1, 2}], ResourceFunction["QuantumDiscreteOperator"]["Hadamard", {2}], ResourceFunction["QuantumDiscreteOperator"]["SWAP", {1, 2}]}]; circuit["Diagram"]
Out[13]=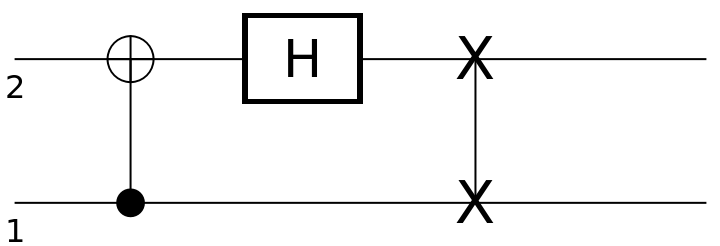
In[14]:=
operator = ResourceFunction["QuantumWignerTransform"][circuit]
Out[14]=

Show the operator association of the resulting QuantumDiscreteOperator:

In[15]:=
operator["Operator"]
Out[15]=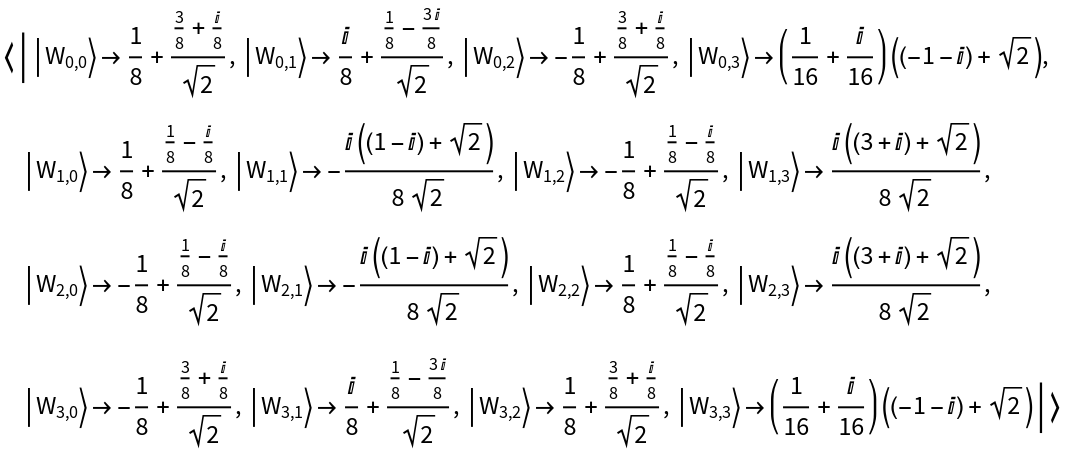

Compute the Wigner transform of a single-qubit QuantumDiscreteState object in the computational basis (default) to obtain a single-qudit 4-dimensional QuantumDiscreteState object in the phase space picture:

In[16]:=
state = ResourceFunction["QuantumWignerTransform"][ ResourceFunction["QuantumDiscreteState"][{1 + I/Sqrt[2], I + 1/Sqrt[2]}]]
Out[16]=
In[17]:=
state["Amplitudes"]
Out[17]=

Scope (2) 

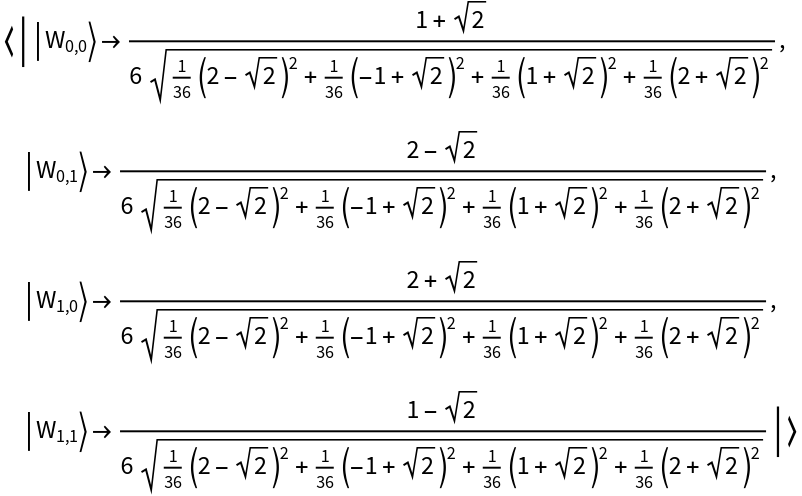Compute the Wigner transform of higher-dimensional quantum objects:

In[18]:=
state = ResourceFunction["QuantumWignerTransform"][ ResourceFunction["QuantumDiscreteState"][{1, 1 + I, 1 - I}, 3]]; state["Amplitudes"]
Out[18]=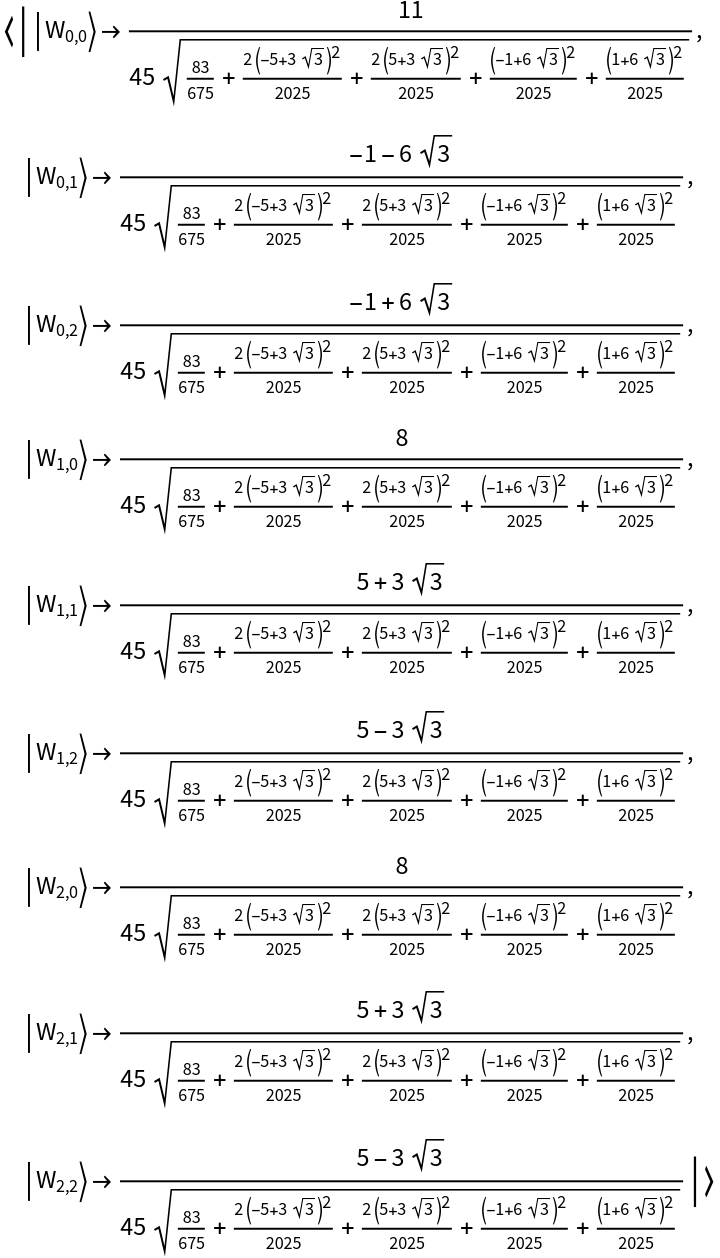
In[19]:=
state["Dimensions"]
Out[19]=

Wigner transforms can be computed for quantum objects in arbitrary bases:

In[20]:=
operator = ResourceFunction["QuantumDiscreteOperator"][ ResourceFunction["QuantumDiscreteOperator"]["Fourier", {1, 2}], ResourceFunction["QuantumBasis"]["PauliY", 2]]; operator["Basis"]
Out[20]=
In[21]:=
newOperator = ResourceFunction["QuantumWignerTransform"][operator]; newOperator["Basis"]
Out[21]=

However, the input object must be in either the "Schrodinger", "Heisenberg" or "Interaction" picture. If the input object is already in the "PhaseSpace" picture, then QuantumWignerTransform will not evaluate:

In[22]:=
ResourceFunction["QuantumWignerTransform"][newOperator]
Out[22]=

Options (2) 

By default, QuantumWignerTransform performs all computations using exact arithmetic:

In[23]:=
operator = ResourceFunction["QuantumWignerTransform"][ ResourceFunction["QuantumDiscreteOperator"]["Hadamard"]]; operator["Operator"]
Out[23]=

However, in some cases, performance can be improved by using the option "Exact"→False, in which case QuantumWignerTransform performs all computations using numerical approximations instead:

In[24]:=
operator2 = ResourceFunction["QuantumWignerTransform"][ ResourceFunction["QuantumDiscreteOperator"]["Hadamard"], "Exact" -> False]; operator2["Operator"]
Out[24]=

Publisher

Jonathan Gorard

Version History

  • 1.0.0 – 07 June 2021

Related Resources

License Information