Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Represent a quantum basis
ResourceFunction["QuantumBasis"][<|name1→b1,name2→b2,…|>,pic] represents a discrete quantum basis with basis elements bi, having names namei, with respect to the quantum mechanical picture pic. | |
ResourceFunction["QuantumBasis"]["name",pic] represents a named quantum basis "name", with respect to the quantum mechanical picture pic. | |
ResourceFunction["QuantumBasis"][{"name",d},pic] represents a d-dimensional version of a named quantum basis "name", with respect to the quantum mechanical picture pic. | |
ResourceFunction["QuantumBasis"][…,s] represents a specified quantum basis for a collection of s qudits (subsystems). | |
ResourceFunction["QuantumBasis"][ResourceFunction["QuantumBasis"][…],pic] transforms a specified quantum basis into the new quantum mechanical picture pic. |
| "BasisElementNames" | list of basis element names namei |
| "BasisElements" | list of basis elements bi |
| "NormalizedBasisElements" | list of normalized basis elements bi |
| "BasisElementAssociation" | the association <| name1→b1,name2→b2,…|> |
| "MatrixRepresentation" | change of basis matrix (from the computational basis) |
| "Rank" | tensor rank of the basis elements bi |
| "Type" | whether the basis elements bi are vectors, matrices or higher-rank tensors |
| "Dimensions" | dimensionality of the basis elements bi |
| "Qudits" | number of qudits (subsystems) in the basis |
| "Picture" | which quantum mechanical picture the basis is defined with respect to |
| "Properties" | list of all property names |
| "Computational" | 2-dimensional computational basis |
| {"Computational",d} | d-dimensional computational basis |
| "Bell" | Bell basis |
| "PauliZ" | Pauli-Z (computational) basis |
| "PauliX" | Pauli-X (Hadamard) basis |
| "PauliY" | Pauli-Y basis |
| "Fourier" | 2-dimensional basis of the quantum Fourier transform |
| {"Fourier",d} | d-dimensional basis of the quantum Fourier transform |
| "Schwinger" | 2-dimensional Schwinger basis |
| {"Schwinger",d} | d-dimensional Schwinger basis |
| "Pauli" | basis of the Pauli matrices |
| "Dirac" | basis of the Dirac (gamma) matrices |
| "Wigner" | 2-dimensional basis of the Wigner phase space operators with respect to the computational basis |
| {"Wigner",d} | d-dimensional basis of the Wigner phase space operators with respect to the computational basis |
| {"Wigner",ResourceFunction["QuantumBasis"][…]} | basis of the Wigner phase space operators with respect to the specified ResourceFunction["QuantumBasis"] |
Create a 2-dimensional basis in the Schrodinger picture (default), using Ket notation for the basis element names:
| In[1]:= |
| Out[1]= |
Return its basis element association:
| In[2]:= |
| Out[2]= |
Create a 2-dimensional basis in the Heisenberg picture, using strings for the basis element names:
| In[3]:= |
| Out[3]= |
Return its matrix representation (change of basis matrix):
| In[4]:= |
| Out[4]= |
Basis elements can be tensors of arbitrary rank:
| In[5]:= |
| Out[5]= |
Return a matrix representation:
| In[6]:= |
| Out[6]= |
Return the rank and type:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
Represent the Bell basis for a single qubit (default):
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= |
Represent the Bell basis for a pair of qubits (defined via a tensor product) instead:
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= | 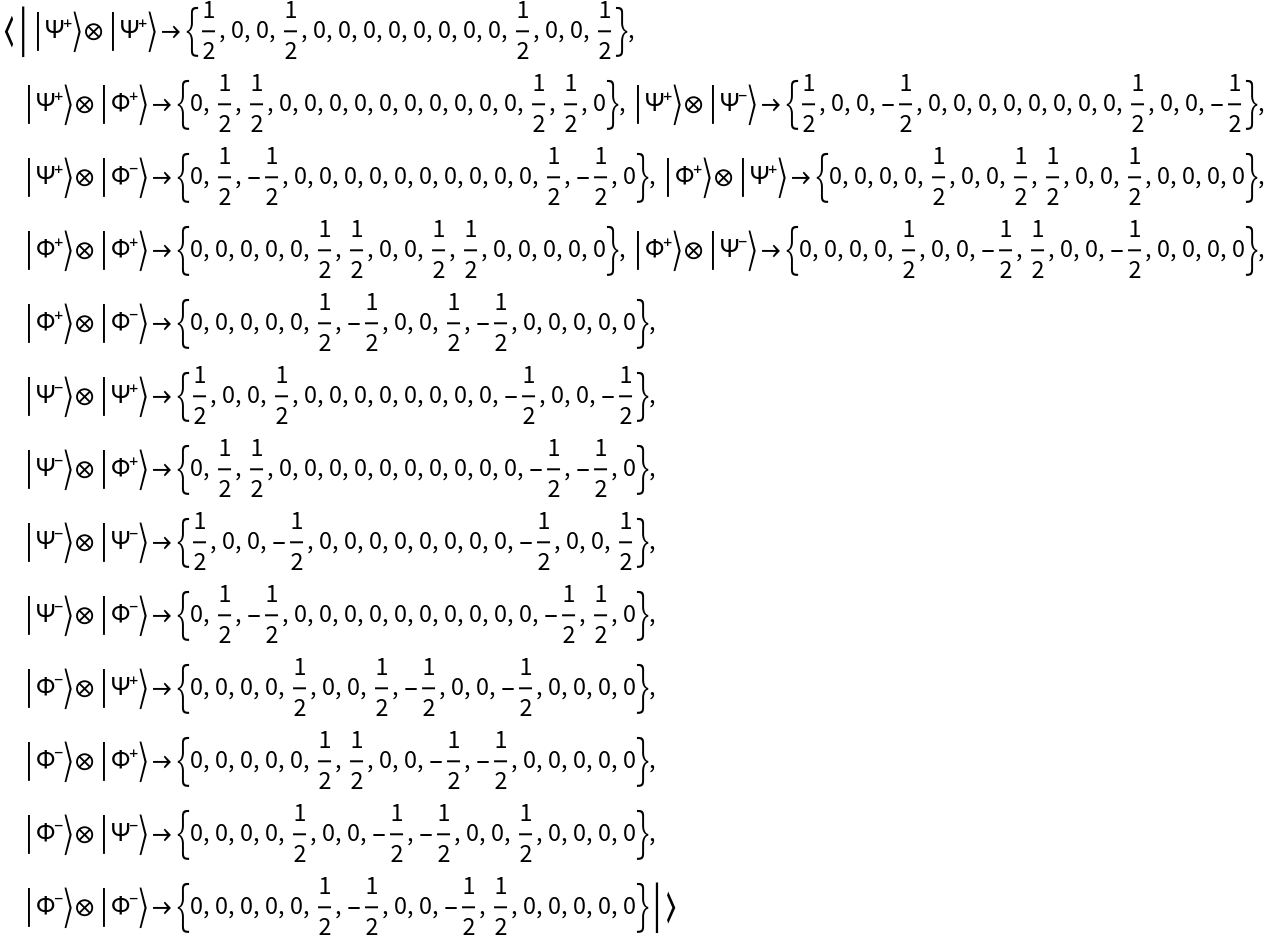 |
Represent the 2-dimensional (default) basis of the quantum Fourier transform:
| In[13]:= |
| Out[13]= |
Get its matrix representation:
| In[14]:= |
| Out[14]= |
Represent the 3-dimensional basis of the quantum Fourier transform instead:
| In[15]:= |
| Out[15]= |
Get its matrix representation:
| In[16]:= |
| Out[16]= | 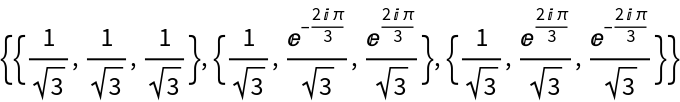 |
The elements of a 2-dimensional QuantumBasis can be arbitrary (potentially non-orthonormal) vectors:
| In[17]:= |
| Out[17]= |
Return the list of basis elements:
| In[18]:= |
| Out[18]= |
Return the list of normalized basis elements:
| In[19]:= |
| Out[19]= |
Represent the Pauli-X (Hadamard) basis in the Heisenberg picture:
| In[20]:= |
| Out[20]= |
Transform the basis to the interaction picture:
| In[21]:= |
| Out[21]= |
Create a 2-dimensional basis for a single qubit:
| In[22]:= |
| Out[22]= |
Create a 3-qubit version of the same basis by taking a tensor product of the basis with itself 3 times:
| In[23]:= |
| Out[23]= |
View the basis elements of the 3-qubit system:
| In[24]:= |
| Out[24]= | 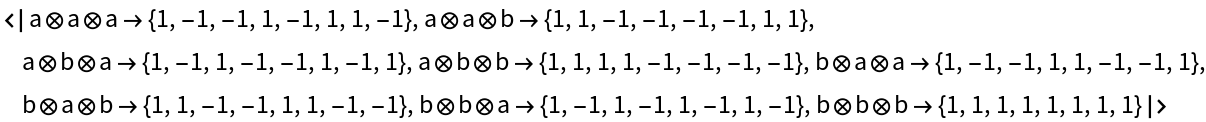 |
Represent the 2-dimensional Schwinger basis of rank-2 (matrix) elements:
| In[25]:= |
| Out[25]= |
View the basis elements:
| In[26]:= |
| Out[26]= |
Represent the 3-dimensional Schwinger basis:
| In[27]:= |
| Out[27]= |
View its basis elements:
| In[28]:= |
| Out[28]= | 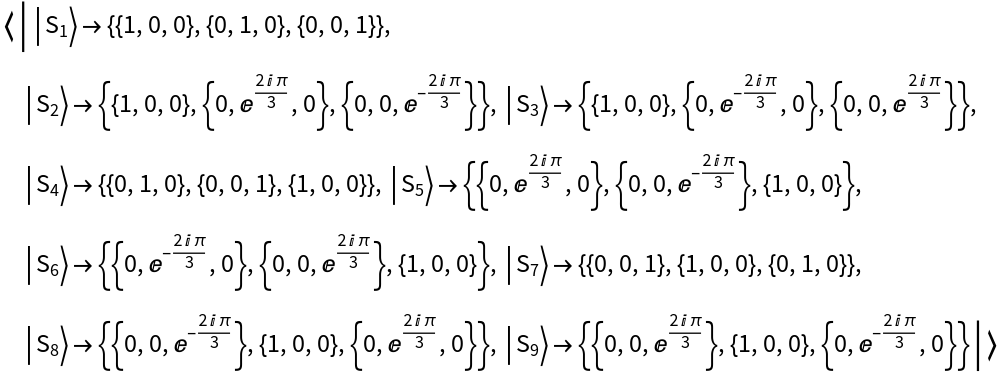 |
Represent the basis of rank-2 Pauli matrices:
| In[29]:= |
| Out[29]= |
View the basis elements:
| In[30]:= |
| Out[30]= |
Represent the basis of rank-2 Dirac (gamma) matrices:
| In[31]:= |
| Out[31]= |
View the basis elements:
| In[32]:= |
| Out[32]= | 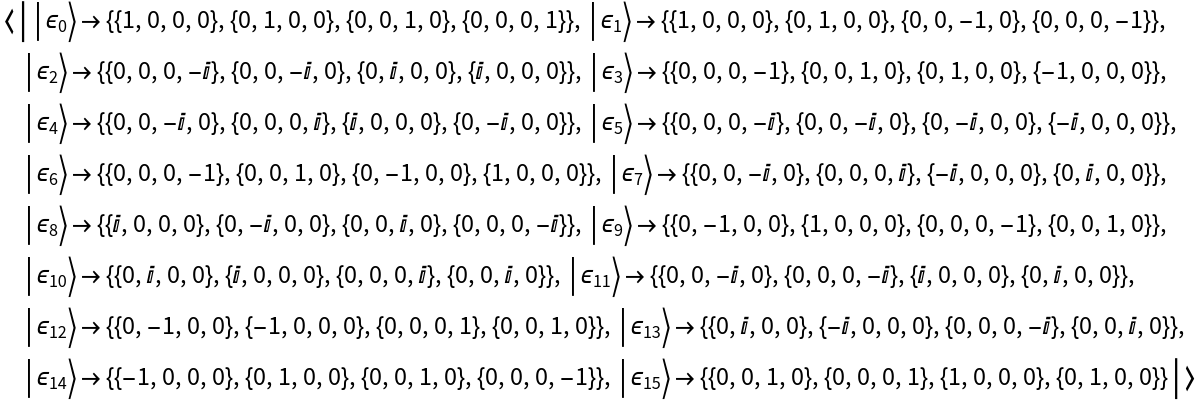 |
Represent the 2-dimensional basis of Wigner phase space operators with respect to the computational basis:
| In[33]:= |
| Out[33]= |
View the basis elements:
| In[34]:= |
| Out[34]= | 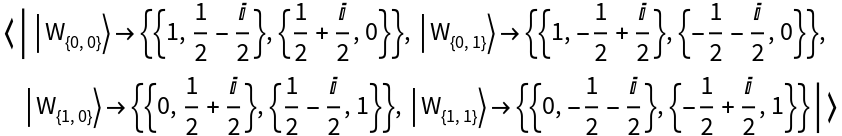 |
Represent the 3-dimensional basis of Wigner phase space operators with respect to the computational basis:
| In[35]:= |
| Out[35]= |
View the basis elements:
| In[36]:= |
| Out[36]= | 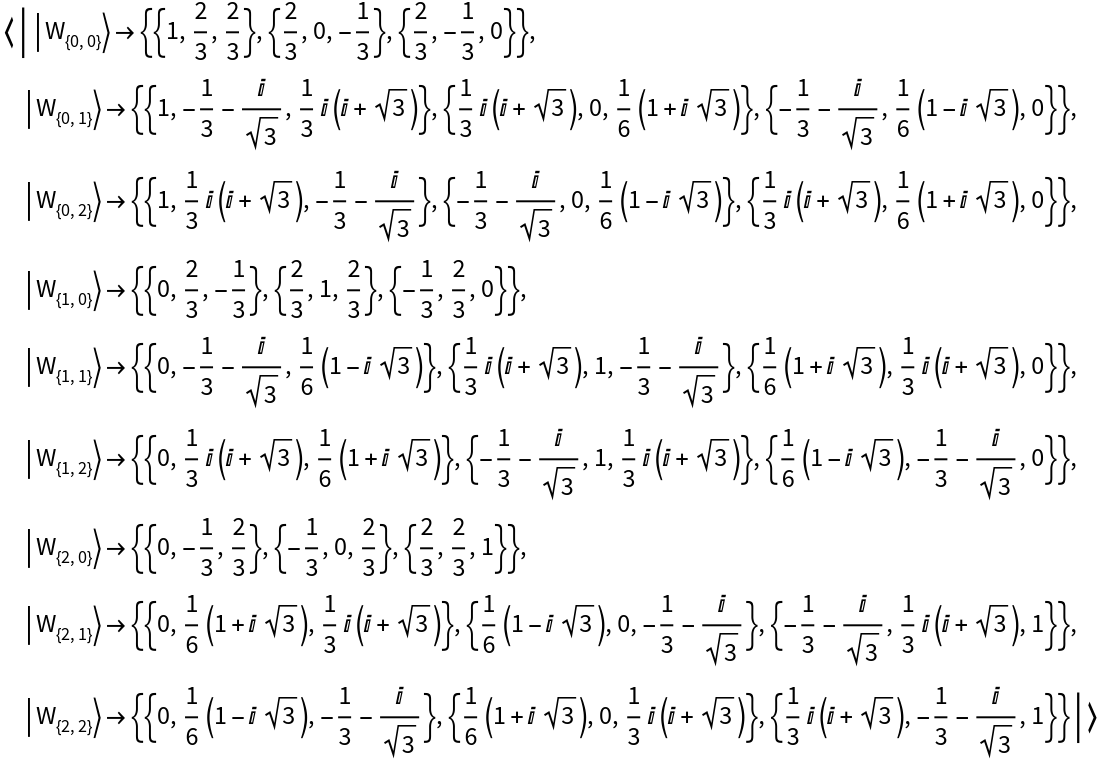 |
Represent the 2-dimensional basis of Wigner phase space operators with respect to the Pauli-X (Hadamard) basis:
| In[37]:= |
| Out[37]= |
View the basis elements:
| In[38]:= |
| Out[38]= | 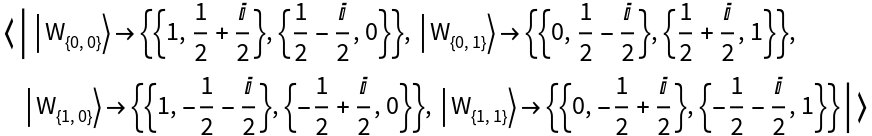 |
QuantumBasis objects can be constructed purely symbolically (without explicit vector or matrix elements):
| In[39]:= |
| Out[39]= |
View the basis elements:
| In[40]:= |
| Out[40]= |
Standard operations can still be performed on purely symbolic bases:
| In[41]:= |
| Out[41]= | 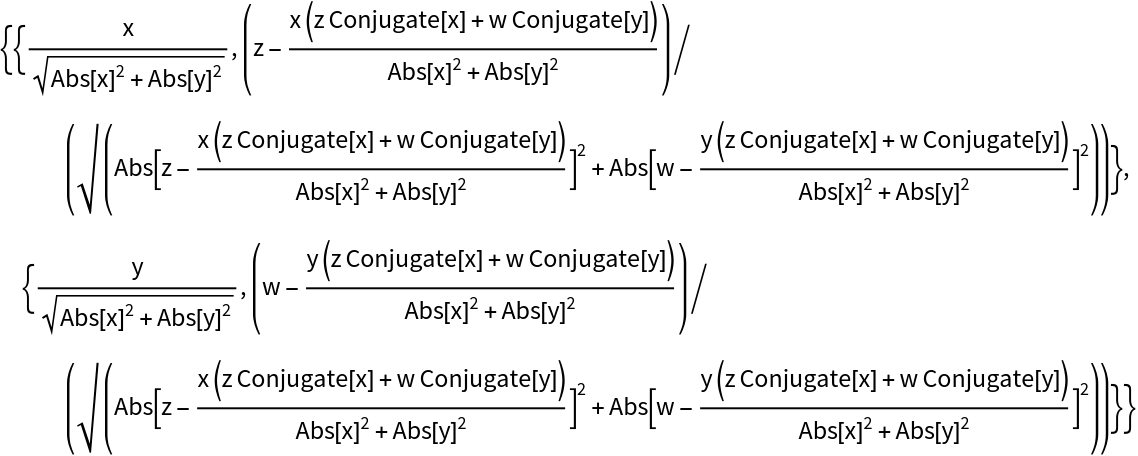 |
Represent a collection of 2 qudits:
| In[42]:= |
| Out[42]= |
View the basis elements:
| In[43]:= |
| Out[43]= |
View a list of properties that can be extracted from a QuantumBasis object:
| In[44]:= |
| Out[44]= |
| In[45]:= |
| Out[45]= |
Return the list of basis element names:
| In[46]:= |
| Out[46]= |
Return the list of basis elements:
| In[47]:= |
| Out[47]= |
Return the list of normalized basis elements:
| In[48]:= |
| Out[48]= |
Return the association of names and basis elements:
| In[49]:= |
| Out[49]= |
Return the matrix representation (change of basis matrix):
| In[50]:= |
| Out[50]= |
Return the rank and type of basis:
| In[51]:= |
| Out[51]= |
| In[52]:= |
| Out[52]= |
Return the number of dimensions:
| In[53]:= |
| Out[53]= |
Return the number of qudits (subsystems):
| In[54]:= |
| Out[54]= |
Return which quantum mechanical picture the basis is defined with respect to:
| In[55]:= |
| Out[55]= |
This work is licensed under a Creative Commons Attribution 4.0 International License