This resource function is obsolete. Use the paclet Wolfram/QuantumFramework instead.

Function Repository Resource:

QuantumHamiltonianOperator

Represent a quantum Hamiltonian operator

Contributed by: Jonathan Gorard and Ruhi Shah (with modifications by Taufiq Murtadho)

ResourceFunction["QuantumHamiltonianOperator"][{<|b₁₁→e₁₁,b₁₂→e₁₂,…|>,p,p_min,p_max,p_step},order,QuantumBasis[…]]

represents a quantum Hamiltonian operator with (tensor products of) basis elements b_ij and associated matrix elements e_ij, with evolution parameter p, initial parameter value p_min, final parameter value p_max, parameter step p_step, applied to the qudits indexed by order, defined with respect to a specified QuantumBasis.

ResourceFunction["QuantumHamiltonianOperator"][{mat,p,p_min,p_max,p_step},order,QuantumBasis[…]]

represents a quantum Hamiltonian operator with matrix representation mat..

ResourceFunction["QuantumHamiltonianOperator"][{"name",p,p_min,p_max,p_step},order,pic]

represents a named quantum Hamiltonian operator "name".

ResourceFunction["QuantumHamiltonianOperator"][{"name",d,p,p_min,p_max,p_step},order,pic]

represents a d-dimensional version of a named quantum Hamiltonian operator.

ResourceFunction["QuantumHamiltonianOperator"][{QuantumDiscreteOperator[…],p,p_min,p_max,p_step},order,pic]

represents a quantum Hamiltonian operator whose associated evolution operator (i.e. the associated solution to the Schrödinger equation) is the specified QuantumDiscreteOperator.

ResourceFunction["QuantumHamiltonianOperator"][{mat_i→mat_f,p,p_min,p_max,p_step},order,pic]

represents a quantum Hamiltonian operator that linearly interpolates between the matrix representations mat_i (at p=p_min) and mat_f (at p=p_max).

ResourceFunction["QuantumHamiltonianOperator"][ResourceFunction["QuantumHamiltonianOperator"][…],QuantumBasis[…]]

transforms a specified ResourceFunction["QuantumHamiltonianOperator"] into a new QuantumBasis.

ResourceFunction["QuantumHamiltonianOperator"][ResourceFunction["QuantumHamiltonianOperator"][…],pic]

transforms a specified ResourceFunction["QuantumHamiltonianOperator"] into the new quantum mechanical picture pic.

Details

The QuantumBasis object is produced by the resource function QuantumBasis. When a QuantumBasis object is not specified, the default is taken to be QuantumBasis["Computational"].

When an evolution parameter p is not specified, the default is taken to be the formal symbol t. Likewise, when initial and final parameter values p_min and p_max are not specified, the defaults are taken to be p_min=0 and p_max=1, respectively. Finally, when a parameter step p_step is not specified, the default is taken to be p_step=(p_max-p_min)/100.

When an order order is not specified, the default is taken to be Range[arity], where arity designates the arity of the ResourceFunction["QuantumHamiltonianOperator"].

The permitted values of pic in ResourceFunction["QuantumHamiltonianOperator"][…,pic] are "Schrodinger" (default), which may also be written "Schroedinger" or "Schrödinger", "Heisenberg", "Interaction" and "PhaseSpace".

ResourceFunction["QuantumHamiltonianOperator"][{<|b₁₁→e₁₁,b₁₂→e₁₂,…|>,p,p_min,p_max,p_step},d,order] and ResourceFunction["QuantumHamiltonianOperator"][{mat,p,p_min,p_max,p_step},d,order] are used to represent a quantum Hamiltonian operator in the computational basis, specified by the Association <|b₁₁→e₁₁,b₁₂→e₁₂,…|> or the matrix mat, consisting of qudits of dimensionality d. When d is not specified, the default is taken to be 2.

The Association <|b₁₁→e₁₁,b₁₂→e₁₂,…|> has keys given by (tensor products of) named based elements b_ij and values given by matrix elements e_ij (i.e. entries in the corresponding matrix representation). The order order is always a list of positive integers.

When taken as a specification of a quantum evolution, ResourceFunction["QuantumHamiltonianOperator"][{…,p,p_min,p_max,p_step},…] signifies that the evolution parameter p (often interpreted as time) evolves from its initial value p=p_min to its final value p=p_max in discrete steps of p_step.

ResourceFunction["QuantumHamiltonianOperator"][…]["prop"] gives the property "prop" of the specified quantum Hamiltonian operator. Possible properties include:

"Operator"

association <|b₁₁→e₁₁,b₁₂→e₁₂,…|> of tensor products of basis names and matrix elements

"Basis"

which QuantumBasis the Hamiltonian operator is defined with respect to

"Picture"

which quantum mechanical picture the Hamiltonian operator is defined with respect to

"BasisElements"

list of basis elements b_i

"Parameter"

evolution parameter p

"InitialParameter"

initial value of the evolution parameter p_min

"FinalParameter"

final value of the evolution parameter p_max

"ParameterStep"

size of discrete step for the evolution parameter p_step

"MatrixRepresentation"

matrix representation mat of the Hamiltonian operator (including dependence upon the evolution parameter p)

{"MatrixRepresentation",p_val}

matrix representation mat of the Hamiltonian operator with the evolution parameter set to p=p_val

"InitialMatrixRepresentation"

matrix representation mat of the Hamiltonian operator with the evolution parameter set to the initial value p=p_min

"FinalMatrixRepresentation"

matrix representation mat of the Hamiltonian operator with the evolution parameter set to the final value p=p_max

"OrderedMatrixRepresentation"

matrix representation adjusted according to the order of the Hamiltonian operator (including dependence upon the evolution parameter p), assuming an input state containing Max[order] qudits (subsystems)

{"OrderedMatrixRepresentation",n}

matrix representation adjusted according to the order of the Hamiltonian operator (including dependence upon the evolution parameter p), assuming an input state containing n qudits (subsystems)

{{"OrderedMatrixRepresentation",n},p_val}

matrix representation adjusted according to the order of the Hamiltonian operator with the evolution parameter set to p=p_val, assuming an input state containing n qudits (subsystems)

"InitialOrderedMatrixRepresentation"

matrix representation adjusted according to the order of the Hamiltonian operator with the evolution parameter set to the initial value p=p_min, assuming an input state containing Max[order] qudits (subsystems)

{"InitialOrderedMatrixRepresentation",n}

"FinalOrderedMatrixRepresentation"

matrix representation adjusted according to the order of the Hamiltonian operator with the evolution parameter set to the final value p=p_max, assuming an input state containing Max[order] qudits (subsystems)

{"FinalOrderedMatrixRepresentation",n}

matrix representation adjusted according to the order of the Hamiltonian operator with the evolution parameter set to the final value p=p_max, assuming an input state containing n qudits (subsystems)

"Arity"

arity of the Hamiltonian operator

"Dimensions"

dimensionality of each qudit (subsystem) in the input state for the Hamiltonian operator

"Order"

order in which the Hamiltonian operator should be applied to qudits (subsystems) in the input state

"HermitianQ"

whether the Hamiltonian operator is Hermitian (self-adjoint)

"UnitaryQ"

whether the Hamiltonian operator is unitary (an automorphism of Hilbert space)

"Eigenvalues"

eigenvalues of the matrix representation of the Hamiltonian operator

"Eigenvectors"

eigenvectors of the matrix representation of the Hamiltonian operator

"MinimumGap"

minimum gap between the first two eigenvalues of the Hamiltonian operator (minimized over all possible values of the evolution parameter p)

"InitialGap"

initial gap between the first two eigenvalues of the Hamiltonian operator (with evolution parameter p=p_min)

"FinalGap"

final gap between the first two eigenvalues of the Hamiltonian operator (with evolution parameter p=p_max)

"Gap"

list of gaps between the first two eigenvalues of the Hamiltonian operator (for all possible values of the evolution parameter p)

{"Gap",p_val}

gap between the first two eigenvalues of the Hamiltonian operator with the evolution parameter set to p=p_val

"EvolutionOperator"

the corresponding evolution operator (i.e. the corresponding solution to the Schrödinger equation) represented as a QuantumDiscreteOperator (including dependence upon the evolution parameter p)

{"EvolutionOperator",p_val}

the corresponding evolution operator (i.e. the corresponding solution to the Schrödinger equation) represented as a QuantumDiscreteOperator with the evolution parameter set to p=p_val

"InitialEvolutionOperator"

the corresponding evolution operator (i.e. the corresponding solution to the Schrödinger equation) represented as a QuantumDiscreteOperator with the evolution parameter set to the initial value p=p_min

"FinalEvolutionOperator"

"Properties"

list of all property names

ResourceFunction["QuantumHamiltonianOperator"][{"name",…}] or ResourceFunction["QuantumHamiltonianOperator"][{"name",n,…}] represents an (n-qudit, unless otherwise specified) named quantum Hamiltonian operator. Possible named operators include:

"PauliX"

Hamiltonian operator based on the Pauli-X gate for qubits (equivalent to a π rotation around the x axis of the Bloch sphere)

{"PauliX",d}

Hamiltonian operator based on the Pauli-X gate for d-dimensional qudits (not Hermitian for general d>2)

"PauliY"

Hamiltonian operator based on the Pauli-Y gate for qubits (equivalent to a π rotation around the y axis of the Bloch sphere)

"PauliZ"

Hamiltonian operator based on the Pauli-Z gate for qubits (equivalent to a π rotationa round the z axis of the Bloch sphere)

{"PauliZ",d}

Hamiltonian operator based on the Pauli-Z gate for d-dimensional qudits (not Hermitian for general d>2)

{"Ising",coeffs}

Hamiltonian operator for the classical Ising model with upper-triangular coefficient matrix coeffs

{"TransverseIsing",coeffs}

Hamiltonian operator for the transverse-field Ising model with upper-triangular coefficient matrix coeffs

"RandomHermitian"

random Hermitian operator on qubits (Gaussian Hermitian ensemble)

{"RandomHermitian",d}

random Hermitian operator on d-dimensional qudits

{"LinearInterpolation",mat_i→mat_f}

Hamiltonian operator that linearly interpolates between matrix representations mat_i (at p=p_min) and mat_f (at p=p_max)

{"LinearInterpolation",qh₁→qh₂}

Hamiltonian operator that linearly interpolates between two ResourceFunction["QuantumHamiltonianOperator"] objects qh_i (at p=p_min and p=p_max, respectively)

{"LinearInterpolation",qd₁→qd₂]}

Hamiltonian operator that linearly interpolates between two associated evolution operators qd_i (i.e. associated solutions to the Schrödinger equation) at p=p_min and p=p_max, respectively

{"EvolutionOperator",mat}

Hamiltonian operator whose associated evolution operator (i.e. the associated solution to the Schrödinger equation) is represented by the matrix mat

{"EvolutionOperator",QuantumDiscreteOperator[…]}

Hamiltonian operator whose associated evolution operator (i.e. the associated solution to the Schrödinger equation) is the specified QuantumDiscreteOperator

ResourceFunction["QuantumHamiltonianOperator"][mat_i→mat_f] can be used as a shorthand for ResourceFunction["QuantumHamiltonianOperator"][{"LinearInterpolation",mat_i→mat_f}]; ResourceFunction["QuantumHamiltonianOperator"][ResourceFunction["QuantumHamiltonianOperator"][…]→ResourceFunction["QuantumHamiltonianOperator"][…]] can be used as a shorthand for ResourceFunction["QuantumHamiltonianOperator"][{"LinearInterpolation",ResourceFunction["QuantumHamiltonianOperator"][…]→ResourceFunction["QuantumHamiltonianOperator"][…]}]; ResourceFunction["QuantumHamiltonianOperator"][QuantumDiscreteOperator[…]→QuantumDiscreteOperator[…]] can be used as a shorthand for ResourceFunction["QuantumHamiltonianOperator"][{"LinearInterpolation",QuantumDiscreteOperator[…]→QuantumDiscreteOperator[…]}]; etc.

Likewise, ResourceFunction["QuantumHamiltonianOperator"][QuantumDiscreteOperator[…]] can be used as a shorthand for ResourceFunction["QuantumHamiltonianOperator"][{"EvolutionOperator",QuantumDiscreteOperator[…]}], etc.

Examples

Basic Examples (6)

Create a quantum Hamiltonian operator from a matrix representation in the computational basis (default), with evolution parameter t ranging from 0 to 1 in steps of 1/100 (default):

In[1]:=

$hamiltonian = ResourceFunction[ "QuantumHamiltonianOperator"][{{1 + \[FormalT]^2, 1 - \[FormalT]^2}, {1 - \[FormalT]^2, 1 + \[FormalT]^2}}]$

Out[1]=

Return its operator association:

In[2]:=

Out[2]=

Return its initial and final matrix representations (at t=0 and t=1, respectively):

In[3]:=

Out[3]=

In[4]:=

Out[4]=

Return its matrix representation at t=2/5:

In[5]:=

Out[5]=

Create a quantum Hamiltonian operator by linearly interpolating between two matrix representations in the computational basis (default), with evolution parameter t ranging from 0 to 1 in steps of 1/100 (default):

In[6]:=

Out[6]=

Return its associated evolution operator (i.e. the associated solution to the Schrödinger equation), with an explicit dependence on t:

In[7]:=

Out[7]=

In[8]:=

Out[8]=

Return the matrix representations of its initial and final evolution operators (at t=0 and t=1, respectively):

In[9]:=

Out[9]=

In[10]:=

Out[10]=

Return the matrix representation of its associated evolution operator at t=0.7:

In[11]:=

Out[11]=

Create a quantum Hamiltonian operator from a matrix representation in the computational basis (default), with evolution parameter x ranging from -1/2 to 1/2 in steps of 1/20, and return its operator association:

In[12]:=

$hamiltonian = ResourceFunction[ "QuantumHamiltonianOperator"][{{{(1 + \[FormalX])/ 2, (\[FormalX] - 1)/2}, {(\[FormalX] - 1)/2, (\[FormalX] + 1)/ 2}}, \[FormalX], -1/2, 1/2, 1/20}]; hamiltonian["Operator"]$

Out[12]=

Return its ordered matrix representation (assuming a state of size 2), with an explicit dependence on x:

In[13]:=

Out[13]=

Return its ordered matrix representation (assuming a state of size 3), with an explicit dependence on x:

In[14]:=

Out[14]=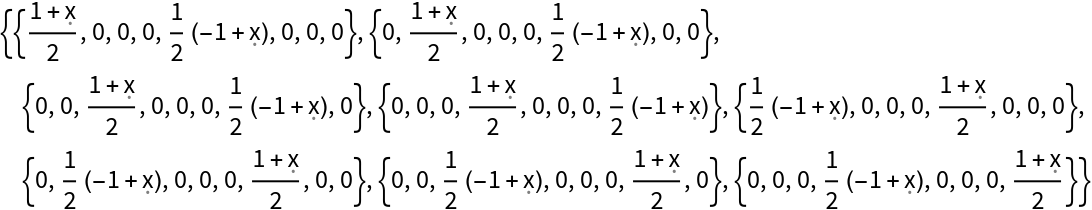

Return its initial and final ordered matrix representations (assuming a state of size 2), at x=-1/2 and x=1/2, respectively:

In[15]:=

Out[15]=

In[16]:=

Out[16]=

Return its ordered matrix representation (assuming a state of size 2), at x=1/4:

In[17]:=

Out[17]=

Create a quantum Hamiltonian operator from a matrix representation in a specified basis (Pauli-X), with evolution parameter x:

In[18]:=

$hamiltonian = ResourceFunction[ "QuantumHamiltonianOperator"][{{{(1 + \[FormalX])/ 2, (\[FormalX] - 1)/2}, {(\[FormalX] - 1)/2, (\[FormalX] + 1)/ 2}}, \[FormalX]}, ResourceFunction["QuantumBasis"]["PauliY"]]; hamiltonian["Operator"]$

Out[18]=

In[19]:=

Out[19]=

Transform the operator to the Fourier basis:

In[20]:=

hamiltonian2 = ResourceFunction["QuantumHamiltonianOperator"][hamiltonian, ResourceFunction["QuantumBasis"]["Fourier"]];
hamiltonian2["Operator"]

Out[20]=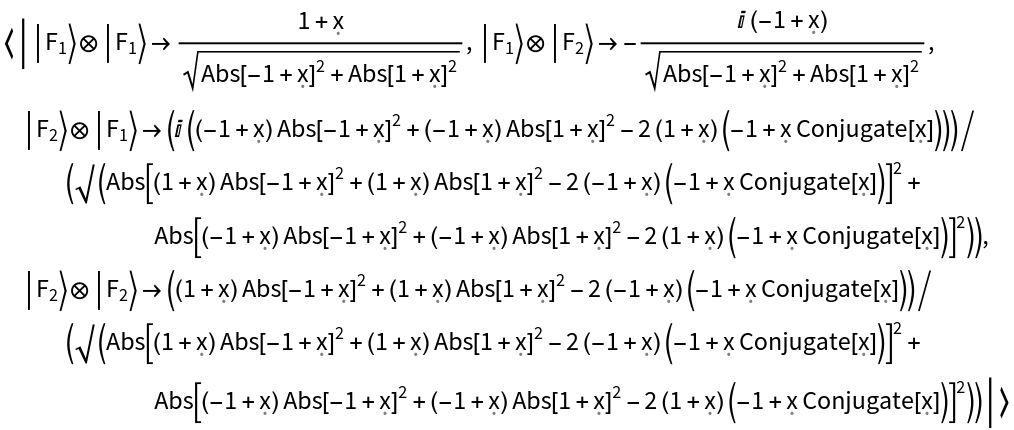

In[21]:=

Out[21]=

Create a quantum Hamiltonian operator by explicitly specifying an association of matrix elements in a given (tensor product) basis, with evolution parameter x, and return its matrix representation:

In[22]:=

$hamiltonian = ResourceFunction[ "QuantumHamiltonianOperator"][{<| TensorProduct[Ket[0], Ket[0]] -> I + \[FormalX], TensorProduct[Ket[0], Ket[1]] -> \[FormalX] - 1, TensorProduct[Ket[1], Ket[0]] -> \[FormalX] - I, TensorProduct[Ket[1], Ket[1]] -> 1 + \[FormalX]|>, \[FormalX]}, {1}]; hamiltonian["MatrixRepresentation"]$

Out[22]=

Return its basis element association:

In[23]:=

Out[23]=

Return its operator association:

In[24]:=

Out[24]=

Create a random Hermitian Hamiltonian operator for two qubits (default), applied to the second and fourth qubits respectively:

In[25]:=

Out[25]=

Create a random Hermitian Hamiltonian operator for one 3-dimensional qudit, applied to the fifth qudit:

In[26]:=

Out[26]=

Create an Ising Hamiltonian operator (i.e. a Hamiltonian for the classical ferromagnetic Ising model) from a simple upper-triangular coefficient matrix:

In[27]:=

Out[27]=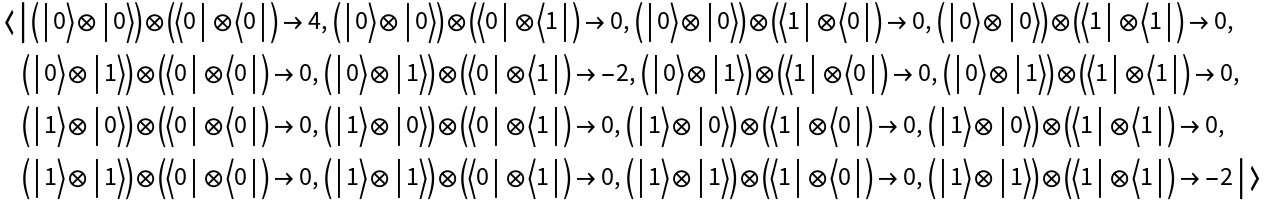

Create a transverse-field Ising Hamiltonian operator (i.e. a Hamiltonian for the quantum Ising model in a transverse magnetic field) from a simple upper-triangular coefficient matrix:

In[28]:=

Out[28]=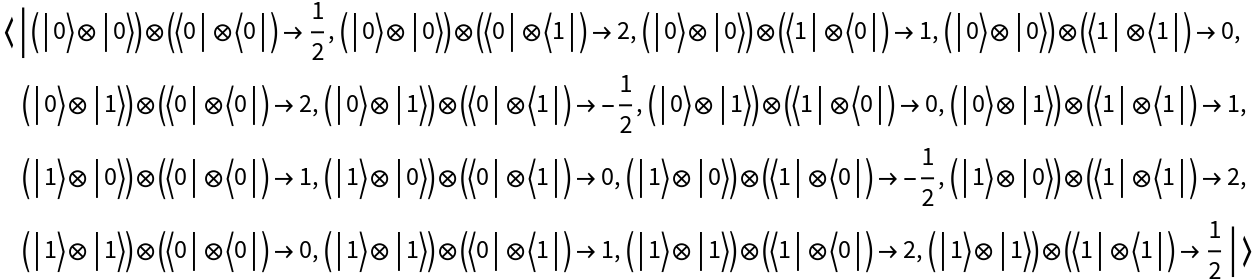

Scope (9)

By default, the evolution parameter is taken to be the formal symbol t:

In[29]:=

$hamiltonian = ResourceFunction[ "QuantumHamiltonianOperator"][{{1 + \[FormalT]^2, 1 - \[FormalT]^2}, {1 - \[FormalT]^2, 1 + \[FormalT]^2}}]; hamiltonian["Parameter"]$

Out[29]=

This choice can be overridden as follows:

In[30]:=

$hamiltonian2 = ResourceFunction[ "QuantumHamiltonianOperator"][{{{1 + \[FormalX]^2, 1 - \[FormalX]^2}, {1 - \[FormalX]^2, 1 + \[FormalX]^2}}, \[FormalX]}]; hamiltonian2["Parameter"]$

Out[30]=

By default, the initial and final parameter values are taken to be 0 and 1, respectively:

In[31]:=

Out[31]=

This choice can also be overridden as follows:

In[32]:=

$hamiltonian3 = ResourceFunction[ "QuantumHamiltonianOperator"][{{{1 + \[FormalX]^2, 1 - \[FormalX]^2}, {1 - \[FormalX]^2, 1 + \[FormalX]^2}}, \[FormalX], -100, 100}]; {hamiltonian3["InitialParameter"], hamiltonian3["FinalParameter"]}$

Out[32]=

Finally, by default, the parameter step is taken to be the difference between the initial and final parameter values, divided by 100:

In[33]:=

Out[33]=

This choice can also be overridden as follows:

In[34]:=

$hamiltonian4 = ResourceFunction[ "QuantumHamiltonianOperator"][{{{1 + \[FormalX]^2, 1 - \[FormalX]^2}, {1 - \[FormalX]^2, 1 + \[FormalX]^2}}, \[FormalX], -100, 100, 0.1}]; hamiltonian4["ParameterStep"]$

Out[34]=

Represent the Pauli-Z Hamiltonian operator in the Heisenberg picture:

In[35]:=

Out[35]=

In[36]:=

Out[36]=

Transform the Hamiltonian operator to the interaction picture:

In[37]:=

Out[37]=

In[38]:=

Out[38]=

Represent a 2-qubit random Hermitian Hamiltonian operator in the computational basis:

In[39]:=

Out[39]=

In[40]:=

Out[40]=

Represent the same Hamiltonian operator in the Pauli-X basis instead:

In[41]:=

hamiltonian2 = ResourceFunction["QuantumHamiltonianOperator"][hamiltonian, ResourceFunction["QuantumBasis"]["PauliX", 2]];
hamiltonian2["Operator"]

Out[41]=

In[42]:=

Out[42]=

Represent a Pauli-X Hamiltonian operator (a π rotation around the x axis of the Bloch sphere) on qubits for qubit number 3:

In[43]:=

Out[43]=

Represent a Pauli-X Hamiltonian operator on 3-dimensional qudits for qudit number 3 (not Hermitian):

In[44]:=

Out[44]=

Represent a Pauli-X Hamiltonian operator on 3-dimensional qudits for qudit number 3, with evolution parameter x ranging from -1 to 1 in steps of 1/10:

In[45]:=

$hamiltonian3 = ResourceFunction[ "QuantumHamiltonianOperator"][{"PauliX", 3, \[FormalX], -1, 1, 1/10}, {3}]; {hamiltonian3["Parameter"], hamiltonian3["InitialParameter"], hamiltonian3["FinalParameter"], hamiltonian3["ParameterStep"]}$

Out[45]=

Represent a Pauli-Y Hamiltonian operator (a π rotation around the y axis of the Bloch sphere) on qubits for qubit number 3:

In[46]:=

Out[46]=

Represent a Pauli-Z Hamiltonian operator (a π rotation around the z axis of the Bloch sphere) on qubits for qubit number 3:

In[47]:=

Out[47]=

Represent a Pauli-Z Hamiltonian operator on 3-dimensional qudits for qudit number 3 (not Hermitian):

In[48]:=

Out[48]=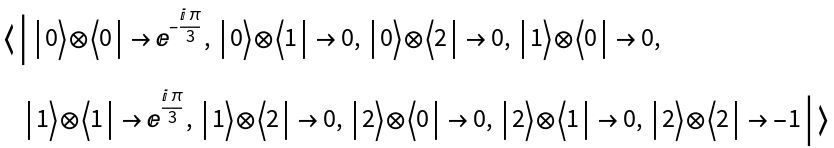

Represent an Ising Hamiltonian operator (i.e. a Hamiltonian for the classical ferromagnetic Ising model) with a simple upper-triangular coefficient matrix on two qubits, for qubits 2 and 3:

In[49]:=

Out[49]=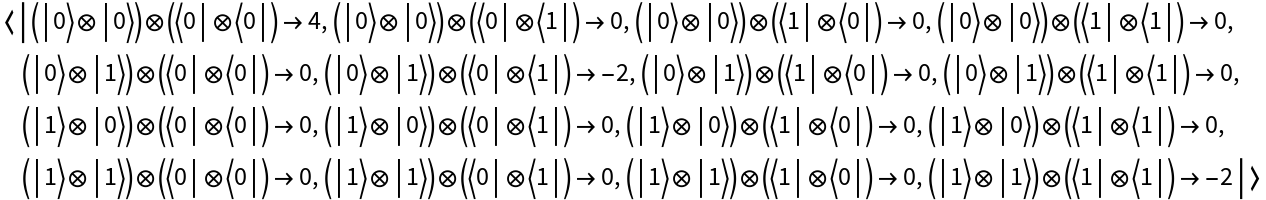

Represent an Ising Hamiltonian operator with a simple upper-triangular coefficient matrix on three qubits, for qubits 2, 3 and 4:

In[50]:=

Out[50]=

Represent an Ising Hamiltonian operator with a simple upper-triangular coefficient matrix on three qubits, for qubits 2, 3 and 4, with evolution parameter y ranging from -2 to 2 in steps of 1/20:

In[51]:=

$hamiltonian3 = ResourceFunction[ "QuantumHamiltonianOperator"][{"Ising", {{1, 1, 2}, {0, 2, 3}, {0, 0, 1}}, \[FormalY], -2, 2, 1/20}, {2, 3, 4}]; {hamiltonian3["Parameter"], hamiltonian3["InitialParameter"], hamiltonian3["FinalParameter"], hamiltonian3["ParameterStep"]}$

Out[51]=

Represent a transverse-field Ising Hamiltonian operator (i.e. a Hamiltonian for the quantum Ising model in a transverse magnetic field) with a simple upper-triangular coefficient matrix on two qubits, for qubits 2 and 3:

In[52]:=

Out[52]=

Represent a transverse-field Ising Hamiltonian operator with a simple upper-triangular coefficient matrix on three qubits, for qubits 2, 3 and 4:

In[53]:=

hamiltonian5 = ResourceFunction[
"QuantumHamiltonianOperator"][{"TransverseIsing", {{1, 1, 2}, {0, 2, 3}, {0, 0, 1}}}, {2, 3, 4}];
hamiltonian5["Operator"]

Out[53]=

Represent a single-qubit random Hermitian Hamiltonian operator (selected from a Gaussian Hermitian ensemble) for qubit 2:

In[54]:=

Out[54]=

Represent a two-qubit random Hermitian Hamiltonian operator (selected from a Gaussian Hermitian ensemble) for qubits 2 and 3:

In[55]:=

Out[55]=

Represent a single-qudit random Hermitian Hamiltonian operator (selected from a Gaussian Hermitian ensemble) on 3-dimensional qudits for qudit 2:

In[56]:=

Out[56]=

Represent a two-qudit random Hermitian Hamiltonian operator (selected from a Gaussian Hermitian ensemble) on 3-dimensional qudits for qudits 2 and 3:

In[57]:=

Out[57]=

Represent a two-qudit random Hermitian Hamiltonian operator (selected from a Gaussian Hermitian ensemble) on 3-dimensional qudits for qudits 2 and 3, with evolution parameter x ranging from -1 to 1 in steps of 1/10:

In[58]:=

$hamiltonian5 = ResourceFunction[ "QuantumHamiltonianOperator"][{"RandomHermitian", 3, \[FormalX], -1, 1, 1/10}, {2, 3}]; {hamiltonian5["Parameter"], hamiltonian5["InitialParameter"], hamiltonian5["FinalParameter"], hamiltonian5["ParameterStep"]}$

Out[58]=

Represent a linear interpolation between two Hamiltonian matrices in the computational basis for qubit number 3:

In[59]:=

hamiltonian = ResourceFunction[
"QuantumHamiltonianOperator"][{"LinearInterpolation", {{1, 0}, {0, 0}} -> {{1/2, 1/2}, {-1/2, 1/2}}}, {3}];
hamiltonian["Operator"]

Out[59]=

Represent the same linear interpolation between QuantumHamiltonianOperator objects directly (for qubit number 3):

In[60]:=

(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/e81aa49f-d47f-420d-a1db-873b74b77f2e"]

Out[60]=

Represent a linear interpolation between two Hamiltonian matrices in the computational basis for qubit number 3, with evolution parameter y ranging from -2 to 2 in steps of 1/20:

In[61]:=

$hamiltonian3 = ResourceFunction[ "QuantumHamiltonianOperator"][{"LinearInterpolation", {{1, 0}, {0, 0}} -> {{1/2, 1/2}, {-1/2, 1/2}}, \[FormalY], -2, 2, 1/20}]; hamiltonian3["Operator"]$

Out[61]=

In[62]:=

Out[62]=

Represent a linear interpolation between two associated evolution operators (i.e. two associated solutions to the Schrödinger equation), represented as QuantumDiscreteOperator objects, for qubit 3:

In[63]:=

hamiltonian4 = ResourceFunction[
"QuantumHamiltonianOperator"][{"LinearInterpolation", ResourceFunction["QuantumDiscreteOperator"]["PauliX", {3}] -> ResourceFunction["QuantumDiscreteOperator"]["PauliY", {3}]}];
hamiltonian4["Operator"]

Out[63]=

Use a shorthand to represent the same linear interpolation between Hamiltonian matrices as above:

In[64]:=

Out[64]=

Use a shorthand to represent the same linear interpolation between QuantumHamiltonianOperator objects as above:

In[65]:=

(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/6be6350f-e5d2-4df4-84a2-e2ddbd5fd861"]

Out[65]=

Use a shorthand to represent the same linear interpolation between associated evolution operators (i.e. associated solutions to the Schrödinger equation), represented as QuantumDiscreteOperator objects, as above:

In[66]:=

hamiltonian7 = ResourceFunction["QuantumHamiltonianOperator"][
ResourceFunction["QuantumDiscreteOperator"]["PauliX", {3}] -> ResourceFunction["QuantumDiscreteOperator"]["PauliY", {3}]];
hamiltonian7["Operator"]

Out[66]=

Represent a Hamiltonian operator with a specified associated evolution operator (i.e. associated solution to the Schrödinger equation) represented as a QuantumDiscreteOperator object, for qubit number 2:

In[67]:=

$hamiltonian = ResourceFunction[ "QuantumHamiltonianOperator"][{"EvolutionOperator", ResourceFunction[ "QuantumDiscreteOperator"][{{1 - Exp[\[FormalT]^2], 1 + Exp[\[FormalT]^2]}, {Exp[\[FormalT]^3], 1 + Exp[\[FormalT]^2]}}, {2}]}]; hamiltonian["Operator"]$

Out[67]=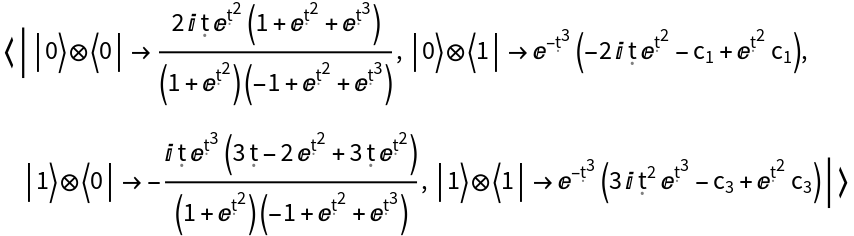

Represent a Hamiltonian operator with a specified associated evolution operator (i.e. associated solution to the Schrödinger equation) represented in pure matrix form, for qubit number 2:

In[68]:=

$hamiltonian2 = ResourceFunction[ "QuantumHamiltonianOperator"][{"EvolutionOperator", {{1 - Exp[\[FormalT]^2], 1 + Exp[\[FormalT]^2]}, {Exp[\[FormalT]^3], 1 + Exp[\[FormalT]^2]}}}, {2}]; hamiltonian2["Operator"]$

Out[68]=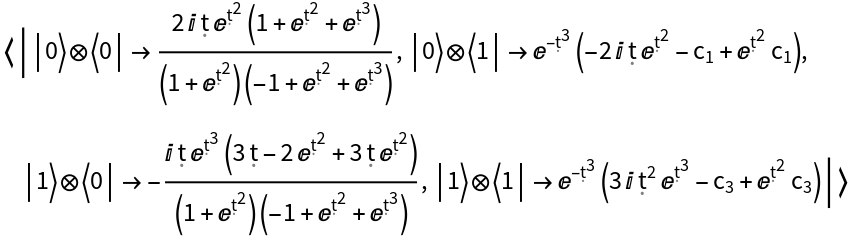

Represent a Hamiltonian operator with a specified associated evolution operator (i.e. associated solution to the Schrödinger equation) for qubit number 2, with evolution parameter x ranging from -1 to 1 in steps of 1/10:

In[69]:=

$hamiltonian3 = ResourceFunction[ "QuantumHamiltonianOperator"][{"EvolutionOperator", ResourceFunction[ "QuantumDiscreteOperator"][{{1 - Exp[\[FormalX]^2], 1 + Exp[\[FormalX]^2]}, {Exp[\[FormalX]^3], 1 + Exp[\[FormalX]^2]}}, {2}], \[FormalX], -1, 1, 1/10}]; hamiltonian3["Operator"]$

Out[69]=

In[70]:=

Out[70]=

Use a shorthand to represent the same Hamiltonian operator with specified associated evolution operator (i.e. associated solution to the Schrödinger equation) represented as a QuantumDiscreteOperator, as above:

In[71]:=

$hamiltonian4 = ResourceFunction["QuantumHamiltonianOperator"][ ResourceFunction[ "QuantumDiscreteOperator"][{{1 - Exp[\[FormalT]^2], 1 + Exp[\[FormalT]^2]}, {Exp[\[FormalT]^3], 1 + Exp[\[FormalT]^2]}}, {2}]]; hamiltonian4["Operator"]$

Out[71]=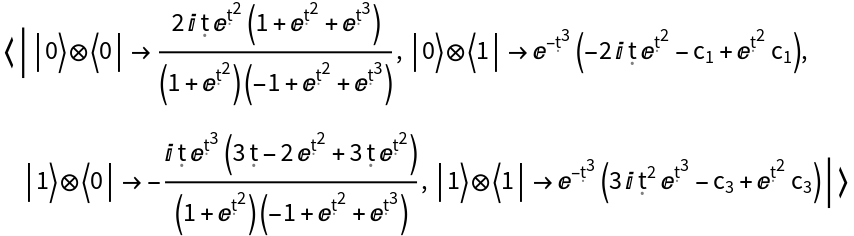

View a list of properties that can be extracted from a QuantumHamiltonianOperator object:

In[72]:=

Out[72]=

In[73]:=

Out[73]=

Return the operator association:

In[74]:=

Out[74]=

Return which QuantumBasis the Hamiltonian operator is defined with respect to:

In[75]:=

Out[75]=

Return which quantum mechanical picture the Hamiltonian operator is defined with respect to:

In[76]:=

Out[76]=

Return the association of names and basis elements:

In[77]:=

Out[77]=

Return the evolution parameter:

In[78]:=

Out[78]=

Return the initial and final values of the evolution parameter:

In[79]:=

Out[79]=

Return the step size for the evolution parameter:

In[80]:=

Out[80]=

Return the matrix representation (including explicit dependence upon the evolution parameter):

In[81]:=

Out[81]=

Return the matrix representation with the evolution parameter set to 0.4:

In[82]:=

Out[82]=

Return the initial and final matrix representations (i.e. matrix representations with the evolution parameter set to its initial and final values, respectively):

In[83]:=

Out[83]=

In[84]:=

Out[84]=

Return the ordered matrix representation (when applied to qubit 2) assuming a state consisting of 2 qubits, including explicit dependence upon the evolution parameter:

In[85]:=

Out[85]=

Return the ordered matrix representation (when applied to qubit 2) assuming a state consisting of 3 qubits, including explicit dependence upon the evolution parameter:

In[86]:=

Out[86]=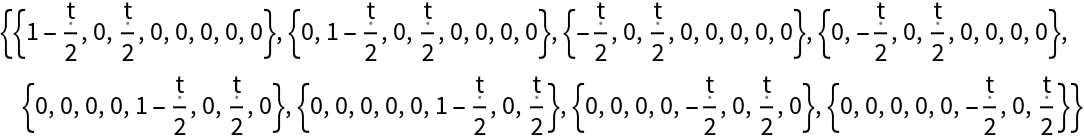

Return the ordered matrix representation (when applied to qubit 2) assuming a state consisting of 3 qubits, with the evolution parameter set to 0.4:

In[87]:=

Out[87]=

Return the initial and final ordered matrix representations (i.e. matrix representations with the evolution parameter set to its initial and final values, respectively) when applied to qubit 2, assuming a state consisting of 2 qubits:

In[88]:=

Out[88]=

In[89]:=

Out[89]=

In[90]:=

Out[90]=

In[91]:=

Out[91]=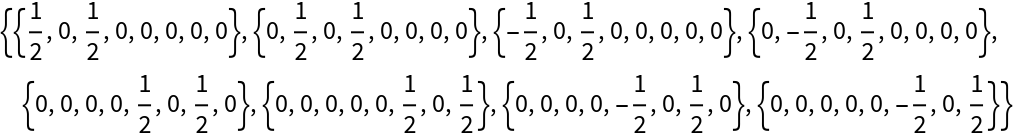

Return the arity (number of input subsystems):

In[92]:=

Out[92]=

Return the number of dimensions:

In[93]:=

Out[93]=

Return the order in which the Hamiltonian operator is applied to subsystems:

In[94]:=

Out[94]=

Determine whether the Hamiltonian operator is Hermitian:

In[95]:=

Out[95]=

Determine whether the Hamiltonian operator is unitary:

In[96]:=

Out[96]=

Return the list of eigenvalues:

In[97]:=

Out[97]=

Return the list of eigenvectors:

In[98]:=

Out[98]=

Return the minimum value of the gap between the two eigenvalues (and the value of the evolution parameter for which the minimum gap occurs):

In[99]:=

Out[99]=

Return the initial and final values of the gap between the first two eigenvalues (i.e. gaps with the evolution parameter set to its initial and final values, respectively):

In[100]:=

Out[100]=

Return the list of gaps between the first two eigenvalues (for all intermediate values of the evolution parameter):

In[101]:=

Out[101]=

Return the value of the gap between the first two eigenvalues, with the evolution parameter set to 0.4:

In[102]:=

Out[102]=

Return the corresponding evolution operator (i.e. the corresponding solution to the Schrödinger equation), including explicit dependence upon the evolution parameter:

In[103]:=

Out[103]=

In[104]:=

Out[104]=

Return the corresponding evolution operator (i.e. the corresponding solution to the Schrödinger equation), with the evolution parameter set to 0.4:

In[105]:=

Out[105]=

In[106]:=

Out[106]=

Return the initial and final evolution operators (i.e. the corresponding solutions to the Schrödinger equation, with the evolution parameter set to its initial and final values, respectively):

In[107]:=