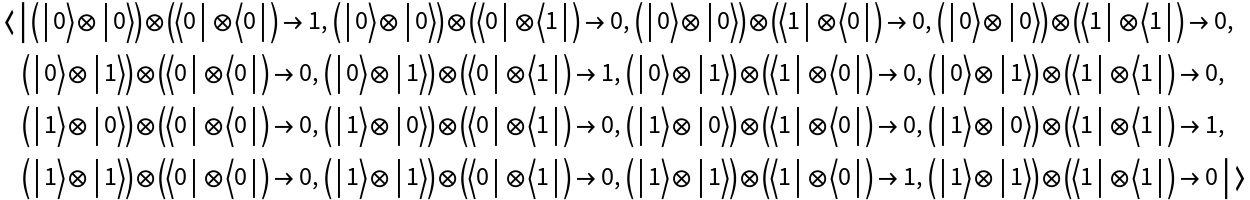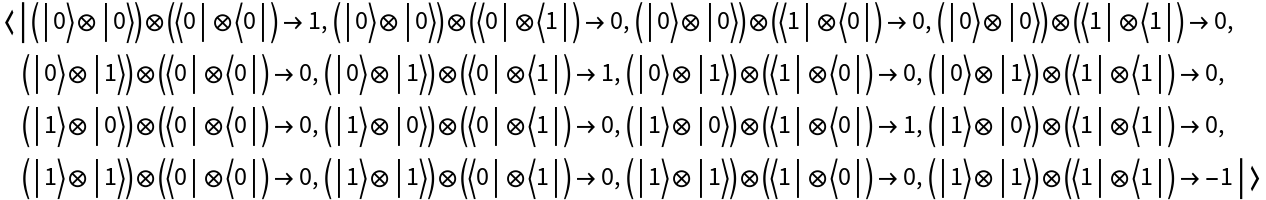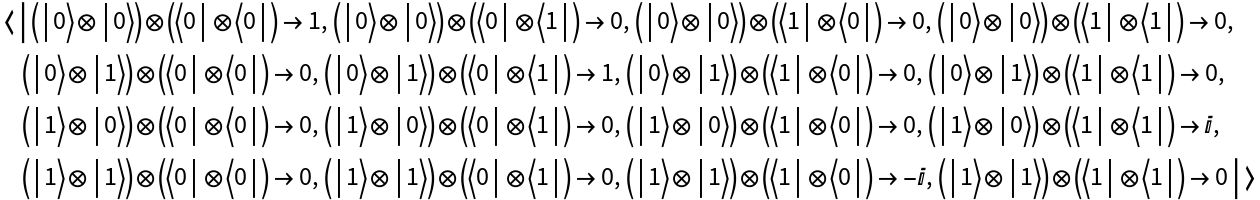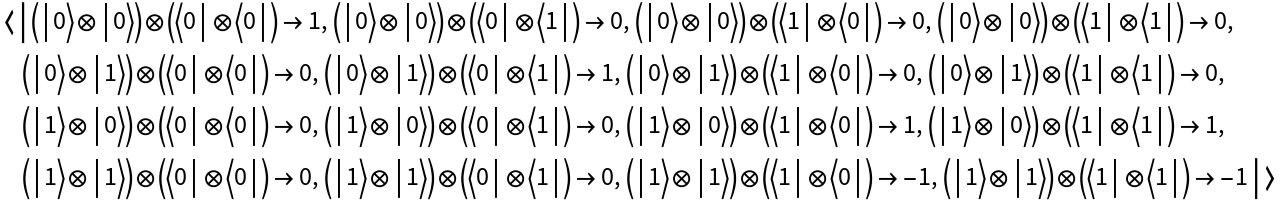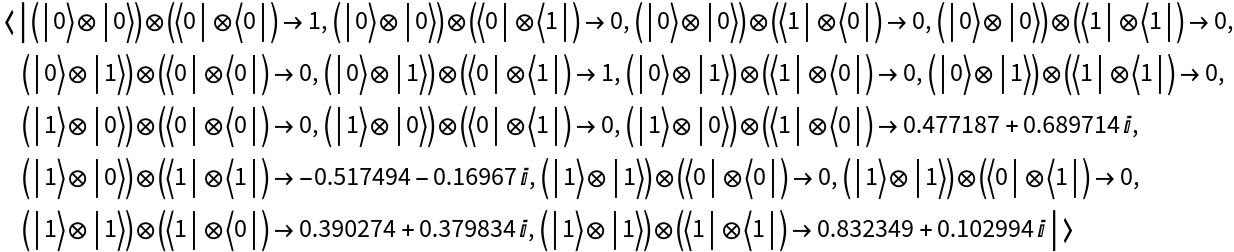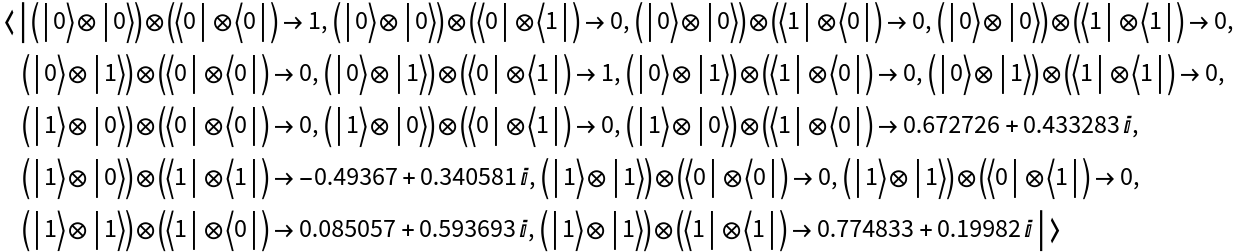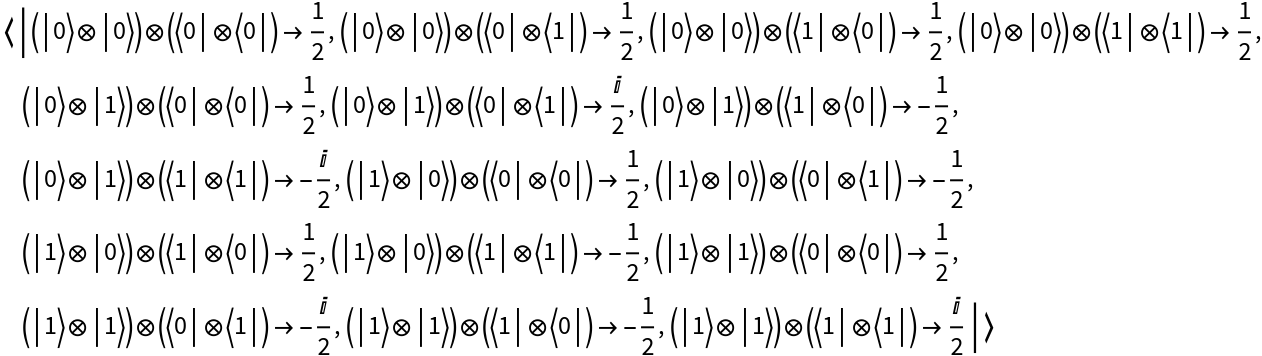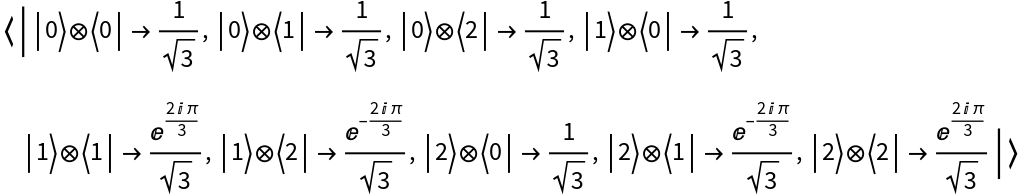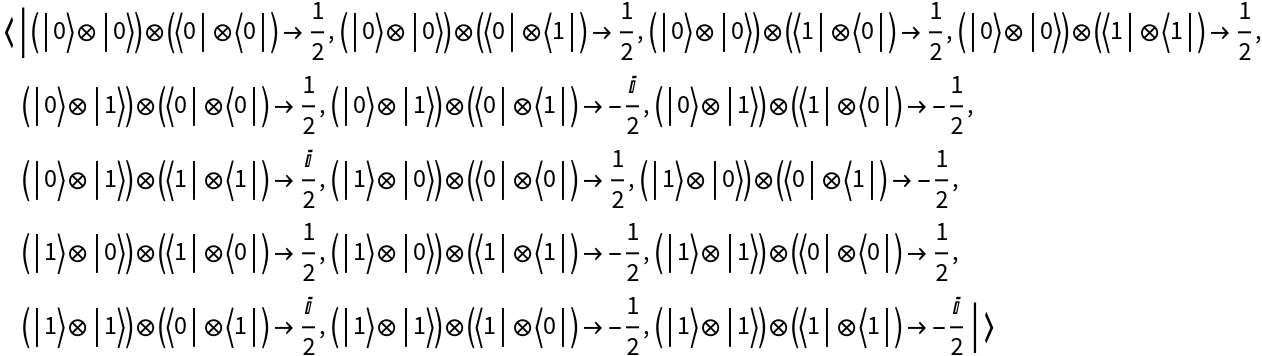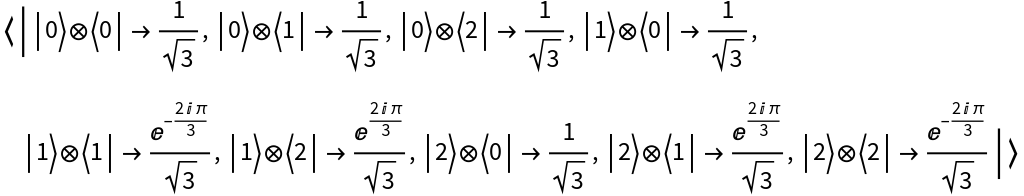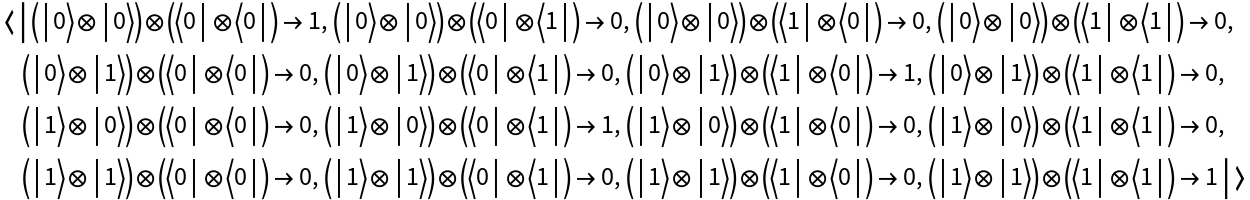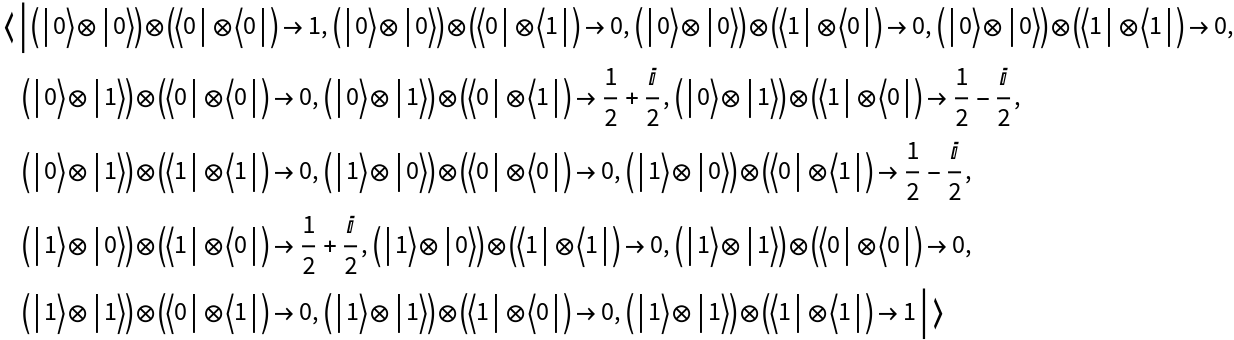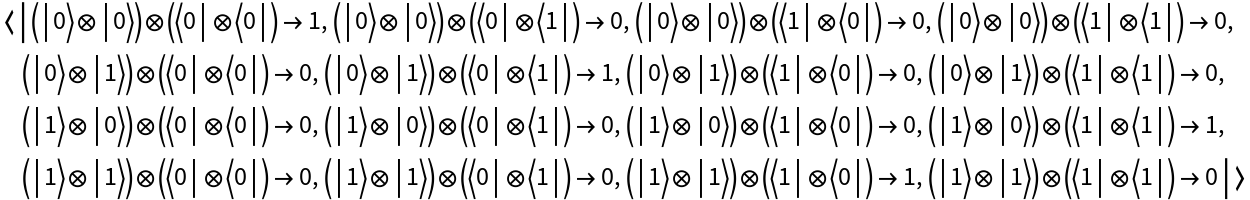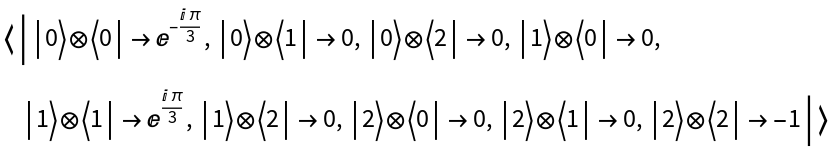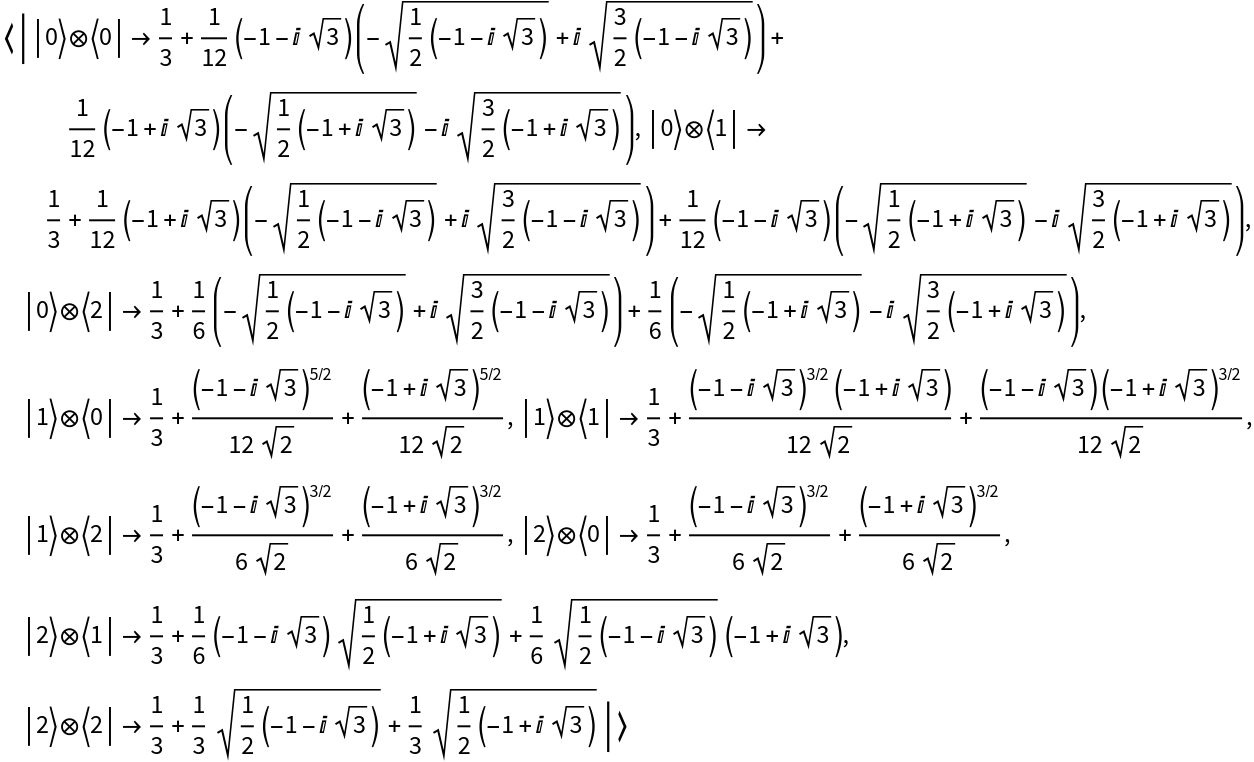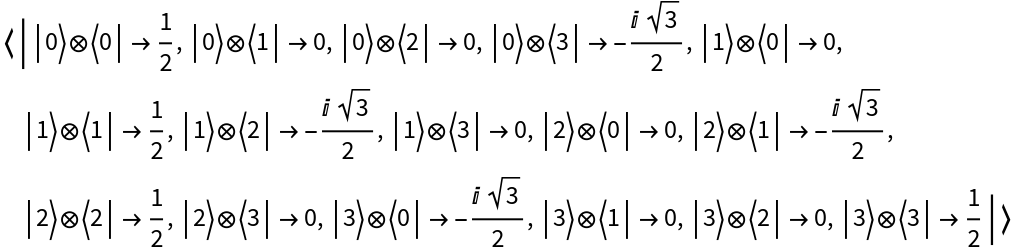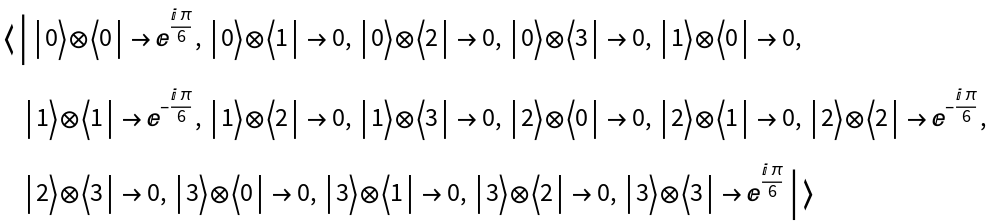Basic Examples (7)
Create a discrete quantum operator from a matrix representation in the computational basis (default):
Return its operator association:
Apply the operator to the first qubit (default) of a two-qubit discrete quantum state in the computational basis:
Apply the operator instead to the second qubit of the state:
Create a discrete quantum operator from a matrix representation in a specified basis (Pauli-X) and return its matrix representation:
Return its operator association:
Show that the operator is unitary, but not Hermitian:
Return the ordered matrix representation (assuming a state of size 2):
Return the ordered matrix representation (assuming a state size of 3):
Return the ordered matrix representation (assuming a state of size 2) assuming that the operator is applied instead to the second qubit of the state:
Create a discrete quantum operator by explicitly specifying an association of matrix elements in a given (tensor product) basis and return its matrix representation:
Return its basis element association:
Return its operator association:
Create a CNOT gate for qubits (default), with the third qubit being the control and the fourth qubit being "active":
Create a CNOT gate for 3-dimensional qudits, with the second qudit being the control and the first qudit being "active":
Create an XX Ising coupling gate with rotation angle π/3, applied to qubits 5 and 2:
By default, all discrete quantum operators are created in the Schrodinger picture:
Operators in the Schrodinger picture can be applied to QuantumDiscreteState objects:
However, they cannot be applied to other operators (i.e. QuantumDiscreteOperator objects, QuantumMeasurementOperator objects, QuantumHamiltonianOperator objects or QuantumCircuitOperator objects). Doing so will return unevaluated:
On the other hand, operators created in the Heisenberg picture cannot be applied to QuantumDiscreteState objects (will return unevaluated):
However, they can be applied to other operators in the Heisenberg picture (i.e. QuantumDiscreteOperator objects, QuantumMeasurementOperator objects, QuantumHamiltonianOperator objects or QuantumCircuitOperator objects):
By default, all discrete quantum operators are assumed to apply to tensor products of 2-dimensional subsystems (i.e. qubits):
Create a discrete quantum operator with the same matrix representation applying to a single 4-dimensional subsystem (i.e. qudit) instead:
Create a discrete quantum operator in the computational basis (default):
Transform the operator to the Fourier basis:
Transform the operator back to the computational basis:
The initial and final operators are the same:
Scope (21)
Represent the RootSWAP gate in the Heisenberg picture:
Transform the operator to the interaction picture:
Represent a 2-qubit random unitary operator in the computational basis:
Represent the same operator in the Pauli-X basis instead:
Operators in the Schrodinger picture can be applied to QuantumDiscreteState objects that are also in the Schrodinger picture:
However, they cannot be applied to other operators in the Schrodinger picture (returns unevaluated):
Likewise, operators in the "PhaseSpace" picture can be applied to QuantumDiscreteState objects in the "PhaseSpace" picture:
But they cannot be applied to other operators in the phase space picture (returns unevaluated):
On the other hand, operators in the Heisenberg picture cannot be applied to QuantumDiscreteState objects in the Heisenberg picture:
But they can be applied to other operators in the Heisenberg picture:
Finally, operators in the Interaction picture can be applied to both QuantumDiscreteState objects in the Interaction picture:
And also to other operators in the Interaction picture:
In general, the quantum mechanical pictures of a QuantumDiscreteOperator and the object that it is being applied to must match.
Represent a rotation gate for qubit number 3 with angle π/3 around the x axis of the Bloch sphere:
Represent a rotation gate for qubit number 3 with angle π/3 around the y axis of the Bloch sphere:
Represent a rotation gate for qubit number 3 with angle π/3 around the z axis of the Bloch sphere:
Represent an S-gate (a π/2 phase change gate) for qubit number 2:
Represent a T-gate (a π/4 phase change gate) for qubit number 2:
Represent a CNOT gate (a controlled NOT gate) on qubits for control qubit 2 and "active" qubit 3:
Represent a CNOT gate (a controlled NOT gate) on 3-dimensional qudits for control qudit 2 and "active" qudit 3:
Represent a CPHASE gate (a controlled π phase change gate) on qubits for control qubit 3 and "active" qubit 4:
Represent a CPHASE gate (a controlled π phase change gate) on 3-dimensional qudits for control qudit 3 and "active" qudit 4:
Represent a CX gate (a controlled Pauli-X gate—equivalent to a CNOT) on qubits for control qubit 1 and "active" qubit 2:
Represent a CX gate (a controlled Pauli-X gate - equivalent to a CNOT) on 3-dimensional qudits for control qudit 1 and "active" qudit 2:
Represent a CY gate (a controlled Pauli-Y gate) for control qubit 1 and "active" qubit 2:
Represent a CZ gate (a controlled Pauli-Z gate) on qubits for control qubit 1 and "active" qubit 2:
Represent a CZ gate (a controlled Pauli-Z gate) on 3-dimensional qudits for control qudit 1 and "active" qudit 2:
Represent a controlled-U gate (with U being a random 2-by-2 unitary matrix) on qubits for control qubit 2 and "active" qubit 3 and 2:
Represent a controlled-U gate (with U being a random 3-by-3 unitary matrix) on 3-dimensional qudits for control qudit 2 and "active" qudit 3:
Construct a controlled-U gate on qubits (with the same 2-by-2 matrix as before), for controlled qubit 2 and "active" qubit 3, directly using the operator form of the matrix:
Construct a controlled-U gate on 3-dimensional qudits (with the same 3-by-3 matrix as before), for controlled qudit 2 and "active" qudit 3, directly using the operator form of the matrix:
Represent a single-qubit QFT gate (quantum Fourier transform) for qubit number 3:
Represent a two-qubit QFT gate (quantum Fourier transform) for qubits 3 and 4:
Represent a single-qudit QFT gate (quantum Fourier transform) on 3-dimensional qudits for qudit number 3:
Represent a two-qudit QFT gate (quantum Fourier transform) on 3-dimensional qudits for qudits 3 and 4:
Represent a single-qubit IQFT gate (inverse quantum Fourier transform) for qubit number 3:
Represent a two-qubit IQFT gate (inverse quantum Fourier transform) for qubits 3 and 4:
Represent a single-qudit IQFT gate (inverse quantum Fourier transform) on 3-dimensional qudits for qudit number 3:
Represent a two-qudit IQFT gate (inverse quantum Fourier transform) on 3-dimensional qudits for qudits 3 and 4:
Represent a SWAP gate on qubits (swaps two qubits) for qubits 1 and 2:
Represent a SWAP gate on 3-dimensional qudits (swaps two qudits) for qudits 1 and 2:
Represent the square root of a SWAP gate on qubits (half swaps two qubits) for qubits 1 and 2:
Represent the square root of a SWAP gate on 3-dimensional qudits (half swaps two qudits) for qudits 1 and 2:
Represent a SUM gate on qubits (a half-adder for qubits—similar to a CNOT gate) for qubits 2 and 3:
Represent a SUM gate on 3-dimensional qudits (a half-adder for qudits—similar to a CNOT gate) for qudits 2 and 3:
Represent a Pauli-X gate (a π rotation around the x axis of the Bloch sphere) on qubits for qubit number 3:
Represent a Pauli-X gate on 3-dimensional qudits for qudit number 3:
Represent a Pauli-Y gate (a π rotation around the y axis of the Bloch sphere) on qubits for qubit number 3:
Represent a Pauli-Z gate (a π rotation around the z axis of the Bloch sphere) on qubits for qubit number 3:
Represent a Pauli-Z gate on 3-dimensional qudits for qudit number 3:
Represent the square root of a NOT gate on qubits (half a Pauli-X rotation) for qubit number 3:
Represent the square root of a NOT gate on 3-dimensional qudits (half a Pauli-X rotation) for qudit number 3:
Represent a Hadamard gate (a single-qubit quantum Fourier transform) for qubit number 1:
Represent a Toffoli gate (a π/2 Deutsch gate) on 3 qubits for qubits 2, 3 and 4:
Represent a Toffoli gate on 4 qubits for qubits 2, 3, 4 and 5:
Represent a CSWAP (controlled SWAP gate, otherwise known as a Fredkin gate) for qubits 3, 4 and 5:
Represent an XX gate for qubit 4 (an x axis Ising coupling gate) with angle π/3:
Represent a YY gate for qubit 4 (a y axis Ising coupling gate) with angle π/3:
Represent a ZZ gate for qubit 4 (a z axis Ising coupling gate) with angle π/3:
Represent a Deutsch gate for qubits 1, 2 and 3 with phase π/3:
Represent a single-qubit random unitary operator (selected from a Gaussian unitary ensemble) for qubit 2:
Represent a two-qubit random unitary operator (selected from a Gaussian unitary ensemble) for qubits 2 and 3:
Represent a single-qudit random unitary operator (selected from a Gaussian unitary ensemble) on 3-dimensional qudits for qudit 2:
Represent a two-qudit random unitary operator (selected from a Gaussian unitary ensemble) on 3-dimensional qudits for qudits 2 and 3:
QuantumDiscreteOperator objects can be constructed purely symbolically (without explicit matrix elements):
View the operator association:
Standard operations can still be performed on purely symbolic operators/states:
View a list of properties that can be extracted from a QuantumDiscreteOperator object:
Return the operator association:
Return which QuantumBasis the operator is defined with respect to:
Return which quantum mechanical picture the operator is defined with respect to:
Return the association of names and basis elements:
Return the matrix representation:
Return the ordered matrix representation (when applied to qubits 2 and 3) assuming a state consisting of 3 qubits:
Return the ordered matrix representation (when applied to qubits 2 and 3) assuming a state consisting of 4 qubits:
Return the arity (number of input subsystems):
Return the number of dimensions:
Return the order in which the operator is applied to subsystems:
Determine whether the operator is Hermitian:
Determine whether the operator is unitary:
Return the list of eigenvalues:
Return the list of eigenvectors:
![operator = ResourceFunction[
"QuantumDiscreteOperator"][{{(1 + I)/2, (I - 1)/2}, {(I - 1)/
2, (1 + I)/2}}, ResourceFunction["QuantumBasis"]["PauliX"]];
operator["MatrixRepresentation"]](https://www.wolframcloud.com/obj/resourcesystem/images/fc6/fc644ba7-7dc3-46a2-b763-23ec76b16a56/00d29075b5fad2d8.png)
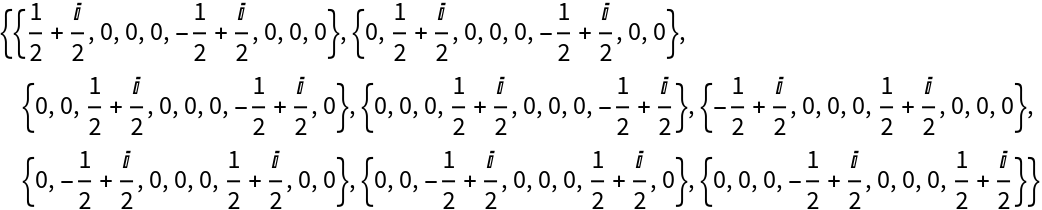
![operator = ResourceFunction[
"QuantumDiscreteOperator"][<|TensorProduct[Ket[0], Ket[0]] -> I, TensorProduct[Ket[0], Ket[1]] -> -1, TensorProduct[Ket[1], Ket[0]] -> -I, TensorProduct[Ket[1], Ket[1]] -> 1|>, {1}];
operator["MatrixRepresentation"]](https://www.wolframcloud.com/obj/resourcesystem/images/fc6/fc644ba7-7dc3-46a2-b763-23ec76b16a56/0f341f5261c557a1.png)
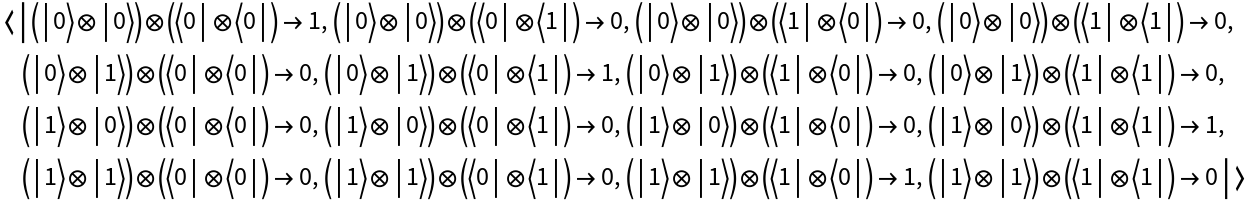

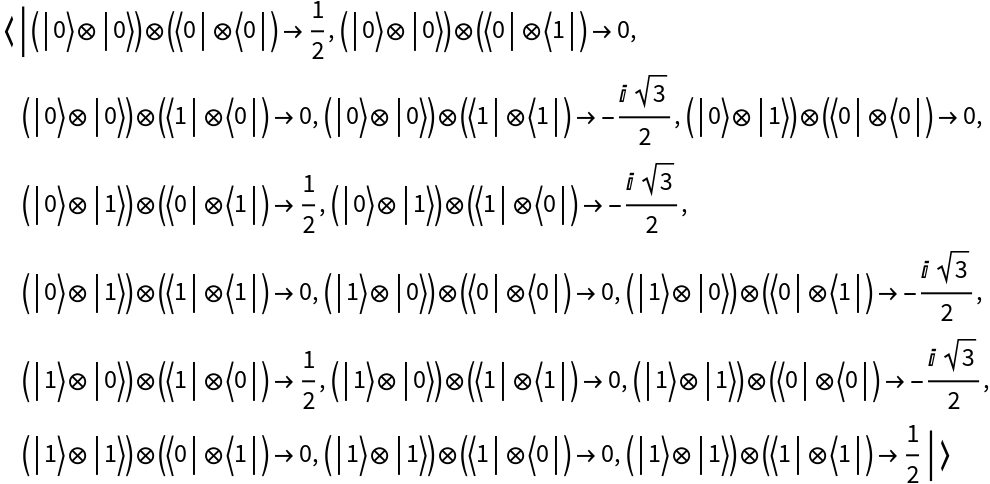

![measurement = ResourceFunction["QuantumMeasurementOperator"]["RandomHermitian", "Heisenberg"];
operator3[measurement]](https://www.wolframcloud.com/obj/resourcesystem/images/fc6/fc644ba7-7dc3-46a2-b763-23ec76b16a56/7c6d11ab1a41da67.png)
![hamiltonian = ResourceFunction["QuantumHamiltonianOperator"]["RandomHermitian", "Heisenberg"];
operator3[hamiltonian]](https://www.wolframcloud.com/obj/resourcesystem/images/fc6/fc644ba7-7dc3-46a2-b763-23ec76b16a56/19e2e0e9fb74f540.png)
![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["RandomUnitary", "Heisenberg"]}, "Heisenberg"];
operator3[circuit]](https://www.wolframcloud.com/obj/resourcesystem/images/fc6/fc644ba7-7dc3-46a2-b763-23ec76b16a56/5e0b55983dca32ff.png)
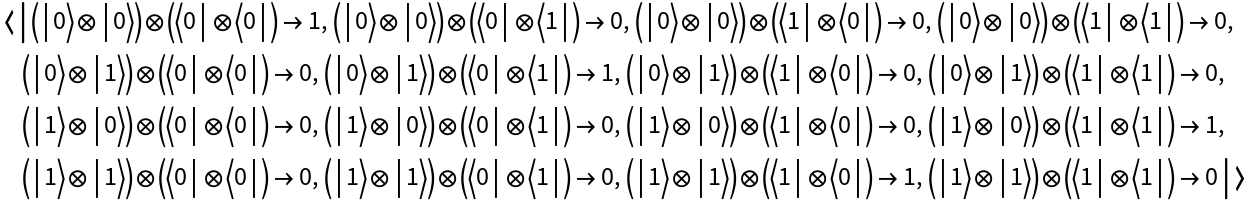
![operator2 = ResourceFunction["QuantumDiscreteOperator"][operator, ResourceFunction["QuantumBasis"]["Fourier"]];
operator2["Operator"]](https://www.wolframcloud.com/obj/resourcesystem/images/fc6/fc644ba7-7dc3-46a2-b763-23ec76b16a56/6b92b140ee96c5f6.png)
![operator3 = ResourceFunction["QuantumDiscreteOperator"][operator2, ResourceFunction["QuantumBasis"]["Computational"]];
operator3["Operator"]](https://www.wolframcloud.com/obj/resourcesystem/images/fc6/fc644ba7-7dc3-46a2-b763-23ec76b16a56/6a26cd16923e0f47.png)

![operator2 = ResourceFunction["QuantumDiscreteOperator"][operator, ResourceFunction["QuantumBasis"]["PauliX", 2]];
operator2["Operator"]](https://www.wolframcloud.com/obj/resourcesystem/images/fc6/fc644ba7-7dc3-46a2-b763-23ec76b16a56/56a32bc55fa009aa.png)