Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Represent a discrete quantum measurement operator
ResourceFunction["QuantumMeasurementOperator"][<|b11→e11,b12→e12,…|>,order,QuantumBasis[…]] represents a discrete projection-valued quantum measurement operator with (tensor products of) basis elements bij and associated matrix elements eij, applied to qudits indexed by order, defined with respect to a specified QuantumBasis. | |
ResourceFunction["QuantumMeasurementOperator"][<|b1→o1,b2→o2,…|>,order,QuantumBasis[…]] represents a discrete positive operator-valued quantum measurement operator with basis elements bi and associated matrix operators oi, applied to qudits indexed by order, defined with respect to a specified QuantumBasis. | |
ResourceFunction["QuantumMeasurementOperator"][mat,order,QuantumBasis[…]] represents a discrete projection-valued quantum measurement operator with matrix representation mat, applied to the qudits indexed by order, defined with respect to a specified QuantumBasis. | |
ResourceFunction["QuantumMeasurementOperator"][ops,order,QuantumBasis[…]] represents a discrete positive operator-valued quantum measurement operator with the list of matrix operators ops, applied to the qudits indexed by order, defined with respect to a specified QuantumBasis. | |
ResourceFunction["QuantumMeasurementOperator"][{QuantumBasis[…],eigs},order] represents a discrete projection-valued quantum measurement operator with respect to the specified QuantumBasis, with possible outcomes/eigenvalues given by the list eigs, applied to the qudits indexed by order. | |
ResourceFunction["QuantumMeasurementOperator"]["name",order,pic] represents a named discrete projection-valued quantum measurement operator "name", applied to the qudits indexed by order, with respect to the quantum mechanical picture pic. | |
ResourceFunction["QuantumMeasurementOperator"][{"name",d},order,pic] represents a d-dimensional version of a named discrete projection-valued quantum measurement operator "name", applied to the qudits indexed by order, with respect to the quantum mechanical picture pic. | |
ResourceFunction["QuantumMeasurementOperator"][{"name",d,eigs},order,pic] represents a discrete projection-valued quantum measurement operator with respect to a named basis "name", with possible outcomes/eigenvalues given by the list eigs, applied to the qudits indexed by order, with respect to the quantum mechanical picture pic. | |
ResourceFunction["QuantumMeasurementOperator"][ResourceFunction["QuantumMeasurementOperator"][…],QuantumBasis[…]] transforms a specified ResourceFunction["QuantumMeasurementOperator"] into a new QuantumBasis. | |
ResourceFunction["QuantumMeasurementOperator"][ResourceFunction["QuantumMeasurementOperator"][…],pic] transforms a specified ResourceFunction["QuantumMeasurementOperator"] into the new quantum mechanical picture pic. |
| "Operator" | association <|b11→e11,b12→e12,…|> of tensor products of basis names and matrix elements (for projection-valued measurements), or association <|b1→o1,b2→o2,…|> of basis names and matrix operators (for positive operator-valued measurements) |
| "Basis" | which QuantumBasis the measurement operator is defined with respect to |
| "Picture" | which quantum mechanical picture the measurement operator is defined with respect to |
| "BasisElements" | list of basis elements bi |
| "MatrixRepresentation" | matrix representation mat of the measurement operator (projection-valued measurements only) |
| "POVMElements" | list of operator matrices ops of the measurement operator (positive operator-valued measurements only) |
| "OrderedMatrixRepresentation" | matrix representation adjusted according to the order of the measurement operator, assuming an input state containing Max[order] qudits (subsystems) |
| {"OrderedMatrixRepresentation",n} | matrix representation adjusted according to the order of the measurement operator, assuming an input state containing n qudits (subsystems) |
| "OrderedPOVMElements" | list of operator matrices adjusted according to the order of the measurement operator, assuming an input state containing Max[order] qudits (subsystems) |
| {"OrderedPOVMElements",n} | list of operator matries adjusted according to the order of the measurement operator, assuming an input state containing n qudits (subsystems) |
| "Arity" | arity of the measurement operator |
| "Dimensions" | dimensionality of each qudit (subsystem) in the input state for the measurement operator |
| "Order" | order in which the measurement operator should be applied to qudits (subsystems) in the input state |
| "HermitianQ" | whether the operator is Hermitian (self-adjoint) |
| "UnitaryQ" | whether the operator is unitary (an automorphism of Hilbert space) |
| "Eigenvalues" | eigenvalues of the matrix representation(s) of the measurement operator |
| "Eigenvectors" | eigenvectors of the matrix representation(s) of the measurement operator |
| "ProjectionQ" | whether the measurement operator is projection-valued |
| "POVMQ" | whether the measurement operator is positive operator-valued |
| "Properties" | list of all property names |
| "PauliX" | measurement operator based on the Pauli-X gate for qubits (equivalent to a π rotation around the x-axis of the Bloch sphere) |
| {"PauliX",d} | measurement operator based on the Pauli-X gate for d-dimensional qudits (not Hermitian for general d>2) |
| "PauliY" | measurement operator based on the Pauli-Y gate for qubits (equivalent to a π rotation around the y axis of the Bloch sphere) |
| "PauliZ" | measurement operator based on the Pauli-Z gate for qubits (equivalent to a π rotation around the z axis of the Bloch sphere) |
| {"PauliZ",d} | measurement operator based on the Pauli-Z gate for d-dimensional qudits (not Hermitian for general d>2) |
| "Hadamard" | measurement operator based on the Hadamard gate for qubits (equivalent to a QFT gate on one qubit) |
| "RandomHermitian" | random Hermitian operator on qubits (Gaussian Hermitian ensemble) |
| {"RandomHermitian",d} | random Hermitian operator for d-dimensional qudits |
| "ComputationalBasis" | measurement in the 2-dimensional computational basis |
| {"ComputationalBasis",d} | measurement in the d-dimensional computational basis |
| {"ComputationalBasis",d,eigs} | measurement in the d-dimensional computational basis with eigenvalues (i.e. measurement outcomes) eigs |
| "BellBasis" | measurement in the Bell basis |
| {"BellBasis",eigs} | measurement in the Bell basis with eigenvalues (i.e. measurement outcomes) eigs |
| "PauliBasis" | measurement in the basis of Pauli matrices |
| {"PauliBasis",eigs} | measurement in the basis of Pauli matrices with eigenvalues (i.e. measurement outcomes) eigs |
| "FourierBasis" | measurement in the 2-dimensional basis of the quantum Fourier transform |
| {"FourierBasis",d} | measurement in the d-dimensional basis of the quantum Fourier transform |
| {"FourierBasis",d,eigs} | measurement in the d-dimensional basis of the quantum Fourier transform with eigenvalues (i.e. measurement outcomes) eigs |
Create a projection-valued discrete quantum measurement operator from a matrix representation in the computational basis (default):
| In[1]:= |
| Out[1]= |
Return its operator association:
| In[2]:= |
| Out[2]= |
Apply the measurement operator to the first qubit (default) of a two-qubit discrete quantum state in the computational basis:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= |
Apply the measurement operator instead to the second qubit of the state:
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |
Create a positive operator-valued discrete quantum measurement operator from a list of matrix representations in the computational basis (default):
| In[7]:= | ![o1 = {{0, 0}, {0, Sqrt[2]/(1 + Sqrt[2])}};
o2 = (Sqrt[2]/(2 + 2 Sqrt[2]))*{{1, -1}, {-1, 1}};
o3 = IdentityMatrix[2] - o1 - o2;
measurement = ResourceFunction["QuantumMeasurementOperator"][{o1, o2, o3}]](https://www.wolframcloud.com/obj/resourcesystem/images/b11/b11252e7-529e-4cc9-bbd6-fc2482e889d4/233ab0c58f1c8ff3.png) |
| Out[7]= |
Show that the measurement operator is positive operator-valued:
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |
Return its list of operator matrices:
| In[10]:= |
| Out[10]= | 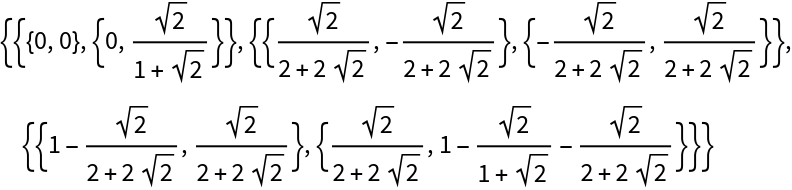 |
Return the ordered list of operator matrices (assuming a state of size 2):
| In[11]:= |
| Out[11]= | 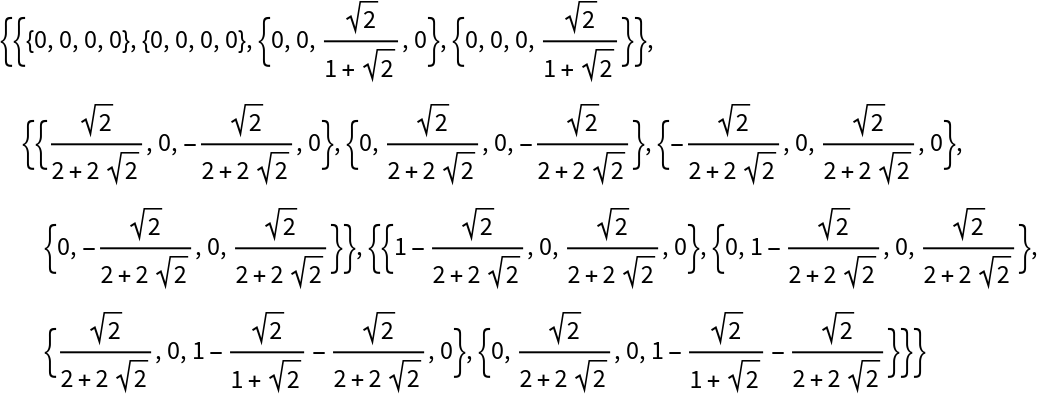 |
Return the ordered list of operator matrices (assuming a state of size 3):
| In[12]:= |
| Out[12]= | 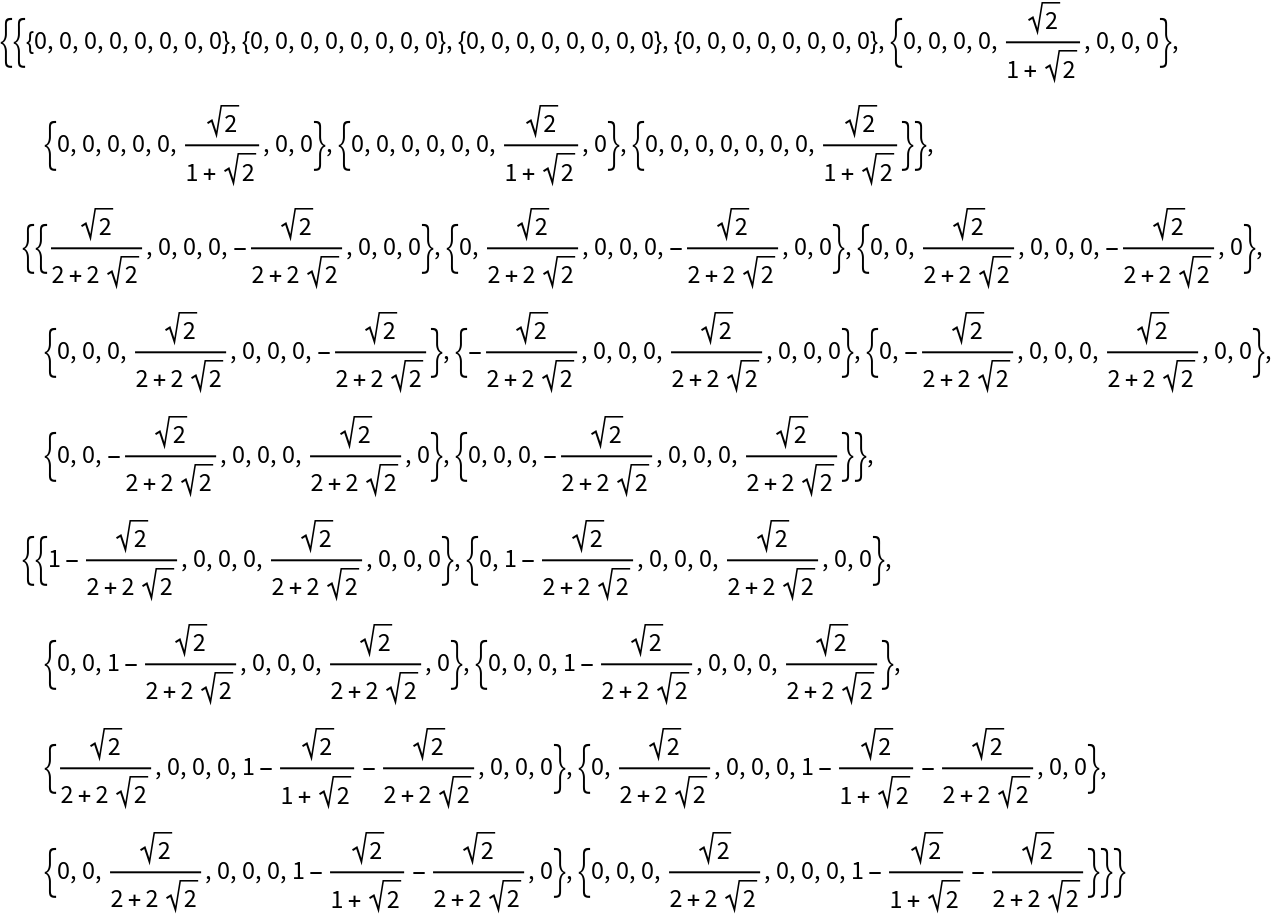 |
Return its operator association:
| In[13]:= |
| Out[13]= | 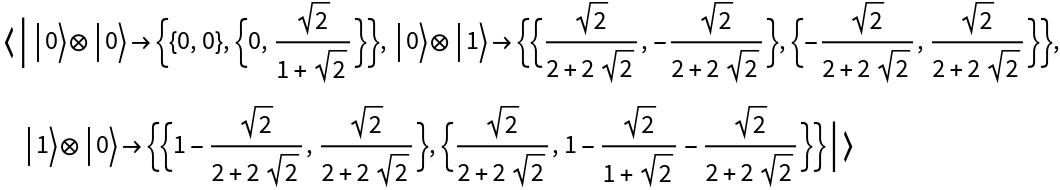 |
Apply the measurement operator to the first qubit (default) of a two-qubit discrete quantum state in the computational basis:
| In[14]:= |
| Out[14]= |
Create a projection-valued discrete quantum measurement operator from a matrix representation in a specified basis (Pauli-X) and return its matrix representation:
| In[15]:= | ![measurement = ResourceFunction[
"QuantumMeasurementOperator"][{{1/2, -1/2}, {-1/2, 1/2}}, ResourceFunction["QuantumBasis"]["PauliX"]];
measurement["MatrixRepresentation"]](https://www.wolframcloud.com/obj/resourcesystem/images/b11/b11252e7-529e-4cc9-bbd6-fc2482e889d4/09310c0f609c2e7c.png) |
| Out[15]= |
Return its operator association:
| In[16]:= |
| Out[16]= |
Show that the measurement operator is Hermitian, but not unitary:
| In[17]:= |
| Out[17]= |
| In[18]:= |
| Out[18]= |
Return the ordered matrix representation (assuming a state of size 2):
| In[19]:= |
| Out[19]= |
Return the ordered matrix representation (assuming a state of size 3):
| In[20]:= |
| Out[20]= | 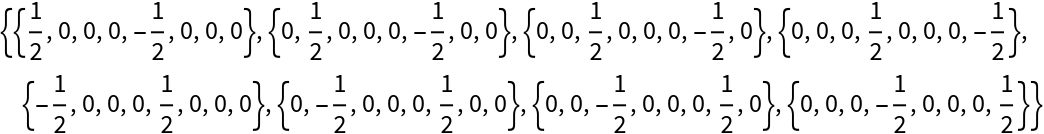 |
Return the ordered matrix representation (assuming a state of size 2) assuming that the measurement operator is applied instead to the second qubit of the state:
| In[21]:= | ![measurement2 = ResourceFunction[
"QuantumMeasurementOperator"][{{1/2, -1/2}, {-1/2, 1/2}}, {2}, ResourceFunction["QuantumBasis"]["PauliX"]];
measurement2[{"OrderedMatrixRepresentation", 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/b11/b11252e7-529e-4cc9-bbd6-fc2482e889d4/2359b6365d2c54d8.png) |
| Out[21]= |
Create a measurement operator based on the Pauli-X gate for qubits:
| In[22]:= |
| Out[22]= |
Create a measurement operator based on the Pauli-X gate for 3-dimensional qudits (non-Hermitian):
| In[23]:= |
| Out[23]= |
Create a measurement operator in the basis of the quantum Fourier transform on 1 qubit:
| In[24]:= |
| Out[24]= |
Create a measurement operator in the basis of the quantum Fourier transform on 2 qubits:
| In[25]:= |
| Out[25]= | 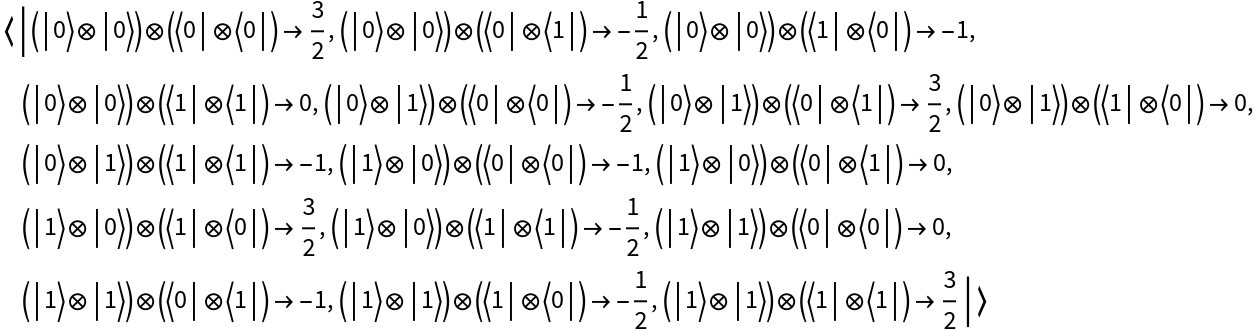 |
Create a measurement operator in the Bell basis, with eigenvalues (i.e. measurement outcomes) x, y, z and w:
| In[26]:= |
| Out[26]= | 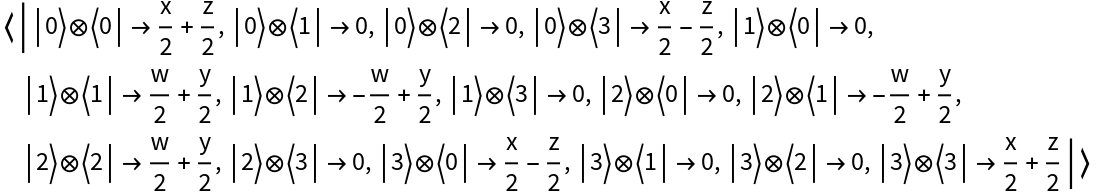 |
Return its list of eigenvalues:
| In[27]:= |
| Out[27]= |
Return its list of eigenvectors:
| In[28]:= |
| Out[28]= |
Create a measurement operator directly from a QuantumBasis object:
| In[29]:= | ![measurement = ResourceFunction["QuantumMeasurementOperator"][
ResourceFunction["QuantumBasis"]["Bell"], {1, 2}];
measurement["Operator"]](https://www.wolframcloud.com/obj/resourcesystem/images/b11/b11252e7-529e-4cc9-bbd6-fc2482e889d4/18469468a8467794.png) |
| Out[29]= |
Use eigenvalues (i.e. measurement outcomes) 1, -1, I, -I instead:
| In[30]:= | ![measurement2 = ResourceFunction[
"QuantumMeasurementOperator"][{ResourceFunction["QuantumBasis"][
"Bell"], {1, -1, I, -I}}, {1, 2}];
measurement2["Operator"]](https://www.wolframcloud.com/obj/resourcesystem/images/b11/b11252e7-529e-4cc9-bbd6-fc2482e889d4/17e0c98568db0ddf.png) |
| Out[30]= | 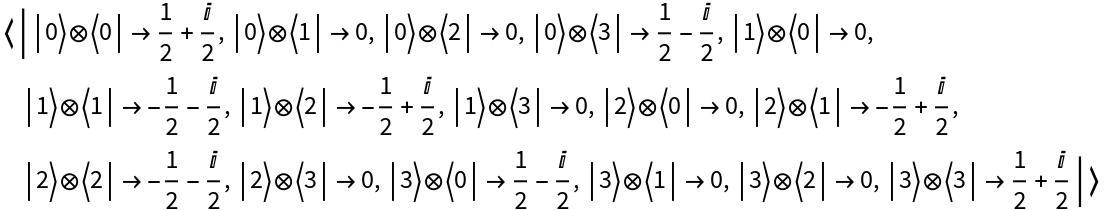 |
Return the lists of eigenvalues and eigenvectors:
| In[31]:= |
| Out[31]= |
| In[32]:= |
| Out[32]= |
Create a projection-valued discrete quantum measurement operator by explicitly specifying an association of matrix elements in a given (tensor product) basis and return its matrix representation:
| In[33]:= | ![measurement = ResourceFunction[
"QuantumMeasurementOperator"][<|TensorProduct[Ket[0], Ket[0]] -> 1,
TensorProduct[Ket[0], Ket[1]] -> -1, TensorProduct[Ket[1], Ket[0]] -> -1, TensorProduct[Ket[1], Ket[1]] -> 1|>];
measurement["MatrixRepresentation"]](https://www.wolframcloud.com/obj/resourcesystem/images/b11/b11252e7-529e-4cc9-bbd6-fc2482e889d4/30145a4e33ad5c7f.png) |
| Out[33]= |
Return its basis element association:
| In[34]:= |
| Out[34]= |
Return its operator association:
| In[35]:= |
| Out[35]= |
Create a positive operator-valued discrete quantum measurement operator by explicitly specifying an association of matrix operators in a given basis and return its list of elements:
| In[36]:= | ![measurement2 = ResourceFunction[
"QuantumMeasurementOperator"][<|
TensorProduct[Ket[0], Ket[0]] -> {{0, 0}, {0, 1}}, TensorProduct[Ket[0], Ket[1]] -> {{1, -1}, {-1, 1}}, TensorProduct[Ket[1], Ket[0]] -> {{0, 1}, {1, 0}}|>];
measurement2["POVMElements"]](https://www.wolframcloud.com/obj/resourcesystem/images/b11/b11252e7-529e-4cc9-bbd6-fc2482e889d4/0c833c421a6a45e1.png) |
| Out[36]= |
Return its basis element association:
| In[37]:= |
| Out[37]= |
Return its operator association:
| In[38]:= |
| Out[38]= |
Discrete quantum measurement operators can be applied to QuantumDiscreteState objects:
| In[39]:= | ![measurement = ResourceFunction["QuantumMeasurementOperator"][
"RandomHermitian", {1, 2}];
state = ResourceFunction["QuantumDiscreteState"][{"RandomPure", 2}];
measurementOutcome = measurement[state]](https://www.wolframcloud.com/obj/resourcesystem/images/b11/b11252e7-529e-4cc9-bbd6-fc2482e889d4/7b818c5a28d1c563.png) |
| Out[39]= |
However, measurement operators can also be applied directly to QuantumMeasurement objects to obtain a joint distribution:
| In[40]:= |
| Out[40]= |
By default, all discrete quantum measurement operators are assumed to apply to tensor products of 2-dimensional subsystems (i.e. qubits):
| In[41]:= |
| Out[41]= |
| In[42]:= |
| Out[42]= | 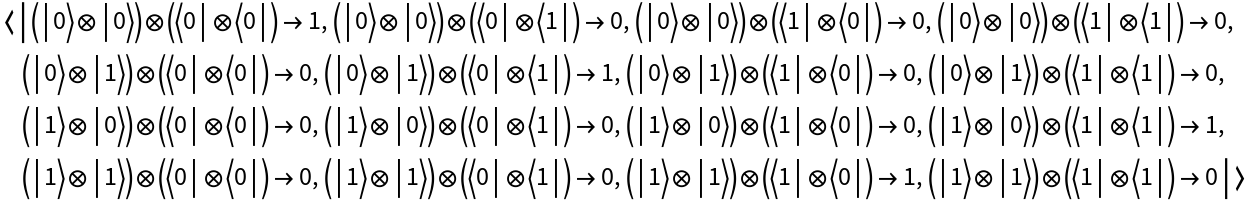 |
Create a discrete quantum measurement operator with the same matrix representation applying to a single 4-dimensional subsystem (i.e. qudit) instead:
| In[43]:= |
| Out[43]= |
| In[44]:= |
| Out[44]= |
Create a projection-valued discrete quantum measurement operator in the computational basis (default):
| In[45]:= |
| Out[45]= |
| In[46]:= |
| Out[46]= |
| In[47]:= |
| Out[47]= |
Transform the measurement operator to the Fourier basis:
| In[48]:= |
| Out[48]= |
| In[49]:= |
| Out[49]= |
| In[50]:= |
| Out[50]= |
Transform the measurement operator back to the computational basis:
| In[51]:= |
| Out[51]= |
| In[52]:= |
| Out[52]= |
| In[53]:= |
| Out[53]= |
The initial and final operators are the same:
| In[54]:= |
| Out[54]= |
Create a positive operator-valued discrete quantum measurement operator in the computational basis (default):
| In[55]:= |
| Out[55]= |
| In[56]:= |
| Out[56]= |
| In[57]:= |
| Out[57]= |
Transform the measurement operator to the Fourier basis:
| In[58]:= |
| Out[58]= |
| In[59]:= |
| Out[59]= |
| In[60]:= |
| Out[60]= |
Transform the measurement operator back to the computational basis:
| In[61]:= |
| Out[61]= |
| In[62]:= |
| Out[62]= |
| In[63]:= |
| Out[63]= |
The initial and final operators are the same:
| In[64]:= |
| Out[64]= |
Represent the Pauli-Z measurement gate in the Heisenberg picture:
| In[65]:= |
| Out[65]= |
| In[66]:= |
| Out[66]= |
Transform the measurement operator to the interaction picture:
| In[67]:= |
| Out[67]= |
| In[68]:= |
| Out[68]= |
Represent a 2-qubit random Hermitian operator in the computational basis:
| In[69]:= |
| Out[69]= |  |
| In[70]:= |
| Out[70]= |
Represent the same operator in the Pauli-X basis instead:
| In[71]:= | ![measurement2 = ResourceFunction["QuantumMeasurementOperator"][measurement, ResourceFunction["QuantumBasis"]["PauliX", 2]];
measurement2["Operator"]](https://www.wolframcloud.com/obj/resourcesystem/images/b11/b11252e7-529e-4cc9-bbd6-fc2482e889d4/09434f8b2865dc94.png) |
| Out[71]= |  |
| In[72]:= |
| Out[72]= |
Measurement operators in a given quantum-mechanical picture can be applied to QuantumDiscreteState objects that are also in the same picture:
| In[73]:= |
| Out[73]= |
| In[74]:= |
| Out[74]= |
| In[75]:= |
| Out[75]= |
However, they cannot be applied to QuantumDiscreteState objects if the pictures do not match (returns unevaluated):
| In[76]:= |
| Out[76]= |
| In[77]:= |
| Out[77]= | 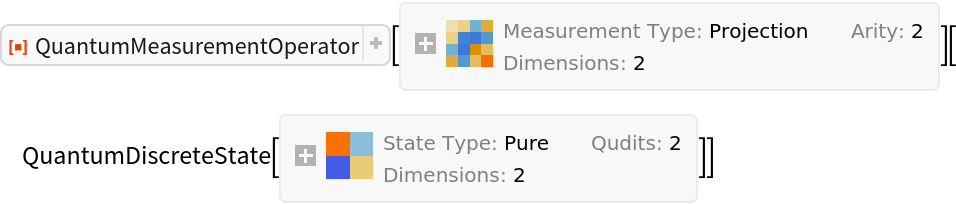 |
Represent a Pauli-X measurement gate (a π rotation around the x axis of the Bloch sphere) on qubits for qubit number 3:
| In[78]:= |
| Out[78]= |
Represent a Pauli-X measurement gate on 3-dimensional qudits for qudit number 3 (not Hermitian):
| In[79]:= |
| Out[79]= |
Represent a Pauli-Y measurement gate (a π rotation around the y axis of the Bloch sphere) on qubits for qubit number 3:
| In[80]:= |
| Out[80]= |
Represent a Pauli-Z measurement gate (a π rotation around the z-axis of the Bloch sphere) on qubits for qubit number 3:
| In[81]:= |
| Out[81]= |
Represent a Pauli-Z measurement gate on 3-dimensional qudits for qudit number 3 (not Hermitian):
| In[82]:= |
| Out[82]= | 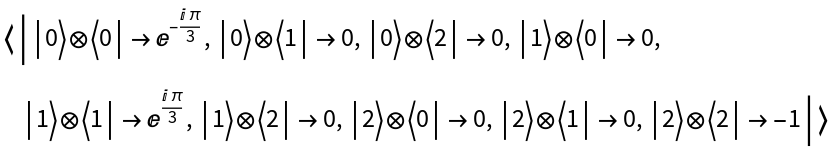 |
Represent a Hadamard measurement gate (a single-qubit quantum Fourier transform) for qubit number 1:
| In[83]:= |
| Out[83]= |
Represent a single-qubit random Hermitian operator (selected from a Gaussian Hermitian ensemble) for qubit 2:
| In[84]:= |
| Out[84]= |
Represent a two-qubit random Hermitian operator (selected from a Gaussian Hermitian ensemble) for qubits 2 and 3:
| In[85]:= |
| Out[85]= |  |
Represent a single-qudit random Hermitian operator (selected from a Gaussian Hermitian ensemble) on 3-dimensional qudits for qudit 2:
| In[86]:= |
| Out[86]= |  |
Represent a two-qudit random Hermitian operator (selected from a Gaussian Hermitian ensemble) on 3-dimensional qudits for qudits 2 and 3:
| In[87]:= |
| Out[87]= |  |
Represent a single-qubit computational basis measurement (with default eigenvalues) for qubit number 3:
| In[88]:= |
| Out[88]= |
Represent a two-qubit computational basis measurement (with default eigenvalues) for qubits 3 and 4:
| In[89]:= |
| Out[89]= | 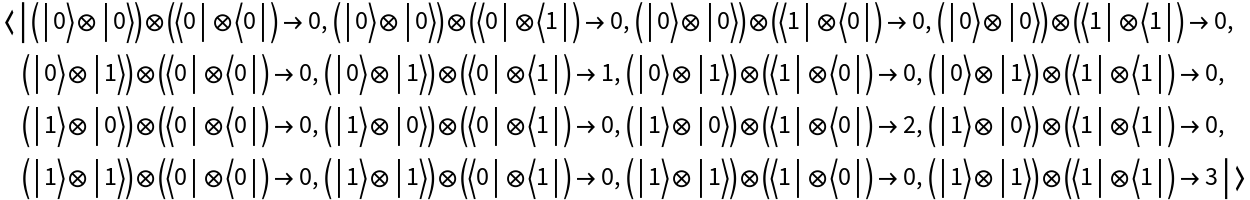 |
Represent a two-qubit computational basis measurement (with eigenvalues x, y, z, w) for qubits 3 and 4:
| In[90]:= |
| Out[90]= | 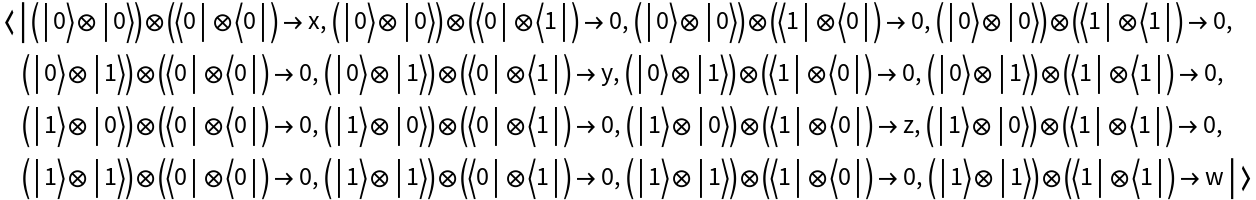 |
Represent a single-qudit computational basis measurement (with default eigenvalues) on 3-dimensional qudits for qudit number 3:
| In[91]:= |
| Out[91]= |
Represent a two-qudit computational basis measurement (with default eigenvalues) on 3-dimensional qudits for qudits 3 and 4:
| In[92]:= |
| Out[92]= |  |
Represent a single-qudit computational basis measurement (with eigenvalues x, y, z) on 3-dimensional qudits for qudit number 3:
| In[93]:= |
| Out[93]= |
Represent a single-qudit Bell basis measurement (with default eigenvalues) for qudit number 3:
| In[94]:= |
| Out[94]= |
Represent a single-qudit Bell basis measurement (with eigenvalues x, y, z, w) for qudit number 3:
| In[95]:= |
| Out[95]= | 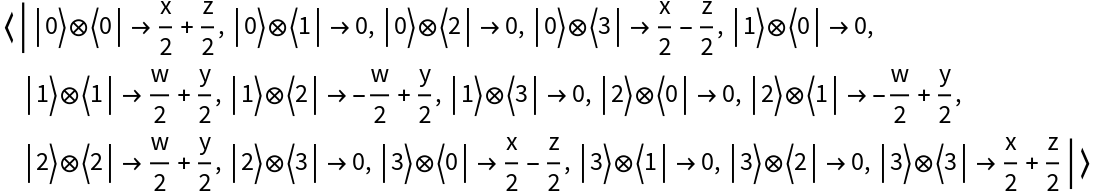 |
Represent a single-qubit Pauli basis measurement (with default eigenvalues) for qubit number 3:
| In[96]:= |
| Out[96]= |
Represent a two-qubit Pauli basis measurement (with default eigenvalues) for qubits 3 and 4:
| In[97]:= |
| Out[97]= | 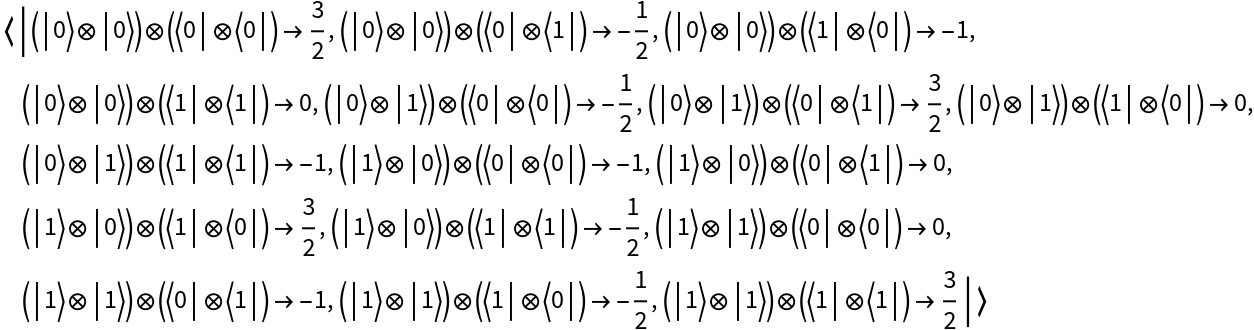 |
Represent a two-qubit Pauli basis measurement (with eigenvalues x, y, z, w) for qubits 3 and 4:
| In[98]:= |
| Out[98]= | 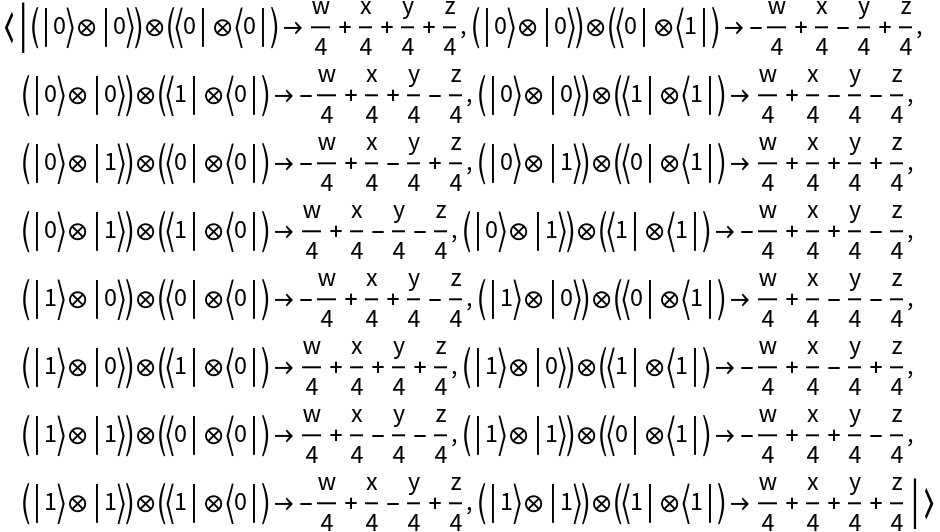 |
Represent a single-qubit Fourier basis measurement (with default eigenvalues) for qubit number 3:
| In[99]:= |
| Out[99]= |
Represent a two-qubit Fourier basis measurement (with default eigenvalues) for qubits 3 and 4:
| In[100]:= |
| Out[100]= |  |
Represent a two-qubit Fourier basis measurement (with eigenvalues x, y, z, w) for qubits 3 and 4:
| In[101]:= |
| Out[101]= | 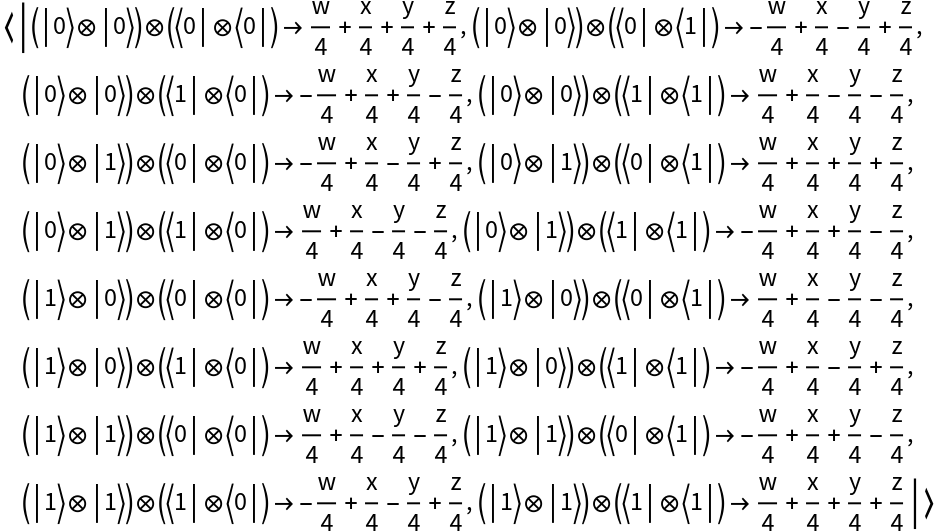 |
Represent a single-qudit Fourier basis measurement (with default eigenvalues) on 3-dimensional qudits for qudit number 3:
| In[102]:= |
| Out[102]= | 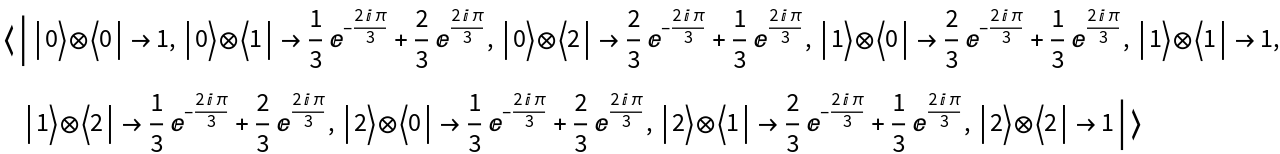 |
Represent a two-qudit Fourier basis measurement (with default eigenvalues) on 3-dimensional qudits for qudits 3 and 4:
| In[103]:= |
| Out[103]= |  |
Represent a single-qudit Fourier basis measurement (with eigenvalues x, y, z) on 3-dimensional qudits for qudit number 3:
| In[104]:= |
| Out[104]= | 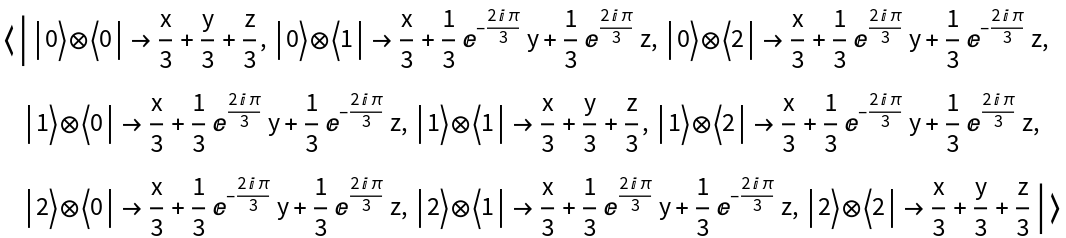 |
QuantumMeasurementOperator objects can be constructed purely symbolically (without explicit matrix elements):
| In[105]:= |
| Out[105]= |
View the measurement operator association:
| In[106]:= |
| Out[106]= |
Standard operations can still be performed on purely symbolic measurement operators:
| In[107]:= |
| Out[107]= |
| In[108]:= |
| Out[108]= | 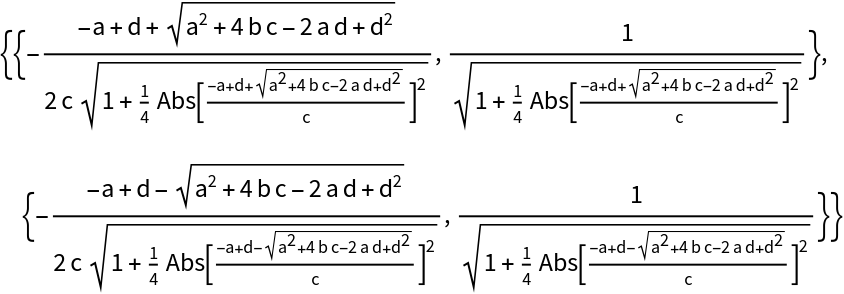 |
View a list of properties that can be extracted from a QuantumMeasurementOperator object:
| In[109]:= |
| Out[109]= |
| In[110]:= |
| Out[110]= |  |
Return the operator association:
| In[111]:= |
| Out[111]= |  |
Return which QuantumBasis the measurement operator is defined with respect to:
| In[112]:= |
| Out[112]= |
Return which quantum mechanical picture the measurement operator is defined with respect to:
| In[113]:= |
| Out[113]= |
Return the association of names and basis elements:
| In[114]:= |
| Out[114]= |
Return the matrix representation:
| In[115]:= |
| Out[115]= |  |
Return the ordered matrix representation (when applied to qubits 2 and 3) assuming a state consisting of 3 qubits:
| In[116]:= |
| Out[116]= |  |
Return the ordered matrix representation (when applied to qubits 2 and 3) assuming a state consisting of 4 qubits:
| In[117]:= |
| Out[117]= |  |
Return arity (number of input subsystems):
| In[118]:= |
| Out[118]= |
Return the number of dimensions:
| In[119]:= |
| Out[119]= |
Return the order in which the measurement operator is applied to subsystems:
| In[120]:= |
| Out[120]= |
Determine whether the measurement operator is Hermitian:
| In[121]:= |
| Out[121]= |
Determine whether the measurement operator is unitary:
| In[122]:= |
| Out[122]= |
Return the list of eigenvalues:
| In[123]:= |
| Out[123]= |
Return the list of eigenvectors:
| In[124]:= |
| Out[124]= |  |
Determine whether the measurement operator is projection-valued:
| In[125]:= |
| Out[125]= |
Determine whether the measurement operator is positive operator-valued:
| In[126]:= |
| Out[126]= |
Define a positive operator-valued measurement operator instead:
| In[127]:= |
| Out[127]= |
Return the list of operator matrices:
| In[128]:= |
| Out[128]= |
Return the ordered list of operator matrices (when applied to qubit 2) assuming a state consisting of 2 qubits:
| In[129]:= |
| Out[129]= |
Return the ordered list of operator matrices (when applied to qubit 2) assuming a state consisting of 3 qubits:
| In[130]:= |
| Out[130]= |  |
Return the list of eigenvalues for each operator:
| In[131]:= |
| Out[131]= |
Return the list of eigenvectors for each operator:
| In[132]:= |
| Out[132]= |
This work is licensed under a Creative Commons Attribution 4.0 International License