Wolfram Language Paclet Repository
Community-contributed installable additions to the Wolfram Language
Logical Rules for Solving a Sudoku
In[1]:=
Needs["FredSimons`SudokuHints`"]
Introduction
In the tech note , we have seen that a sudoku puzzle is actually nothing but a list of groups of nine cells. The goal of the puzzle is to place in each cell one of the numbers 1, …,9 such that at the end each group will contain all numbers 1,…,9, or equivalent, that all numbers in a group will be different.
Normally, for some of the cells the value is given already. These are called the clues of the sudoku. The set of clues should restrict the number of solutions of the sudoku such that there is only one solution left.
For each empty cell we will call the set of numbers that can be placed in that cell the candidates of that cell. We will frequently use the terminology that two cells see each other. That simply means that the two cells are in one group. It follows that when the number n is placed in a cell, that number n can not be placed in all cells that see that cell; we can skip that candidate from those cells. This is a typical example of a logical argument. Solving a sudoku amounts to using logical arguments for skipping candidates in a cell until only one candidate is left for that cell. That candidate has to be placed in that cell.
The above observation can be generalized a little bit to what I like to refer to as the sees all argument:
When we are sure that a number n has to be placed in at least one cell of a list of cells, then the number n cannot be a candidate in all cells that see all cells of the list.
Quite a lot, and at least all of the most frequently used logical rules , are based on this argument. Solving a sudoku by hand frequently requires looking for sets of cells of which we are sure that a candidate has to be placed somewhere in that set.
Single and HiddenSingle
The simplest application of sees all is if we have one cell of which we are sure that a candidate has to be placed there. In that case, we can not only remove that candidate for all cells that see this cell, but we can also place that number in that cell. This may happen in two situations.
- We have a cell in which we have only one candidate. Then we have a so called single . We can place that number in that cell and remove the candidate from all other cells that see this cell. It is implemented in the function :
In[1]:=
 | Single |
Out[1]=
 |
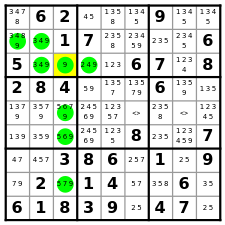Single-9: R2C1(3,4,8), R2C2(3,4), R3C2(3,4), R3C3(9), R3C4(2,4), R5C3(5,6,7), R6C3(5,6), R8C3(5,7) |
In cell R3C3 the only candidate is 9, so 9 can be removed as a candidate from all cells that see R3C3.
- There is only one cell in a group where the candidate turns up. That is called a hiddden single, hidden because of the cell may have other candidates as well. It implies that that candidate has to be placed in that cell, and can be removed from all cells that see this cell. It is implemented in the function .
In[2]:=
| HiddenSingle |
Out[2]=
 |
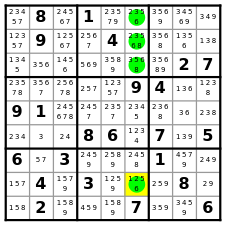HiddenSingle-6: R1C6(2,3,5), R2C6(2,3,5,8), R3C6(3,5,8), R8C6(6) |
In row 8, we have a candidate 6 only in cell R8C6. Therefore, the number 6 has to be placed in that cell and can be removed as a candidate from all cells that see R8C6.
CandidateSets (generalizes locked candidates)
For a given group and candidate, we will call the set of cells of the group that contain the candidate a candidate set. Obviously, the candidate has to be placed in one of the cells of the set and therefore can be removed from all cells that see the complete candidate set.
In[1]:=
| CandidateSet |
Out[1]=
 |
CandidateSet-3: R1C7(1,5,8,9), R1C8(1,8,9), R1C9(1,5,7,9) |
The two yellow cells form the candidate set for the candidate 3 in the second block, and therefore the number 3 can be removed as a candidate from the three green cells, that see all cells of the candidate set.
In this example the candidate set for the candidate 3 in block 2 is completely contained in the first row. That is often formulated in a complicated way: the candidate 3 of block 2 is locked in row 1 and therefore can be removed from all other cells of row 1. In this form, the reduction rule is called locked candidates.
For a standard sudoku, candidate sets only give reductions when they are contained in another group. For standard sudoku's, the rule CandidatesSet is the same as the rule locked candidates.
For non-standard sudoku's, CandidatesSet is more general than locked candidates.
In[2]:=
| CandidateSet |
Out[2]=
For this jigsaw-sudoku, the for yellow cells form the candidate set for candidate 4 in the thirs region. Cell R2C4 sees all four yellow cells, and therefore the candidate 4 can be removed from this cell. The four yellow cells are not contained in any other group, so this result cannot be obtained with locked candidates.
In[3]:=
| CandidateSet |
Out[3]=
 |
CandidateSet-3: R8C1(4,6,8) |
In this diagonal sudoku, the two yellow cells are the candidate set for the candidate 3 of the main diagonal. This set is seen from the cell R8C1, so the candidate 3 can be removed from this cell. Since the candidate set is not contained in any other group, this result is not found with locked candidates.
Finally an implementation remark: the rule is not implemented as a separate rule, but as a particular case of CandidateSet with only one cell.
Tuples
A tuple consists of n cells in a group in which all together we have n candidates. Then necessarily these candidates have to be placed in these cells, for if one candidate would be placed outside these cells, we arrive at a situation that we have n-1 candidates for filling n cells, which is clearly impossible. Therefore each of the candidates can be removed from all cells that see the tuple cells.
In[1]:=
| Pair |
Out[1]=
 |
Pair-46: R4C4(2,5,7), R4C5(2,5,9), R4C6(5,9), R5C2(7,8), R5C3(7,8), R5C7(3,7,8) |
In row 5 or block 5 we have two candidates 4 and 6 for the two yellow cells. Therefore, these candidates have to be placed in these cells and can be removed from all cells that see the yellow cells, marked with green disks.
In[2]:=
| Triple |
Out[2]=
 |
Triple-458: R4C7(1,6), R7C7(1,2,6), R9C7(1,2,6) |
In column 7, the candidates 4, 5 and 8 are the only candidates in the three yellows cells, and therefore have to be placed in these cells. So these candidates can be removed from all cells that see all yellow cells, i.e. from the green cells.
Hidden Tuples
A hidden tuple is just a tuple, but hidden because some of the cells of the tuple contain other candidates. More precisely:
A hidden tuple consists of n candidates that turn up in exactly n cells of a group. Therefore, these candidates have to be placed in these cells and all other candidates can be removed from the hidden tuple cells.
That means that a hidden tuple reduces to a tuple.
In block 9, the candidates 2, 3 and 4 appear only in the three yellow cells and therefore have to be placed there. All other candidates can be removed from the yellow cells.
Strictly speaking, hidden tuples are not based on sees all. But when in a group we have a hidden tuple, the other cells in the group form a tuple, that by means of sees all leads to the same reductions as the hidden tuple. Verify this in the examples.
Other Rules
With the rules so far, we can already solve the majority of regularly published sudoku puzzles. For solving the majority of the rest, in this section we discuss some more advanced rules.
ThreeGroups
ThreeGroups
This is a one candidate rule requiring three groups. Consider a candidate k and look for two groups in which the candidate k turns up twice, in the cells a and b in the first group and c and d in the second group. When b and c are in a third group, then the candidate k has to be placed in at least one of the cells a and d. For if k is not in a, it must be in b, so it cannot be in c, so it must be in d. Therefore, the candidate k can be removed from all cells that see both a and d.
In the output, the cells a and d will be in yellow and the cells b and c in light yellow.
When the candidate 8 is not placed in R4C1, it has to be placed in R4C6, so it cannot be in R9C6, so it must be in R9C2. So we are sure that the candidate 8 has to be placed in at leat one of the yellow cells, so it can be removed from all cells that see the yellow cells, in particular R6C2 and R7C1, the green cells.
XRule and SwordFish
XRule and SwordFish
Recall that a sudoku is just a list of groups of nine cells and that we want to assign to each cell one of the numbers 1, …, 9 such that all assigned number in each group will be different. All rules discussed so far were formulated in terms of groups only, and therefore can be used for any sudoku, no use was made of special structures in the groups. The rules XRule and SwordFish are different. They will be formulated in terms of rows and columns and can be used only for 9x9 sudoku's with 9 rows and 9 columns.
Let us start with XRule. That is a one candidate rule and has to do with the presence of a structure often refered to as an X. An X for a candidate k consists of four cells with candidate k, arranged in two rows and two columns, such that the two rows (or columns) do not have other cells with the candidate k. Then the candidate k can be removed form all other cells in the columns (or rows).
In this example, the four yellow cells form an X for the candidate 9: they are the only cells on row 3 and row 8 with this candidate and they are in only two columns: column 5 and column 6. These four cells can be seen as the vertices of a rectangle. We easily verify that when the candidate 9 is placed in the upper left cell of the rectangle, we also have a 9 in the lower right cell of the rectangle, and when it is in upper right cell of the rectangle, we also have a 9 at the lower left point of the rectangle. Therefore, the candidate 9 has to be placed on one of the diagonals of the rectangle, which explains the name X.
It follows that in both columns the candidate 9 must be placed on one of the yellow cells, which implies that the candidate 9 can be removed from all other cells in the columns.
In this paclet, the rule XRule is superfluous. Observe that the upper, left and lower side of the rectangle give a ThreeGroups configuaration, as do the upper, right and lower side of the rectangle. The XRule is a combination of two Threegroups:
The rule that is usually refered to as a SwordFish is a generalization of the XRule. Instead of two rows and two columns it has three rows and three columns. More precisely: a swordfish for the candidate k consists of at most 9 cells with candidate k, arranged in three rows and three columns. When the three rows (or columns) do not have other cells with candidate k, the candidate k can be eliminated from all other cells in the three columns (or rows).
The yellow cells form a swordfish with 9 cells for the candidate 6. The candidate 6 does not appear in other cells of the three rows. Therefore, for each of the three columns the candidate has to be placed in one of the yellow cells. For if a column would exist in which the candidate is not placed in a yellow cell, on three rows the candidate has to be placed in one of two columns, which is clearly impossible.
Therefore, the candidate can be removed from all other cells in the three columns.
A swordfish must have at least three cells in three rows and three columns. In all cases, the argumentation remains the same. This is an example with six cells:
XYChains
XYChains
This rule is based on sequences of cells, called XYchains, that have two candidates and such that any two succesive cells see each other. When the first and the last cell of an XYchain both contain the candidate k, it follows that k must be placed in one of the endpoints of the chain, so that the candidate k can be removed from all cells that see the endpoints.
The three yellow cells R3C2, R1C3 and R1C7 each have two candidates and see each other in turn. In both endpoints we have a candidate 4. When 4 is not placed in cell R3C2, the number 6 has to placed in that cell, which implies that in R1C3 we will have a 1 and in R1C4 we wil have a 4. So we are sure that in at least one of the endpoints the number 4 has to be placed, so 4 can be removed as a candidate from the two cells R1C2 and R3C7, that see both endpoints of the chain.
An XYchain can be quite long:
The nine yellow cells, with the dark yellow cells as endpoints, form an XYchain of length 11 for the candidate 7. When cell R2C4 does not have a 7, it has a 2. Running over all light yellow cells, this implies that R9C8 has a 7, which gives the reduction n cell R9C4.
XYZWings
XYZWings
The three yellow cells with the candidates 2, 4 and 6 form an XYZwing. The common candidates is 6. When R2C9 is not 6, it becomes 2, which results in the two other yellow cells being a pair with candidates 4 and 6, so in that case the candidate 6 has to be placed in one of these cells. So we are sure that the candidate 6 has to be places in one of the yellow cells, and there can be renoved from all cells that see the three yellow cells, in particular from R1C8.
ConjugateLists
ConjugateLists
Two lists of cells are said to be conjugate with respect to a candidate if the candidate has to be placed in all cells of the first list and cannot be placed in the cells of the second list, or conversely. The simplest example of conjugate lists is seen in the rule DoubleCandidate: the candidate has to be placed in one of the two cells.
The example shows two conjugate lists for the candidate 5. Both are in orange; the cells of the first list are orange in the lower left vertex and the cells of the other list are orange in the lower right vertex.
The construction of conjugate lists is pretty straightforward. In this example, in block 2 the candidate 5 is only in the cells R2C4 and R3C5. We color the first cell orange lower right and the second cell orange lower left. Since 5 is a double candidate in row 2, we color R2C2 orange lower left. Since 5 is a double candidate in row 3, we color the cell R3C9 orange lower right, and so on, running over all groups in which 5 is a double candidate. Due to this construction, we are sure that the candidate 5 has to be placed in all cells with orange lower left vertex and cannot be placed in the cells with orange lower right vertex, or conversely.
Conjugate lists may give reductions in two different situations.
- When a cell sees a cell of both lists, the candidate cannot be placed in that cell. In the example this situation turns up in row 7: the cell R8C4 sees both the orange lower left cell R8C2 and the orange lowe right cell R8C5. Since the candidate 5 has to be places in one of these cells, the candidate 5 can be eliminated:
- When two cells of of one of the conjugate lists turn up in a group, then the candidate cannot be placed in the cells of that group. In the example, we have this situation e.g. in block 1 and in row 1. It implies that the candidate 5 cannot be placed in the cells with orange lower left vertices.
In this example, it follows that the candidate 5 has to be placed in the cells with orange right cells. That is not implemented in this rule. When we eliminate a candidate from one of the conjugate lists, the cells of the other list automically become (hidden) singles.