Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Partially trace out specified subsystems of a quantum basis, state or operator
ResourceFunction["QuantumPartialTrace"][QuantumBasis[…],order] returns the specified QuantumBasis object with the subsystems indexed by order traced out. | |
ResourceFunction["QuantumPartialTrace"][QuantumDiscreteState[…],order] returns the specified QuantumDiscreteState object with the subsystems indexed by order traced out. | |
ResourceFunction["QuantumPartialTrace"][QuantumDiscreteOperator[…],order] returns the specified QuantumDiscreteOperator object with the subsystems indexed by order traced out. | |
ResourceFunction["QuantumPartialTrace"][QuantumMeasurementOperator[…],order] returns the specified QuantumMeasurementOperator object with the subsystems indexed by order traced out. | |
ResourceFunction["QuantumPartialTrace"][QuantumHamiltonianOperator[…],order] returns the specified QuantumHamiltonianOperator object with the subsystems indexed by order traced out. | |
ResourceFunction["QuantumPartialTrace"][QuantumCircuitOperator[…],order] returns the (operator representation of the) specified QuantumCircuitOperator object with the subsystems indexed by order traced out. |
Partially trace out qubits 5, 3 and 1 from a five-qubit Pauli-X QuantumBasis object to obtain a two-qubit QuantumBasis object:
| In[1]:= |
| Out[1]= | 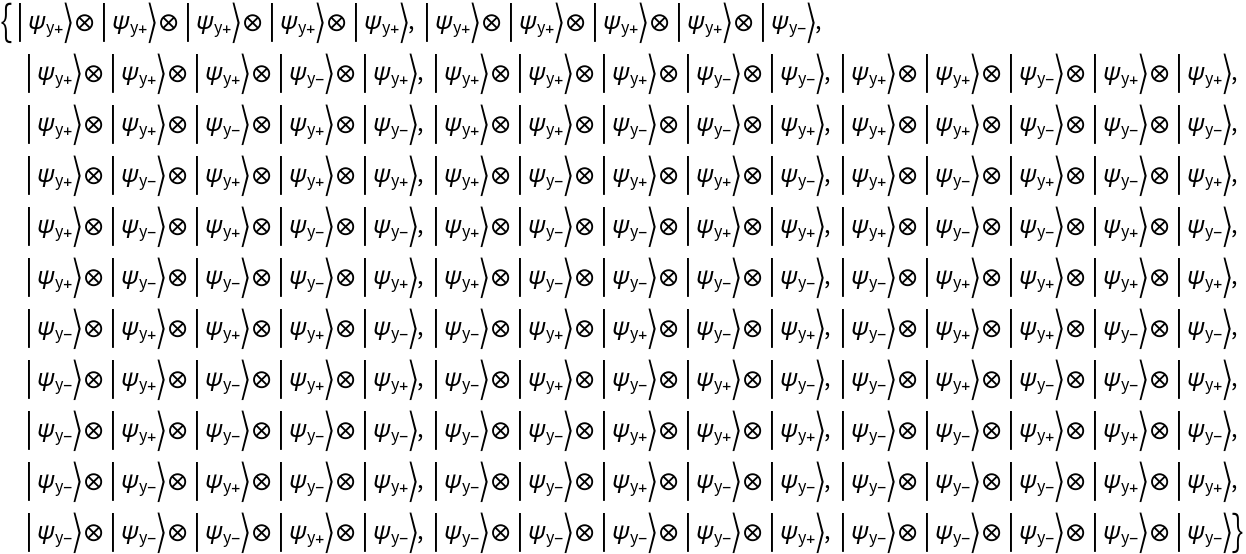 |
| In[2]:= |
| Out[2]= |
| In[3]:= |
| Out[3]= | 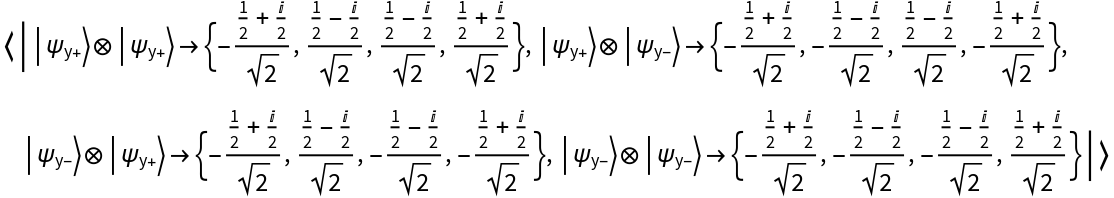 |
Partially trace out qubits 3 and 2 from a three-qubit pure QuantumDiscreteState object to obtain a single-qubit pure QuantumDiscreteState object:
| In[4]:= | ![state = ResourceFunction["QuantumDiscreteState"][{1/2 + I/2, 0, 0, 1/2 + I/2, 1/2 - I/2, 0, 0, 1/2 - I/2}];
state["Amplitudes"]](https://www.wolframcloud.com/obj/resourcesystem/images/b64/b642c281-8912-476e-875b-30b89d137e2c/243c7f44de5e7e1e.png) |
| Out[4]= | 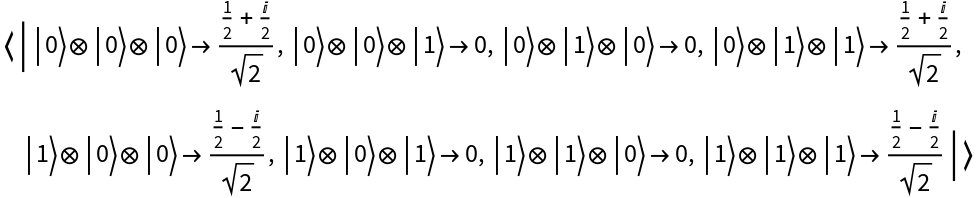 |
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |
On the other hand, if we partially trace out qubits 3 and 1 instead, then we obtain a single-qubit mixed QuantumDiscreteState object:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |
Partially trace out qubit 2 from a two-qubit mixed QuantumDiscreteState object to obtain a single-qubit mixed QuantumDiscreteState object:
| In[10]:= | ![state2 = ResourceFunction[
"QuantumDiscreteState"][{{1/8 + I/2, 1/2 - I/8, 1/4, -I/4}, {-1/2 + I/8, 1/8 + I/2, I/4, 1/4}, {1/4, -I/4, 3/8 - I/2, -1/2 - 3 I/8}, {I/4, 1/4, 1/2 + 3 I/8, 3/8 - I/2}}];
state2["Amplitudes"]](https://www.wolframcloud.com/obj/resourcesystem/images/b64/b642c281-8912-476e-875b-30b89d137e2c/6f66d89d0459d762.png) |
| Out[10]= | 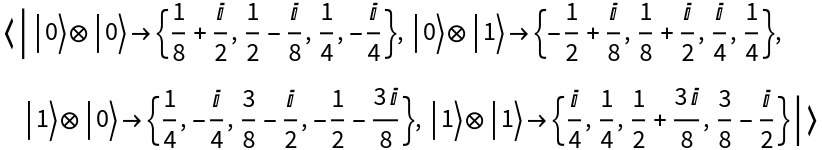 |
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= |
On the other hand, if we partially trace out qubit 1 instead, then we obtain a single-qubit pure QuantumDiscreteState object:
| In[13]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= |
Partially trace out qubit 1 from an arity-3 QuantumDiscreteOperator object to obtain an arity-2 QuantumDiscreteOperator object:
| In[15]:= | ![operator = ResourceFunction[
"QuantumDiscreteOperator"][{{1/Sqrt[2], 1/Sqrt[2], 0, 0, 0, 0, 0, 0}, {1/Sqrt[2], -1/Sqrt[2], 0, 0, 0, 0, 0, 0}, {0, 0, 1/Sqrt[2], 1/Sqrt[2], 0, 0, 0, 0}, {0, 0, 1/Sqrt[2], -1/Sqrt[2], 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 1/Sqrt[2], 1/Sqrt[2]}, {0, 0, 0, 0, 0, 0, 1/Sqrt[2], -1/Sqrt[2]}, {0, 0, 0, 0, 1/Sqrt[2], 1/Sqrt[2], 0, 0}, {0, 0, 0, 0, 1/Sqrt[2], -1/Sqrt[2], 0, 0}}];
operator["MatrixRepresentation"]](https://www.wolframcloud.com/obj/resourcesystem/images/b64/b642c281-8912-476e-875b-30b89d137e2c/3af2b3238b8cad5d.png) |
| Out[15]= | 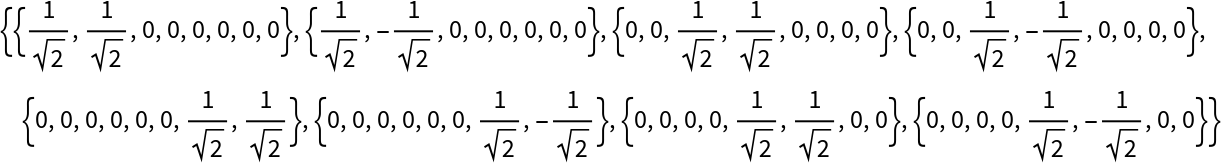 |
| In[16]:= |
| Out[16]= | 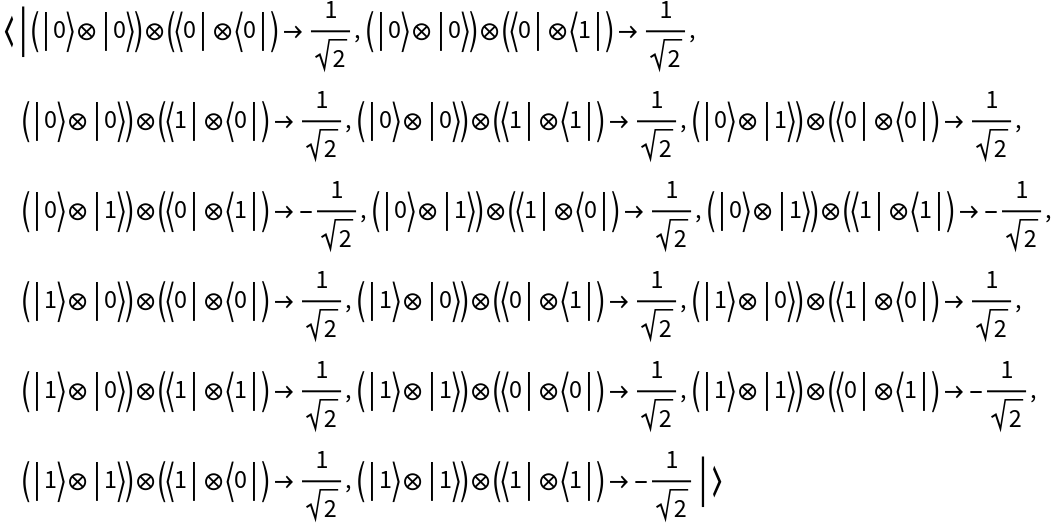 |
| In[17]:= |
| Out[17]= |
Partially trace out qubits 2 and 1 instead, to obtain an arity-1 QuantumDiscreteOperator object:
| In[18]:= |
| Out[18]= |
| In[19]:= |
| Out[19]= |
Partially trace out qubit 4 from an arity-4 projection-valued QuantumMeasurementOperator object to obtain an arity-3 QuantumMeasurementOperator object:
| In[20]:= | ![measurement = ResourceFunction[
"QuantumMeasurementOperator"][{{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 3/2, -1/2, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, -1/2, 3/2, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, -1, 0, 3/2, -1/2, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, -1, -1/2, 3/2, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 3, -1, -2,
0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, -1, 3, 0, -2, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, -2, 0, 3, -1, 0, 0, 0, 0}, {0, 0, 0,
0, 0, 0, 0, 0, 0, -2, -1, 3, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 9/2, -3/2, -3, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -3/2, 9/2, 0, -3}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -3,
0, 9/2, -3/2}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -3, -3/2,
9/2}}];
measurement["MatrixRepresentation"]](https://www.wolframcloud.com/obj/resourcesystem/images/b64/b642c281-8912-476e-875b-30b89d137e2c/4566bc1231793869.png) |
| Out[20]= | 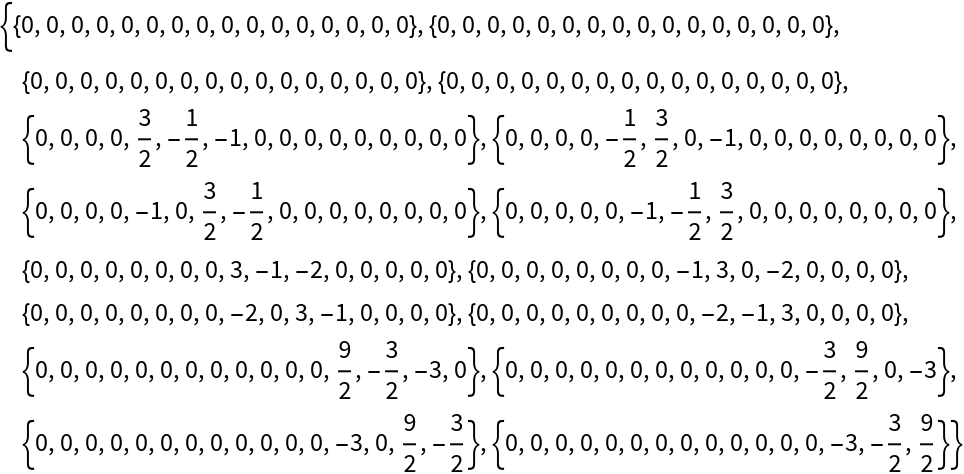 |
| In[21]:= |
| Out[21]= |
| In[22]:= |
| Out[22]= |
Partially trace out qubits 3 and 2 instead, to obtain an arity-2 QuantumMeasurementOperator object:
| In[23]:= |
| Out[23]= | 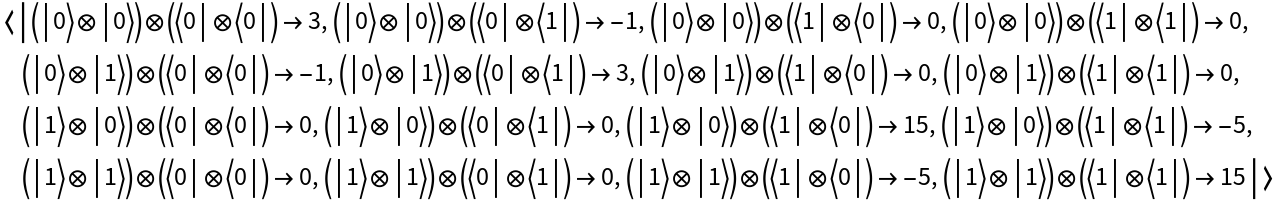 |
| In[24]:= |
| Out[24]= |
Partially trace out qubit 2 from an arity-2 positive operator-valued QuantumMeasurementOperator object to obtain an arity-1 positive operator-valued QuantumMeasurementOperator object:
| In[25]:= | ![measurement2 = ResourceFunction[
"QuantumMeasurementOperator"][{{{0, 0, 0, 0}, {0, 0, 0, 0}, {0, 0,
1, -1}, {0, 0, -1, 1}}, {{0, 1, 0, -1}, {1, 0, -1, 0}, {0, -1, 0, 1}, {-1, 0, 1, 0}}, {{0, 0, -1, 1}, {0, 0, 1, -1}, {0, 0, 0, 0}, {0, 0, 0, 0}}, {{-1, 0, 1, 0}, {0, -1, 0, 1}, {1, 0, -1, 0}, {0, 1, 0, -1}}}, 2];
measurement2["Operator"]](https://www.wolframcloud.com/obj/resourcesystem/images/b64/b642c281-8912-476e-875b-30b89d137e2c/202d00aee65ab887.png) |
| Out[25]= |  |
| In[26]:= |
| Out[26]= |
Partially trace out qubit 1 instead:
| In[27]:= |
| Out[27]= |
Partially trace out qubit 1 from an arity-2 QuantumHamiltonianOperator object to obtain an arity-1 QuantumHamiltonianOperator object:
| In[28]:= | ![hamiltonian = ResourceFunction[
"QuantumHamiltonianOperator"][{{1 + \[FormalT]^2, 0, 1 - \[FormalT]^2, 0}, {0, -1 - \[FormalT]^2, 0, -1 - \[FormalT]^2}, {1 - \[FormalT]^2, 0, 1 + \[FormalT]^2, 0}, {0, -1 - \[FormalT]^2, 0, -1 - \[FormalT]^2}}];
hamiltonian["Operator"]](https://www.wolframcloud.com/obj/resourcesystem/images/b64/b642c281-8912-476e-875b-30b89d137e2c/3a8454ec1c1c9fb6.png) |
| Out[28]= | 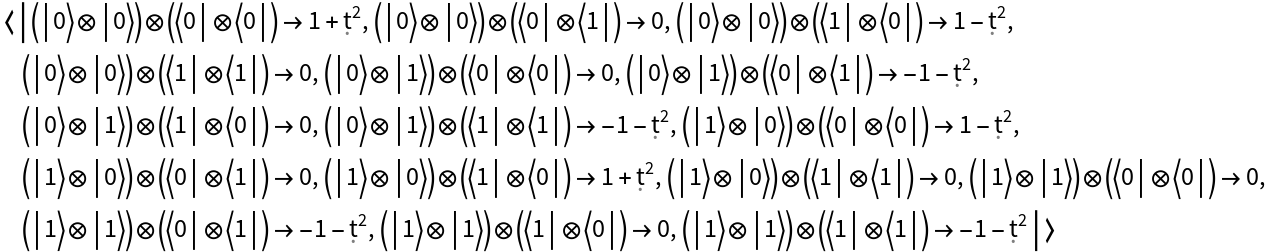 |
| In[29]:= |
| Out[29]= |
Partially trace out qubit 2 instead:
| In[30]:= |
| Out[30]= |
Partially trace out qubit 3 from an arity-3 QuantumCircuitOperator object to obtain an arity-2 QuantumDiscreteOperator object:
| In[31]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["CNOT", {2, 3}], ResourceFunction["QuantumDiscreteOperator"]["SWAP", {1, 3}], ResourceFunction["QuantumDiscreteOperator"][
"Fourier", {1, 2, 3}]}];
circuit["MatrixRepresentation"] // MatrixForm](https://www.wolframcloud.com/obj/resourcesystem/images/b64/b642c281-8912-476e-875b-30b89d137e2c/4aea328d5c2ad582.png) |
| Out[31]= |  |
| In[32]:= |
| Out[32]= |
| In[33]:= |
| Out[33]= | 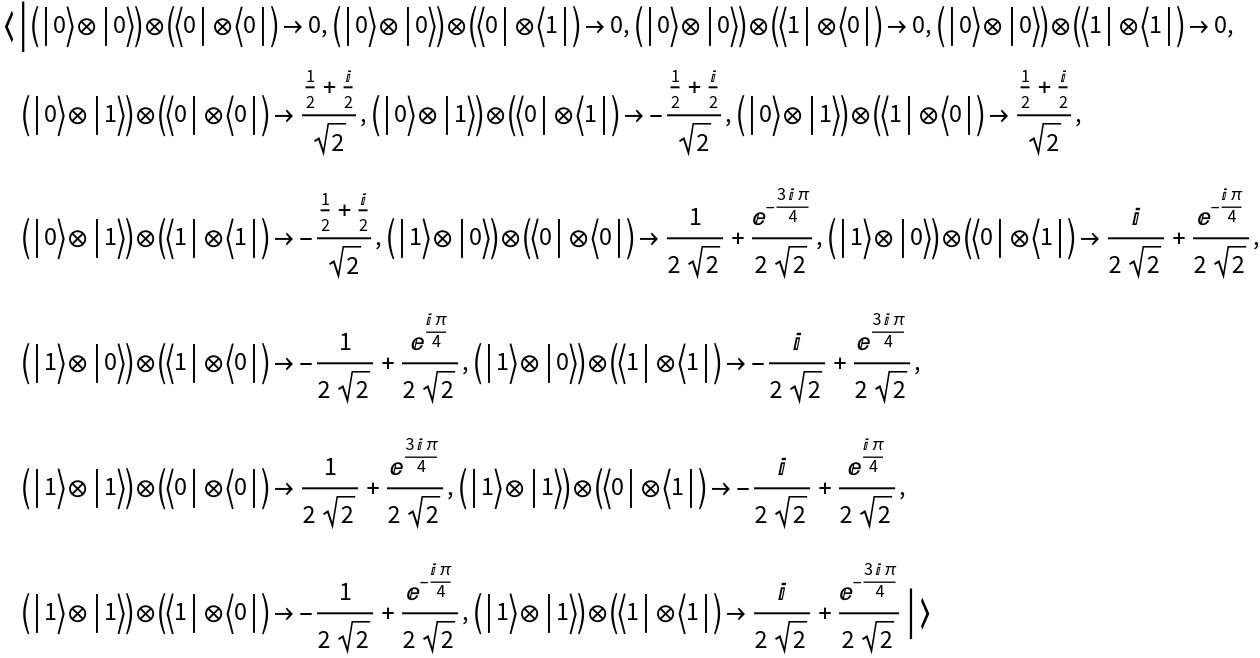 |
Partially trace out qubits 3 and 1 instead, to obtain an arity-1 QuantumDiscreteOperator object:
| In[34]:= |
| Out[34]= |
| In[35]:= |
| Out[35]= | 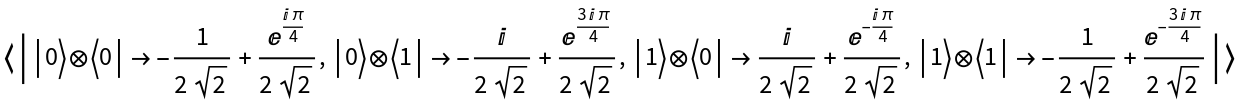 |
Partially trace over higher-dimensional quantum objects:
| In[36]:= | ![state = ResourceFunction["QuantumDiscreteState"][{1/3 Sqrt[5], I/Sqrt[15], (-I + Sqrt[2/3])/Sqrt[15], (1/3 + I/3)/
Sqrt[5], -(1 - I)/
Sqrt[15], (1 + I) (-I + Sqrt[2/3])/Sqrt[15], (1/3 - I/3)/
Sqrt[5], (1 + I)/Sqrt[15], (1 - I) (-I + Sqrt[2/3])/Sqrt[15]}, 3];
state["Amplitudes"]](https://www.wolframcloud.com/obj/resourcesystem/images/b64/b642c281-8912-476e-875b-30b89d137e2c/279a758f866f62cf.png) |
| Out[36]= | 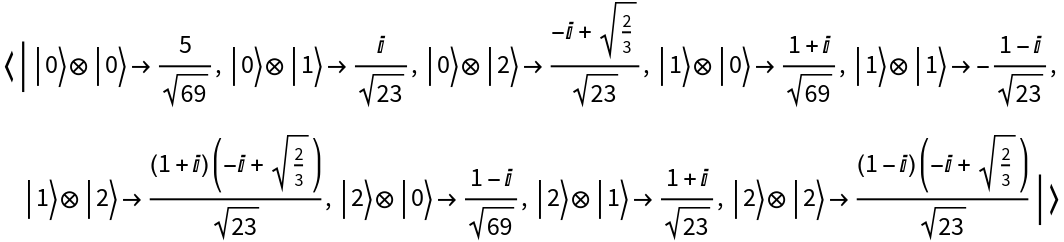 |
| In[37]:= |
| Out[37]= | 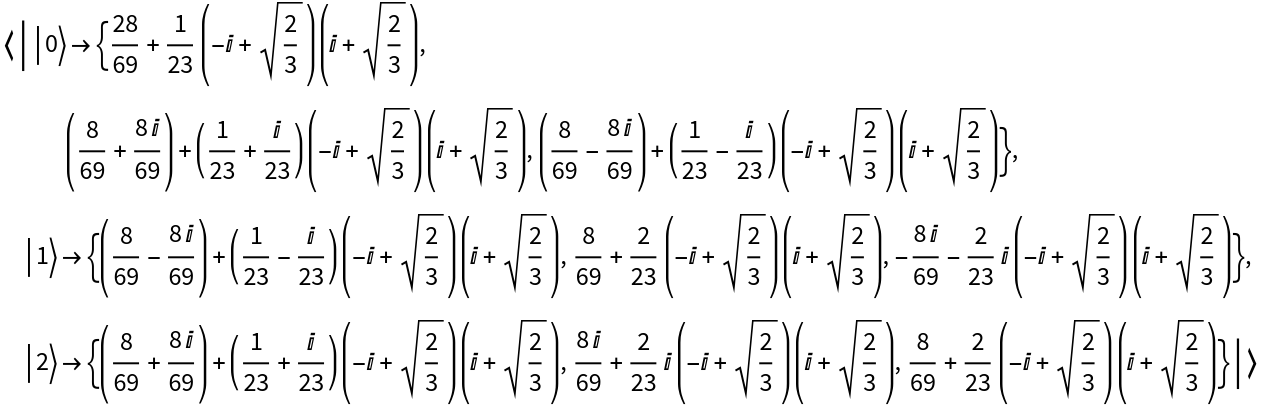 |
| In[38]:= |
| Out[38]= |
When taking the partial trace of a QuantumDiscreteState, QuantumDiscreteOperator, QuantumMeasurementOperator, QuantumHamiltonianOperator or QuantumCircuitOperator object, QuantumPartialTrace will also compute the partial trace of the associated QuantumBasis objects implicitly:
| In[39]:= | ![state = ResourceFunction["QuantumDiscreteState"][{1/2 + I/2, 1/2 + I/2, 1/2 - I/2, 1/2 - I/2}, ResourceFunction["QuantumBasis"]["PauliY", 2]];
state["Amplitudes"]](https://www.wolframcloud.com/obj/resourcesystem/images/b64/b642c281-8912-476e-875b-30b89d137e2c/7cf4eb5a81c91a6a.png) |
| Out[39]= |
| In[40]:= |
| Out[40]= |
| In[41]:= |
| Out[41]= |
The resulting basis is equivalent to partially tracing over the original basis:
| In[42]:= |
| Out[42]= |
This work is licensed under a Creative Commons Attribution 4.0 International License