Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Represent a discrete quantum circuit operator
ResourceFunction["QuantumCircuitOperator"][{gate1,gate2,…},order,qb] represents a discrete quantum circuit operator with gates (i.e. QuantumDiscreteOperator or QuantumMeasurementOperator objects) gatei, applied to the qudits indexed by order, defined with respect to a specified QuantumBasis qb. | |
ResourceFunction["QuantumCircuitOperator"][qco,qb] transforms a specified ResourceFunction["QuantumCircuitOperator"] qco into a new QuantumBasis qb. | |
ResourceFunction["QuantumCircuitOperator"][qco,pic] transforms qco into the new quantum mechanical picture pic. |
| "Operator" | association <|b11→e11,b12→e12,…|> of tensor products of basis names and matrix elements |
| "Basis" | which QuantumBasis the circuit operator is defined with respect to |
| "Picture" | which quantum mechanical picture the circuit operator is defined with respect to |
| "BasisElements" | list of basis elements bi |
| "MatrixRepresentation" | matrix representation mat of the circuit operator |
| "OrderedMatrixRepresentation" | matrix representation adjusted according to the order of the circuit operator, assuming an input state containing Max[order] qudits (subsystems) |
| {"OrderedMatrixRepresentation",n} | matrix representation adjusted according to the order of the circuit operator, assuming an input state containing n qudits (subsystems) |
| "OperatorRepresentation" | representation of the circuit operator as a QuantumDiscreteOperator |
| "Arity" | arity of the circuit operator |
| "Dimensions" | dimensionality of each qudit (subsystem) in the input state for the circuit operator |
| "Order" | order in which the circuit operator should be applied to qudits (subsystems) in the input state |
| "HermitianQ" | whether the circuit operator is Hermitian (self-adjoint) |
| "UnitaryQ" | whether the circuit operator is unitary (an automorphism of Hilbert space) |
| "Eigenvalues" | eigenvalues of the matrix representation of the circuit operator |
| "Eigenvectors" | eigenvectors of the matrix representation of the circuit operator |
| "Gates" | list of gates (QuantumDiscreteOperator and QuantumMeasurementOperator objects) contained within the circuit operator |
| "GateOperators" | list of associations <|b11→e11,b12→e12,…|> of tensor products of basis names and matrix elements for each QuantumDiscreteOperator or QuantumMeasurementOperator in the circuit |
| "GateBases" | list of QuantumBasis objects for each QuantumDiscreteOperator or QuantumMeasurementOperator in the circuit |
| "GatePictures" | list of quantum mechanical pictures for each QuantumDiscreteOperator or QuantumMeasurementOperator in the circuit |
| "GateBasisElements" | list of lists of basis elements bi for each QuantumDiscreteOperator or QuantumMeasurementOperator in the circuit |
| "GateMatrixRepresentations" | list of matrix representations mat for each QuantumDiscreteOperator or QuantumMeasurementOperator in the circuit |
| "GateOrderedMatrixRepresentations" | list of ordered matrix representations for each QuantumDiscreteOperator or QuantumMeasurementOperator in the circuit, assuming an input state containing Max[Max/@orders] qudits (subsystems) |
| {"GateOrderedMatrixRepresentations",n} | list of ordered matrix representations for each QuantumDiscreteOperator or QuantumMeasurementOperator in the circuit, assuming an input state containing n qudits (subsystems) |
| "GateArities" | list of arities for each QuantumDiscreteOperator or QuantumMeasurementOperator in the circuit |
| "GateDimensions" | list of qudit dimensionalities for each QuantumDiscreteOperator or QuantumMeasurementOperator in the circuit |
| "GateOrders" | list of qudit application orders for each QuantumDiscreteOperator or QuantumMeasurementOperator in the circuit |
| "Diagram" | diagrammatic representation of the circuit operator |
| "Properties" | list of all property names |
| "S" | S-gate (equivalent to a π/2 PHASE gate) |
| "T" | T-gate (equivalent to a π/4 PHASE gate) |
| "CNOT" | CNOT gate for qubits (controlled NOT - equivalent to a CX gate) |
| {"CNOT",d} | CNOT gate for d-dimensional qudits |
| "CPHASE" | CPHASE gate for qubits (controlled π PHASE gate) |
| {"CPHASE",d} | CPHASE gate for d-dimensional qudits |
| "CX" | CX gate for qubits (controlled Pauli-X gate - equivalent to a CNOT gate) |
| {"CX",d} | CX gate for d-dimensional qudits |
| "CY" | CY gate for qubits (controlled Pauli-Y gate) |
| "CZ" | CZ gate for qubits (controlled Pauli-Z gate) |
| {"CZ",d} | CZ gate for d-dimensional qudits |
| "Fourier" | QFT gate for qubits (quantum Fourier transform) |
| {"Fourier",d} | QFT gate for d-dimensional qudits |
| "InverseFourier" | IQFT gate for qubits (inverse quantum Fourier transform) |
| {"InverseFourier",d} | IQFT gate for d-dimensional qudits |
| "SWAP" | SWAP gate for qubits (swap two qubits) |
| {"SWAP",d} | SWAP gate for d-dimensional qudits |
| "RootSWAP" | square root of the SWAP gate for qubits (half swap two qubits) |
| {"RootSWAP",d} | square root of the SWAP gate for d-dimensional qudits |
| "SUM" | SUM gate for qubits (half-adder for qubits - equivalent to a CNOT gate) |
| {"SUM",d} | SUM gate for d-dimensional qudits |
| "PauliX" | Pauli-X gate for qubits (equivalent to a π rotation around the x axis of the Bloch sphere) |
| {"PauliX",d} | Pauli-X gate for d-dimensional qudits |
| "PauliY" | Pauli-Y gate for qubits (equivalent to a π rotation around the y axis of the Bloch sphere) |
| "PauliZ" | Pauli-Z gate for qubits (equivalent to a π rotation around the z axis of the Bloch sphere) |
| {"PauliZ",d} | Pauli-Z gate for d-dimensional qudits |
| "RootNOT" | square root of the Pauli-X gate for qubits (half NOT operation on one qubit) |
| {"RootNOT",d} | square root of the Pauli-X gate for d-dimensional qudits |
| "Hadamard" | Hadamard gate for qubits (equivalent to a QFT gate on one qubit) |
| "Toffoli" | Toffoli gate on 3 qubits (equivalent to a π/2 Deutsch gate) |
| {"Toffoli",n} | Toffoli gate on n qubits |
| "CSWAP" | controlled SWAP gate for qubits (Fredkin gate) |
| "PauliX" | measurement operator based on the Pauli-X gate for qubits (equivalent to a π rotation around the x axis of the Bloch sphere) |
| {"PauliX",d} | measurement operator based on the Pauli-X gate for d-dimensional qudits (not Hermitian for general d>2) |
| "PauliY" | measurement operator based on the Pauli-Y gate for qubits (equivalent to a π rotation around the y axis of the Bloch sphere) |
| "PauliZ" | measurement operator based on the Pauli-Z gate for qubits (equivalent to a π rotation around the z axis of the Bloch sphere) |
| {"PauliZ",d} | measurement operator based on the Pauli-Z gate for d-dimensional qudits (not Hermitian for general d>2) |
| "Hadamard" | measurement operator based on the Hadamard gate for qubits (equivalent to a QFT gate on one qubit) |
| "ComputationalBasis" | measurement in the 2-dimensional computational basis |
| {"ComputationalBasis",d} | measurement in the d-dimensional computational basis |
| {"ComputationalBasis",d,eigs} | measurement in the d-dimensional computational basis with eigenvalues (i.e. measurement outcomes) eigs |
| "BellBasis" | measurement in the Bell basis |
| {"BellBasis",eigs} | measurement in the Bell basis with eigenvalues (i.e. measurement outcomes) eigs |
| "PauliBasis" | measurement in the basis of Pauli matrices |
| {"PauliBasis",eigs} | measurement in the basis of Pauli matrices with eigenvalues (i.e. measurement outcomes) eigs |
| "FourierBasis" | measurement in the 2-dimensional basis of the quantum Fourier transform |
| {"FourierBasis",d} | measurement in the d-dimensional basis of the quantum Fourier transform |
| {"FourierBasis",d,eigs} | measurement in the d-dimensional basis of the quantum Fourier transform with eigenvalues (i.e. measurement outcomes) eigs |
Create a discrete quantum circuit operator in the computational basis consisting of a Hadamard gate and a Pauli-Z gate applied in series:
| In[1]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["Hadamard", {1}], ResourceFunction["QuantumDiscreteOperator"]["PauliZ", {1}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/1e0a2c83b1859548.png) |
| Out[1]= |
Show the diagrammatic representation:
| In[2]:= |
| Out[2]= |  |
| In[3]:= |
| Out[3]= |
Apply the circuit operator to the first qubit (default) of a two-qubit discrete quantum state in the computational basis:
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= |
Apply the circuit operator to the second qubit of the state instead:
| In[6]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["Hadamard", {1}], ResourceFunction["QuantumDiscreteOperator"]["PauliZ", {1}]}, {2}]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/07257722bb1b2e4b.png) |
| Out[6]= |
| In[7]:= |
| Out[7]= |
Apply the Hadamard and Pauli-Z gates in parallel to qubits 1 and 2 instead:
| In[8]:= | ![circuit3 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["Hadamard", {1}], ResourceFunction["QuantumDiscreteOperator"]["PauliZ", {2}]}]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/59f3b1d68c61836b.png) |
| Out[8]= |
| In[9]:= |
| Out[9]= | 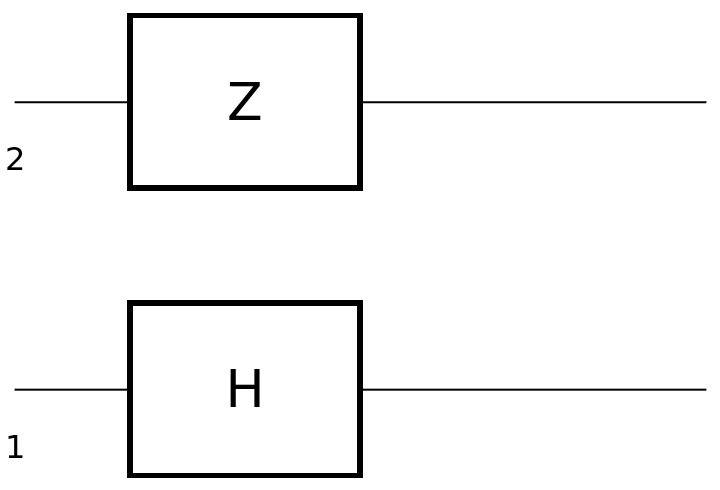 |
| In[10]:= |
| Out[10]= |
Create a discrete quantum circuit operator in the computational basis consisting of a CNOT gate with control qubit 2 and "active" qubit 3, followed by a SWAP gate for qubits 1 and 3, followed by a quantum Fourier transform gate for qubits 1, 2 and 3:
| In[11]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["CNOT", {2, 3}], ResourceFunction["QuantumDiscreteOperator"]["SWAP", {1, 3}], ResourceFunction["QuantumDiscreteOperator"][
"Fourier", {1, 2, 3}]}];
circuit["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/3fdda8f1f5969b20.png) |
| Out[12]= | 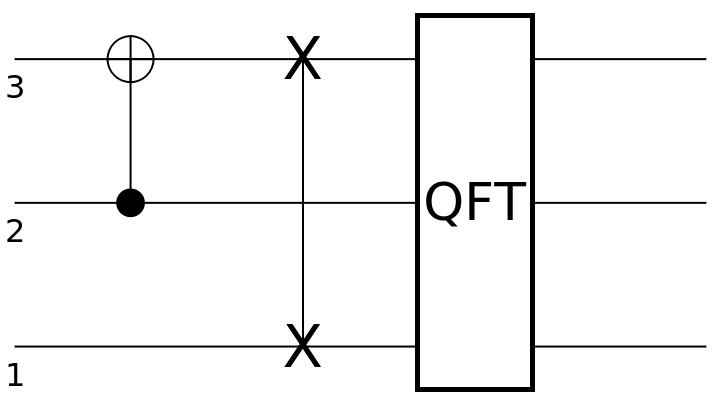 |
Return its matrix representation:
| In[13]:= |
| Out[13]= |  |
Return the ordered matrix representation (assuming a state of size 4):
| In[14]:= |
| Out[14]= |  |
| In[15]:= |
| Out[15]= |
| In[16]:= |
| Out[16]= |
| In[17]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["CNOT", {3, 2}], ResourceFunction["QuantumDiscreteOperator"]["SWAP", {1, 3}], ResourceFunction["QuantumDiscreteOperator"][
"Fourier", {1, 2, 3}]}];
circuit2["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/65ab225acd568d23.png) |
| Out[18]= | 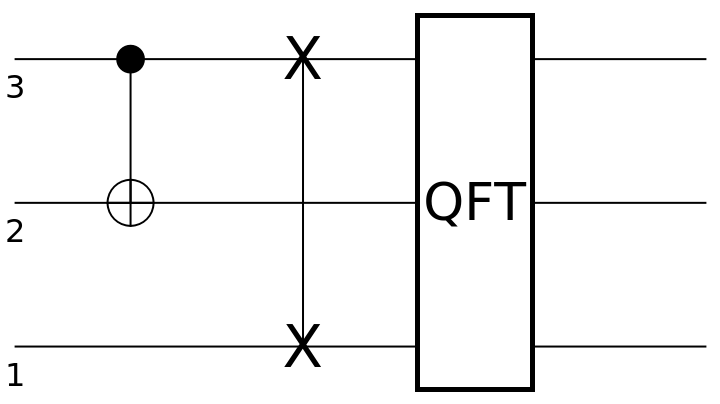 |
Return the new ordered matrix representation (assuming a state of size 4):
| In[19]:= |
| Out[19]= |  |
Create a discrete quantum circuit operator in the computational basis consisting of an inverse quantum Fourier transform gate for qubits 1 and 2, followed by a computational basis measurement gate for qubit 2:
| In[20]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["InverseFourier", {1, 2}], ResourceFunction["QuantumMeasurementOperator"][
"ComputationalBasis", {2}]}];
circuit["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/1c1fb4a7590d6c9a.png) |
| Out[21]= | 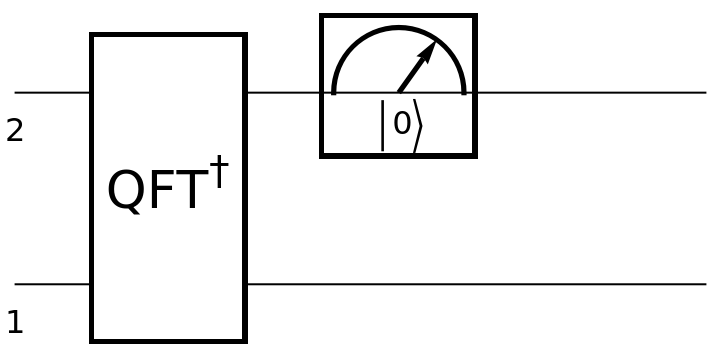 |
| In[22]:= |
| Out[23]= |
By default, all discrete quantum circuit operators are created in the Schrodinger picture:
| In[24]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["RandomUnitary"]}];
circuit["Picture"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/7dc820e1c58c32db.png) |
| Out[25]= |
Circuit operators in the Schrodinger picture can be applied to QuanumDiscreteState objects:
| In[26]:= |
| Out[27]= |
However, they cannot be applied to other operators (i.e. QuantumDiscreteOperator objects, QuantumMeasurementOperator objects or QuantumHamiltonianOperator objects). Doing so will return unevaluated:
| In[28]:= |
| Out[29]= | 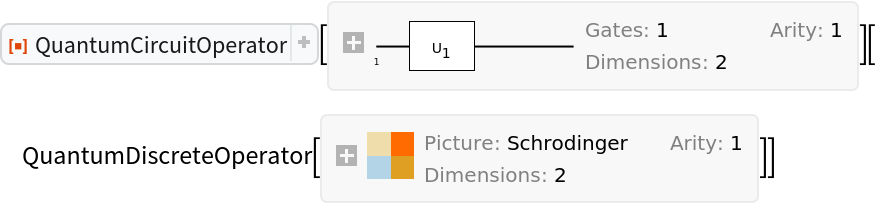 |
On the other hand, circuit operators created in the Heisenberg picture cannot be applied to QuantumDiscreteState objects (will return unevaluated):
| In[30]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["RandomUnitary"]}, "Heisenberg"];
circuit2["Picture"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/56251def380df7b1.png) |
| Out[31]= |
| In[32]:= |
| Out[32]= | 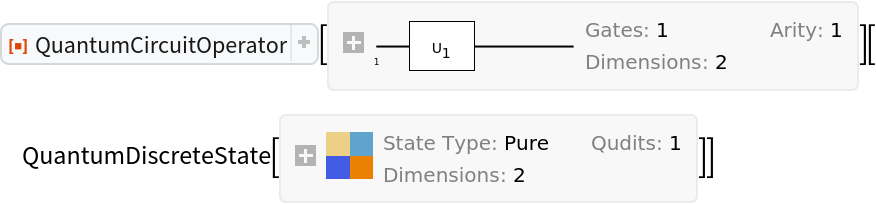 |
However, they can be applied to other operators in the Heisenberg picture (i.e. QuantumDiscreteOperator objects, QuantumMeasurementOperator objects or QuantumHamiltonianOperator objects):
| In[33]:= |
| Out[34]= |
| In[35]:= | ![measurement = ResourceFunction["QuantumMeasurementOperator"]["RandomHermitian", "Heisenberg"];
circuit2[measurement]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/02b5554fb8f3d8a7.png) |
| Out[36]= |
| In[37]:= | ![hamiltonian = ResourceFunction["QuantumHamiltonianOperator"]["RandomHermitian", "Heisenberg"];
circuit2[hamiltonian]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/5eb7cd7382d73b2d.png) |
| Out[38]= |
Apply a discrete quantum circuit operator (without measurement gates) to a QuantumMeasurement object:
| In[39]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["RandomUnitary"]}];
measurement = ResourceFunction["QuantumMeasurement"][<|Ket["up"] -> 0.7, Ket["down"] -> 0.3|>, {ResourceFunction["QuantumDiscreteState"][{1, 0}], ResourceFunction["QuantumDiscreteState"][{0, 1}]}];
result = circuit[measurement]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/34f6d93b102b30c7.png) |
| Out[40]= |
Show the resulting (evolved) states:
| In[41]:= |
| Out[41]= |  |
Apply a discrete quantum circuit operator (with measurement gates) to a QuantumMeasurement object:
| In[42]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["RandomUnitary"], ResourceFunction["QuantumMeasurementOperator"]["PauliX"]}];
result2 = circuit2[measurement]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/4cec9a5d169d9212.png) |
| Out[43]= |
Show the resulting joint distribution:
| In[44]:= |
| Out[44]= | 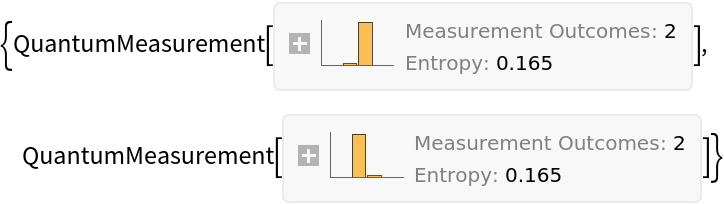 |
Create a discrete quantum circuit operator in the computational basis (default):
| In[45]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"][{{(1 + I)/2, (I - 1)/2}, {(I - 1)/
2, (1 + I)/2}}]}];
circuit["Operator"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/56860f8b1b87b74e.png) |
| Out[46]= |
| In[47]:= |
| Out[47]= |
Transform the circuit operator to the Fourier basis:
| In[48]:= |
| Out[49]= |
| In[50]:= |
| Out[50]= |
Transform the circuit operator back to the computational basis:
| In[51]:= | ![circuit3 = ResourceFunction["QuantumCircuitOperator"][circuit2, ResourceFunction["QuantumBasis"]["Computational"]];
circuit3["Operator"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/05f05b304ff7a0bf.png) |
| Out[52]= |
| In[53]:= |
| Out[53]= |
Represent a discrete quantum circuit operator in the Heisenberg picture:
| In[54]:= |
| Out[54]= |
| In[55]:= |
| Out[55]= |
Transform the circuit to the interaction picture:
| In[56]:= |
| Out[56]= |
| In[57]:= |
| Out[57]= |
Represent a two-qubit discrete quantum circuit operator in the computational basis:
| In[58]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["RandomUnitary", {1, 2}]}];
circuit["Operator"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/1fbcb61e0369f2d8.png) |
| Out[59]= |  |
| In[60]:= |
| Out[60]= |
Represent the same circuit operator in the Pauli-X basis instead:
| In[61]:= |
| Out[62]= |  |
| In[63]:= |
| Out[63]= |
Circuit operators in the Schrodinger picture can be applied to QuantumDiscreteState objects that are also in the Schrodinger picture:
| In[64]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["RandomUnitary", {1, 2}]}, "Schrodinger"];
circuit["Picture"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/15530199aa0ff804.png) |
| Out[65]= |
| In[66]:= |
| Out[67]= |
| In[68]:= |
| Out[68]= |
However, they cannot be applied to other operators in the Schrodinger picture (returns unevaluated):
| In[69]:= |
| Out[69]= |
| In[70]:= |
| Out[70]= | 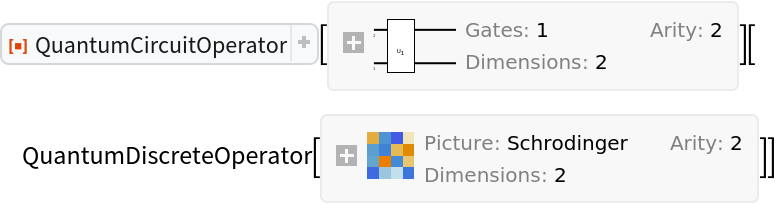 |
Likewise, circuit operators in the "PhaseSpace" picture can be applied to QuantumDiscreteState objects in the "PhaseSpace" picture:
| In[71]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["RandomUnitary", {1, 2}]}, "PhaseSpace"];
circuit2["Picture"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/57da6148d43aa2c0.png) |
| Out[72]= |
| In[73]:= |
| Out[74]= |
| In[75]:= |
| Out[75]= |
But they cannot be applied to other operators in the phase space picture (returns unevaluated):
| In[76]:= |
| Out[76]= |
| In[77]:= |
| Out[77]= |  |
On the other hand, circuit operators in the Heisenberg picture cannot be applied to QuantumDiscreteState objects in the Heisenberg picture:
| In[78]:= | ![circuit3 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["RandomUnitary", {1, 2}]}, "Heisenberg"];
circuit3["Picture"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/227fb1f160a8f43f.png) |
| Out[79]= |
| In[80]:= |
| Out[81]= |  |
But they can be applied to other operators in the Heisenberg picture:
| In[82]:= |
| Out[82]= |
| In[83]:= |
| Out[83]= |
Finally, circuit operators in the Interaction picture can be applied to both QuantumDiscreteState objects in the Interaction picture:
| In[84]:= | ![circuit4 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["RandomUnitary", {1, 2}]}, "Interaction"];
circuit4["Picture"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/26354cb8ae3af906.png) |
| Out[85]= |
| In[86]:= |
| Out[87]= |
And also to other operators in the Interaction picture:
| In[88]:= |
| Out[88]= |
| In[89]:= |
| Out[89]= |
In general, the quantum mechanical picture of a QuantumCircuitOperator and the object that it is being applied to must match.
QuantumCircuitOperator objects can be composed by application:
| In[90]:= | ![circuit1 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["CNOT", {1, 2}], ResourceFunction["QuantumDiscreteOperator"]["Hadamard", {2}]}];
circuit1["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/5cc7601a1350ad97.png) |
| Out[91]= | 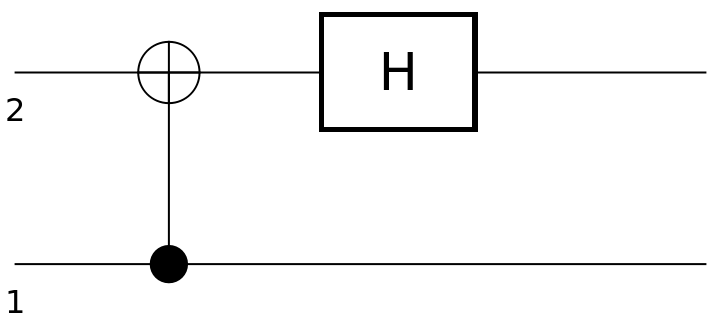 |
| In[92]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["CZ", {3, 1}], ResourceFunction["QuantumMeasurementOperator"][
"FourierBasis", {2}]}];
circuit2["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/1ca19802d62d47c2.png) |
| Out[93]= | 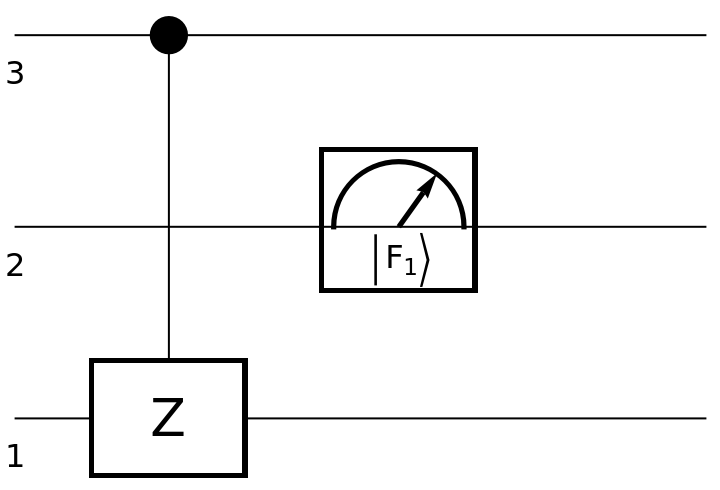 |
| In[94]:= |
| Out[95]= | 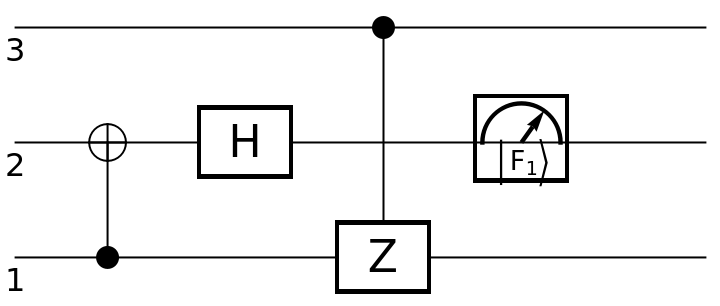 |
Circuits can also be composed by including them as "gates" in the specification of other circuits:
| In[96]:= | ![circuit4 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["S", {1}], circuit1, ResourceFunction["QuantumDiscreteOperator"]["T", {2}], circuit2}];
circuit4["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/3c4f85d7f21cea1d.png) |
| Out[97]= | 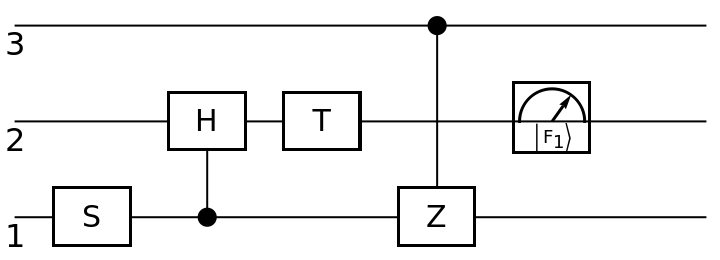 |
Show the circuit diagram for an S-gate (a π/2 phase change gate):
| In[98]:= |
| Out[99]= |  |
Show the circuit diagram for an S-gate with a control qubit:
| In[100]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"][{"ControlledU", ResourceFunction["QuantumDiscreteOperator"]["S"]}]}];
circuit2["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/025342002f9b3820.png) |
| Out[101]= | 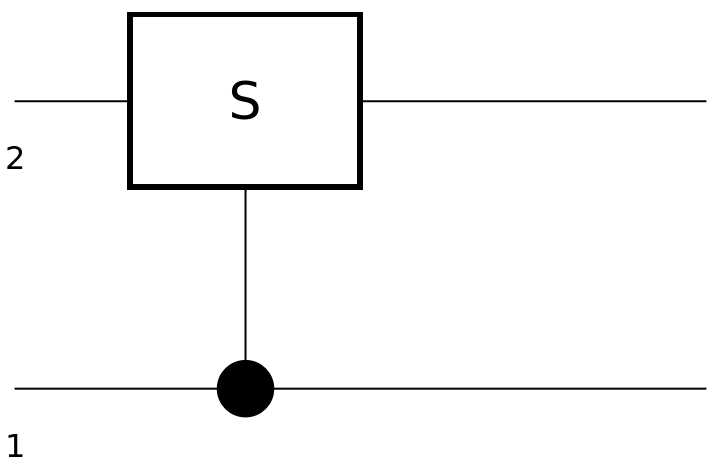 |
Show the circuit diagram for a T-gate (a π/4 phase change gate):
| In[102]:= |
| Out[103]= |  |
Show the circuit diagram for a T-gate with a control qubit:
| In[104]:= | ![circuit4 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"][{"ControlledU", ResourceFunction["QuantumDiscreteOperator"]["T"]}]}];
circuit4["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/75a01c6af8915458.png) |
| Out[105]= | 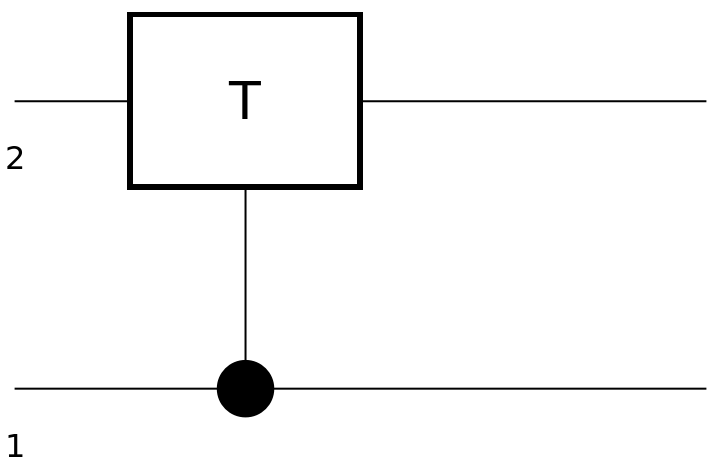 |
Show the circuit diagram for a CNOT gate (a controlled NOT gate—equivalent to a controlled Pauli-X gate):
| In[106]:= |
| Out[107]= | 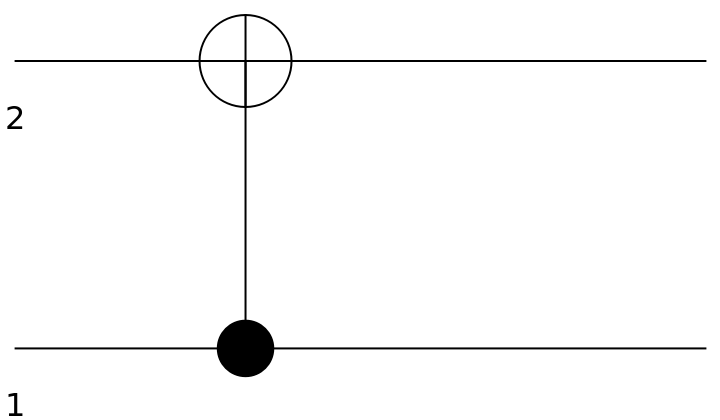 |
Show the circuit diagram for a Pauli-X gate (a π rotation around the x axis of the Bloch sphere):
| In[108]:= |
| Out[109]= |  |
Show the circuit diagram for a Pauli-Y gate (a π rotation around the y axis of the Bloch sphere):
| In[110]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["PauliY"]}];
circuit2["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/4742c0d722ce2434.png) |
| Out[111]= |  |
Show the circuit diagram for a controlled Pauli-Y gate:
| In[112]:= |
| Out[113]= | 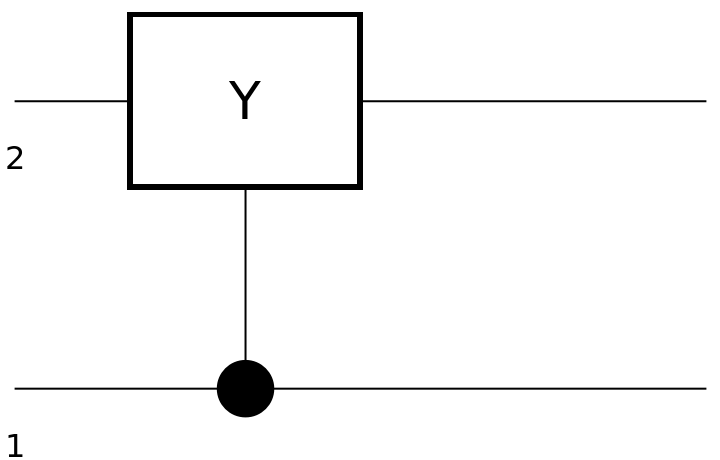 |
Show the circuit diagram for a Pauli-Z gate (a π rotation around the z axis of the Bloch sphere):
| In[114]:= | ![circuit4 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["PauliZ"]}];
circuit4["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/1e2682a4e2cc834b.png) |
| Out[115]= |  |
Show the circuit diagram for a controlled Pauli-Z gate:
| In[116]:= |
| Out[117]= | 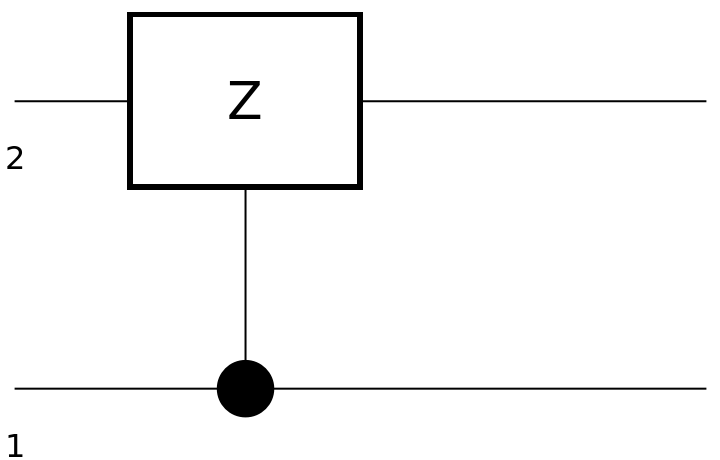 |
Show the circuit diagram for a two-qubit QFT gate (quantum Fourier transform):
| In[118]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["Fourier", {1, 2}]}];
circuit["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/0d3605916d1c6a20.png) |
| Out[119]= | 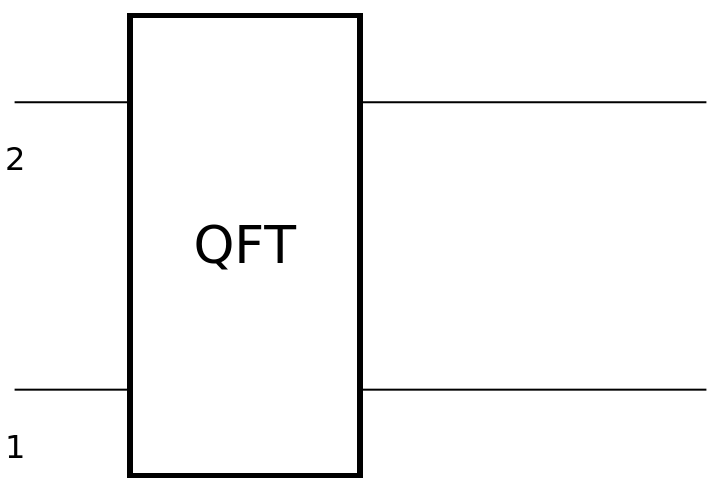 |
Show the circuit diagram for a two-qubit QFT gate with a control qubit:
| In[120]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"][{"ControlledU", ResourceFunction["QuantumDiscreteOperator"][
"Fourier", {1, 2}]}, {1, 2, 3}]}];
circuit2["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/6e1aed061d573284.png) |
| Out[121]= |  |
Show the circuit diagram for a two-qubit IQFT gate (inverse quantum Fourier transform):
| In[122]:= | ![circuit3 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["InverseFourier", {1, 2}]}];
circuit3["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/0a424d4631cafd70.png) |
| Out[123]= | 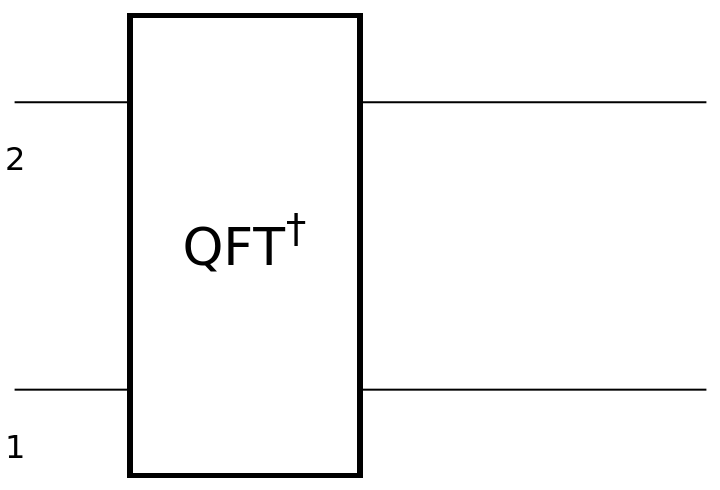 |
Show the circuit diagram for a two-qubit IQFT gate with a control qubit:
| In[124]:= | ![circuit4 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"][{"ControlledU", ResourceFunction["QuantumDiscreteOperator"][
"InverseFourier", {1, 2}]}, {1, 2, 3}]}];
circuit4["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/6f8b1ca1820f331a.png) |
| Out[125]= |  |
Show the circuit diagram for a SWAP gate:
| In[126]:= |
| Out[127]= | 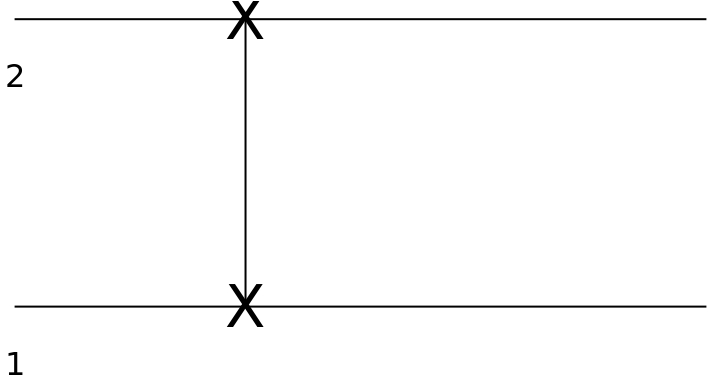 |
Show the circuit diagram for a SWAP gate with a control qubit:
| In[128]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"][{"ControlledU", ResourceFunction["QuantumDiscreteOperator"][
"SWAP", {1, 2}]}, {1, 2, 3}]}];
circuit2["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/4eab2ff108476b19.png) |
| Out[129]= | 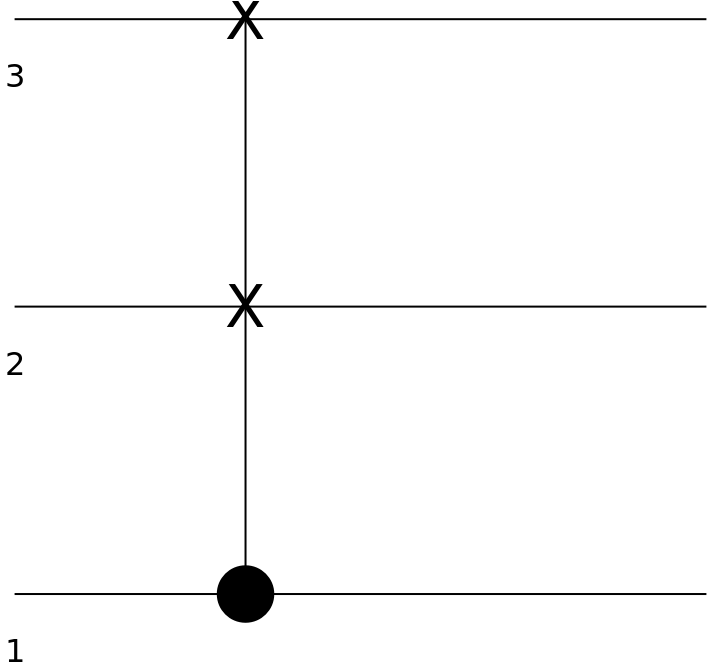 |
Show the circuit diagram for the square root of a SWAP gate (half swaps two qubits):
| In[130]:= | ![circuit3 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["RootSWAP"]}];
circuit3["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/52936597022ca48b.png) |
| Out[131]= |  |
Show the circuit diagram for the square root of a SWAP gate with a control qubit:
| In[132]:= | ![circuit4 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"][{"ControlledU", ResourceFunction["QuantumDiscreteOperator"][
"RootSWAP", {1, 2}]}, {1, 2, 3}]}];
circuit4["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/6e2ab85705ea5103.png) |
| Out[133]= | 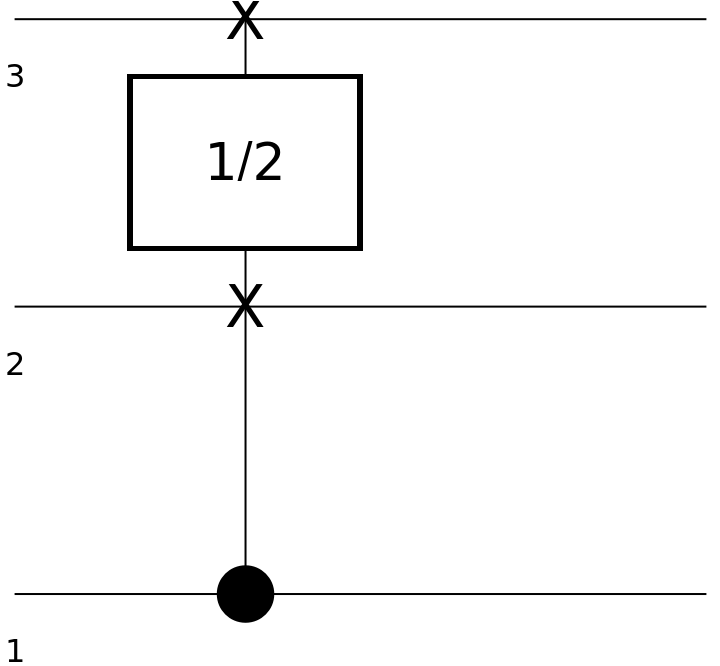 |
Show the circuit diagram for a Hadamard gate (a single-qubit quantum Fourier transform):
| In[134]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["Hadamard"]}];
circuit["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/286dbb38793c4d39.png) |
| Out[135]= |  |
Show the circuit diagram for a Hadamard gate with a control qubit:
| In[136]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"][{"ControlledU", ResourceFunction["QuantumDiscreteOperator"]["Hadamard"]}]}];
circuit2["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/26a2a22a0c01d307.png) |
| Out[137]= | 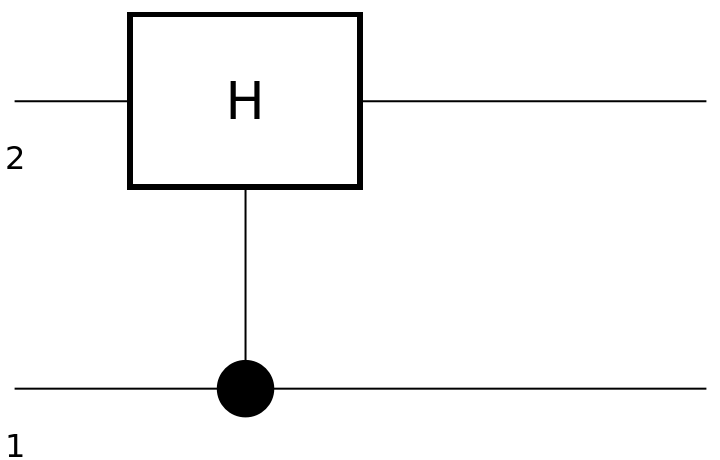 |
Show the circuit diagram for a positive operator-valued discrete quantum measurement:
| In[138]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumMeasurementOperator"][{{{1, 1 + I}, {1 - I, 2}}, {{2, 2 + I}, {2 - I, 3}}}]}];
circuit["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/0399d52570c6988d.png) |
| Out[139]= | 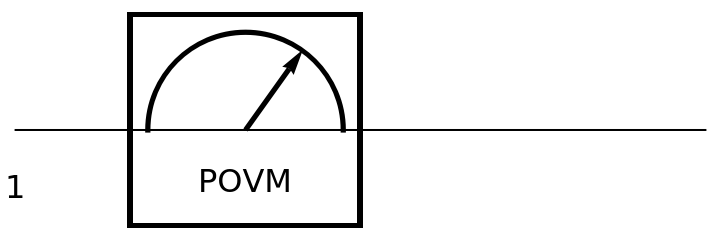 |
Show the circuit diagram for a Pauli-X measurement gate (a π rotation around the x axis of the Bloch sphere):
| In[140]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumMeasurementOperator"]["PauliX"]}];
circuit["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/0ef0f9fdd52a153e.png) |
| Out[141]= | 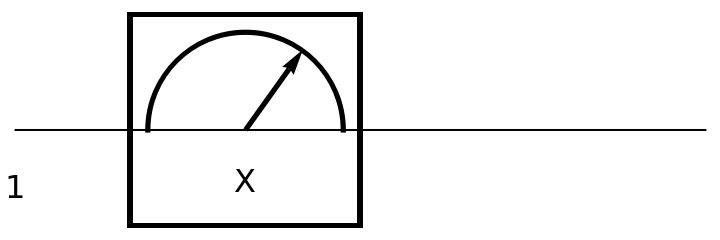 |
Show the circuit diagram for a Pauli-Y measurement gate (a π rotation around the y axis of the Bloch sphere):
| In[142]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumMeasurementOperator"]["PauliY"]}];
circuit2["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/164c9dd36786e855.png) |
| Out[143]= | 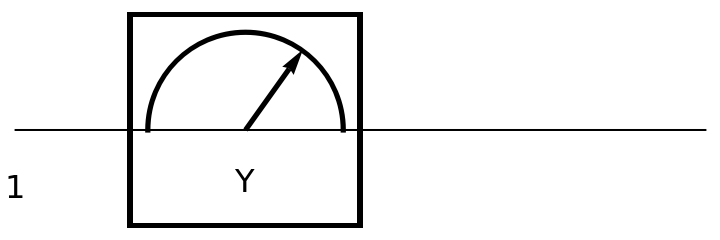 |
Show the circuit diagram for a Pauli-Z measurement gate (a π rotation around the z axis of the Bloch sphere):
| In[144]:= | ![circuit3 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumMeasurementOperator"]["PauliZ"]}];
circuit3["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/52dc39f8675e1c60.png) |
| Out[145]= | 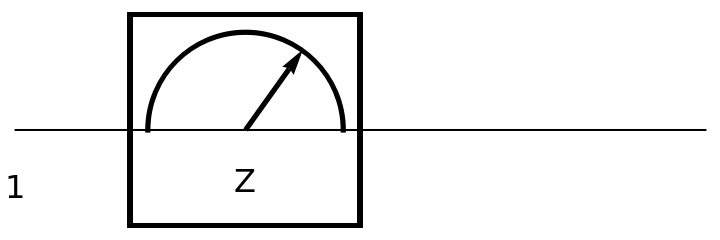 |
Show the circuit diagram for a Hadamard measurement gate (a single-qubit quantum Fourier transform):
| In[146]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumMeasurementOperator"]["Hadamard"]}];
circuit["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/6d04a5a318b887cb.png) |
| Out[147]= | 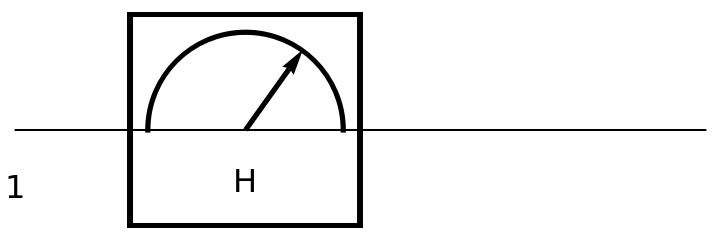 |
Show the circuit diagram for a single-qubit computational basis measurement (with default eigenvalues):
| In[148]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumMeasurementOperator"]["ComputationalBasis"]}];
circuit["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/4307f2b4e1887b63.png) |
| Out[149]= | 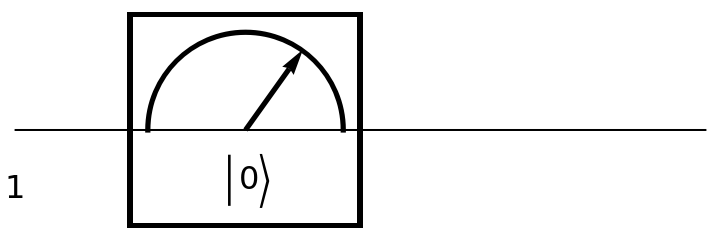 |
Show the circuit diagram for a two-qubit computational basis measurement (with default eigenvalues):
| In[150]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumMeasurementOperator"]["ComputationalBasis", {1, 2}]}];
circuit2["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/487b6645a3d0e668.png) |
| Out[151]= | 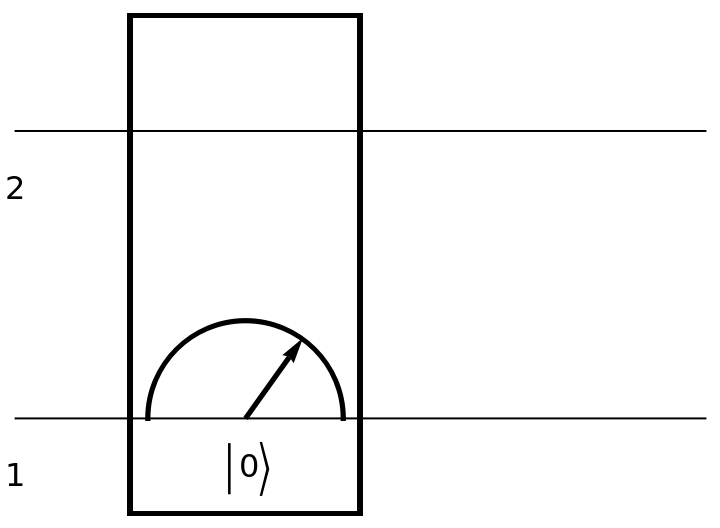 |
Show the circuit diagram for a single-qubit Bell basis measurement (with default eigenvalues):
| In[152]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumMeasurementOperator"]["BellBasis"]}];
circuit["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/2c2dcdf98764bf2e.png) |
| Out[153]= | 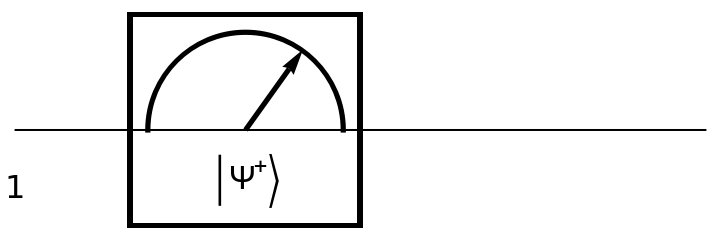 |
Show the circuit diagram for a two-qubit Bell basis measurement (with default eigenvalues):
| In[154]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumMeasurementOperator"]["BellBasis", {1, 2}]}];
circuit2["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/3514ff34f3156a9d.png) |
| Out[155]= | 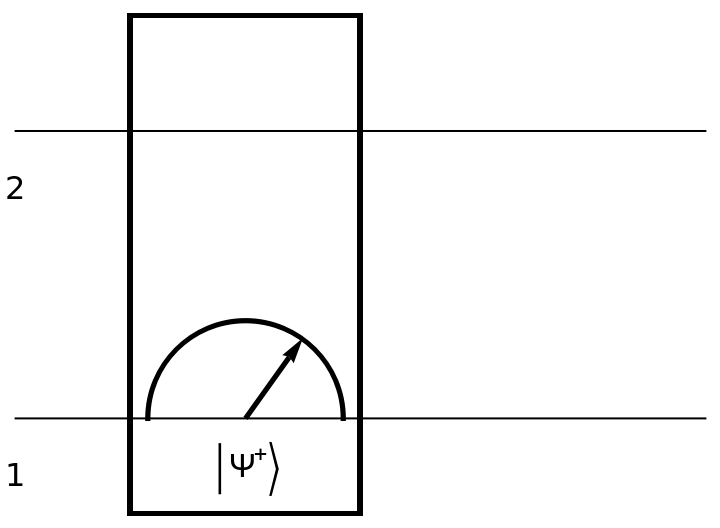 |
Show the circuit diagram for a single-qubit Fourier basis measurement:
| In[156]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumMeasurementOperator"]["FourierBasis"]}];
circuit["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/3a7e384ef530d600.png) |
| Out[157]= | 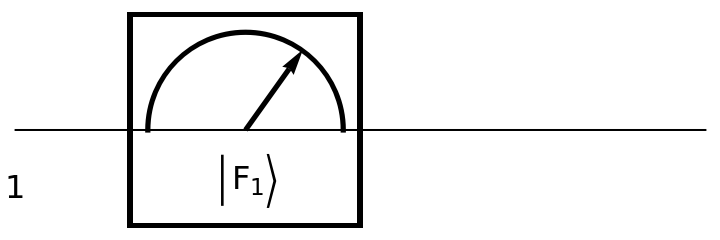 |
Show the circuit diagram for a two-qubit Fourier basis measurement:
| In[158]:= | ![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumMeasurementOperator"]["FourierBasis", {1, 2}]}];
circuit2["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/27bc8ed51a26f57a.png) |
| Out[159]= | 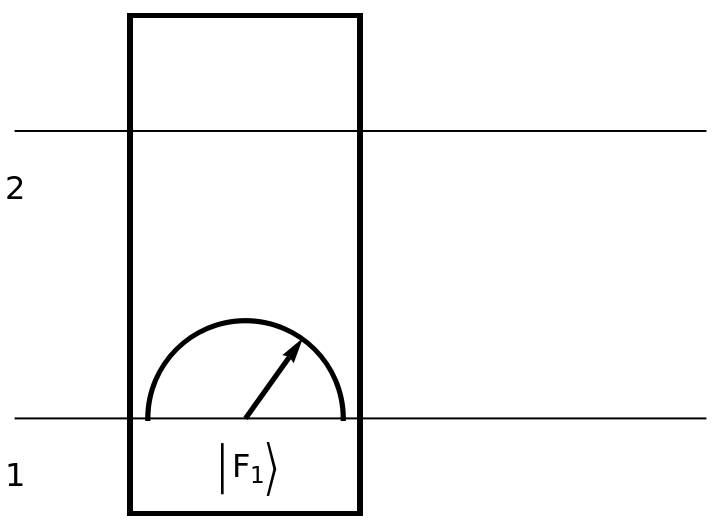 |
View a list of properties that can be extracted from a QuantumCircuitOperator object:
| In[160]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["RandomUnitary", {1}], ResourceFunction["QuantumDiscreteOperator"]["SWAP", {2, 1}]}, {2, 3}]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/1561c1ebb7eedce7.png) |
| Out[160]= |
| In[161]:= |
| Out[161]= |  |
Return the circuit operator association:
| In[162]:= |
| Out[162]= |  |
Return which QuantumBasis the circuit operator is defined with respect to:
| In[163]:= |
| Out[163]= |
Return which quantum mechanical picture the circuit operator is defined with respect to:
| In[164]:= |
| Out[164]= |
Return the association of names and basis elements:
| In[165]:= |
| Out[165]= |
Return the matrix representation:
| In[166]:= |
| Out[166]= |  |
Return the ordered matrix representation (when applied to qubits 2 and 3), assuming a state consisting of 3 qubits:
| In[167]:= |
| Out[167]= |  |
Return the ordered matrix representation (when applied to qubits 2 and 3), assuming a state consisting of 4 qubits:
| In[168]:= |
| Out[168]= |  |
Return the representation as a QuantumDiscreteOperator:
| In[169]:= |
| Out[169]= |
Return the arity (number of input subsystems):
| In[170]:= |
| Out[170]= |
Return the number of dimensions:
| In[171]:= |
| Out[171]= |
Return the order in which the circuit operator is applied to subsystems:
| In[172]:= |
| Out[172]= |
Determine whether the circuit operator is Hermitian:
| In[173]:= |
| Out[173]= |
Determine whether the circuit operator is unitary:
| In[174]:= |
| Out[174]= |
Return the list of eigenvalues:
| In[175]:= |
| Out[175]= |
Return the list of eigenvectors:
| In[176]:= |
| Out[176]= |  |
Return the list of gates in the circuit:
| In[177]:= |
| Out[177]= |  |
Return the list of operator associations for each gate:
| In[178]:= |
| Out[178]= |  |
Return the list of QuantumBasis objects for each gate:
| In[179]:= |
| Out[179]= |
Return the list of quantum mechanical pictures for each gate:
| In[180]:= |
| Out[180]= |
Return the list of associations of names and basis elements for each gate:
| In[181]:= |
| Out[181]= |
Return the list of matrix representations for each gate:
| In[182]:= |
| Out[182]= |
Return the list of ordered matrix representations for each gate, assuming a state consisting of 3 qubits:
| In[183]:= |
| Out[183]= |  |
Return the list of ordered matrix representations for each gate, assuming a state consisting of 4 qubits:
| In[184]:= |
| Out[184]= |  |
Return the list of arities (number of input subsystems) for each gate:
| In[185]:= |
| Out[185]= |
Return the list of numbers of dimensions for each gate:
| In[186]:= |
| Out[186]= |
Return the list of orders in which the gates are applied to subsystems:
| In[187]:= |
| Out[187]= |
Show the diagrammatic representation of the circuit operator:
| In[188]:= |
| Out[188]= |  |
Represent a three-qubit quantum Fourier transform as a composition of Hadamard gates, controlled S-phase and T-phase gates and a single SWAP operation at the end:
| In[189]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["Hadamard", {1}], ResourceFunction["QuantumDiscreteOperator"][{"ControlledU", ResourceFunction["QuantumDiscreteOperator"]["S"]}, {2, 1}], ResourceFunction["QuantumDiscreteOperator"][{"ControlledU", ResourceFunction["QuantumDiscreteOperator"]["T"]}, {3, 1}], ResourceFunction["QuantumDiscreteOperator"][{"ControlledU", ResourceFunction["QuantumDiscreteOperator"]["T"]}, {3, 1}], ResourceFunction["QuantumDiscreteOperator"]["Hadamard", {2}], ResourceFunction["QuantumDiscreteOperator"][{"ControlledU", ResourceFunction["QuantumDiscreteOperator"]["S"]}, {3, 2}], ResourceFunction["QuantumDiscreteOperator"]["Hadamard", {3}], ResourceFunction["QuantumDiscreteOperator"]["SWAP", {1, 3}]}];
circuit["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/15f437b00a866e3b.png) |
| Out[190]= | 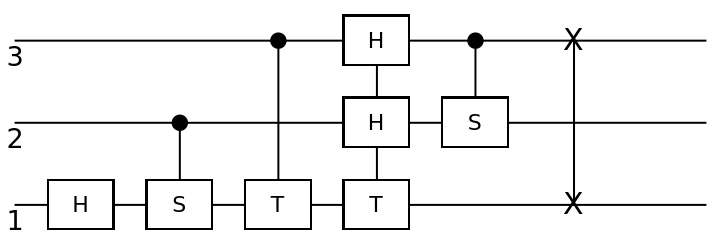 |
Apply the circuit operator to a random three-qubit discrete quantum state:
| In[191]:= |
| Out[192]= |
Compare the matrix representation of the circuit operator to the matrix representation of the standard three-qubit quantum Fourier transform:
| In[193]:= |
| Out[193]= |
Compare the effect of the standard three-qubit quantum Fourier transform on the random state from a previous example:
| In[194]:= |
| Out[194]= |
Represent a Hadamard test circuit (for creating a random variable whose expected value is the expected real part of the observed value of a quantum state with respect to some unitary operator):
| In[195]:= | ![operator = ResourceFunction["QuantumDiscreteOperator"]["RandomUnitary", {1, 2}];
circuit = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["Hadamard", {1}], ResourceFunction["QuantumDiscreteOperator"][{"ControlledU", operator}, {1, 2, 3}], ResourceFunction["QuantumDiscreteOperator"]["Hadamard", {1}], ResourceFunction["QuantumMeasurementOperator"]["PauliZ", {1}]}];
circuit["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/09b5108c61f4326d.png) |
| Out[196]= |  |
Apply the circuit operator to a random three-qubit discrete quantum state:
| In[197]:= |
| Out[198]= |
Represent a quantum parity check circuit (for determining the expected number of 1s in an arbitrary string of qubits), shown here for the three-qubit case:
| In[199]:= | ![circuit = ResourceFunction[
"QuantumCircuitOperator"][{Append[
ResourceFunction["QuantumDiscreteOperator"]["CNOT", {#, 4}] & /@ Range[3], ResourceFunction["QuantumMeasurementOperator"][
"ComputationalBasis", {4}]]}];
circuit["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/79d/79d84f14-cc50-448a-a2b9-1c6f51fb38f0/1b74e66c166e7b3d.png) |
| Out[200]= | 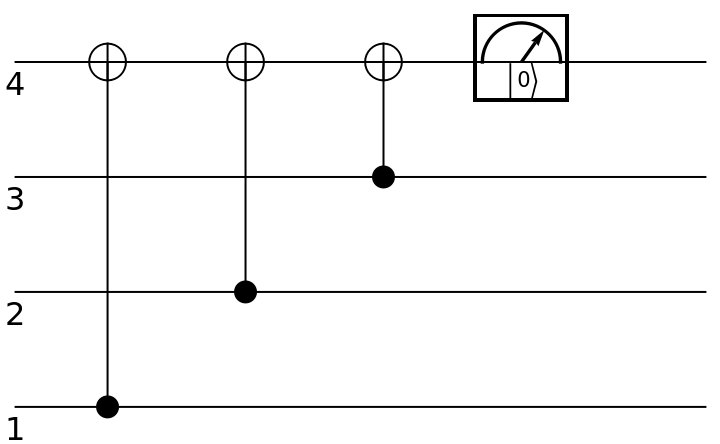 |
Apply the circuit operator to a random four-qubit discrete quantum state:
| In[201]:= |
| Out[202]= |
This work is licensed under a Creative Commons Attribution 4.0 International License