Basic Examples (3)
Compute the tensor product of a single-qubit Pauli-X QuantumBasis object and a single-qubit Pauli-Z QuantumBasis object to obtain a two-qubit QuantumBasis object:
Show the product basis:
Compute the tensor product of a two-qubit Pauli-X QuantumBasis object and a three-qubit Pauli-Z QuantumBasis object to obtain a five-qubit QuantumBasis object instead:
Scope (9)
Compute the tensor product of two pure QuantumDiscreteState objects to obtain another pure QuantumDiscreteState object:
Check that this is a pure state:
Compute the tensor product of two mixed QuantumDiscreteState objects to obtain another mixed QuantumDiscreteState object:
Compute the tensor product of a pure QuantumDiscreteState object and a mixed QuantumDiscreteState object to obtain a mixed QuantumDiscreteState object:
Compute the tensor product of an arity-2 QuantumDiscreteOperator object and an arity-1 QuantumDiscreteOperator object to obtain an arity-3 QuantumDiscreteOperator object:
Compute the tensor product of two arity-2 projection-valued QuantumMeasurementOperator objects to obtain an arity-4 projection-valued QuantumMeasurementOperator object:
Compute the tensor product of two arity-1 positive operator-valued QuantumMeasurementOperator objects to obtain an arity-2 positive operator-valued QuantumMeasurementOperator object:
Compute the tensor product of two arity-1 QuantumHamiltonianOperator objects to obtain an arity-2 QuantumHamiltonianOperator object:
Compute the tensor product of two arity-2 QuantumCircuitOperator objects to obtain an arity-4 QuantumDiscreteOperator object:
Show the matrix representation of the resulting operator:
Compute the tensor product of a list of quantum objects:
Compute the tensor product of higher-dimensional quantum objects:
When taking a tensor product of QuantumDiscreteState, QuantumDiscreteOperator, QuantumMeasurementOperator, QuantumHamiltonianOperator or QuantumCircuitOperator objects, QuantumTensorProduct will also compute the tensor product of the associated QuantumBasis objects implicitly:
The resulting basis is equivalent to the tensor product of the two constituent bases:
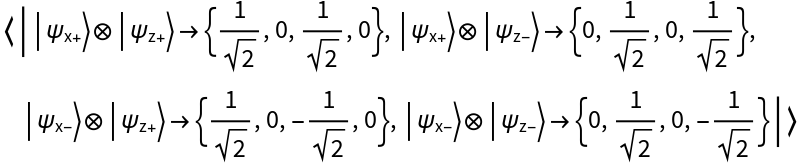
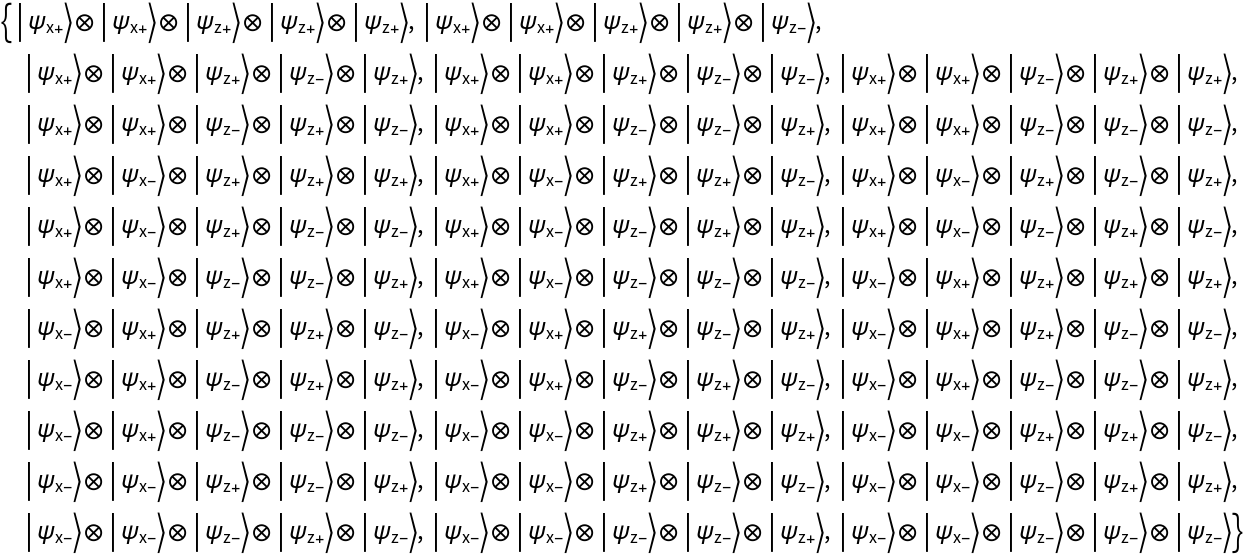
![state = ResourceFunction["QuantumTensorProduct"][
ResourceFunction["QuantumDiscreteState"][{1 + I, 1 - I}], ResourceFunction["QuantumDiscreteState"][{1/Sqrt[2], 0, 0, 1/Sqrt[2]}]];
state["Amplitudes"]](https://www.wolframcloud.com/obj/resourcesystem/images/0b4/0b4fadf6-f109-4087-a3be-67677e8c9753/7687657eca3b1d23.png)
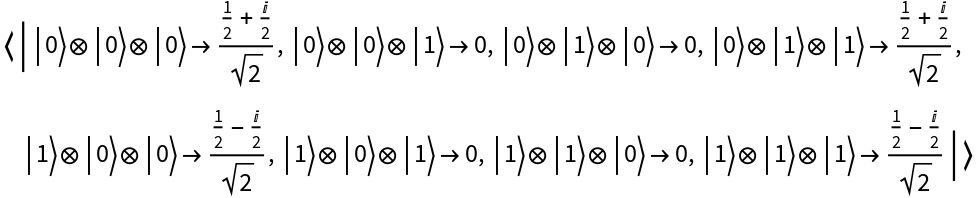
![state2 = ResourceFunction["QuantumTensorProduct"][
ResourceFunction[
"QuantumDiscreteState"][{{1/4 + I, 1/2}, {1/2, 3/4 - I}}], ResourceFunction["QuantumDiscreteState"][{{1 + I, 0}, {0, I - 1}}]];
state2["Amplitudes"]](https://www.wolframcloud.com/obj/resourcesystem/images/0b4/0b4fadf6-f109-4087-a3be-67677e8c9753/67857f25660c0426.png)
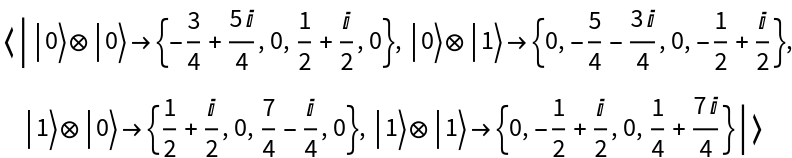
![state3 = ResourceFunction["QuantumTensorProduct"][
ResourceFunction[
"QuantumDiscreteState"][{{1/4 + I, 1/2}, {1/2, 3/4 - I}}], ResourceFunction["QuantumDiscreteState"][{1, -I}]];
state3["Amplitudes"]](https://www.wolframcloud.com/obj/resourcesystem/images/0b4/0b4fadf6-f109-4087-a3be-67677e8c9753/00ad0688a75d717a.png)
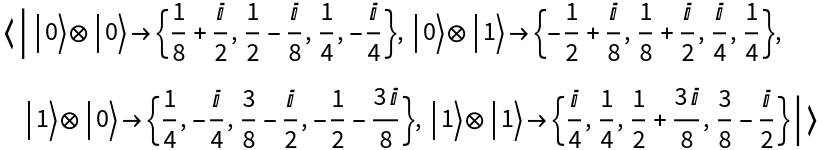
![operator = ResourceFunction["QuantumTensorProduct"][
ResourceFunction["QuantumDiscreteOperator"]["CNOT", {1, 3}], ResourceFunction["QuantumDiscreteOperator"]["Hadamard", {2}]];
operator["MatrixRepresentation"]](https://www.wolframcloud.com/obj/resourcesystem/images/0b4/0b4fadf6-f109-4087-a3be-67677e8c9753/7d106357e1569804.png)
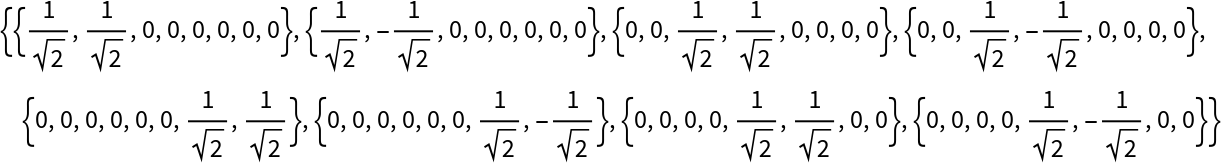
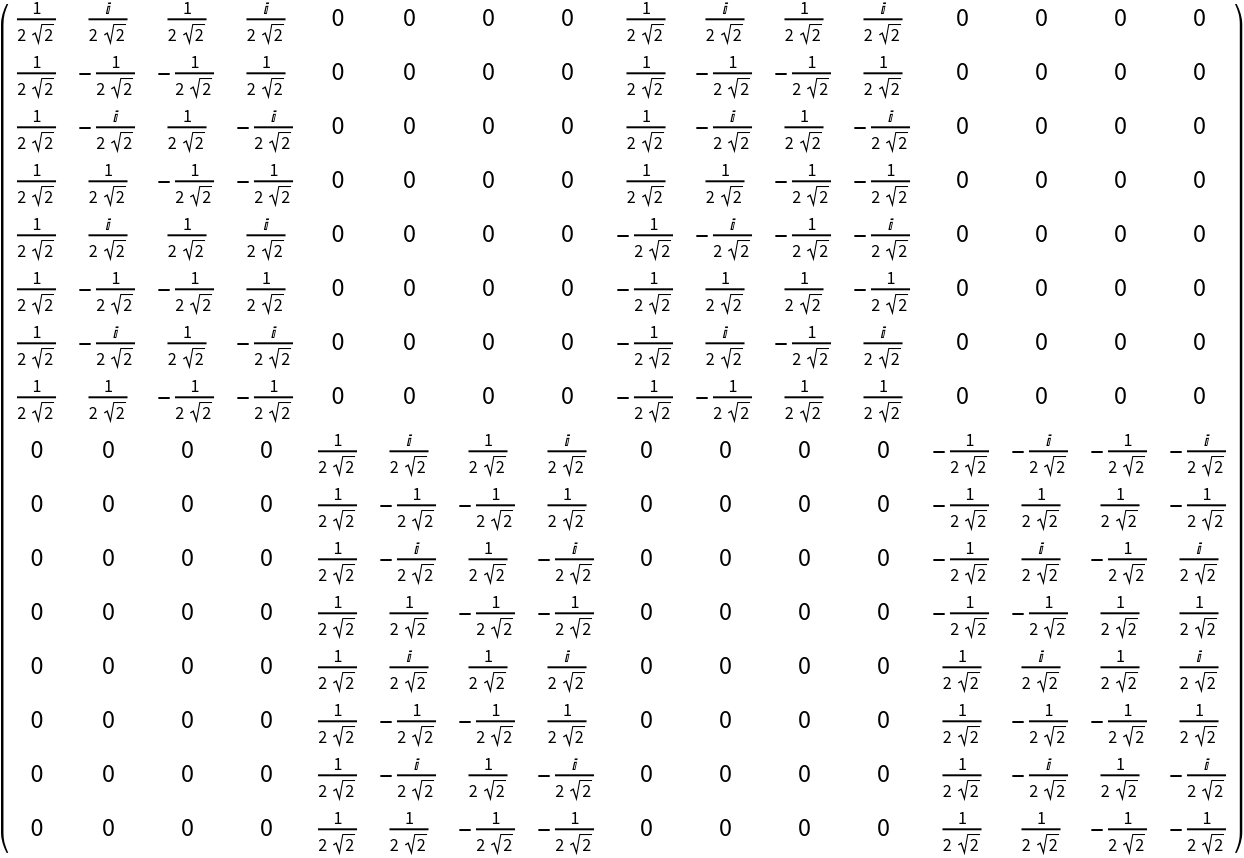
![measurement = ResourceFunction["QuantumTensorProduct"][
ResourceFunction["QuantumMeasurementOperator"][
"ComputationalBasis", {2, 4}], ResourceFunction["QuantumMeasurementOperator"][
"FourierBasis", {1, 3}]];
measurement["MatrixRepresentation"]](https://www.wolframcloud.com/obj/resourcesystem/images/0b4/0b4fadf6-f109-4087-a3be-67677e8c9753/14dcaecef57f7b00.png)
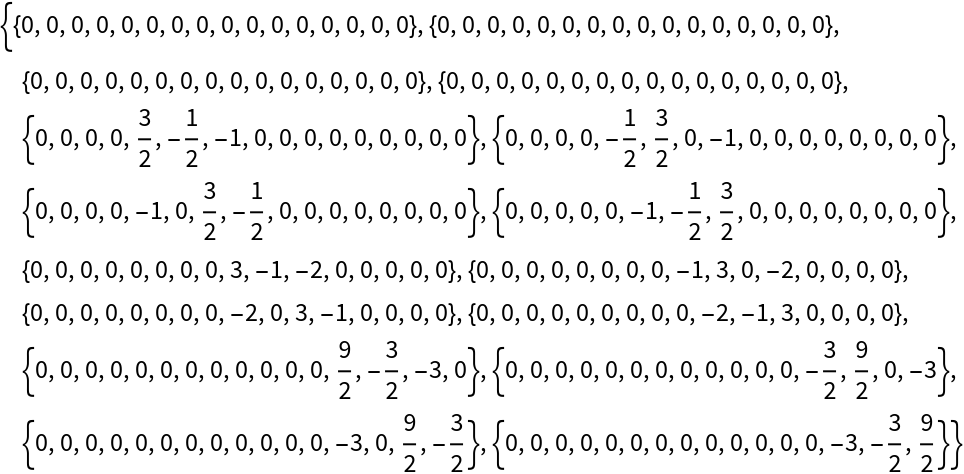
![measurement2 = ResourceFunction["QuantumTensorProduct"][
ResourceFunction[
"QuantumMeasurementOperator"][{{{0, 0}, {0, 1}}, {{1, -1}, {-1, 1}}}], ResourceFunction[
"QuantumMeasurementOperator"][{{{1, -1}, {-1, 1}}, {{0, 1}, {1, 0}}}]];
measurement2["POVMElements"]](https://www.wolframcloud.com/obj/resourcesystem/images/0b4/0b4fadf6-f109-4087-a3be-67677e8c9753/6cad1bfb93084b95.png)
![hamiltonian = ResourceFunction["QuantumTensorProduct"][
ResourceFunction[
"QuantumHamiltonianOperator"][{{1 + \[FormalT]^2, 1 - \[FormalT]^2}, {1 - \[FormalT]^2, 1 + \[FormalT]^2}}], ResourceFunction["QuantumHamiltonianOperator"]["PauliX"]];
hamiltonian["Operator"]](https://www.wolframcloud.com/obj/resourcesystem/images/0b4/0b4fadf6-f109-4087-a3be-67677e8c9753/24bcb410fd1743c9.png)
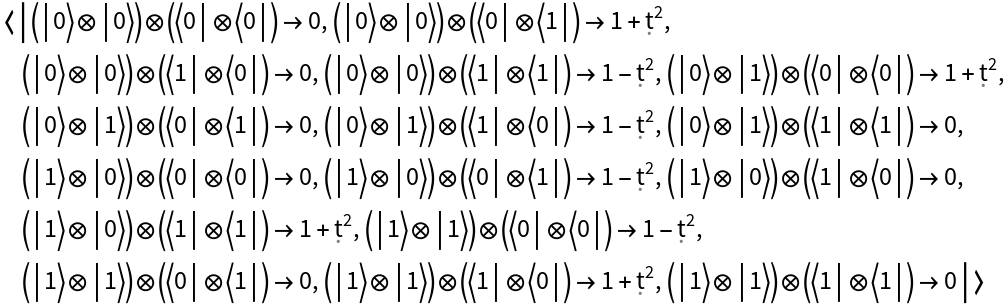
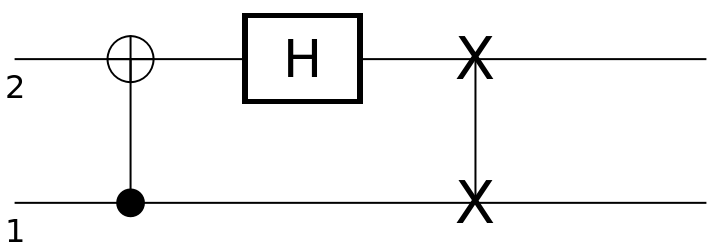
![circuit1 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["CNOT", {1, 2}], ResourceFunction["QuantumDiscreteOperator"]["Hadamard", {2}], ResourceFunction["QuantumDiscreteOperator"]["SWAP", {1, 2}]}, {1, 2}];
circuit1["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/0b4/0b4fadf6-f109-4087-a3be-67677e8c9753/5d8fd756242a23d0.png)
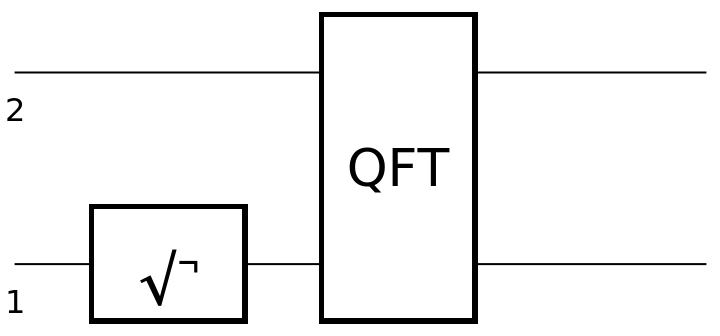
![circuit2 = ResourceFunction[
"QuantumCircuitOperator"][{ResourceFunction[
"QuantumDiscreteOperator"]["RootNOT", {1}], ResourceFunction["QuantumDiscreteOperator"][
"Fourier", {1, 2}]}, {3, 4}];
circuit2["Diagram"]](https://www.wolframcloud.com/obj/resourcesystem/images/0b4/0b4fadf6-f109-4087-a3be-67677e8c9753/1b30101595b036b5.png)
![state = ResourceFunction[
"QuantumTensorProduct"][{ResourceFunction[
"QuantumDiscreteState"][{I, -1}], ResourceFunction["QuantumDiscreteState"][{-I, 1}], ResourceFunction[
"QuantumDiscreteState"][{1/Sqrt[2], -1/Sqrt[2]}]}];
state["Amplitudes"]](https://www.wolframcloud.com/obj/resourcesystem/images/0b4/0b4fadf6-f109-4087-a3be-67677e8c9753/66ad56f2cfcff07b.png)
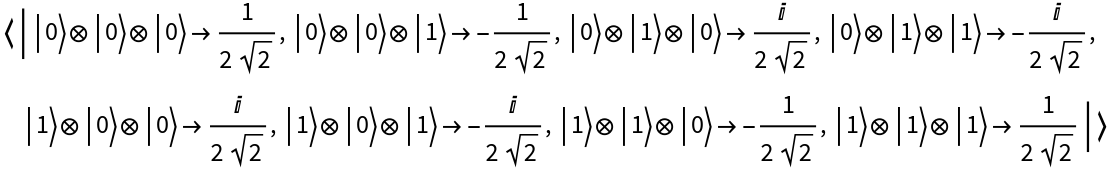
![state = ResourceFunction["QuantumTensorProduct"][
ResourceFunction["QuantumDiscreteState"][{1, 1 + I, 1 - I}, 3], ResourceFunction["QuantumDiscreteState"][{1/Sqrt[3], I, Sqrt[2/3] - I}, 3]];
state["Amplitudes"]](https://www.wolframcloud.com/obj/resourcesystem/images/0b4/0b4fadf6-f109-4087-a3be-67677e8c9753/3ecce64ec8a31320.png)
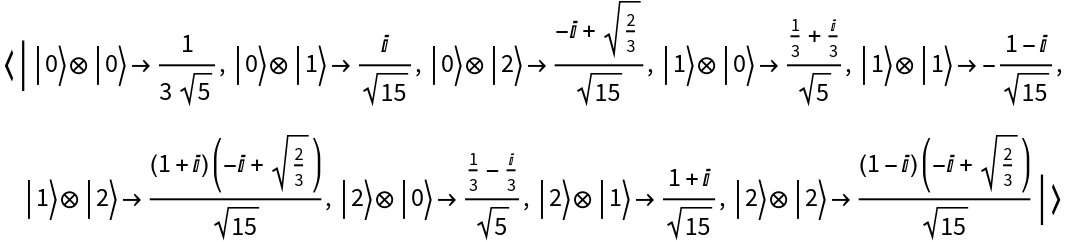
![state1 = ResourceFunction["QuantumDiscreteState"][{1 + I, 1 - I}, ResourceFunction["QuantumBasis"]["Fourier"]];
state2 = ResourceFunction["QuantumDiscreteState"][{1/Sqrt[2], -1/Sqrt[2]}, ResourceFunction["QuantumBasis"]["PauliZ"]];
newState = ResourceFunction["QuantumTensorProduct"][state1, state2];
newState["Amplitudes"]](https://www.wolframcloud.com/obj/resourcesystem/images/0b4/0b4fadf6-f109-4087-a3be-67677e8c9753/75683223d742e7e4.png)