Wolfram Language Paclet Repository
Community-contributed installable additions to the Wolfram Language
QuantumCircuitOperator |
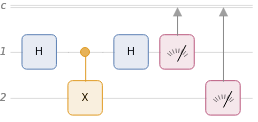
QuantumState |
Initial state | |00〉 |
After 1st Hadamard | |00〉 2 |10〉 2 |
After CNOT | |00〉 2 |11〉 2 |
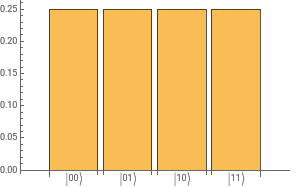
After 2nd Hadamard | |00〉 2 |01〉 2 |10〉 2 |11〉 2 |
QuantumState |
QuantumCircuitOperator |
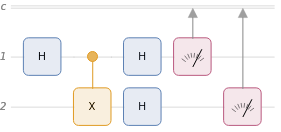
QuantumState |
Initial state | |00〉 |
After Hadamard on 1st qubit | |00〉 2 |10〉 2 |
After CNOT | |00〉 2 |11〉 2 |
After Hadamard on 1st qubit | |00〉 2 |01〉 2 |10〉 2 |11〉 2 |
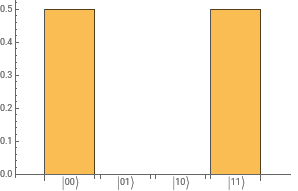
After Hadamard on 2nd qubit | |00〉 2 |11〉 2 |
QuantumState |
QuantumCircuitOperator |
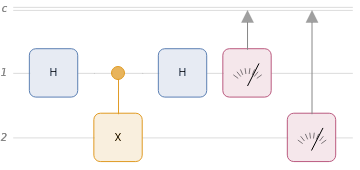
QuantumOperator |