Basic Examples (2)
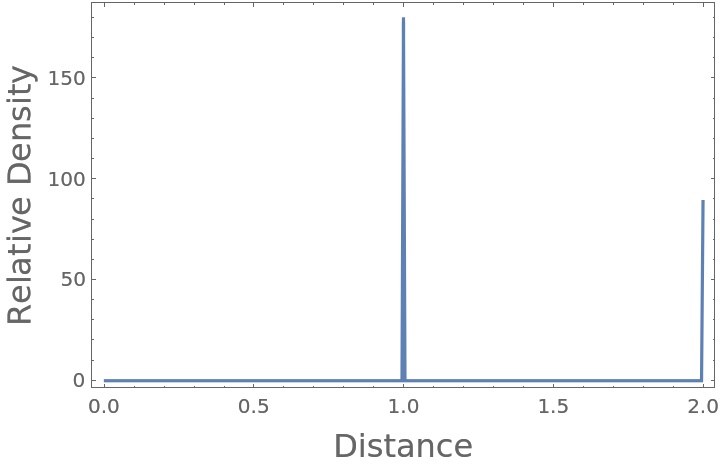
Compute the radial distribution function from two points:
Compute the radial distribution function of a set of coordinates enclosed in a periodic 1D "box" of size (L = 4):
Display the coordinates in number line format along the axis for which the positions differ:
The radial distribution function has non-zero peaks at positions near those of the exact distances apart:
Plot the radial distribution function characteristic of this system:
Options (2)
Cross-correlations can be computed using the option "ReferenceCoordinates":
Radial distribution function takes the same options as Compile, and benefits from automated compilation to C:
Applications (2)
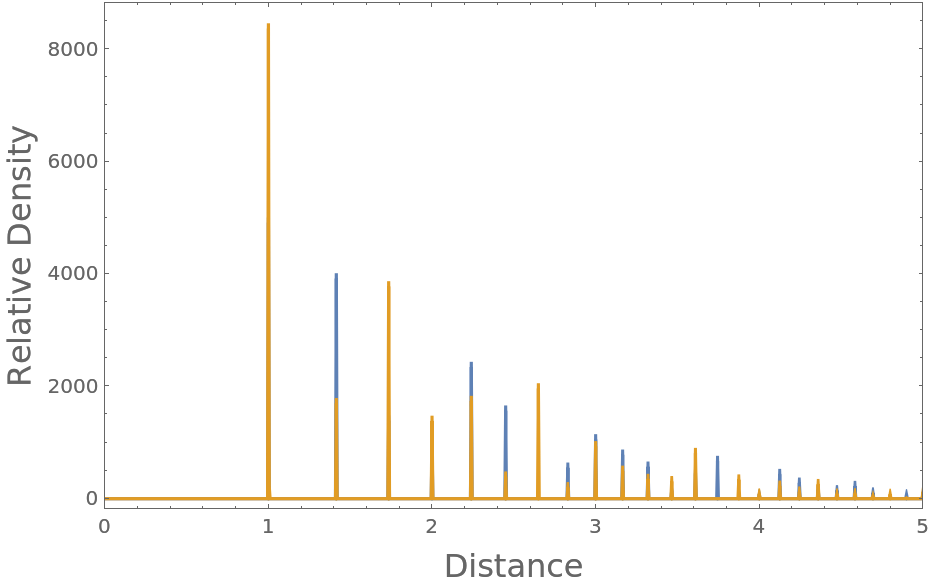
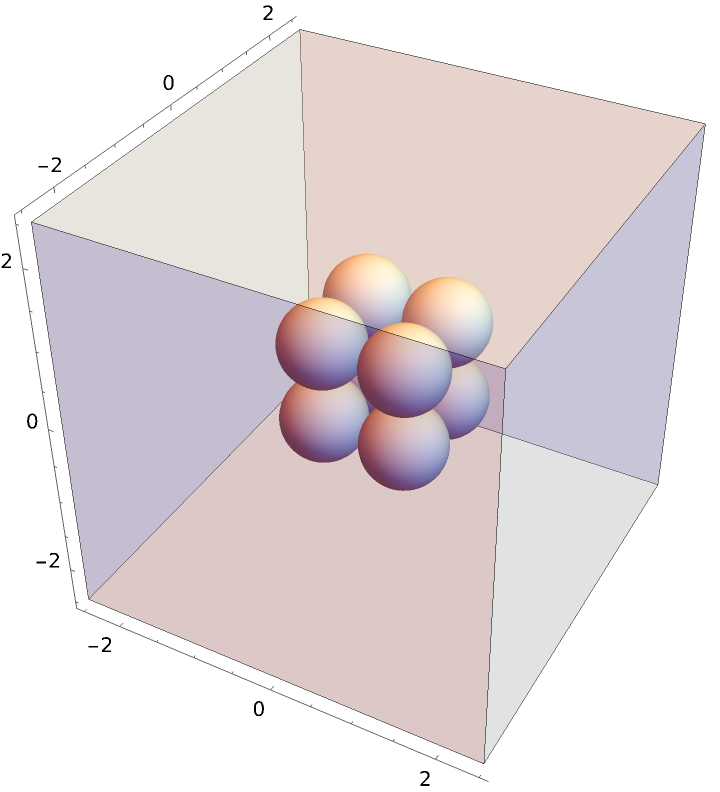
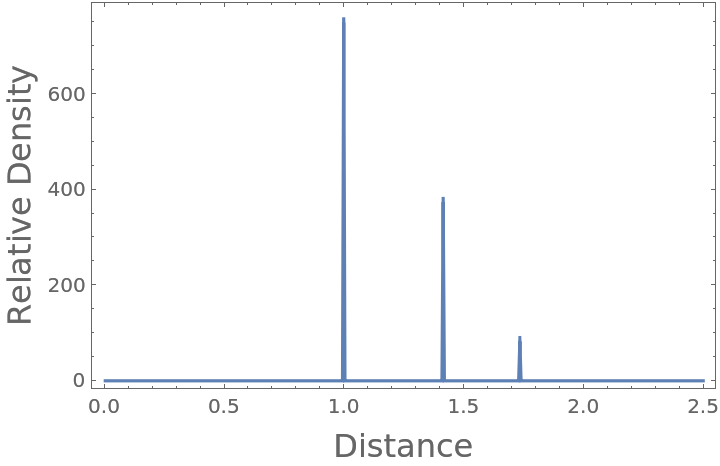
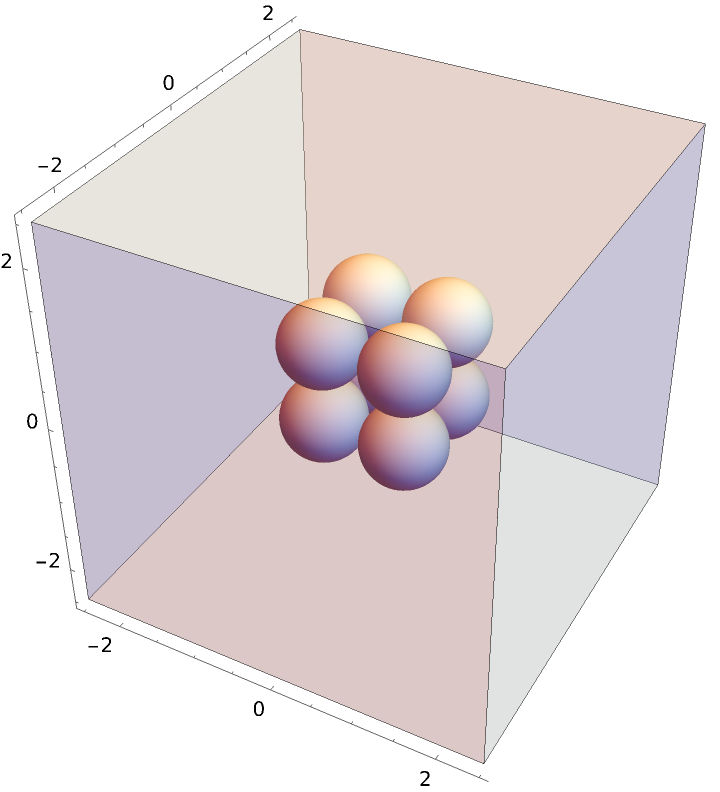
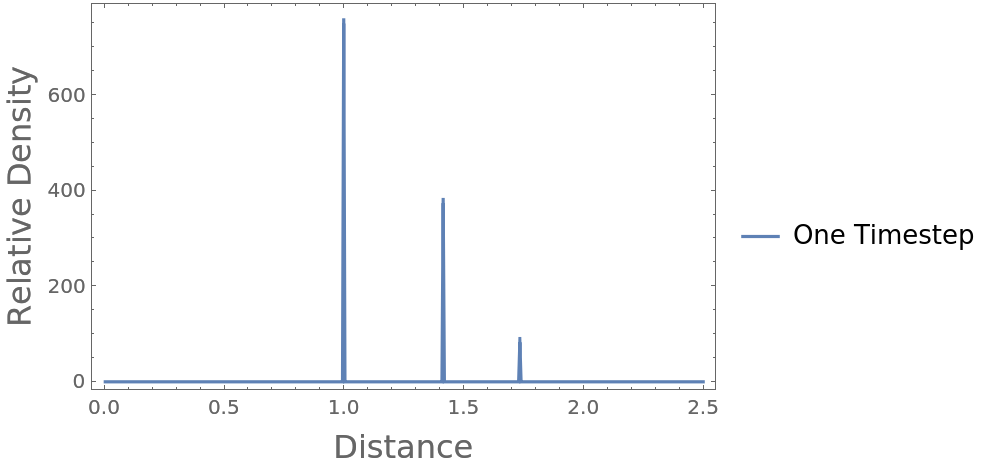
Compute the radial distribution function characteristic of a cube with unit length, enclosed in a sufficiently larger periodic box:
Plot the resulting radial distribution function, where you can see nearest neighbor, polygonal face hypotenuse, and internal hypotenuse distances:
Properties and Relations (4)
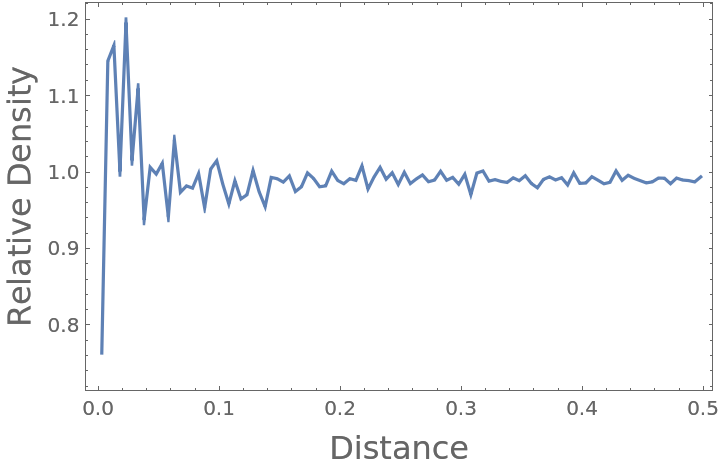
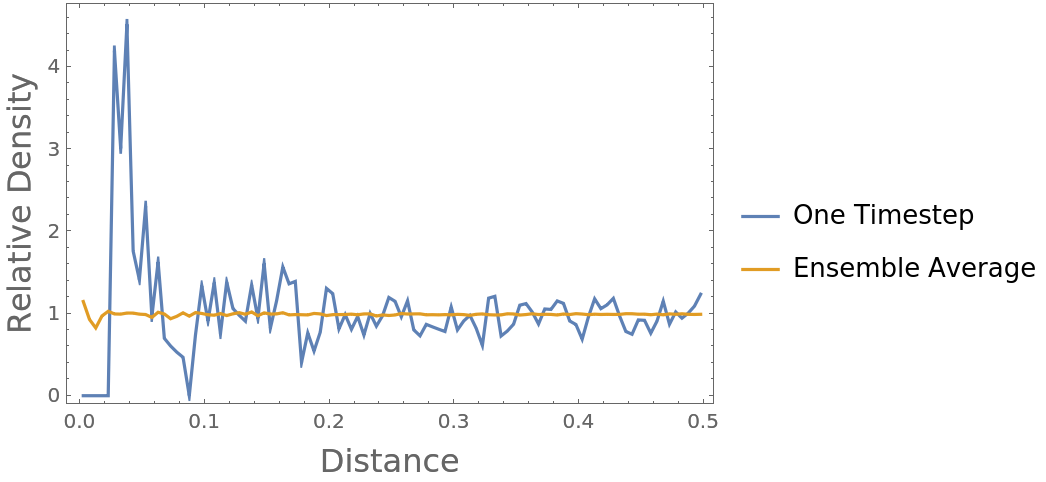
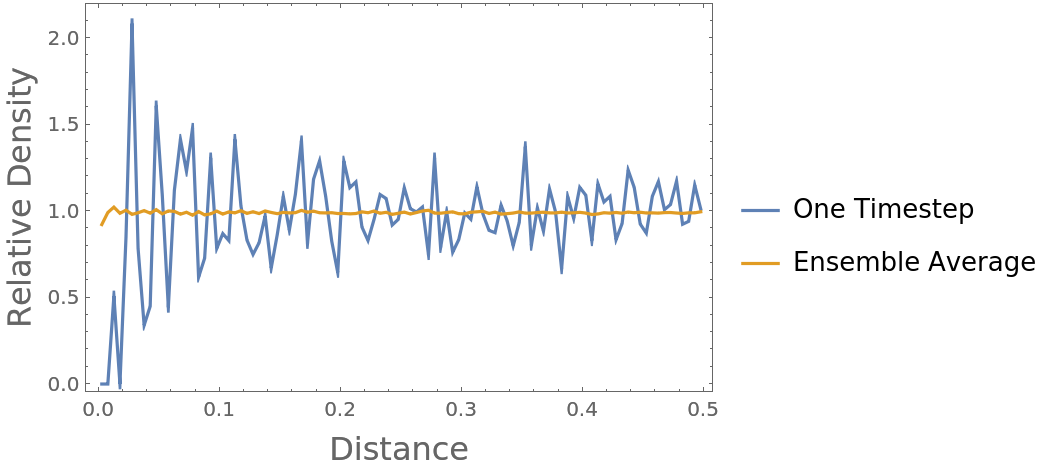
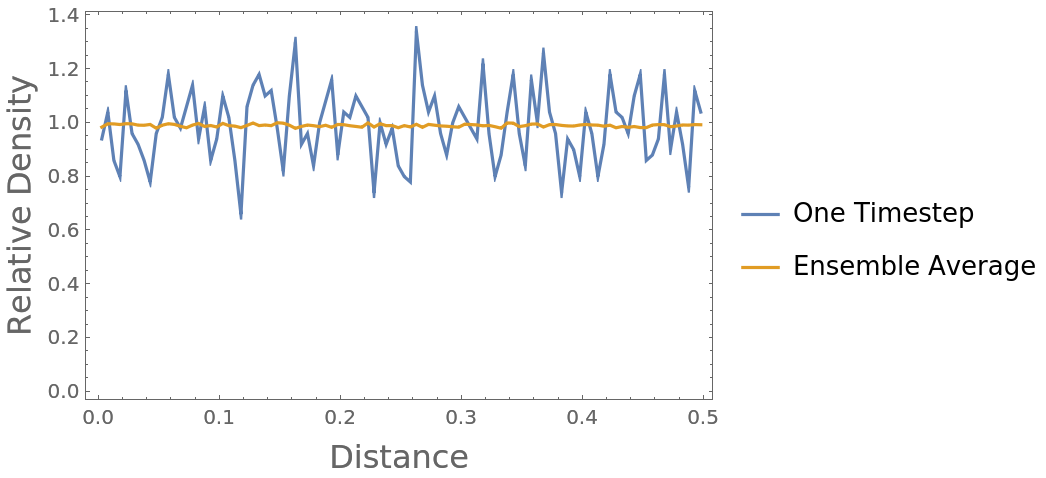
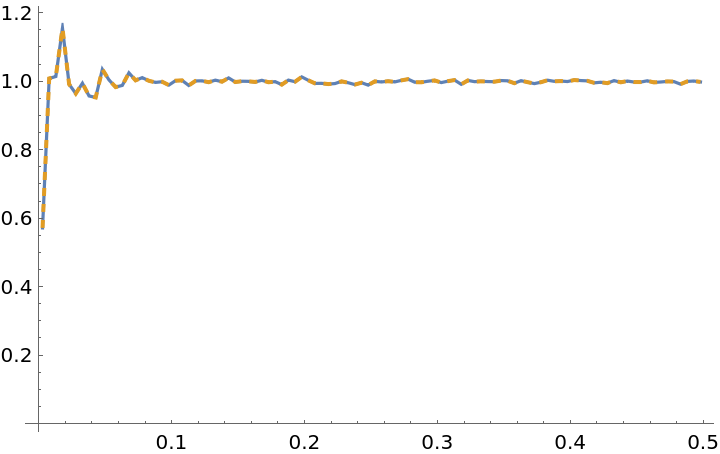
By definition, the RDF of an ideal gas converges to 1 at all distances when provided sufficient data (here, 1000 time steps on 100 positions of 100 particles):
Compute both the radial distribution function of just the first time step, and then that of the ensemble average over all time steps:
As expected, the radial distribution function converges to nearly 1 as sufficient data is introduced:
Normalization by the expected number of particles in that vicinity works in 2D cases as well:
The same is true for 1D cases:
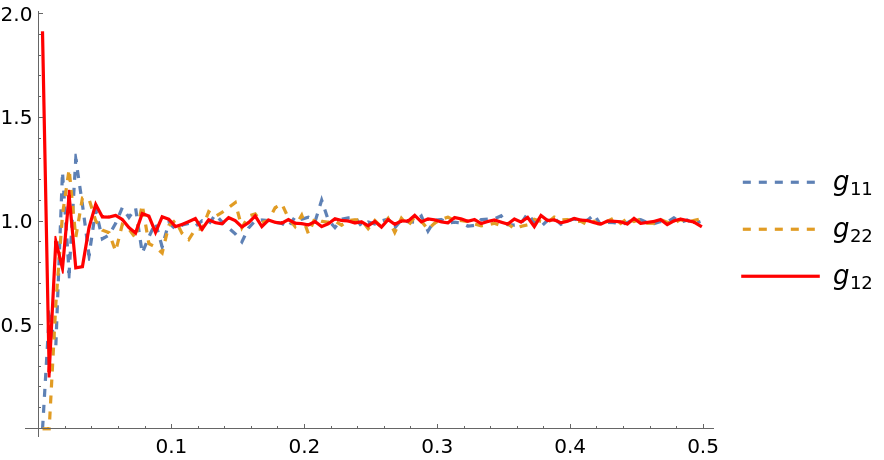
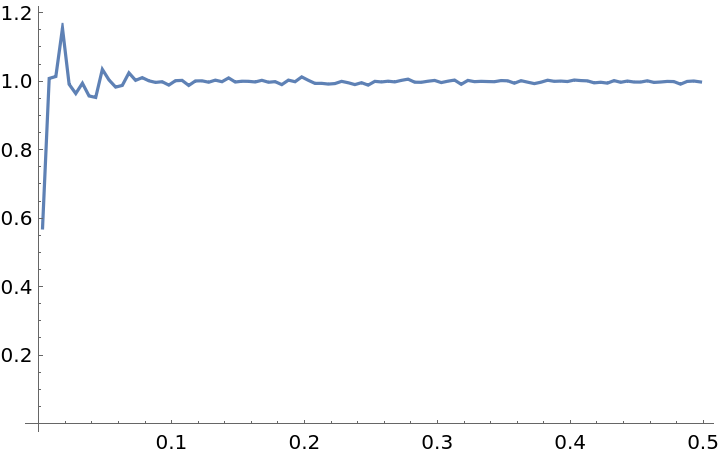
Ensemble average cross-correlations between two distinct populations (lists of coordinates) can also be computed:
Cross-correlations are symmetric, that is, the computation is the same for swapped populations g{XMLElement[i, {}, {XMLElement[span, {class -> stylebox}, {ij}]}]}(r)=g{XMLElement[i, {}, {XMLElement[span, {class -> stylebox}, {ji}]}]}(r):
Possible Issues (4)
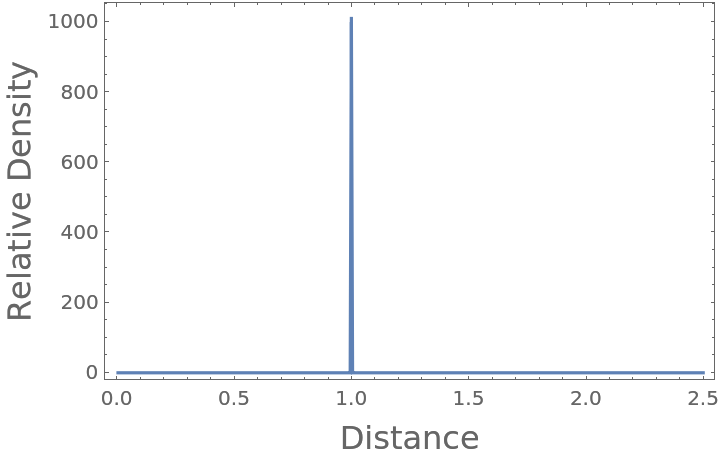
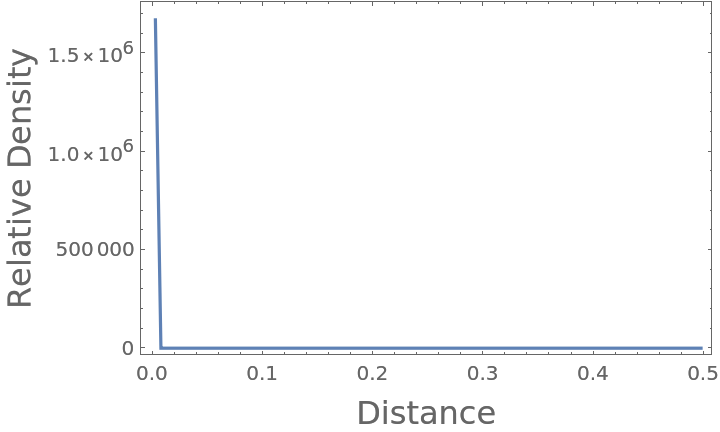
For finite-sized systems, the radial distribution function is accurate out to 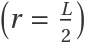 and is thus truncated at this point, beyond which it would artificially decay:
and is thus truncated at this point, beyond which it would artificially decay:
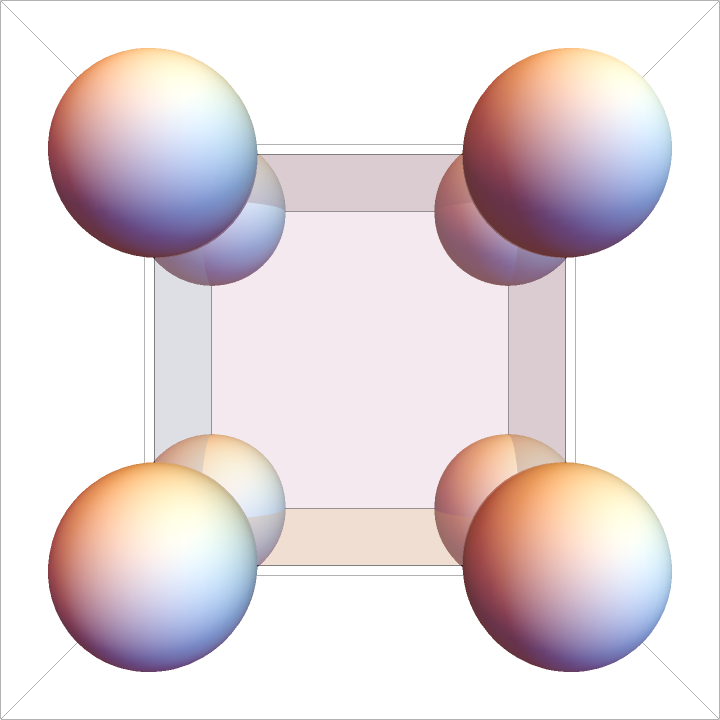
If the box is sufficiently larger than the domain of the particle coordinates, the calculation is as expected (using real particle positions, rather than the minimum image convention under periodicity):
The peaks are at the expected unit distance for the touching particles, at the polygonal face hypotenuse distance, and the interior hypotenuse:
If the box size (L) is too small, the minimum image convention is employed, applying periodicity in each dimension:
In this case, particles are perfectly overlapping and the separation distance between all pairs is r{XMLElement[i, {}, {XMLElement[span, {class -> stylebox}, {ij}]}]}=0, however the convention is to put them in the first non-zero bin:
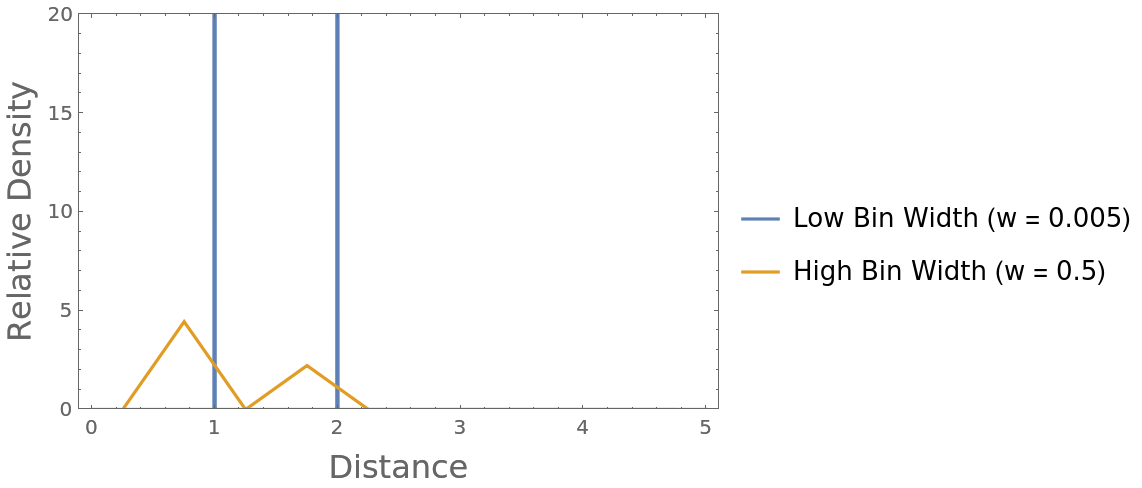
Modifying the concentric shell bin width can affect normalization and positional accuracy, similar to the behavior in Riemann sums with too few discretizing rectangles:
Compare the difference when using two different bin widths:
Neat Examples (3)
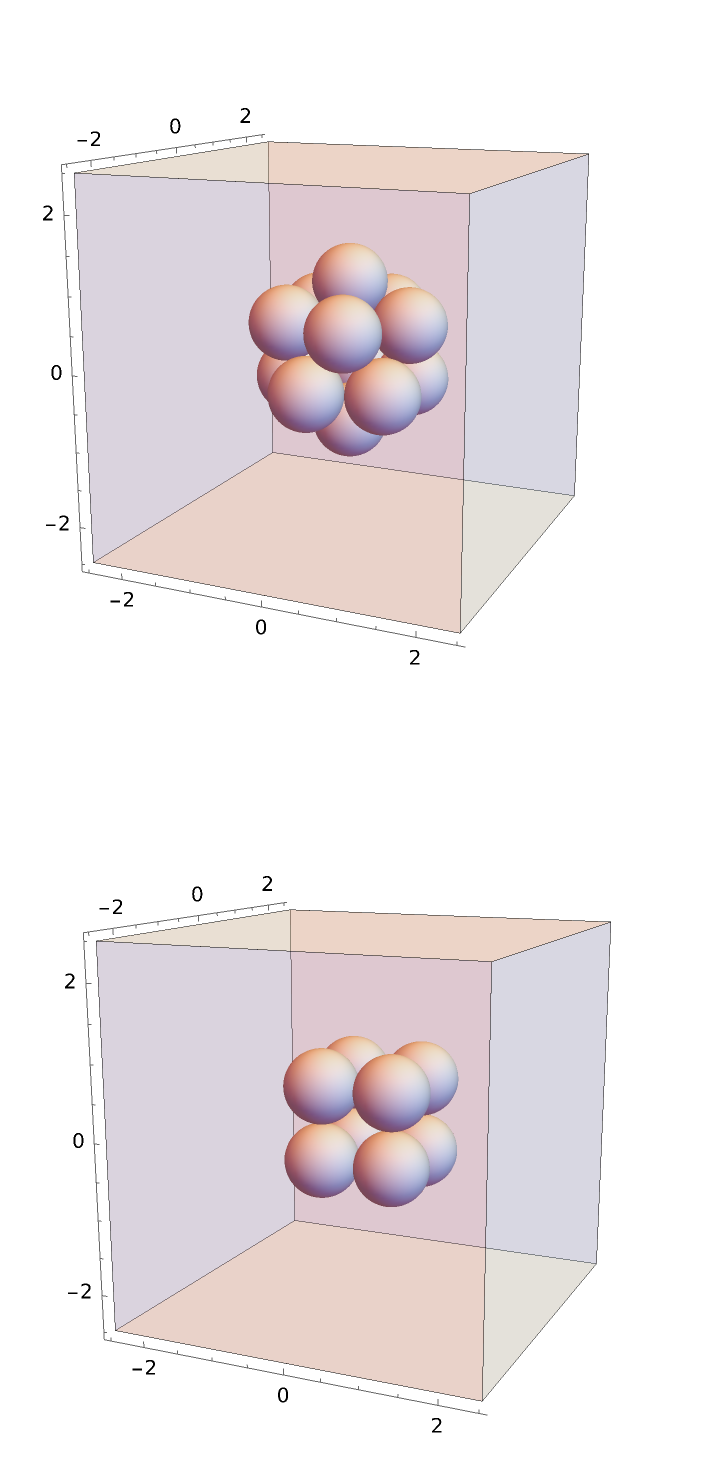
Compute the radial distribution function characteristic of an icosahedral distribution of particles and compare it with that of a cube, each with a minimum separation distance of 1:
Plot the resulting radial distribution functions to compare:
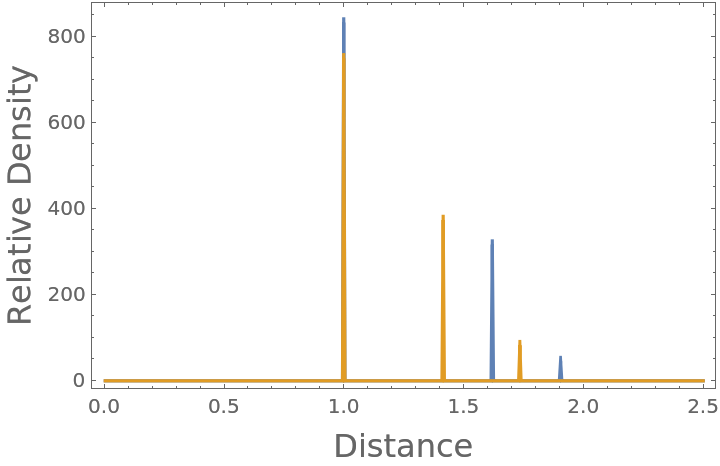
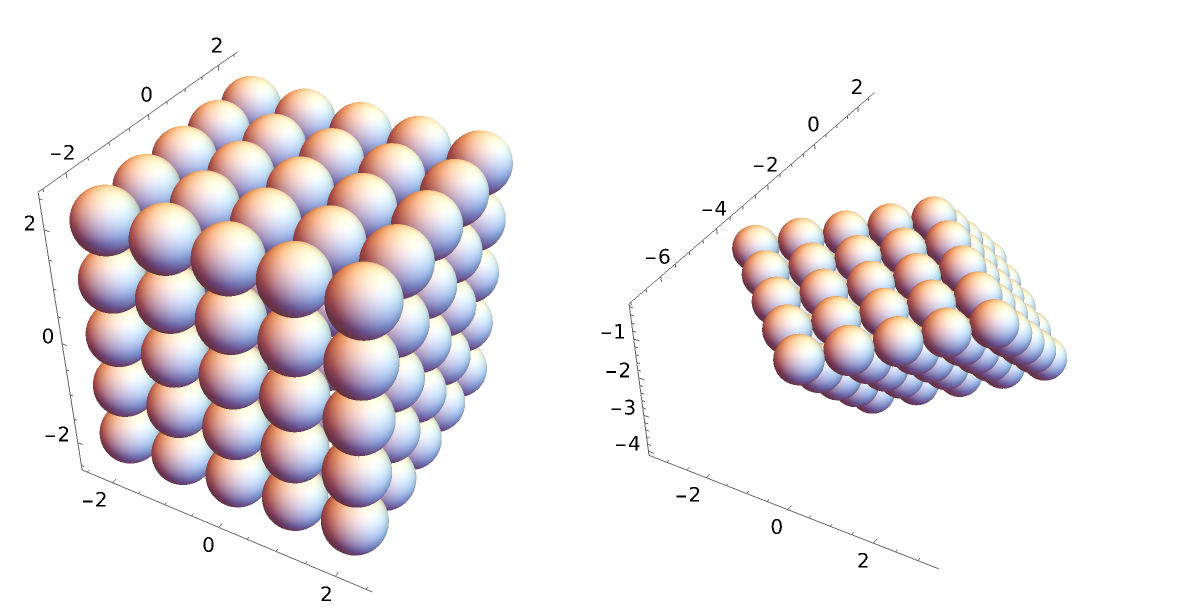
Compare the radial distribution function of both a simple cubic and face-centered cubic (FCC) crystalline lattice (neglecting periodicity, each with nearest neighbors touching at unit lengths):
Compute and plot the radial distribution functions to compare:
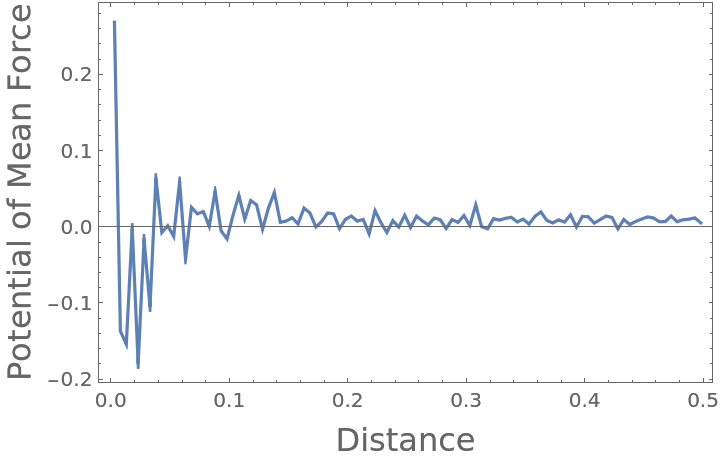
Compute the Potential of Mean Force that has given rise to the interactions, in this example showing that the 3D ideal gas has no potential of interaction:
Compute the corresponding Potential of Mean Force (in units where kBT=1):
It can be seen that despite the noise associated finite data, the Potential of Mean Force is fairly close to zero when averaged over the entire domain:
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9ab5f2b3-4920-4b6a-84bf-dc8612b13d40"]](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/24487dbd74e9973d.png)
![boxLength = 5.0;
coords = N@PolyhedronData["Cube", "Vertices"];
rdfData = ResourceFunction["RadialDistributionFunctionList"][coords, boxLength, 0.005];
Graphics3D[{{Opacity[0.25], Cube[boxLength]}, {Sphere[#, 0.5] & /@ coords}}, Sequence[
Boxed -> False, Axes -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/4982a97d811f3795.png)
![singleTimestepRDF = ResourceFunction["RadialDistributionFunctionList"][
First@bulkCoordsData, 1.0, 0.005];
ensAvgRDF = Mean[Map[
ResourceFunction["RadialDistributionFunctionList"][#, 1.0, 0.005] &, bulkCoordsData]];](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/14be2e201ee0b759.png)
![bulkCoordsData = Table[RandomReal[{0, 1.}, 2], {1000}, {100}];
singleTimestepRDF = ResourceFunction["RadialDistributionFunctionList"][
First@bulkCoordsData, 1.0, 0.005];
ensAvgRDF = Mean[Map[
ResourceFunction["RadialDistributionFunctionList"][#, 1.0, 0.005] &, bulkCoordsData]];](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/62a150fe73cae5a2.png)
![bulkCoordsData = Table[{RandomReal[{0, 1.0}]}, {1000}, {100}];
singleTimestepRDF = ResourceFunction["RadialDistributionFunctionList"][
First@bulkCoordsData, 1.0, 0.005];
ensAvgRDF = Mean[Map[
ResourceFunction["RadialDistributionFunctionList"][#, 1.0, 0.005] &, bulkCoordsData]];](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/2b03cf1f7fdcdd1f.png)
![bulkCoordsData1 = Table[RandomReal[{0, 1.0}, 3], {1000}, {100}];
bulkCoordsData2 = Table[RandomReal[{0, 1.0}, 3], {1000}, {100}];
rdfData12 = Mean@Table[
ResourceFunction["RadialDistributionFunctionList"][
bulkCoordsData1[[i]], 1.0, .005, "ReferenceCoordinates" -> bulkCoordsData2[[i]]], {i, Length@bulkCoordsData1}];
ListLinePlot[rdfData12, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/6945018837aa0a58.png)
![rdfData21 = Mean@Table[
ResourceFunction["RadialDistributionFunctionList"][
bulkCoordsData2[[i]], 1.0, .005, "ReferenceCoordinates" -> bulkCoordsData1[[i]]], {i, Length@bulkCoordsData1}];
ListLinePlot[{rdfData12, rdfData21}, PlotRange -> All, PlotStyle -> {Automatic, {Dashed, Thick}}]](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/03d3cf0d2fd9dc4b.png)
![]() and is thus truncated at this point, beyond which it would artificially decay:
and is thus truncated at this point, beyond which it would artificially decay:![boxLength = 5;
coords = {{0, 0, 0}, {1, 0, 0}};
rdfData = ResourceFunction["RadialDistributionFunctionList"][coords, boxLength];
ListLinePlot[rdfData, Sequence[
PlotRange -> All, Frame -> True, FrameLabel -> Map[Style[#, 16]& , {"Distance", "Relative Density"}]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/131d826dfd200d29.png)
![boxLength = 5;
coords = N@PolyhedronData["Cube", "Vertices"];
rdfData = ResourceFunction["RadialDistributionFunctionList"][coords, boxLength, 0.005];
Graphics3D[{{Opacity[0.25], Cube[boxLength]}, {Sphere[#, 0.5] & /@ coords}}, Sequence[
Boxed -> False, Axes -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/15e8892ebdf2fcb0.png)
![boxLength = 1;
coords = N@PolyhedronData["Cube", "Vertices"];
rdfData = ResourceFunction["RadialDistributionFunctionList"][coords, boxLength, 0.005];
Graphics3D[{{Opacity[0.25], Cube[boxLength]}, {Sphere[#, 0.25] & /@ coords}}, Sequence[
PlotRange -> All, Frame -> True, FrameLabel -> Map[Style[#, 16]& , {"Distance", "Relative Density"}]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/7ca24b3e6f635dc4.png)

![rdfDataLowBinWidth = ResourceFunction["RadialDistributionFunctionList"][coords, boxLength, 0.005];
rdfDataHighBinWidth = ResourceFunction["RadialDistributionFunctionList"][coords, boxLength, 0.5];
ListLinePlot[{rdfDataLowBinWidth, rdfDataHighBinWidth}, PlotRange -> {All, {0, 20}}, PlotLegends -> {"Low Bin Width (w = 0.005)", "High Bin Width (w = 0.5)"}, Frame -> True, FrameLabel -> (Style[#1, 16] &) /@ {"Distance", "Relative Density"}]](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/38e158981b0addbc.png)
![boxLength = 5;
icosaCoords = N@PolyhedronData["Icosahedron", "Vertices"];
cubeCoords = N@PolyhedronData["Cube", "Vertices"];
rdfData = ResourceFunction["RadialDistributionFunctionList"][#, boxLength, 0.005] & /@ {icosaCoords, cubeCoords};
Row@(Graphics3D[{{Opacity[0.25], Cube[boxLength]}, {Sphere[#, 0.5] & /@ #}}, Boxed -> False, Axes -> True, ViewPoint -> {1.35, -3, 0.8}, ImageSize -> 350] & /@ {icosaCoords, cubeCoords})](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/6f393c99ff760c24.png)
![cubicCoords = N@Flatten[
Table[{i, j, k}, {i, -2, 2, 1}, {j, -2, 2, 1}, {k, -2, 2, 1}], 2];
\[ScriptCapitalB] = Normal@LatticeData["FaceCenteredCubic", "Basis"];
fccCoords = N@Flatten[
Table[i \[ScriptCapitalB][[1]] + j \[ScriptCapitalB][[2]] + k \[ScriptCapitalB][[3]], {i, 1, 5}, {j, 1, 5}, {k, 1, 5}], 2];
fccCoords = fccCoords/
Min@DeleteCases[Flatten[DistanceMatrix@fccCoords], x_Real /; x == 0.];
Row@(Graphics3D[{{Sphere[#, 0.5] & /@ #}}, Boxed -> False, Axes -> True, ImageSize -> 300] & /@ {cubicCoords, fccCoords})](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/3f7b96998c55e2f7.png)
![rdfData = ResourceFunction["RadialDistributionFunctionList"][#, 20, 0.005] & /@ {cubicCoords, fccCoords};
ListLinePlot[rdfData, Sequence[
PlotRange -> {{0, 5}, Automatic}, Frame -> True, FrameLabel -> Map[Style[#, 16]& , {"Distance", "Relative Density"}]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/09e/09e1f52f-c32c-418b-8470-86aa014d597d/1-1-0/554158d3febaeab6.png)