Basic Examples (2) 

Compute the radial distribution function from two points:

In[1]:=

Out[1]=

Compute the radial distribution function of a set of coordinates enclosed in a periodic 1D "box" of size (L = 4):

In[2]:=

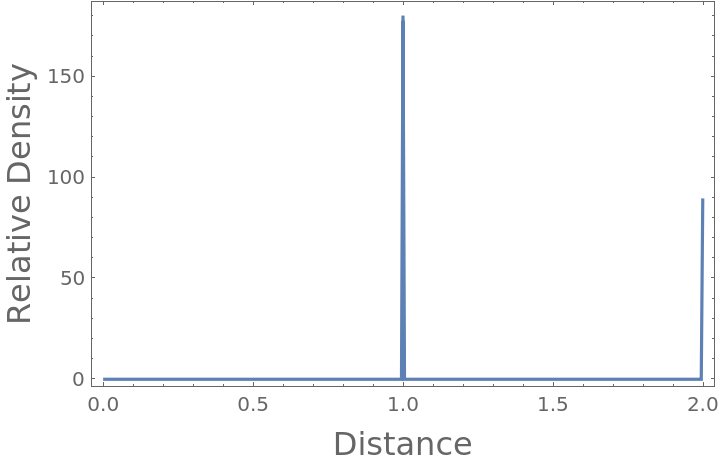
Display the coordinates in number line format along the axis for which the positions differ:

In[3]:=

Out[3]=

The radial distribution function has nonzero peaks at positions near those of the exact distances apart:

In[4]:=

Out[4]=

Plot the radial distribution function characteristic of this system:

In[5]:=

Out[5]=

Options (1) 

RadialDistributionFunctionList takes the same options as Compile, and benefits from automated compilation to C:

In[6]:=

Out[6]=

In[7]:=

Out[7]=

Applications (2) 

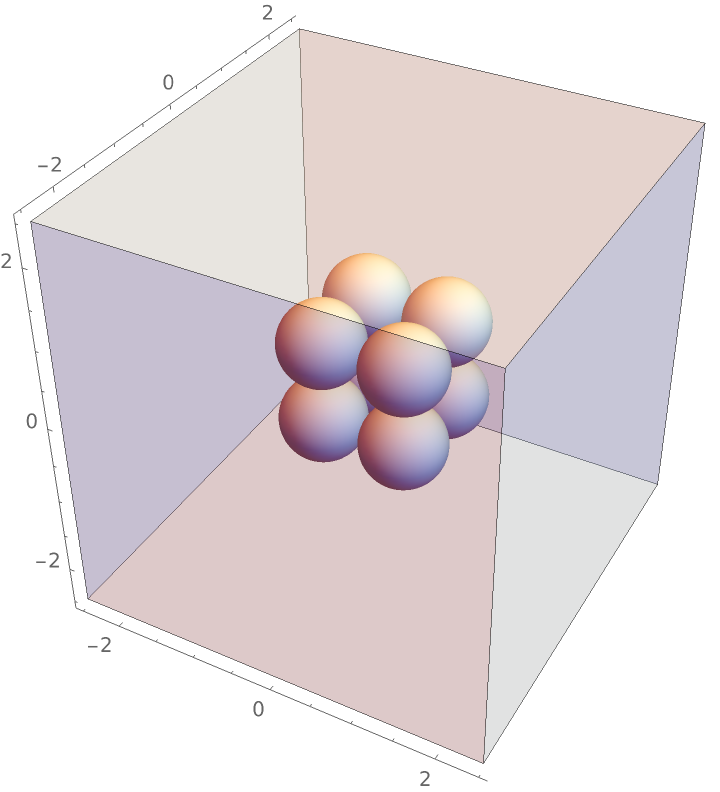
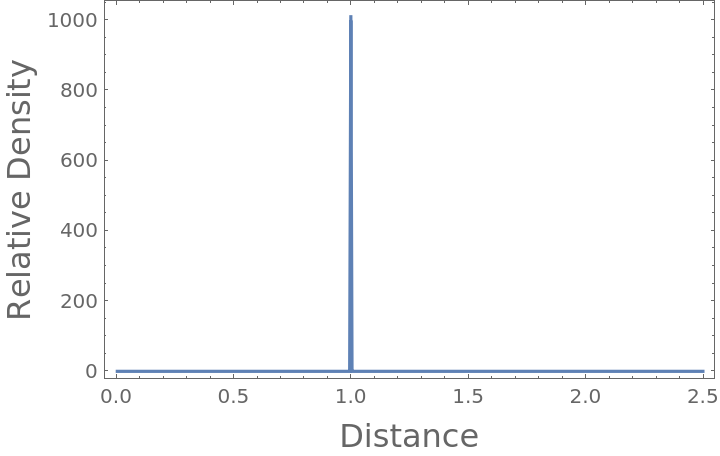
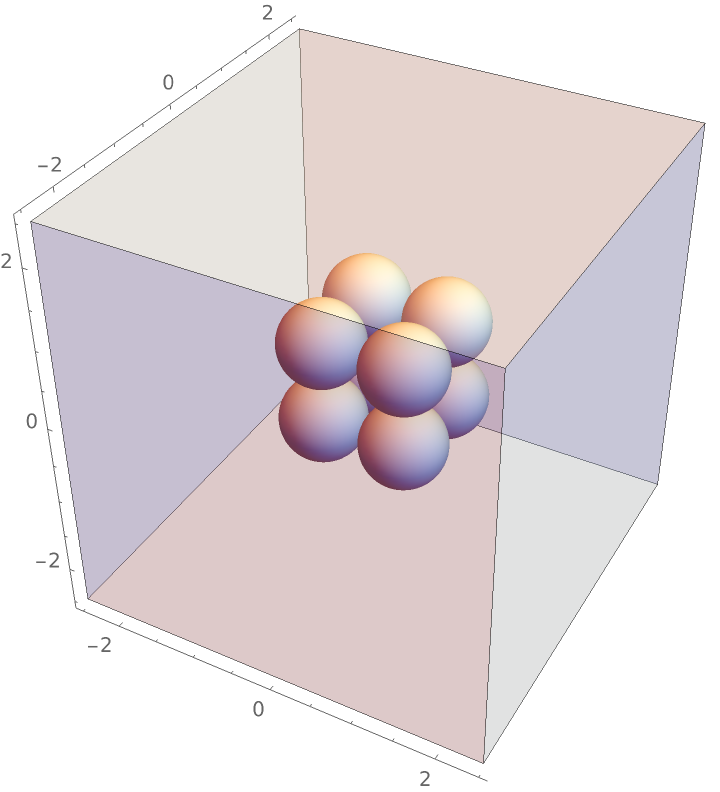
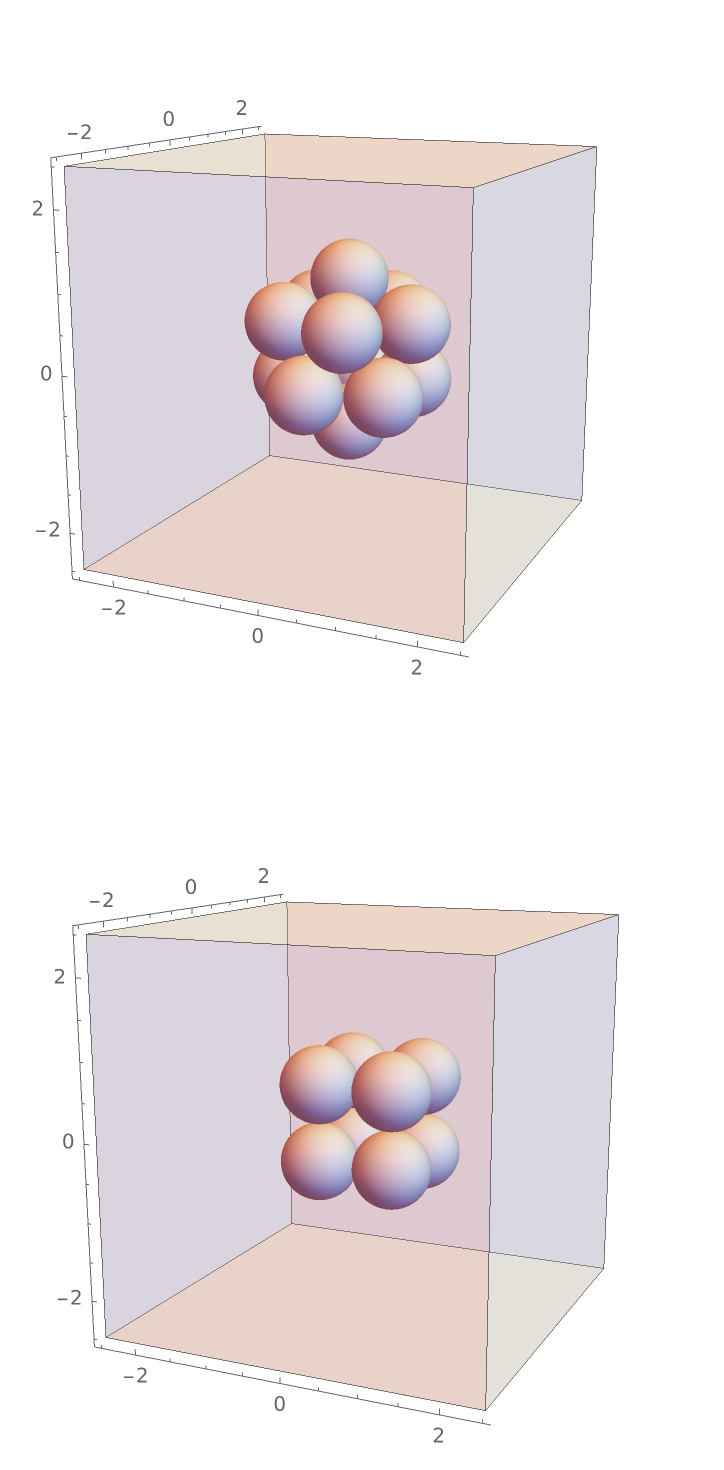
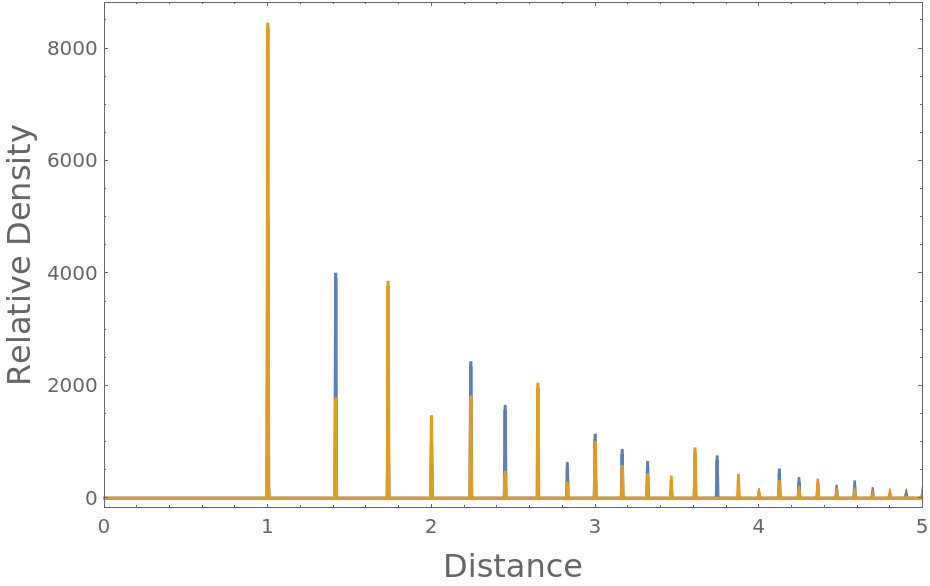
Compute the radial distribution function characteristic of a cube with unit length, enclosed in a sufficiently larger periodic box:

In[8]:=

Out[9]=

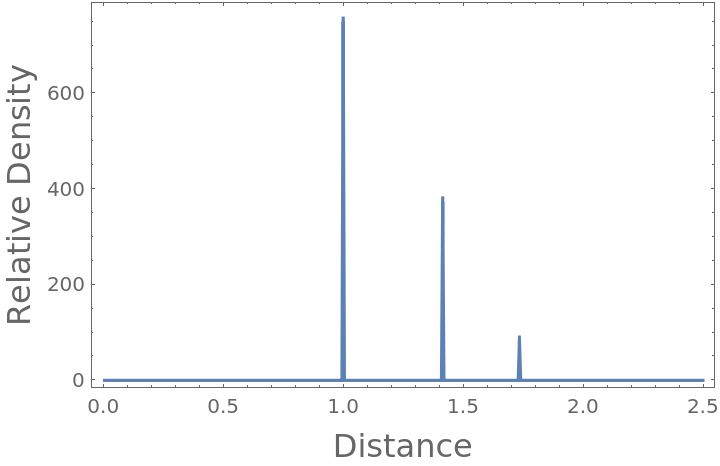
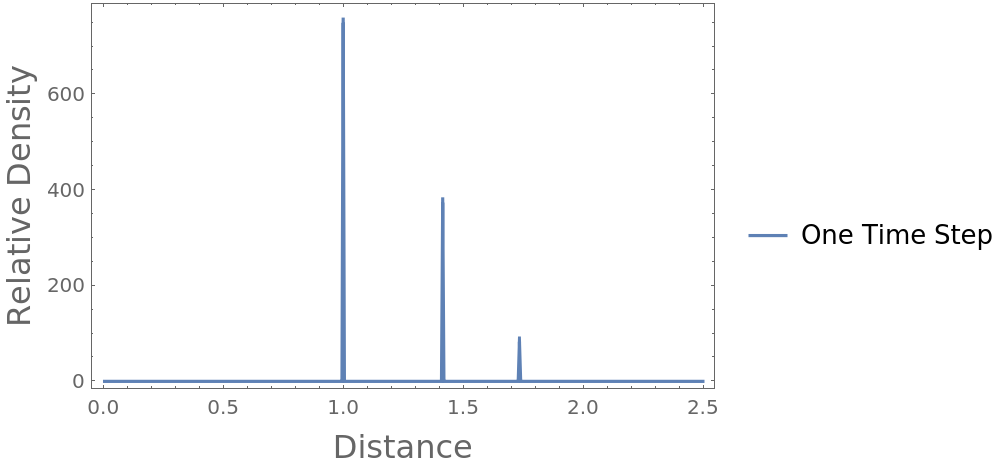
Plot the resulting radial distribution function, where you can see nearest neighbor, polygonal face hypotenuse and internal hypotenuse distances:

In[10]:=

Out[10]=

Properties and Relations (3) 

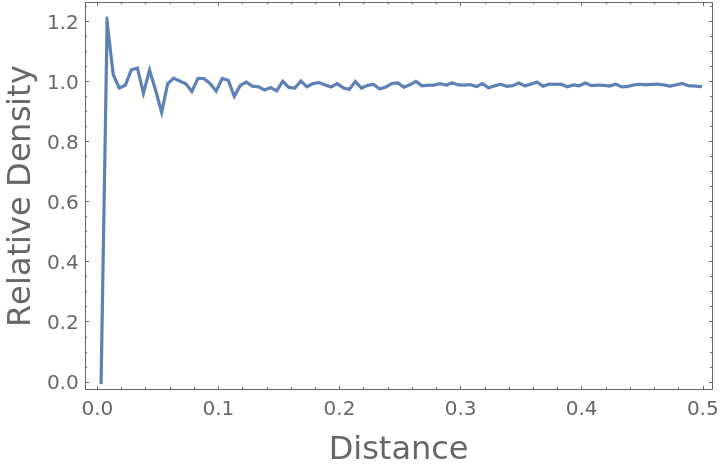
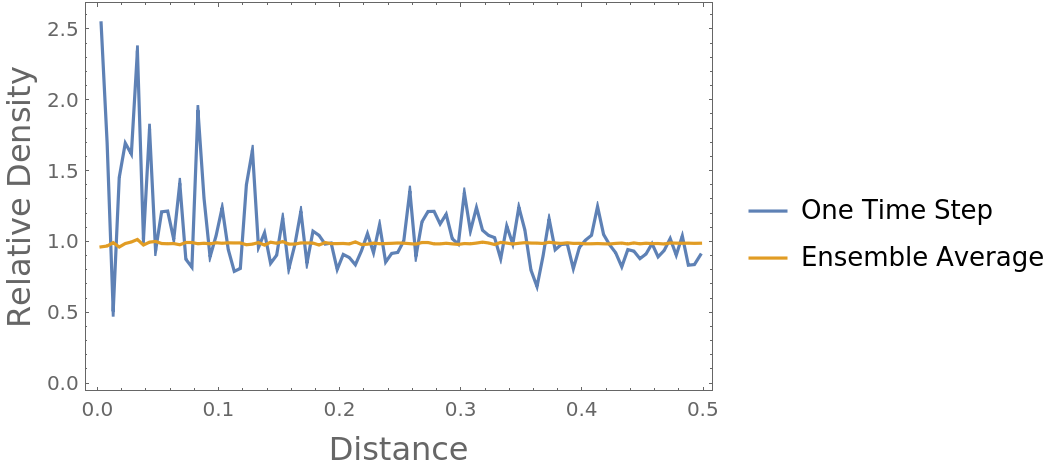
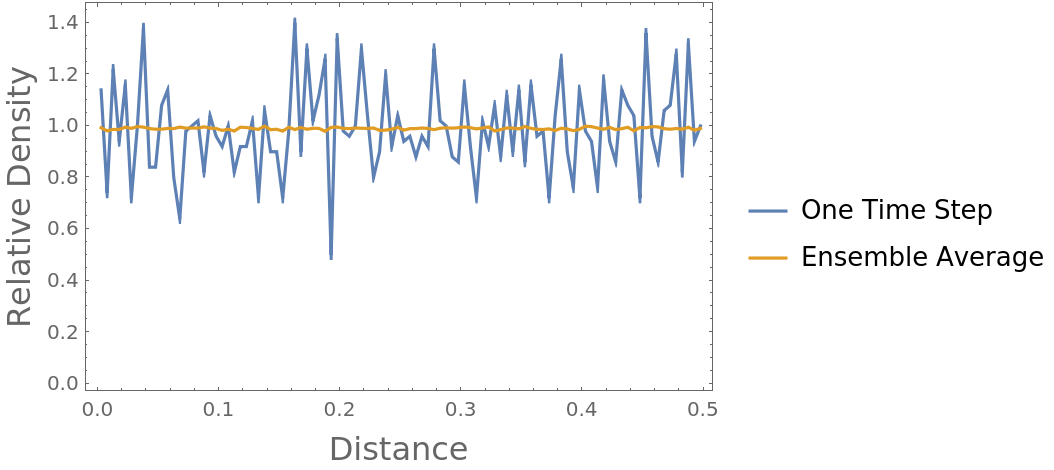
By definition, the radial distribution function of an ideal gas converges to 1 at all distances when provided sufficient data (here, 1000 time steps on 100 positions of 100 particles):

In[11]:=

Compute both the radial distribution function of just the first time step, and then that of the ensemble average over all time steps:

In[12]:=

As expected, the radial distribution function converges to nearly 1 as sufficient data is introduced:

In[13]:=

Out[13]=

Normalization by the expected number of particles in that vicinity works in 2D cases as well:

In[14]:=

In[15]:=

Out[15]=

The same is true for 1D cases:

In[16]:=

In[17]:=

Out[17]=

Possible Issues (4) 

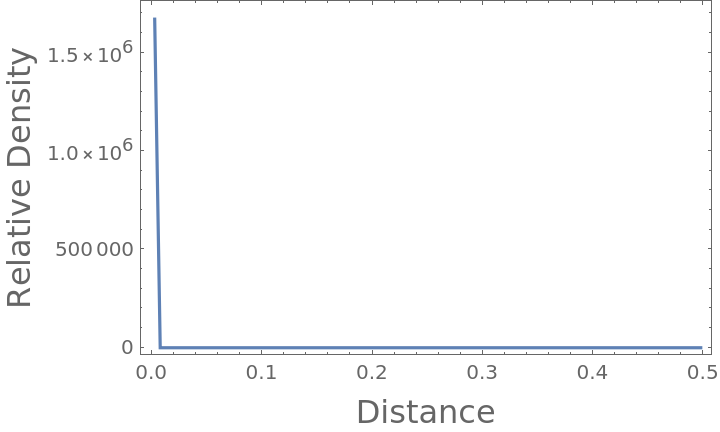
The radial distribution function is accurate out to 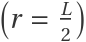and is thus truncated at this point, beyond which it would artificially decay:

In[18]:=

Out[19]=

If the box is sufficiently larger than the domain of the particle coordinates, the calculation is as expected (using real particle positions):

In[20]:=

Out[21]=

The peaks are at the expected unit distance for the touching particles, at the polygonal face hypotenuse distance and the interior hypotenuse:

In[22]:=

Out[22]=

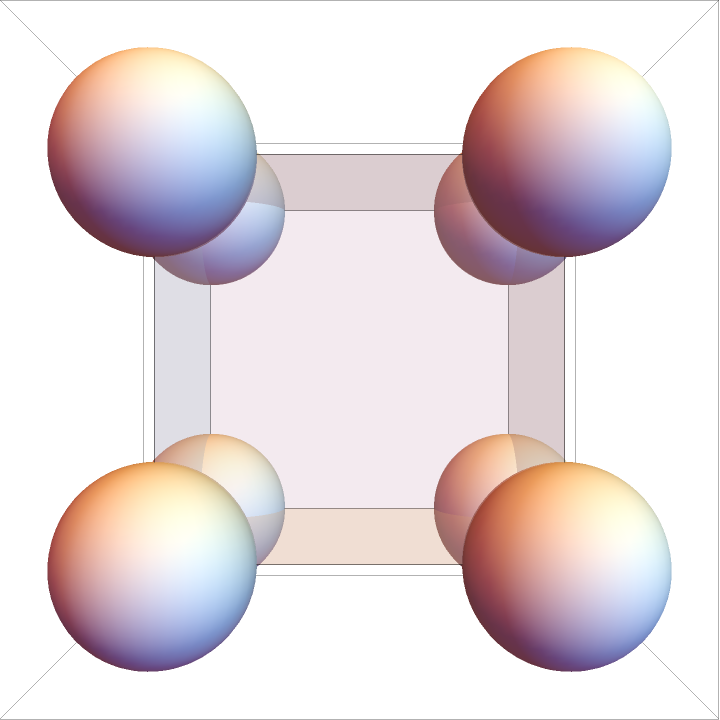
If the box size (L) is too small, the minimum image convention is employed, applying periodicity in each dimension:

In[23]:=

Out[24]=

In this case, particles are perfectly overlapping and the separation distance between all pairs is r_ij=0; however, the convention is to put them in the first nonzero bin:

In[25]:=

Out[25]=

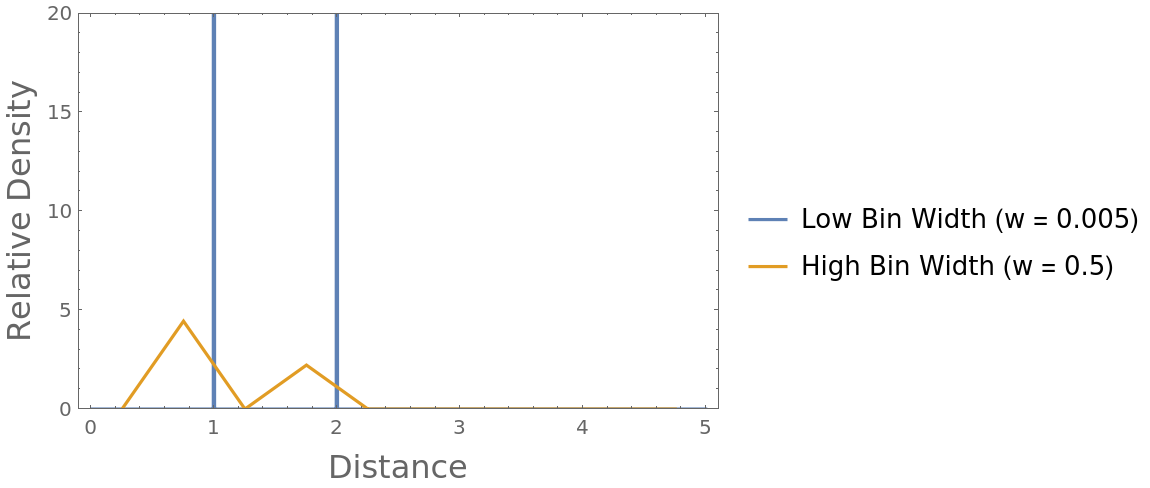
Modifying the concentric shell bin width can affect normalization and positional accuracy, similar to the behavior in Riemann sums with too few discretizing rectangles:

In[26]:=

Out[27]=

Compare the difference when using two different bin widths:

In[28]:=

In[29]:=

Out[29]=

Neat Examples (3) 

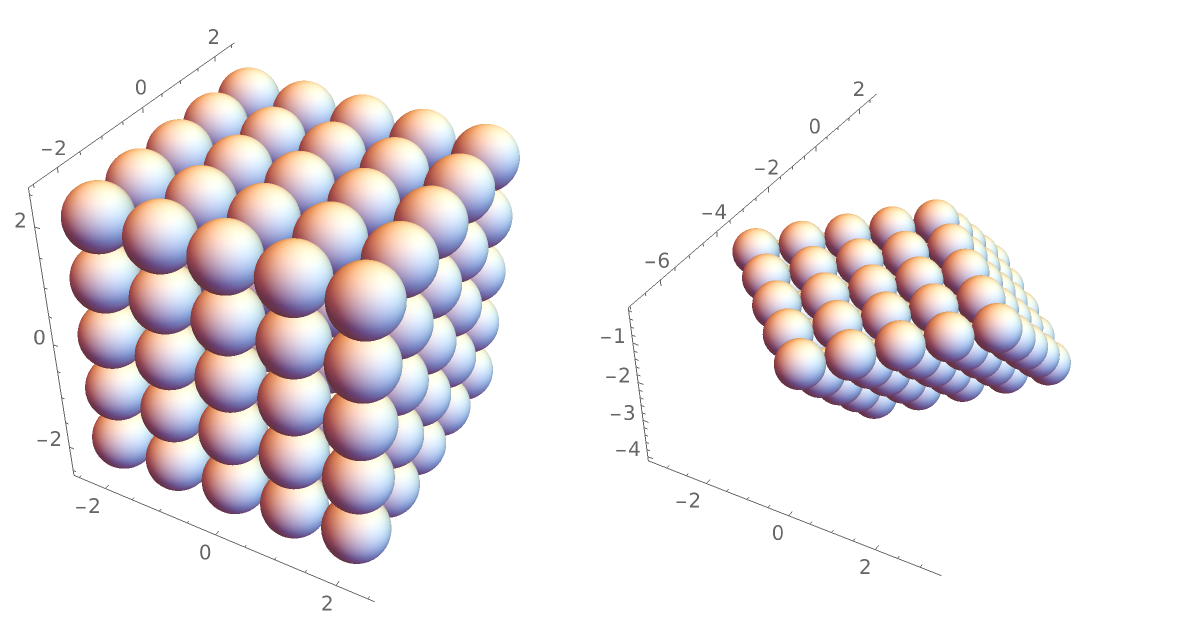
Compute the radial distribution function characteristic of an icosahedral distribution of particles and compare it with that of a cube, each with a minimum separation distance of 1:

In[30]:=

Out[31]=

Plot the resulting radial distribution functions to compare:

In[32]:=

Out[32]=

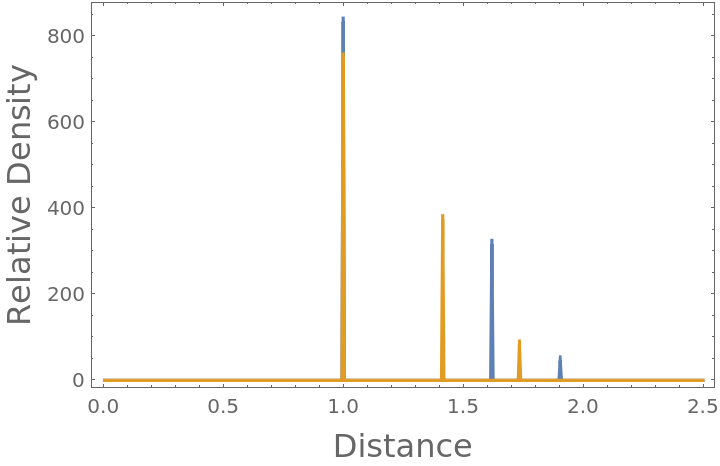
Compare the radial distribution function of both a simple cubic and face-centered cubic (FCC) crystalline lattice (neglecting periodicity, each with nearest neighbors touching at unit lengths):

In[33]:=

Out[37]=

Compute and plot the radial distribution functions to compare:

In[38]:=

Out[39]=

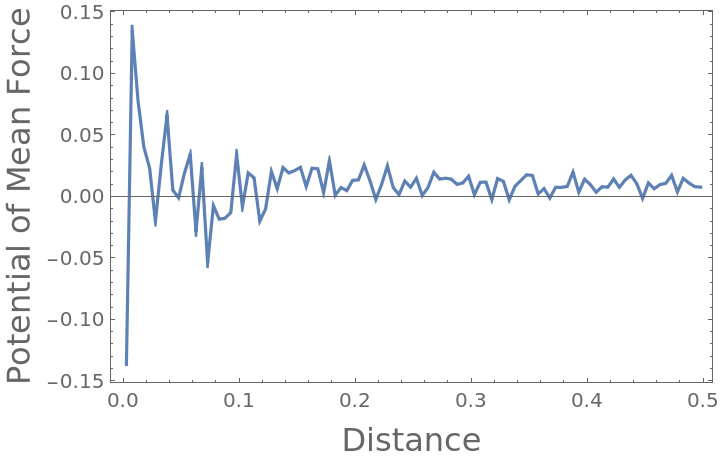
Compute the potential of mean force that has given rise to the interactions, in this example showing that the 3D ideal gas has no potential of interaction:

In[40]:=

In[41]:=

Out[41]=

Compute the corresponding potential of mean force (in units where k_BT=1):

In[42]:=

In[43]:=

Out[43]=

It can be seen that despite the noise associated finite data, the potential of mean force is fairly close to zero when averaged over the entire domain:

In[44]:=

Out[44]=