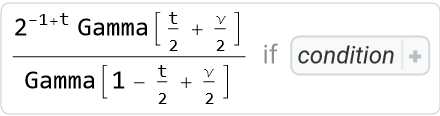Warning: This resource is provisional

Function Repository Resource:

GenericIntegralTransform (2.0.3) current version: 3.1.4 »

Source Notebook

Compute a variety of integral transforms on input expressions

Contributed by: Paco Jain & Oleg Marichev

ResourceFunction["GenericIntegralTransform"][f,z,t,"transform"]

gives the integral transform 𝒯_transform[f(z)](t) of the input function f(z), in terms of new variable t.

Details and Options

ResourceFunction["GenericIntegralTransform"] supports the following options:

GenerateConditions

False

whether to provide conditions under which the given result is valid

"FoxHForm"

False

whether to provide results (where possible) in terms of the FoxH function

The only option values supported for the GenerateConditions options are True and False.

Currently supported values for "transform" include the following:

G-transform

{"G", {{af1_List, ae1_List}, {bf1_List, be1_List}}}



Hankel transform

{"Hankel", {α_, ν_}}



Hilbert transform

{"Hilbert", α_}



Integrate transform

{"Integrate", α_}

put

Laplace transform

{"Laplace", α_}

typeset

Liouville transform

{"Liouville", α_}

definitions

Meijer transform

{"Meijer", {ν_, α_}}

here

Mellin transform

"Mellin"



Neumann transform

{"Neumann", {ν_, α_}}



Riesz transform

{"Riesz", α_}



Stieltjes transform



Struve transform

{"Struve", {ν_, α_}}



Weyl transform

{"Weyl", α_}



Examples

Basic Examples (5)

Compute the Mellin transform of a Bessel function:

In[1]:=

$ResourceFunction["GenericIntegralTransform"][ BesselJ[\[Nu], z], z, t, "Mellin"]$

Out[1]=

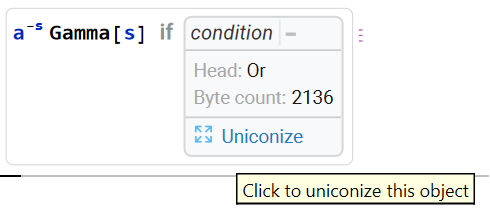
Compute the Mellin transform of an exponential function:

In[2]:=

Out[2]=

Get the conditions of convergence for when the result above is valid:

In[3]:=

Out[3]=

Generically, the result returned is a ConditionalExpression. The conditions under which this result holds can be expanded by clicking the “+“, followed by “Uniconize”, or simply by examining the InputForm:

In[4]:=

Out[4]=

In[5]:=

$ConditionalExpression[ a^-s Gamma[ s], (Abs[Arg[a]] <= \[Pi]/2 && Re[s] < 1 && Re[s] + Inactive[Max][{}] < 1 && Re[s] + Inactive[Min][{0}] > 0) || (Abs[Arg[a]] < \[Pi]/2 && Re[s] + Inactive[Max][{}] < 1 && Re[s] + Inactive[Min][{0}] > 0)] \[AliasDelimiter]$

Compute the Laplace transform of a cosine. By default, GenericIntegralTransform gives results in terms of an Inactive MeijerG function:

In[6]:=

Out[6]=

Use Activate to allow the Inactive[MeijerG] to evaluate to elementary functions:

In[7]:=

Out[7]=

Compute the Hankel transform of an arctangent:

In[8]:=

$ResourceFunction["GenericIntegralTransform"][ ArcTan[z], z, t, {"Hankel", {\[Alpha], \[Nu]}}]$

Out[8]=

To evaluate in terms of simpler functions, use Activate and FunctionExpand:

In[9]:=

Out[9]=

Some results are available in terms of the FoxH function. To return this form where possible, use the "FoxHForm" option:

In[10]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Hankel", {\[Alpha], \[Nu]}}, "FoxHForm" -> True]$

Out[10]=

Scope (24)

G-transform (2)

Compute the G-transform of a sine:

In[11]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"G", {{{}, {\[Alpha]}}, {{0}, {}}}}]$

Out[11]=

Get the result in terms of FoxH:

In[12]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"G", {{{}, {\[Alpha]}}, {{0}, {}}}}, "FoxHForm" -> True]$

Out[12]=

Hankel transform (2)

Compute the Hankel transform of a sine:

In[13]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Hankel", {\[Alpha], \[Nu]}}]$

Out[13]=

Get the result in terms of FoxH:

In[14]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Hankel", {\[Alpha], \[Nu]}}, "FoxHForm" -> True]$

Out[14]=

Hilbert transform (2)

Compute the Hilbert transform of a sine:

In[15]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Hilbert", \[Alpha]}]$

Out[15]=

Get the result in terms of FoxH:

In[16]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Hilbert", \[Alpha]}, "FoxHForm" -> True]$

Out[16]=

Integrate transform (2)

Compute the "Integrate transform" of a sine:

In[17]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Integrate", \[Alpha]}]$

Out[17]=

Get the result in terms of FoxH:

In[18]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Integrate", \[Alpha]}, "FoxHForm" -> True]$

Out[18]=

Laplace transform (2)

Compute the Laplace transform of a sine:

In[19]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Laplace", \[Alpha]}]$

Out[19]=

Get the result in terms of FoxH:

In[20]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Laplace", \[Alpha]}, "FoxHForm" -> True]$

Out[20]=

Liouville transform (2)

Compute the Liousville transform of a sine:

In[21]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Liouville", \[Alpha]}]$

Out[21]=

Get the result in terms of FoxH:

In[22]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Liouville", \[Alpha]}, "FoxHForm" -> True]$

Out[22]=

Meijer transform (2)

Compute the Meijer transform of a sine:

In[23]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Meijer", {\[Alpha], \[Nu]}}]$

Out[23]=

Get the result in terms of FoxH:

In[24]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Meijer", {\[Alpha], \[Nu]}}, "FoxHForm" -> True]$

Out[24]=

Mellin transform (2)

Compute the Mellin transform of a sine:

In[25]:=

Out[25]=

A result in terms of FoxH is not available:

In[26]:=

Out[26]=

Compute the Mellin transform of BesselJ:

In[27]:=

$ResourceFunction["GenericIntegralTransform"][ BesselJ[\[Nu], z], z, t, "Mellin"]$

Out[27]=

Neumann transform (2)

Compute the Neumann transform of a sine:

In[28]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Neumann", {\[Alpha], \[Nu]}}]$

Out[28]=

Get the result in terms of FoxH:

In[29]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Neumann", {\[Alpha], \[Nu]}}, "FoxHForm" -> True]$

Out[29]=

Riesz transform (2)

Compute the Riesz transform of a sine:

In[30]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Riesz", \[Alpha]}]$

Out[30]=

Get the result in terms of FoxH:

In[31]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Riesz", \[Alpha]}, "FoxHForm" -> True]$

Out[31]=

Stieltjes transform (2)

Compute the Stieltjes transform of a sine:

In[32]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Stieltjes", \[Rho]}]$

Out[32]=

Get the result in terms of FoxH:

In[33]:=

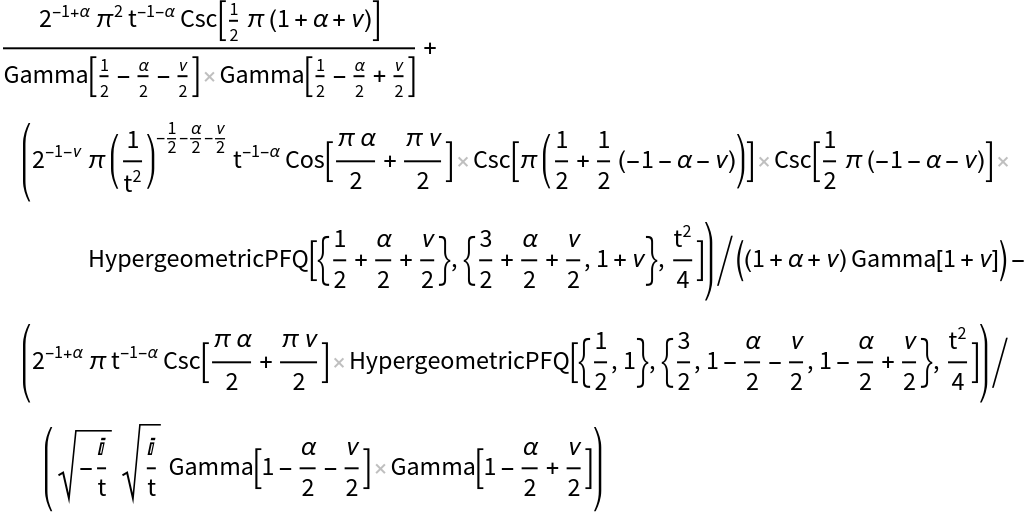
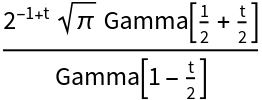
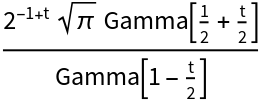
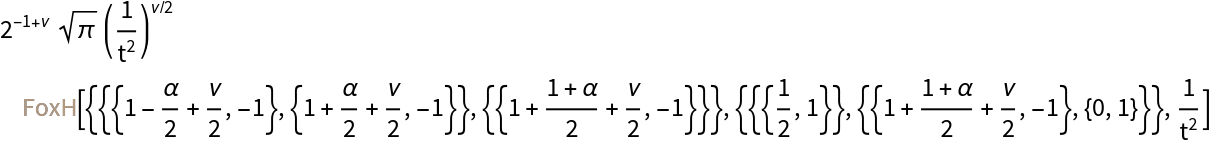
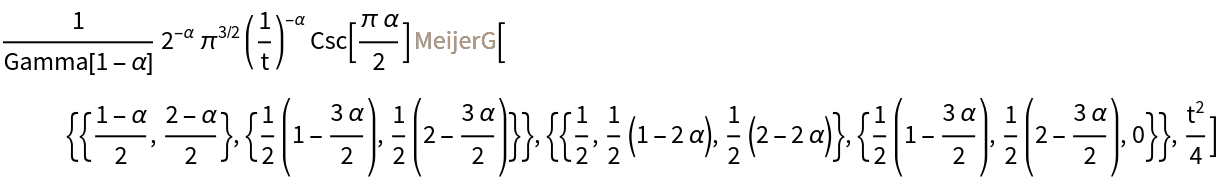
$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Stieltjes", \[Rho]}, GenerateConditions -> False, "FoxHForm" -> True]$

Out[33]=

Struve transform (2)

Compute the Struve transform of a sine:

In[34]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Struve", {\[Nu], \[Alpha]}}]$

Out[34]=

Get the result in terms of FoxH:

In[35]:=

$ResourceFunction["GenericIntegralTransform"][ Sin[z], z, t, {"Struve", {\[Nu], \[Alpha]}}, "FoxHForm" -> True]$

Out[35]=

Options (4)

FoxHForm (2)

Compute a G-transform of a BesselY function:

In[36]:=

$ResourceFunction["GenericIntegralTransform"][ BesselY[\[Nu], z], z, t, {"G", {{{}, {\[Alpha]}}, {{0}, {}}}}]$

Out[36]=

Get the result instead in terms of FoxH:

In[37]:=

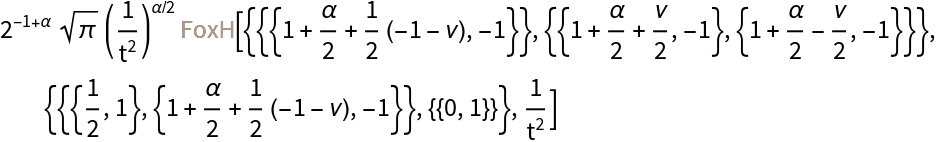
$ResourceFunction["GenericIntegralTransform"][ BesselY[\[Nu], z], z, t, {"G", {{{}, {\[Alpha]}}, {{0}, {}}}}, GenerateConditions -> False, "FoxHForm" -> True]$