Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Warning: This resource is provisional
Function Repository Resource:
Compute a variety of integral transforms on input expressions
ResourceFunction["GenericIntegralTransform"][f,z,t,"type"] gives the integral transform 𝒯type[f](t) corresponding to the input function f(z), in terms of the new variable t. |
| GenerateConditions | True | whether to provide conditions under which the given result is valid |
| "FoxHForm" | False | whether to provide results (where possible) in terms of the FoxH function |
| G-transform | {"G", {{af1_List, ae1_List}, {bf1_List, be1_List}}} | |
| Hankel transform | {"Hankel", {α_, ν_}} | |
| Hilbert transform | {"Hilbert", α_} | |
| Integrate transform | {"Integrate", α_} | |
| Laplace transform | {"Laplace", α_} | |
| Liouville transform | {"Liouville", α_} | |
| Meijer transform | {"Meijer", {ν_, α_}} | |
| Mellin transform | "Mellin" | |
| Neumann transform | {"Neumann", {ν_, α_}} | |
| Riesz transform | {"Riesz", α_} | |
| Stieltjes transform | {{"Stieltjes", ρ_}} | |
| Struve transform | {"Struve", {ν_, α_}} | |
| Weyl transform | {"Weyl", α_} | |
Compute the Mellin transform of a Bessel function:
| In[1]:= |
| Out[1]= |  |
Compute the Mellin transform of an exponential function. Generically, the result returned is a ConditionalExpression:
| In[2]:= |
| Out[2]= |
The conditions under which this result holds can be expanded by clicking the "+", followed by "Uniconize":
| In[3]:= | ![ConditionalExpression[
a^-s Gamma[
s], (Abs[Arg[a]] < \[Pi]/2 && 0 < Re[s] < \[Infinity]) || (Abs[Arg[a]] == \[Pi]/2 && 0 < Re[s] < \[Infinity] && -(1/2) + Re[s] < 1/2)]](https://www.wolframcloud.com/obj/resourcesystem/images/2f5/2f5a9641-7e13-420a-8017-969f8b0cc948/1-2-0/7e26c218bf2f4dc7.png) |
| In[4]:= |
| Out[4]= | 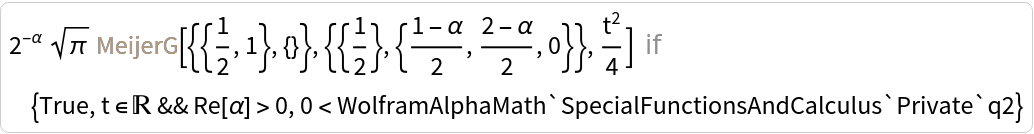 |
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |  |
| In[7]:= |
| Out[7]= | 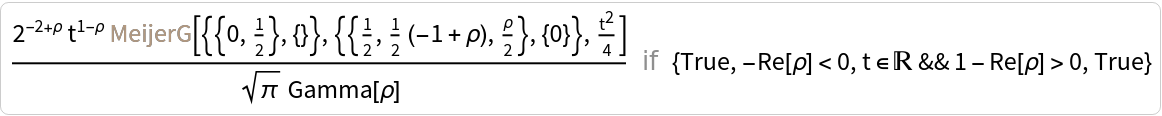 |
| In[8]:= |
| Out[8]= |
Using the option setting GenerateConditions→False to suppress convergence conditions from transform results:
| In[9]:= |
| Out[9]= |
Contrast with the default setting GenerateConditions→True:
| In[10]:= |
| Out[10]= | 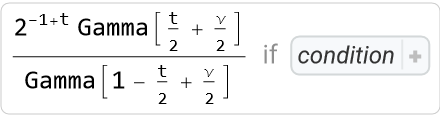 |
This work is licensed under a Creative Commons Attribution 4.0 International License