Hopf bifurcation analysis and first Lyapunov coefficient (3)
Compute the first Lyapunov coefficient for the Brusselator system:
The equilibrium point:
Assume α>0 fixed and take β as a bifurcation parameter to show that the system exhibits a supercritical Hopf bifurcation at X0(α, β=β0), where β0=1+α2.
The Jacobian matrix and its transpose:
Analyse the local stability with the resource function BialternateSum, with β as control parameter:
The critical value of the Hopf bifurcation:
Then, the Brusselator system is locally asymptotically stable at X0(μ) for β<β0 and locally asymptotically unstable for β>β0 (appears a stable limit cycle surrounded the unstable equilibrium point). We verify the previous conclusion by the transversality condition:
The non-trivial equilibrium point at β=β0:
Shift the non-trivial equilibrium point to the origin:
Verify that indeed the non-trivial equilibrium was shifted to the origin:
The Jacobian matrix in the new state variables:
The linear approximation at the origin and its transpose at β=1+α2 and α=ω:
The critical eigenvectors q, 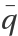 , p,
, p, 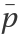 :
:
The normalization 〈pn,q〉=1
The third-order Taylor approximation for the polynomial system
Linear function:
Bilinear function:
Trilinear function:
Verify that the Taylor series expansion of the Brusselator system is correct:
The first Lyapunov coefficient is given by:
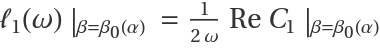
where
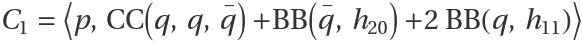
and h20, h11 are given by
h20=(2 ⅈω 𝕀2×2-AA)-1BB(q,q), h11=-AA-1BB(q,q)
First, compute h20, h11 and C1 as follows:
Finally, compute the first Lyapunov coefficient:
The first Lyapunov coefficient is clearly negative for all positive α. Thus, the Hopf bifurcation is nondegenerate and always supercritical.
Compute the first Lyapunov coefficient for the following predator-prey system:
The orbitally equivalent polynomial system:
The Jacobian matrix for the orbitally equivalent polynomial system:
The non-trivial equilibrium point:
The linear approximation at X0(μ):
Analyse the local stability with the resource function BialternateSum, with α as control parameter:
The critical value of the Hopf bifurcation:
Then, the system is locally asymptotically stable for α>α0 and locally asymptotically unstable for α<α0 (with c>d), and can be confirmed by the transversality condition:
The non-trivial equilibrium point at α=α0:
Shift the non-trivial equilibrium point to the origin:
Verify that indeed the non-trivial equilibrium was shifted to the origin:
The Jacobian matrix in the new state variables:
The linear approximation at the origin and at 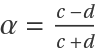 and
and 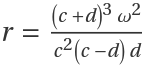 :
:
The critical eigenvectors q, 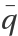 , p,
, p, 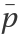 :
:
The normalization 〈pn,q〉=1
The third-order Taylor approximation for the polynomial system
Linear function:
Bilinear function:
Trilinear function:
Verify that the Taylor series expansion of the polynomial system is correct:
The first Lyapunov coefficient is given by:
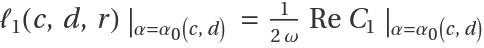
where
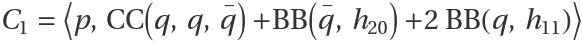
and h20, h11 are given by
h20=(2 ⅈω 𝕀2×2-AA)-1BB(q,q), h11=-AA-1BB(q,q)
First, compute h20, h11 and C1 as follows:
Finally, we compute the first Lyapunov coefficient:
Clearly, the first Lyapunov coefficient is strictly negative for all combinations of the fixed parameters. Therefore, a unique limit cycle emerges from the non-trivial equilibrium via Hopf bifurcation for α<α0.
Compute the first Lyapunov coefficient for the following nonlinear feedback-control system of Lur'e type:
For all values of (α>0,β>0), the Lur'e system has two equilibria, the origin and (1,0,0). At the origin, this system exhibits a supercritical Hopf bifurcation when α=α0, where 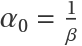 :
:
The Jacobian matrix and its transpose:
Analyse the local stability with the resource function BialternateSum, with β as control parameter:
The critical value of the Hopf bifurcation:
Then, the Lur'e system is locally asymptotically stable at X0(μ) for α>α0 and locally asymptotically unstable for α<α0 (appears a stable limit cycle surrounded the unstable equilibrium point). We verify the previous conclusion by the transversality condition:
The linear approximation at the origin and its transpose at 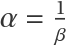 and β=ω2:
and β=ω2:
The critical eigenvectors q, 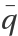 , p,
, p, 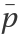 :
:
The normalization 〈pn,q〉=1
The third-order Taylor approximation for the polynomial system
Linear function:
Bilinear function:
Trilinear function:
We verify that the Taylor series expansion of the Lur'e system is correct:
The first Lyapunov coefficient is given by:
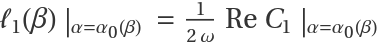
where
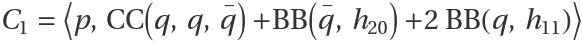
and h20, h11 are given by
h20=(2 ⅈω 𝕀3×3-AA)-1BB(q,q), h11=-AA-1BB(q,q)
First, compute h20, h11 and C1
Finally, compute the first Lyapunov coefficient:
The first Lyapunov coefficient is strictly negative for all positive β. Thus, the Hopf bifurcation is nondegenerate and always supercritical.
Neimark-Sacker bifurcation analysis and first Lyapunov coefficient (19)
The recurrence equation 𝓊k+1=𝓇 𝓊k+1(1-𝓊k-1) is simple population dynamical model, where 𝓊k depict for the density of a population at time k, and 𝓇 is a growth rate. Introducing 𝓊k=𝓊k-1, the above equation can be rewritten as
𝓊k+1=𝓇 𝓊k(1-𝓋k), 𝓋k+1= 𝓋k,
which, in turn, defines the following two-dimensional discrete-time dynamical system
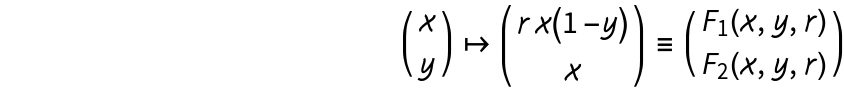
Define the discrete-time dynamical system (1) as follows:
Jacobian matrix:
The non-trivial fixed point:
The linear approximation at X0(r):
The eigenvalues of the linear approximation A:
For 𝓇>5/4 the eigenvalues are complex, so the following shift is made in the growth rate 𝓇 to handle this restriction, and then the eigenvalues of A are computed again:
The value 𝓇0 where the fixed point X0(𝓇0) loses its stability, giving rise to a Neimark-Sacker bifurcation, is given by:
Therefore, the fixed point X0(𝓇0) loses its stability at 𝓇=2 as verified below:
The linear approximation A(𝓇) at the critical bifurcation value 𝓇=2 and its transpose:
The critical multipliers are given by:
The transversality condition:

The nondegeneracy condition:
ζn≠1, for n=1,2,3,4.
The critical eigenvectors q, 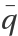 , p,
, p, 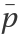 :
:
The normalization 〈pn,q〉=1
The bilinear and trilinear forms to compute the first Lyapunov coefficient:
The first Lyapunov coefficient (additional nondegeneracy condition) is given by
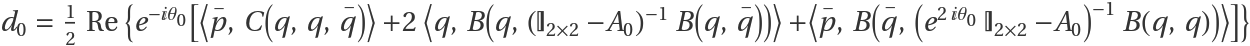
Finally, compute the first Lyapunov coefficient:
Therefore, a unique and stable closed invariant curve bifurcates from the non-trivial fixed point X0(𝓇) for 𝓇>2.
Quadratic coefficients of the normal form for Bogdanov-Takens bifurcation (15)
Compute the quadratic coefficients of the Bogdanov-Takens bifurcation normal form for a predator-prey model with non-linear predator reproduction and prey competition:
The Jacobian matrix:
Look for the Bogdanov-Takens point:
To explicitly handle constraint  , apply the following shift to get the Bogdanov-Takens point:
, apply the following shift to get the Bogdanov-Takens point:
With the above shift in the predator population, the equilibrium point of coexistence and the critical value of bifurcation are as follows:
The linear approximation at x0(ζ0):
Verify that J0(ζ0) has a pair of null eigenvalues:
The critical right eigenvectors q0 and q1:
Verify the conditions 〈J0(ζ0),q0〉=0 y 〈J0(ζ0),q1〉=q0
The transition matrix Q with the critical right eigenvectors:
The critical left eigenvectors p0 and p1:
Verify the conditions 〈J0(ζ0)T,p1〉=0 y 〈J0(ζ0)T,p0〉=p1
Finally, verify the conditions 〈q0,p0〉=〈q1,p1〉=1 y 〈q0,p1〉=〈q1,p0〉=0 and that the matrix J0(ζ0) is similar to a simple Jordan block:
The quadratic coefficients, involved in the nondegeneracy condition, can be computed in the following two ways:
The Bogdanov-Takens bifurcation in this case is non-degenerate when ζ0!=2 and the unique point of degeneracy is:
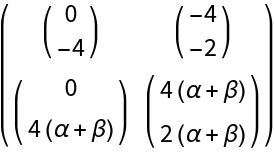
![Lorenz[{x_, y_, z_}][{\[Sigma]_, r_, \[Beta]_}] := {\[Sigma] (y - x), -x z + r x - y, x y - \[Beta] z};
X = {x, y, z};
\[Mu] = {\[Sigma], r, \[Beta]};
Column@Lorenz[X][\[Mu]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/3743327f0c7f3cb3.png)
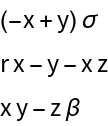
![X0[{\[Sigma]_, r_, \[Beta]_}] := Evaluate[SolveValues[Lorenz[X][\[Mu]] == 0, X]]
X1[{\[Sigma]_, r_, \[Beta]_}] = Part[X0[\[Mu]], 1];
X2[{\[Sigma]_, r_, \[Beta]_}] = Part[X0[\[Mu]], 2];
X3[{\[Sigma]_, r_, \[Beta]_}] = Part[X0[\[Mu]], 3];
Column@Map[Composition[MatrixForm, List], List[X1[\[Mu]], X2[\[Mu]], X3[\[Mu]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/42ce00c8cc44754c.png)
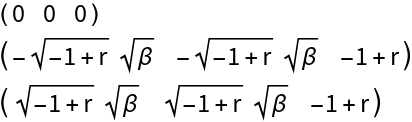
![Column[Map[
MatrixForm@
ResourceFunction["DVectorField"][Lorenz[X][\[Mu]], X, #, 1, "MultilinearFunction"] &, {X1[\[Mu]], X2[\[Mu]], X3[\[Mu]]}], Spacings -> 1]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/311cfddb1c9b4fdc.png)
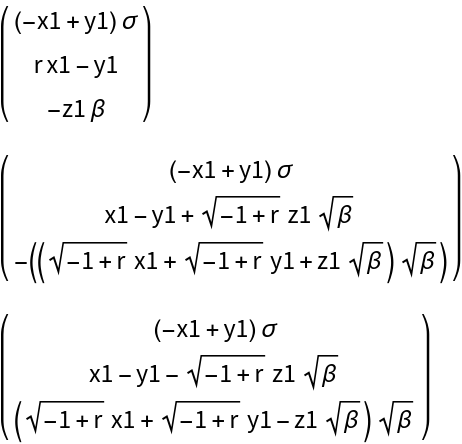
![Column[Map[
MatrixForm@
ResourceFunction["DVectorField"][Lorenz[X][\[Mu]], X, #, 2, "MultilinearFunction"] &, {X1[\[Mu]], X2[\[Mu]], X3[\[Mu]]}], Spacings -> 1]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/6601448c3b235595.png)
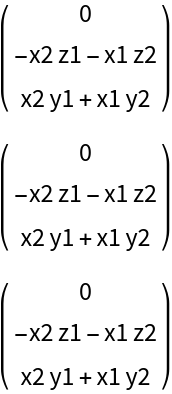
![Brusselator[{x_, y_}][{\[Alpha]_, \[Beta]_}] := {\[Alpha] - (\[Beta] + 1) x + x^2 y, \[Beta] x - x^2 y}
X = {x, y};
\[Mu] = {\[Alpha], \[Beta]};
Column@Brusselator[X][\[Mu]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/7cfbfc0f1ec6795f.png)
![\[Beta]0 = Part[Normal[
SolveValues[
Det[ResourceFunction["BialternateSum"][J[X0[\[Mu]]][\[Mu]]]] == 0 && \[Alpha] > 0 && \[Beta] > 0, \[Beta]]], 1]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/16c597bee8420e83.png)
![Brusselator[{\[Xi]_, \[Eta]_}][\[Alpha]_] := Evaluate@
Collect[ReplaceAll[Thread[{x, y} -> {\[Xi], \[Eta]}]][
Brusselator[
X + X0\[Beta]0][{\[Alpha], \[Beta]0}]], {\[Xi], \[Eta]}, FullSimplify]
X = {\[Xi], \[Eta]};
Column@Brusselator[X][\[Alpha]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/44a324b9882e5ceb.png)
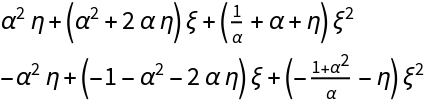
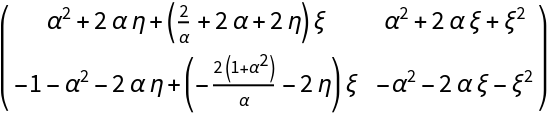
![]() , p,
, p, ![]() :
:![q = Eigenvectors[J0[\[Omega]]][[2]];
qc = ComplexExpand[Conjugate[q]];
pc = Eigenvectors[J0T[\[Omega]]][[1]];
p = ComplexExpand[Conjugate[pc]];
Row[Map[Composition[MatrixForm, List], {q, qc, p, pc}], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/2b916364c1108c31.png)
![pn = 1/cn p;
Row[Map[Composition[MatrixForm, List, Simplify], {pn, J0T[\[Alpha]] . pn - I \[Omega]*pn}], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/71b193681427199d.png)
![AA[{\[Xi]1_, \[Eta]1_}][\[Alpha]_] := Evaluate[
ResourceFunction["DVectorField"][Brusselator[X][\[Alpha]], X, origin, 1, "MultilinearFunction"]]
MatrixForm@AA[{\[Xi]1, \[Eta]1}][\[Omega]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/7d07f2abcac9b774.png)
![BB[{\[Xi]1_, \[Eta]1_}, {\[Xi]2_, \[Eta]2_}][\[Alpha]_] := Evaluate[
ResourceFunction["DVectorField"][Brusselator[X][\[Alpha]], X, origin, 2, "MultilinearFunction"]]
MatrixForm@BB[{\[Xi]1, \[Eta]1}, {\[Xi]2, \[Eta]2}][\[Omega]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/2d755d7d0b133dfe.png)
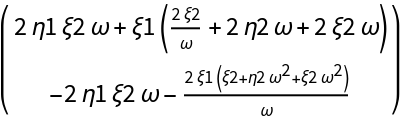
![CC[{\[Xi]1_, \[Eta]1_}, {\[Xi]2_, \[Eta]2_}, {\[Xi]3_, \[Eta]3_}][\[Alpha]_] := Evaluate[
ResourceFunction["DVectorField"][Brusselator[X][\[Alpha]], X, origin, 3, "MultilinearFunction"]]
MatrixForm@
CC[{\[Xi]1, \[Eta]1}, {\[Xi]2, \[Eta]2}, {\[Xi]3, \[Eta]3}][\[Omega]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/71ed7d6ea7bfd7c7.png)
![MatrixForm@{FullSimplify[
Brusselator[X][\[Omega]] - (AA[{\[Xi], \[Eta]}][\[Omega]] + BB[{\[Xi], \[Eta]}, {\[Xi], \[Eta]}][\[Omega]]/2! + CC[{\[Xi], \[Eta]}, {\[Xi], \[Eta]}, {\[Xi], \[Eta]}][\[Omega]]/3!) /. {\[Xi] -> t \[Xi], \[Eta] -> t \[Eta]}]}](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/77d5bd5efa9b4b97.png)
![]()
![]()
![h20 = Simplify[(Inverse[
2 I \[Omega]*IdentityMatrix[2] - J0[\[Omega]]]) . BB[q, q][\[Omega]]];
MatrixForm@List@h20](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/6cb5372d602af34e.png)
![PredatorPrey[{x_, y_}][{c_, d_, r_, \[Alpha]_}] := {r x (1 - x) - (
c x y)/(x + \[Alpha]), -d y + (c x y)/(x + \[Alpha])}
X = {x, y};
\[Mu] = {c, d, r, \[Alpha]};
Column[PredatorPrey[X][\[Mu]]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/529601363fa13f10.png)
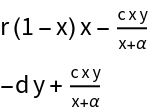
![PolynomialPredatorPrey[{x_, y_}][{c_, d_, r_, \[Alpha]_}] := Evaluate@
Map[Composition[Total, Factor, MonomialList[#, {x, y}] &, Expand, Factor, Times[#, x + \[Alpha]] &], PredatorPrey[X][\[Mu]]]
Column@PolynomialPredatorPrey[X][\[Mu]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/4152b713ea936987.png)
![X0[{c_, d_, r_, \[Alpha]_}] := Evaluate[
Simplify[
Normal[SolveValues[
PolynomialPredatorPrey[X][\[Mu]] == 0 && Reduce[Thread[Flatten[{X, \[Mu]}] > 0]], X][[1]]]]]
MatrixForm@List@X0[\[Mu]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/48d1cfb2eb57ada1.png)
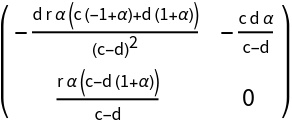
![\[Alpha]0 = Part[Normal[
SolveValues[
Det[ResourceFunction["BialternateSum"][J0[\[Mu]]]] == 0 && 0 < d < c && r > 0 && \[Alpha] > 0, \[Alpha]]], 1]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/68640ada67c159f0.png)
![PolynomialPredatorPrey[{\[Xi]_, \[Eta]_}][{c_, d_, r_}] := Evaluate@
Map[Composition[Total, Collect[#, {\[Xi], \[Eta]}, FullSimplify] &, MonomialList[#, {\[Xi], \[Eta]}] &], ReplaceAll[Thread[{x, y} -> {\[Xi], \[Eta]}]][
PolynomialPredatorPrey[X + X0\[Alpha]0][{c, d, r, \[Alpha]0}]]]
X = {\[Xi], \[Eta]};
\[Mu]3 = {c, d, r};
Column[PolynomialPredatorPrey[X][\[Mu]3]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/73a2b2c16e5ff3f1.png)
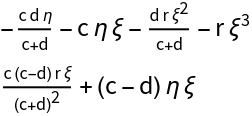
![J[{\[Xi]_, \[Eta]_}][{c_, d_, r_}] := Evaluate[
Collect[D[PolynomialPredatorPrey[X][\[Mu]3], {X}], {\[Xi], \[Eta]}, FullSimplify]]
MatrixForm@J[X][\[Mu]3]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/335bfa79b987d6e3.png)
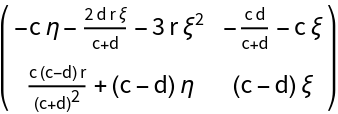
![]() and
and ![]() :
:![r0 = ((c + d)^3 \[Omega]^2)/(c^2 (c - d) d);](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/45480b664a3cd179.png)
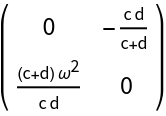
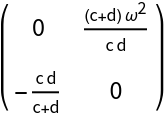
![]() , p,
, p, ![]() :
:![q = -I \[Omega] (c + d)*Eigenvectors[J0[\[Mu]2]][[2]];
qc = ComplexExpand[Conjugate[q]];
pc = -I c d*Eigenvectors[J0T[\[Mu]2]][[1]];
p = ComplexExpand[Conjugate[pc]];
Row[Map[Composition[MatrixForm, List], {q, qc, p, pc}], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/49c8258d62cb2dee.png)
![pn = 1/cn p;
Row[Map[Composition[MatrixForm, List, Simplify], {pn, J0T[\[Mu]2] . pn - I \[Omega]*pn}], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/2beaa2069a4681c4.png)
![Row[Map[Composition[MatrixForm, List, Simplify], {J0[\[Mu]2] . q - I \[Omega]*q, J0[\[Mu]2] . qc + I \[Omega]*qc, J0T[\[Mu]2] . pn - I \[Omega]*pn, J0T[\[Mu]2] . pc + I \[Omega]*pc}], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/0201f1cec99b03df.png)
![AA[{\[Xi]1_, \[Eta]1_}][{c_, d_, r_}] := Evaluate[
ResourceFunction["DVectorField"][PolynomialPredatorPrey[X][\[Mu]3], X, origin, 1, "MultilinearFunction"]]
MatrixForm@AA[{\[Xi]1, \[Eta]1}][\[Mu]3]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/733a7944ea9a4241.png)
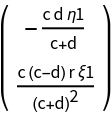
![BB[{\[Xi]1_, \[Eta]1_}, {\[Xi]2_, \[Eta]2_}][{c_, d_, r_}] := Evaluate[
ResourceFunction["DVectorField"][PolynomialPredatorPrey[X][\[Mu]3], X, origin, 2, "MultilinearFunction"]]
MatrixForm@BB[{\[Xi]1, \[Eta]1}, {\[Xi]2, \[Eta]2}][\[Mu]3]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/1db31cc6b211e82d.png)
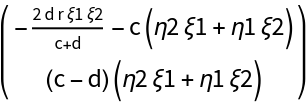
![CC[{\[Xi]1_, \[Eta]1_}, {\[Xi]2_, \[Eta]2_}, {\[Xi]3_, \[Eta]3_}][{c_,
d_, r_}] := Evaluate[
ResourceFunction["DVectorField"][PolynomialPredatorPrey[X][\[Mu]3], X, origin, 3, "MultilinearFunction"]]
MatrixForm@
CC[{\[Xi]1, \[Eta]1}, {\[Xi]2, \[Eta]2}, {\[Xi]3, \[Eta]3}][\[Mu]3]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/20a7153514f2af49.png)
![MatrixForm@{FullSimplify[
PolynomialPredatorPrey[X][{c, d, r0}] - (AA[{\[Xi], \[Eta]}][{c, d, r0}] + BB[{\[Xi], \[Eta]}, {\[Xi], \[Eta]}][{c, d, r0}]/2! + CC[{\[Xi], \[Eta]}, {\[Xi], \[Eta]}, {\[Xi], \[Eta]}][{c, d, r0}]/3!) /. {\[Xi] -> t \[Xi], \[Eta] -> t \[Eta]}]}](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/2cc1a1c7945ff701.png)
![]()
![]()
![h20 = Simplify[(Inverse[
2 I \[Omega]*IdentityMatrix[2] - J0[\[Mu]2]]) . BB[q, q][\[Mu]3]];
MatrixForm@List@h20](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/36c23996b7c0ac98.png)
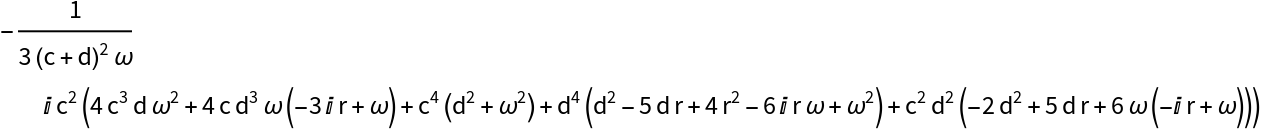
![Lure[{x_, y_, z_}][{\[Alpha]_, \[Beta]_}] := {y, z, -x + x^2 - \[Beta] y - \[Alpha] z};
X = {x, y, z};
\[Mu] = {\[Alpha], \[Beta]};
Column@Lure[X][\[Mu]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/0ed383f49562db3b.png)
![]() :
: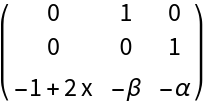
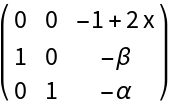
![\[Alpha]0 = Part[Normal[
SolveValues[
Det[ResourceFunction["BialternateSum"][
J[X0[\[Mu]][[1]]][\[Mu]]]] == 0 && \[Alpha] > 0 && \[Beta] > 0, \[Alpha]]], 1]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/713641e9b02bd06b.png)
![]() and β=ω2:
and β=ω2: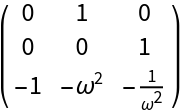
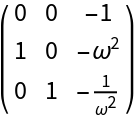
![]() , p,
, p, ![]() :
:![q = -\[Omega]^2*Eigenvectors[J0[\[Omega]]][[3]];
qc = ComplexExpand[Conjugate[q]];
p = -\[Omega]^2*Eigenvectors[J0T[\[Omega]]][[2]] // Expand;
pc = ComplexExpand[Conjugate[p]];
Row[Map[Composition[MatrixForm, List], {q, qc, p, pc}], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/324ec5ec50fc3db4.png)
![pn = Map[Total, MapAt[Composition[FullSimplify, Times[#, I] &], ComplexExpand@ReIm[1/cn pc], {All, 2}]];
Row[Map[Composition[MatrixForm, List, Simplify], {pn, J0T[\[Omega]] . pn - I \[Omega]*pn}], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/33e6d2468948b569.png)
![AA[{x1_, y1_, z1_}][\[Omega]_] := Evaluate[
ResourceFunction["DVectorField"][Lure[X][{\[Alpha]0, \[Beta]}], X, X0[{\[Alpha]0, \[Beta]}][[1]], 1, "MultilinearFunction"]]
MatrixForm@AA[{x1, y1, z1}][\[Omega]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/5aad10d17a816fa9.png)
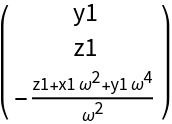
![BB[{x1_, y1_, \[FormalZ]1_}, {x2_, y2_, z2_}][\[Omega]_] := Evaluate[
ResourceFunction["DVectorField"][Lure[X][{\[Alpha]0, \[Beta]}], X, X0[{\[Alpha]0, \[Beta]}][[1]], 2, "MultilinearFunction"]]
MatrixForm@BB[{x1, y1, z1}, {x2, y2, z2}][\[Omega]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/1e59d393150fc775.png)
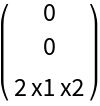
![CC[{x1_, y1_, z1_}, {x2_, y2_, z2_}, {x3_, y3_, z3_}][\[Omega]_] := Evaluate[
ResourceFunction["DVectorField"][Lure[X][{\[Alpha]0, \[Beta]}], X, X0[{\[Alpha]0, \[Beta]}][[1]], 3, "MultilinearFunction"]]
MatrixForm@CC[{x1, y1, z1}, {x2, y2, z2}, {x3, y3, z3}][\[Omega]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/3682259cb7d3ab3c.png)
![MatrixForm@{FullSimplify[
Lure[X][{\[Alpha]0, \[Beta]}] - (AA[X][\[Omega]] + BB[X, X][\[Omega]]/2! + CC[X, X, X][\[Omega]]/3!) /. {x -> t x,
y -> t y, z -> t z}]}](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/41494eb6318362d9.png)
![]()
![]()
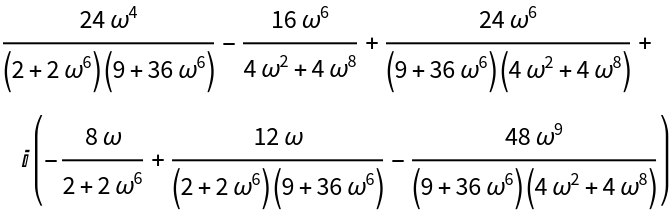
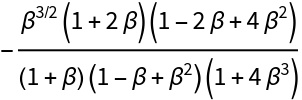
![Simplify@
Numerator[L1]/(Times[#[[1]], #[[2]]] &@
MapAt[Composition[Simplify, Times[#[[1]], #[[2]]] &], List[Extract[FactorList[Denominator[L1]][[All, 1]], {{2}, {3}}], Extract[FactorList[Denominator[L1]][[All, 1]], {4}]], {1}])](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/5124c5b6985630b5.png)
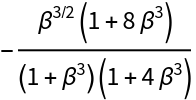
![LogisticMap[{x_, y_}][r_] := {r x (1 - y), x}
X = {x, y};
Column@LogisticMap[X][r]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/533af7d4a79506a4.png)
![\[Zeta]1 = E^(I \[Theta]0);
\[Zeta]2 = E^(-I \[Theta]0);
\[Theta]0 = ArcTan[Sqrt[3]];](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/541b5ac6c2f380b1.png)
![]()
![]() , p,
, p, ![]() :
:![q = ComplexExpand@Eigenvectors[A0][[1]];
qc = ComplexExpand@Eigenvectors[A0][[2]];
p = ComplexExpand@Eigenvectors[A0T][[1]];
pc = ComplexExpand@Eigenvectors[A0T][[2]];
Row[Map[Composition[MatrixForm, List], {q, qc, p, pc}], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/10c059bb44e68b73.png)
![pn = ComplexExpand[1/cn p];
MatrixForm@List@pn](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/2a08e98a5c5e0acb.png)
![BB[{x1_, y1_}, {x2_, y2_}][r_] := Evaluate[
ResourceFunction["DVectorField"][LogisticMap[X][r], X, X0[r], 2, "MultilinearFunction"]]
MatrixForm@BB[{x1, y1}, {x2, y2}][r]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/0fd58d23ffea510a.png)
![CC[{x1_, y1_}, {x2_, y2_}, {x3_, y3_}][r_] := Evaluate[
ResourceFunction["DVectorField"][LogisticMap[X][r], X, X0[r], 3, "MultilinearFunction"]]
MatrixForm@CC[{x1, y1}, {x2, y2}, {x3, y3}][r]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/77bc3ef47e2a3cf0.png)
![]()
![PredatorPrey[{x_, y_}][{\[Gamma]_, \[Epsilon]_, n_}] := Evaluate@{x (1 - y) - \[Epsilon] x^2, -\[Gamma] y + (y/(n + y)) x y}
X = {x, y};
\[Mu] = {\[Gamma], \[Epsilon], n};
Column[PredatorPrey[X][\[Mu]]]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/2f85aeb617162b85.png)
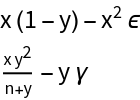
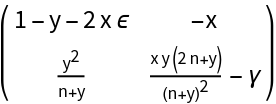
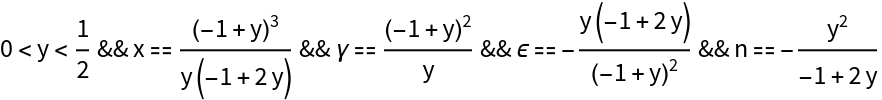
![]() , apply the following shift to get the Bogdanov-Takens point:
, apply the following shift to get the Bogdanov-Takens point:![BTPoint = First@Factor@(SolveValues[
PredatorPrey[X][\[Mu]] == 0 && Tr[J[X][\[Mu]]] == 0 && Det[J[X][\[Mu]]] == 0, {x, \[Gamma], \[Epsilon], n}] /. y -> \[Zeta]0/(2 (1 + \[Zeta]0)))](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/660ab4632c7b9c61.png)
![X0[\[Zeta]0_] := Evaluate[{BTPoint[[1]], \[Zeta]0/(2 (1 + \[Zeta]0))}]
MatrixForm@List@X0[\[Zeta]0]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/2e58cd872e108fac.png)
![J0[\[Zeta]0_] := Simplify@(J[X0[\[Zeta]0]][\[Mu]0[\[Zeta]0]])
MatrixForm@J0[\[Zeta]0]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/3b88e5c6773d7603.png)
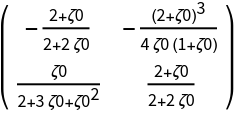


![BB[{x1_, y1_}, {x2_, y2_}][\[Zeta]0_] := Evaluate[
ResourceFunction["DVectorField"][PredatorPrey[X][\[Mu]0[\[Zeta]0]], X, X0[\[Zeta]0], 2, "MultilinearFunction"]]
MatrixForm@BB[{x1, y1}, {x2, y2}][\[Zeta]0]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/3843119435bc6bb3.png)
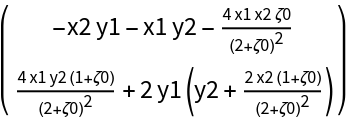
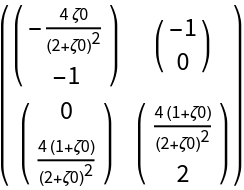
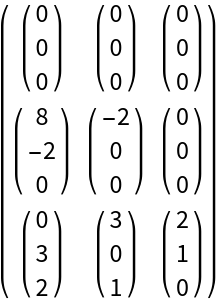
![MatrixForm@
ResourceFunction["DVectorField", ResourceVersion->"1.0.1"][{-x y^2 z + \[Alpha] - \[Beta] x, -y w + x y^2, x y z + w^2, x y z^2 w^3}, {x, y, z, w}, {1, 1, 0, 1}, 3, "MultilinearFunction"]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/1409155f0c82efae.png)
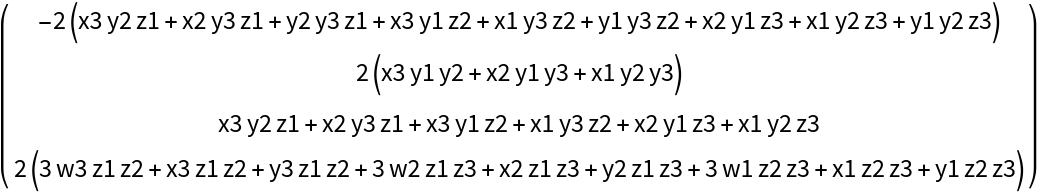
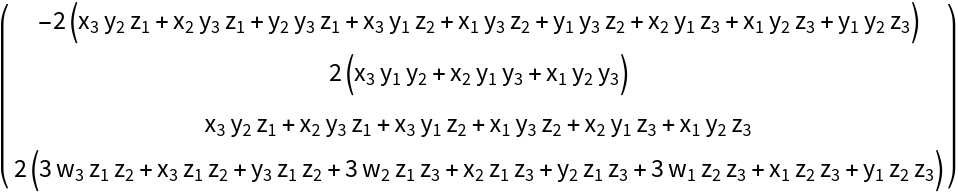
![MatrixForm@
ResourceFunction["DVectorField", ResourceVersion->"1.0.1"][{\[Alpha] - x y^2 + \[Beta] - \[Alpha] x \[Beta], (-y + x y^2) (\[Alpha] + \[Beta])}, {x, y}, {1, 2}, 3, "MultilinearFunction"]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/00ea3f85239b0150.png)
![MatrixForm@
ResourceFunction["DVectorField", ResourceVersion->"1.0.1"][{\[Alpha] - x y^2 + \[Beta] - \[Alpha] x \[Beta], (-y + x y^2) (\[Alpha] + \[Beta])}, {x, y}, {1, 2}, 3, "MultilinearFunction"]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/154c06638500ac82.png)
![D20[{{x1_, y1_}, {x2_, y2_}}] = ResourceFunction["DVectorField"][{x - y^2, 2 y/x}, {x, y}, {1, 2}, 2,
"MultilinearFunction"]](https://www.wolframcloud.com/obj/resourcesystem/images/d71/d71db709-5757-44e8-a522-45a3bdfaf3d6/1-0-1/07f03868c1d96506.png)