Basic Examples (2)
Convert a symbol to a subscripted symbol:
Convert multiple symbols:
Scope (9)
Use with a list of expressions:
Use with a symbolic matrix:
Use with a tensor of rank 3:
Use with a tensor of rank 4:
Use with a nonlinear system of ordinary differential equations:
Use with a system of partial differential equations:
SymbolToSubscript optionally uses "NestedIndices" to represent subscriptable symbols with multiple indices in a nested format:
SymbolToSubscript optionally uses "MultipleIndices" to represent subscriptable symbols with multiple indices, separating them by commas:
Both the base and subscript in the output are symbols and inherit any existing definitions:
Options (1)
FormatStyle (1)
SymbolToSubscript includes an option that enables its outputs to be represented in a string format:
Applications (3)
Format a symbolic polynomial:
Format a symbolic matrix:
Use SymbolToSubscript and TeXForm:
Define a function for making a Vandermonde matrix:
Format a Vandermonde matrix:
The SymbolToSubscript command allows TeXForm to be used correctly when we have expressions with subscripts that are written as symbols:
Possible Issues (2)
The function SymbolToSubscript, when transforming an expression into subscript format, may encounter a potential issue. As the function dissects the expression and processes each component via ToExpression, numerical expressions are simplified by default. For instance, if the only numeric indices we have are zero followed by one, we are left with just the number one. This interpretation leads to the conversion of this pair of numbers into a single subscript, which may not be the intended outcome. To circumvent this problem and provide more granular control over the output, the function is equipped with options that allow for improved handling of how expression components are processed and displayed. Let's illustrate this with an example:
To handle the above problem, SymbolToSubscript has the "ToStringFormat" option:
We can also address this issue using the options for nested indices and multiple indices separated by commas, as demonstrated below:
The SymbolToSubscript function provides a simple way to handle subscriptable symbols. However, it's essential to be mindful of protected symbols such as E (exponential constant), π (Pi), I (Imaginary unit), among others when using this function. Let's illustrate this with an example:
To avoid the above misunderstandings, users are highly advised not to use protected symbols.
![ResourceFunction[
"SymbolToSubscript"][{Sin[t], Cos[x], Tan[s], Cot[x1], BesselJ[0, x1[t] + x2[t]], Csch[(x^(m - 2) - x3) (x^(n + 1) + x2)]}]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/2d385984d8517e2f.png)

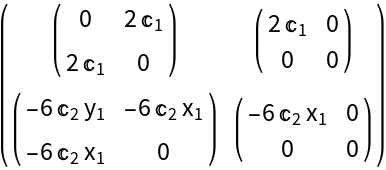
![ResourceFunction["SymbolToSubscript"]@{\!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(u1[t, x]\)\) == \!\(
\*SubscriptBox[\(\[PartialD]\), \(x\)]\((\((u2[t, x] - 1)\)\
\*SubscriptBox[\(\[PartialD]\), \(x\)]u1[t, x])\)\) + (16 x t - 2 t - 16 (u2[t, x] - 1)) (u1[t, x] - 1) + 10 x E^(-4 x), \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(u2[t, x]\)\) == \!\(
\*SubscriptBox[\(\[PartialD]\), \({x, 2}\)]\(u2[t, x]\)\) + \!\(
\*SubscriptBox[\(\[PartialD]\), \(x\)]\(u1[t, x]\)\) + 4 u1[t, x] - 4 + x^2 - 2 t - 10 t E^(-4 x)}](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/6056cc55547d97d3.png)
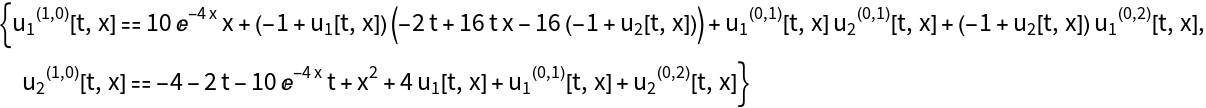
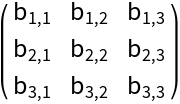
![gridData = {{"No String Format", "String Format"}, TeXForm /@ {ResourceFunction["SymbolToSubscript"][x12], ResourceFunction["SymbolToSubscript"][x12, "FormatStyle" -> "ToStringFormat"]}};
Grid[gridData, Frame -> All, Background -> {None, {LightGray, {White}}}]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/1cfd132d6c39dadd.png)
![polynomial[var_Symbol, coeff_Symbol, n_Integer?NonNegative] := Total[Array[
Times[ToExpression[
ToString[coeff] <> ToString[FromDigits[{n - ##}]]], var^#] &, n + 1, 0]]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/26f00dfd2ed2f582.png)
![Row[Map[MatrixForm, MapAt[Map[ResourceFunction["SymbolToSubscript"], #] &, ConstantArray[Matrix[x, {5, 5}], 2], {2}]], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/1b151ef73580e700.png)
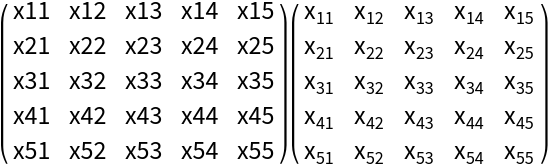
![Row[Map[MatrixForm, MapAt[ResourceFunction["SymbolToSubscript"][#, "MultipleIndices"] &,
ConstantArray[Matrix[x, {5, 5}], 2], {2}]], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/16a3aecde602663a.png)
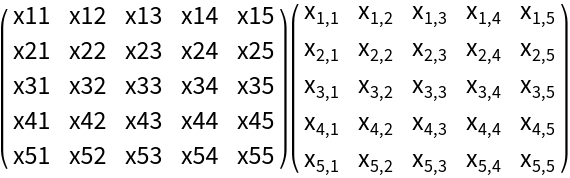

![Row[Map[MatrixForm, MapAt[Map[ResourceFunction["SymbolToSubscript"], #] &, ConstantArray[vandermondeMatrix[x, 5], 2], {2}]], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/3ec33fc9e6d186ec.png)
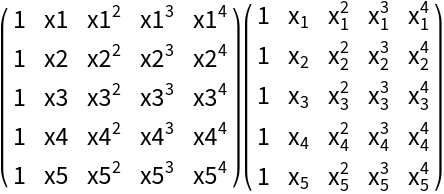
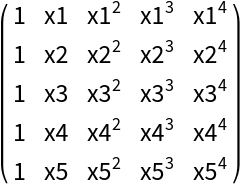

![polynomial[var_Symbol, coeff_Symbol, n_Integer?NonNegative] := Total[Array[
Times[ToExpression[
ToString[coeff] <> ToString[FromDigits[{n - ##}]]], var^#] &, n + 1, 0]]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/30a74dc1d9bfdc84.png)


![ResourceFunction["SymbolToSubscript"]@
ResourceFunction[
"SolutionRulesToFunctions"][\[Theta][t] -> \[Theta]0 + t \[Omega]0 + (g t^2 Sin[\[Alpha]])/(3 R)]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/1c37e381f29386ca.png)
![gridData = {{"Nested Indices Format", "Multiple Indices Format"}, TeXForm /@ {ResourceFunction["SymbolToSubscript"][x1y2, "NestedIndices"], ResourceFunction["SymbolToSubscript"][x1y2, "MultipleIndices"]}};
Grid[gridData, Frame -> All, Background -> {None, {LightGray, {White}}}]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/660841aaa30160da.png)