Basic Examples (2)
Use SymbolToSubscript with an unprotected symbol:
Use SymbolToSubscript with a list of unprotected symbols:
Scope (9)
Use SymbolToSubscript with a list of functions with protected heads:
Use SymbolToSubscript with the default form for the ith constant C[i]:
Use SymbolToSubscript with symbolic matrix:
Use SymbolToSubscript with tensor of rank 3:
Use SymbolToSubscript with tensor of rank 4:
If the expression contains symbols with a capital C, the format for the other indexed symbols is the same as ith constant C[i]:
Use SymbolToSubscript with a nonlinear system of ordinary differential equations:
Use SymbolToSubscript with a system of partial differential equations:
Both the base and subscript in the output are symbols and inherit any existing definitions:
Applications (3)
Format a symbolic polynomial:
Format a symbolic matrix:
Use SymbolToSubscript and TeXForm:
Define a function for making a Vandermonde matrix:
Format a Vandermonde matrix:
The SymbolToSubscript command allows TeXForm to be used correctly when we have expressions with subscripts that are written as symbols:
Possible Issues (2)
Before getting the subscript format, SymbolToSubscript separates the expression x1y2 as {“x”,“1y2”}, and then passes each part to input form using ToExpression. Therefore, with the expression x1y2 we get xy2 instead x1y2:
To handle the above problem, SymbolToSubscript has the ToStringFormat option:
![ResourceFunction["SymbolToSubscript", ResourceVersion->"1.1.0"][{Sin[t], Cos[x], Tan[s], Cot[x1], BesselJ[0, x1[t] + x2[t]], Csch[(x^(m - 2) - x3) (x^(n + 1) + x2)]}]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/1-1-0/15465a063855c5f3.png)
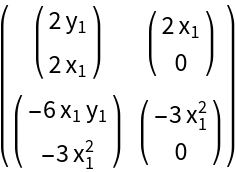
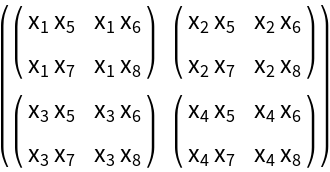
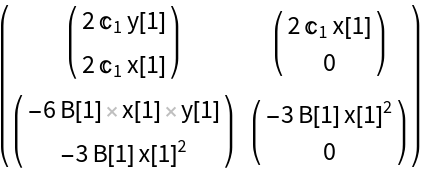
![ResourceFunction["SymbolToSubscript"]@{\!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(u1[t, x]\)\) == \!\(
\*SubscriptBox[\(\[PartialD]\), \(x\)]\((\((u2[t, x] - 1)\)\
\*SubscriptBox[\(\[PartialD]\), \(x\)]u1[t, x])\)\) + (16 x t - 2 t - 16 (u2[t, x] - 1)) (u1[t, x] - 1) + 10 x E^(-4 x), \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(u2[t, x]\)\) == \!\(
\*SubscriptBox[\(\[PartialD]\), \({x, 2}\)]\(u2[t, x]\)\) + \!\(
\*SubscriptBox[\(\[PartialD]\), \(x\)]\(u1[t, x]\)\) + 4 u1[t, x] - 4 + x^2 - 2 t - 10 t E^(-4 x)}](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/1-1-0/13acca44cd2b020e.png)
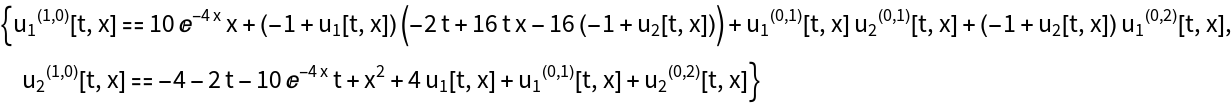
![polynomial[var_Symbol, coeff_Symbol, n_Integer?NonNegative] := Total[Array[
Times[ToExpression[
ToString[coeff] <> ToString[FromDigits[{n - ##}]]], var^#] &, n + 1, 0]]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/1-1-0/10ac20804cc0c880.png)
![Row[Map[MatrixForm, MapAt[Map[ResourceFunction["SymbolToSubscript"], #] &, ConstantArray[Matrix[x, {5, 5}], 2], {2}]], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/1-1-0/26561545f3582fc4.png)
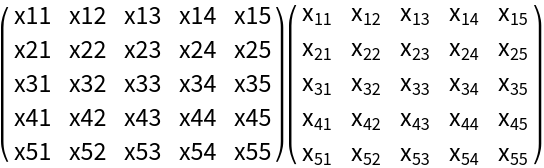
![Row[Map[MatrixForm, MapAt[ResourceFunction["SymbolToSubscript"][#] &, ConstantArray[Matrix[x, {5, 5}], 2], {2}]], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/1-1-0/511b956e8c2cf995.png)
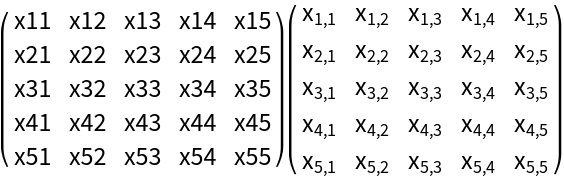

![VandermondeMatrix[symbol_Symbol, n_Integer?Positive] := Map[ToExpression, Array[(ToString[symbol] <> ToString[#1])^(#2 - 1) &, ConstantArray[n, 2]], {-1}]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/1-1-0/71beeb874c2103f1.png)
![Row[Map[MatrixForm, MapAt[Map[ResourceFunction["SymbolToSubscript"], #] &, ConstantArray[VandermondeMatrix[x, 5], 2], {2}]], " "]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/1-1-0/610f0632ad7dc26d.png)

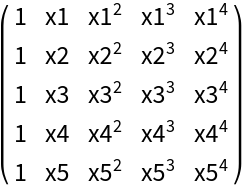

![polynomial[var_Symbol, coeff_Symbol, n_Integer?NonNegative] := Total[Array[
Times[ToExpression[
ToString[coeff] <> ToString[FromDigits[{n - ##}]]], var^#] &, n + 1, 0]]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/1-1-0/343be06506b4a214.png)


![ResourceFunction["SymbolToSubscript"]@
ResourceFunction[
"SolutionRulesToFunctions"][\[Theta][t] -> \[Theta]0 + t \[Omega]0 + (g t^2 Sin[\[Alpha]])/(3 R)]](https://www.wolframcloud.com/obj/resourcesystem/images/53c/53c18bc3-6bed-4e6d-b6a7-aebbfd3451ac/1-1-0/749f132ac41814f9.png)