Quantum Basis and Quantum State (19)
In order to use QuantumBasis, one gives dimension information as arguments, which will be interpreted as the computational basis. Alternatively, an association can be given with the basis name as the key and the corresponding basis elements as the values.
Define a 2D quantum basis (computational):
Given a basis of dimension n, the basis elements will be indexed by the key 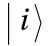 with :
with :
Use QuantumBasis[n,m] to define a basis for qudits of dimension (for which the overall dimension will be ). For example, define a 2–2–2 dimensional quantum basis (with three qubits):
Use QuantumBasis[{n1,n2,…,nm}] to define an -dimensional Hilbert space of qudits as a list. For example, define a 3×5 dimensional quantum basis (with two qudits):
A basis can also be defined as an association with the basis element names as keys and the corresponding vectors as values:
There are many 'named' bases built into the quantum framework, including "Computational", "PauliX", "PauliY", "PauliZ", "Fourier", "Identity", "Schwinger", "Pauli", "Dirac" and "Wigner" bases:
After a basis object has been defined, it is straightforward to construct quantum states and operators. A quantum state is represented by a QuantumState object and a quantum operator is represented by QuantumOperator.
A pure quantum state is represented as a vector for which the elements are amplitudes. The corresponding basis should be given in this format: QuantumState[arg1,arg2], where arg1 specifies amplitudes or the density matrix, and arg2 specifies the basis. With no basis specified, the default basis will be the computational basis, the dimension of which depends on the amplitude vector given in arg1.
Note that we use the big endian convention, such that qubits are labelled left-to-right, starting with one. For example, the decimal representation of (which means ⊗⊗3) is . Additionally, for the eigenvalues of Pauli-Z, we have:
We shall denote the eigenstate {1,0} by (which corresponds to +1 eigenvalue), and {0,1} by (corresponding to the eigenvalue -1)
Define a pure 2-dimensional quantum state (qubit) in the Pauli-X basis:
If the basis is not specified, the default is the computational basis of dimensions ( qubits):
If the vector has more than 2 elements, it is interpreted as an -qubit state, unless the dimension is specified. If fewer than amplitudes are specified, right-padding is applied to reach the 'ceiling':
Here is the same amplitude vector, but this time with the dimension specified:
Binary strings can be also used as inputs:
Many 'named' states are available through the framework:
Using associations, one can create a superposition of states, where the keys are lists of corresponding indexes and the values are amplitudes.
Create a superposition of 3 qubits (i.e., QuantumBasis[2,3]) as 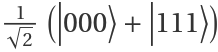 :
:
A superposition can also be created by simply adding two quantum state objects. For example, the previous state can also be constructed as follows:
With a built-in basis specified, amplitudes correspond to the basis elements. For example, use the Bell basis:
A state can also be defined by inputting a density matrix:
For pure states, one can get the corresponding normalized state vector:
Define a generic Bloch vector:
Test to see if it is a mixed state:
Calculate its Von Neumann entropy:
Compute its purity:
Note that one can directly use a Bloch vector as an input:
Test to see if a matrix is positive semidefinite:
A matrix that is not positive semidefinite cannot be a density matrix in standard quantum mechanics (with some exceptional cases, such as ZX formalism). Here is the result when we attempt to define a state using such a matrix:
When a matrix is given as input, but no basis is given, the default basis will be computational:
Using , define a quantum state in a 2–4 dimensional basis (and note the number of qudits):
Define a quantum state in 8D Hilbert space (with one 8-dimensional qudit only):
One can also define a state in a given basis, and then transform it into a new basis. For example, transform 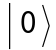 , the computational basis, into the Pauli-X basis {,}:
, the computational basis, into the Pauli-X basis {,}:
Return the amplitudes:
Note that the states are the same, but defined in different bases:
One can use QuantumTensorProduct to construct different states or operators. Create a tensor product of a + state with three qubits 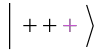 :
:
Another way of defining 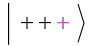 is to first define a basis and then assign amplitudes:
is to first define a basis and then assign amplitudes:
Quantum Operators (10)
Quantum operators can be defined by a matrix or by specifying eigenvalues with respect to a QuantumBasis. Additionally, there are many built-in named operators that can be used.
Define a Pauli-X operator:
Apply a Pauli-X operator to a symbolic state 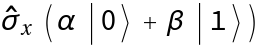 :
:
Test to see if the application of the Pauli-X operator yields the correct state:
Apply the Hadamard operator 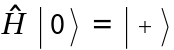 :
:
Test to see if the application of the Hadamard operator yields the correct state:
One can also compose operators. Here's a composition of two Hadamard operators and one Pauli-Z operator:
Check the relation  :
:
Multi-qubit operators can take specific orders.
For instance, first define the state +:
Then, apply a Pauli-X operator on the second qubit only (by defining an order for the operator):
Test the result:
For multi-qudit cases, one can define an order or construct the operator using QuantumTensorProduct. For example:
Generalize Pauli matrices to higher dimensions:
Convert to matrix form:
Generalize the Hadamard operator to more qubits:
Test that the Hadamard operator can be constructed as a tensor product :
One can define a "ControlledU" operator with specific target and control qudits:
Return the control and target qudits:
Get the action of the operator (T-controlled (1, 2)) on :
Note that "CT" is also a 'named' controlled operator in our framework:
One can create a new operator by performing some mathematical operations (e.g., exponential, fraction power, etc.) on a quantum operator:
Show that the result is the same as a rotation operator around x:
Get the fractional power of the NOT operator:
Quantum partial tracing, distance and entanglement (4)
In our framework, there are some functionalities to explore the quantum distance, entanglement monotones, partial tracing and other useful feature.
Trace out the second subsystem in a 2-qubit state:
A partial trace can also be applied to QuantumBasis:
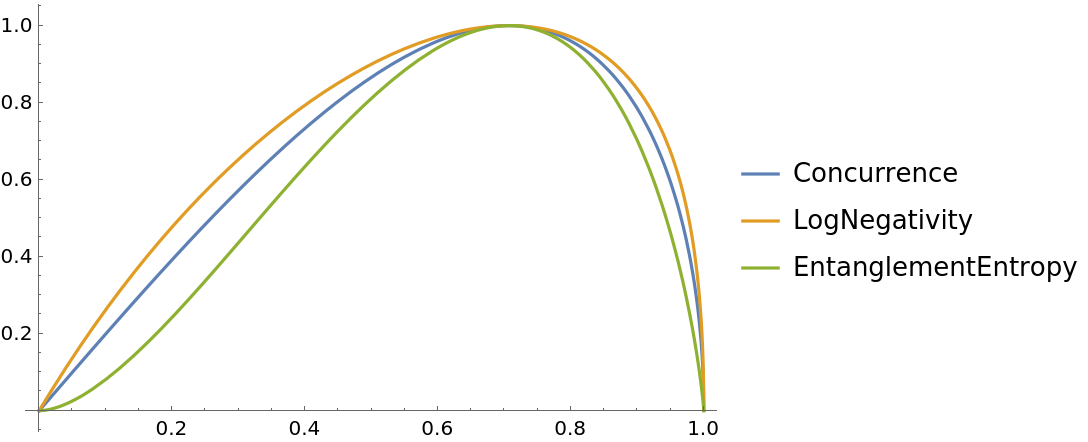
There are several metrics by which one can measure entanglement between two qudits, such as concurrence, entanglement entropy, negativity, etc. The calculation of entanglement measure is represented by the QuantumEntanglementMonotone function.
Plotting various entanglement measure for the state 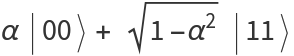 :
:
To know whether a state is entangled or separable without computing its measure, use QuantumEntangledQ.
Check whether subsystems 1 and 3 are entangled in the "W" state:
In quantum information, there exist notions of distance between quantum states, such as fidelity, trace distance, Bures angle, etc. One can use QuantumDistance to compute the distance between two quantum states with various metrics.
Measure the trace distance between a pure state and a mixed state:
Quantum Circuits (4)
One may create a list of QuantumOperator and/or QuantumMeasurementOperator objects to build a quantum circuit, which can be represented as a QuantumCircuitOperator object.
Construct a quantum circuit that includes a controlled Hadamard gate:
The wire labels can be customized:
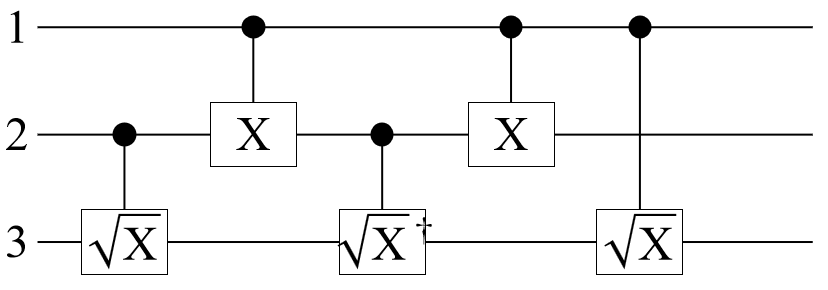
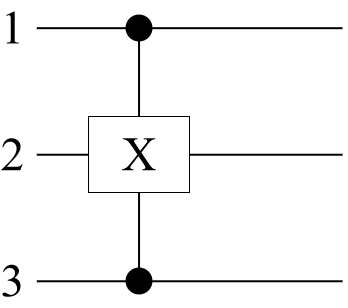
Construct a Toffoli gate as a circuit:
Show that the circuit is the same as the Toffoli gate:
One can define more than one control and target qubit:
Define the unitary operator and controlled-u operator:
Return the control qubits:
Return the target qubits:
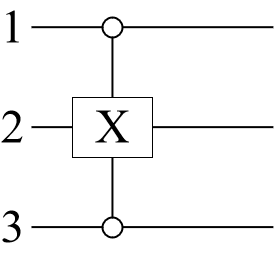
Define the control-0 qubits:
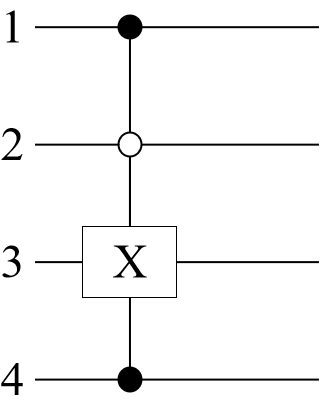
Define a combination of control-0 and control-1 qubits:
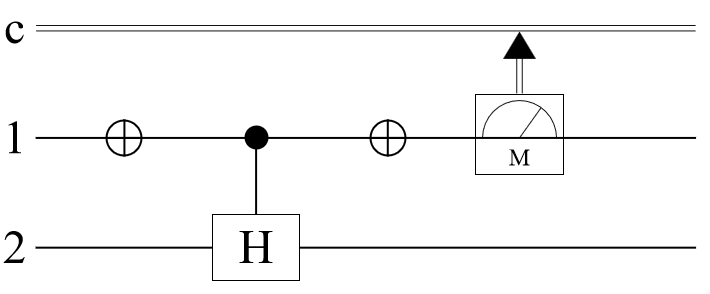
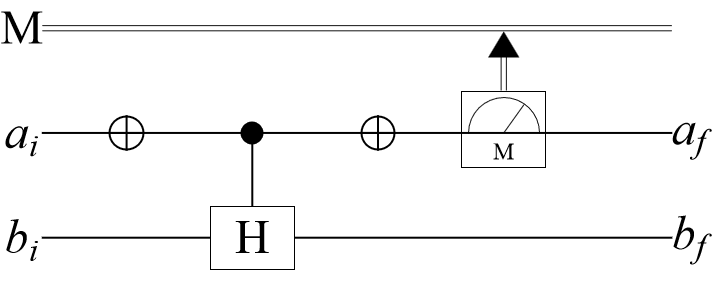
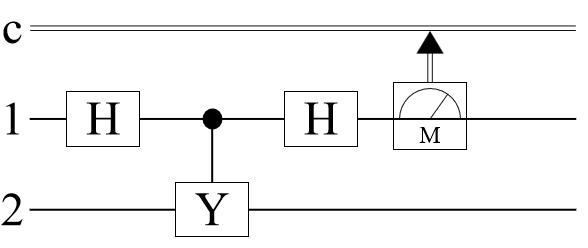
Measurement operators can also be added to a quantum circuit. For a single-qubit unitary operator with eigenvalues ±1, a measurement of can be implemented in the following circuit. (Note that here, Pauli-Y is considered a operator):
Applying the circuit operators to a quantum state results in a quantum measurement:
Calculate the state of the second qubit after the measurement by tracing over the first qubit:
The post-measurement states of the second qubit should be the same as the Pauli-Y eigenstates.
Quantum Protocols & Algorithms (59)
Superdense coding (5)
Alice wants to send Bob two classical bits: 00, 01, 10, or 11. She can do so by using a single qubit if her qubit and Bob's are initially prepared as Bell states:
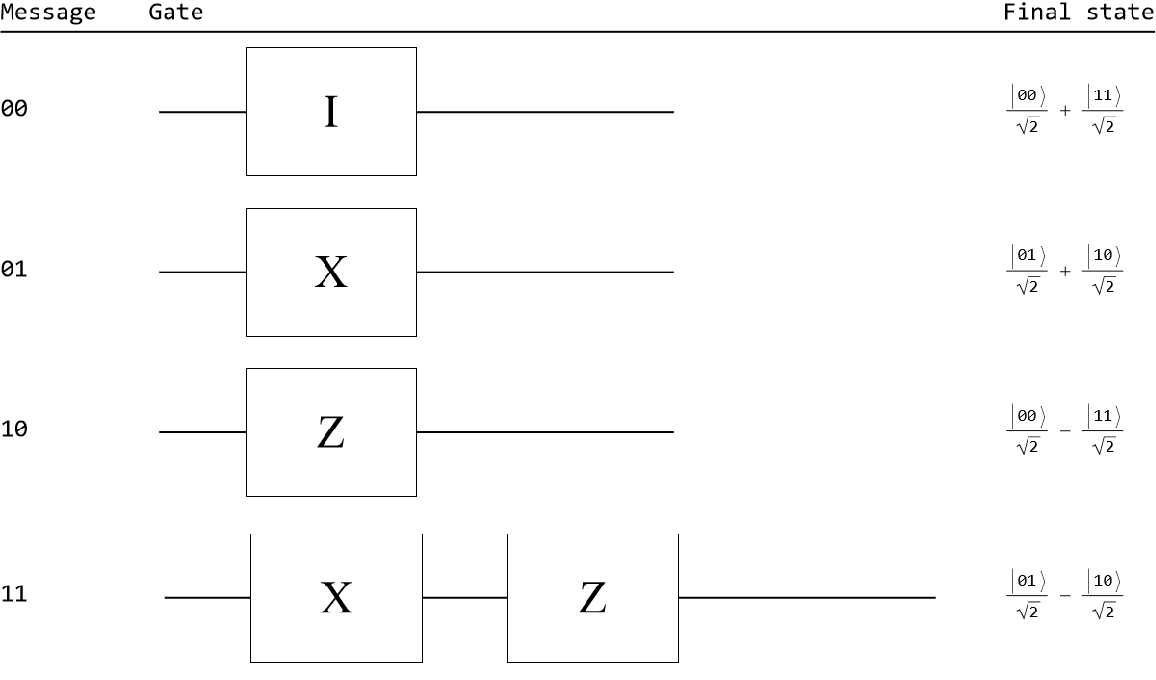
Depending on Alice's intended message, she will perform the following operations on her qubit:
1. To send 00, she does nothing.
2. To send 01, she applies the X-gate.
3. To send 10, she applies the Z-gate.
4. To send 11, she applies the X-gate and then the Z-gate.
Such operations can be represented as circuits, each with a final state resulting from application of its respective gate(s) to the initial Bell state:
Next, Alice sends her qubit to Bob through a quantum channel. If Bob performs a Bell measurement on his qubits, he receives Alice's message.
Alice's 'messaging' with Bob can be fully implemented in a quantum circuit using two ancillary qubits. In the circuit, the 1st qubit is Alice's, the 2nd one is Bob's, and the 3rd and the 4th are the ancillary qubits. (Note that Alice sends her qubit to Bob and Bob performs a measurement on qubits 1 and 2):
Define an initial state as , where is the code that Alice wants to send Bob, which is encoded in two ancillary qubits (qubits 3 and 4).
Run the state through the circuit and return the outcome probabilities:
For each case, Bob finds Alice's code with probability 1.
Quantum teleportation (4)
Quantum teleportation is the reverse of superdense coding. Here, one wants to teleport a generic unknown quantum bit. Suppose that Alice wants to send a qubit (qubit 1) to Bob. To implement a quantum circuit for teleporting a qubit, Alice and Bob share an entangled state (qubits 2 and 3). Qubits 1 and 2 represent Alice's system, while qubit 3 is Bob's. The goal is to transfer the state of Alice's first qubit to Bob's qubit.
Set up a circuit:
The state to be teleported is =α+β, where α and β are unknown amplitudes. The input state of the circuit is as follows:
Given the result of Alice's measurement on the first and second qubits, get the post-measurement states:
Regardless of measurement results, the state of the third qubit is the same state as the original first qubit =α+β (with only a normalization difference). Trace out the first and second qubits and compare the reduced state of qubit 3 only:
Deutsch–Jozsa algorithm (3)
Alice wants to determine if a Boolean function , used by Bob, is constant for all values of or balanced (where is an -digit binary number between 0 and -1). Consider a balanced implementation of for n=2 as follows: , , , meaning ⊻.
Given n=4, show that XOR is balanced:
Consider the case where Alice stores her query in a 2-qubit system, denoted by qubit 1 and qubit 2. Bob will store the answer in the 3rd qubit (the answer qubit). After Bob performs the oracle, Alice measures her qubits. If she gets anything other than , then the oracle is a balanced function.
Implement the algorithm:
Get the action of the quantum circuit as a measurement of the initial state:
The measurement indicates that the oracle is a balanced function.
Bernstein–Vazirani algorithm (3)
The goal of Bernstein–Vazirani algorithm is to find a secret string bit as s using the action of a Bernstein–Vazirani oracle (i.e., which should be treated as a black box) which is defined by this transformation: → with the index register state of n-qubits, and the state of an ancillary qubit carrying the result.
Bernstein–Vazirani oracle for the secret bit of 101:
Bernstein–Vazirani circuit for the secret bit of 101:
As expected, the only measurement outcome corresponds to the secret bit-string:
Grover's search algorithm (14)
The goal of Grover's search algorithm is to find solutions of a Boolean function . This can be done using the named-circuits or oracles in our quantum framework.
The action of a Boolean oracle is defined by this transformation: → with the index register state of n-qubits, and the state of an ancillary qubit carrying the result of Boolean function f(x); meaning if = then it will be if x is a solution of f(x), and no change if not.
Define a Boolean function of 3-SAT with 5 clauses:
Truth table of above Boolean function:
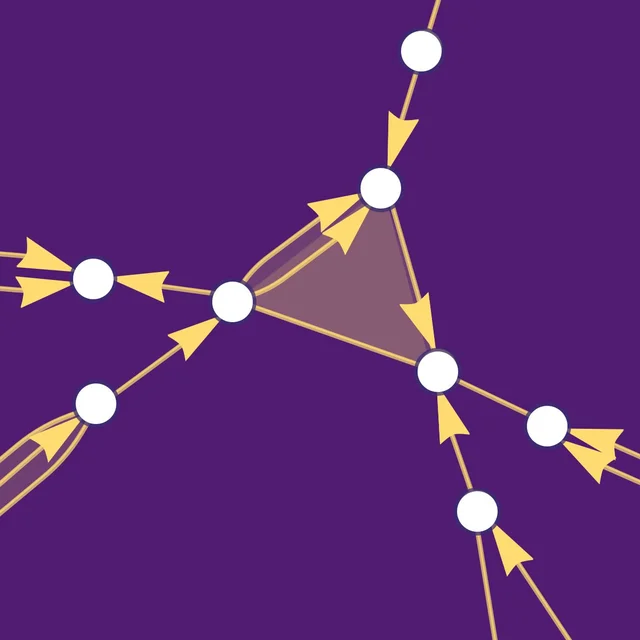
Corresponding oracle's quantum circuit:
The diagram of oracle:
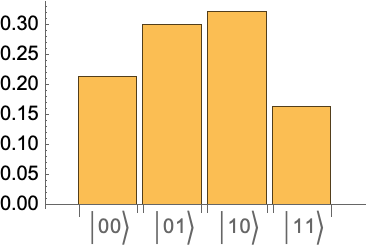
We shall prepare the 4-qubit in above circuit (ie the ancillary qubit) is 0 state, and then other qubits (1-3) in the index register states. To compare with above truth table, we will create the index register states |x> in the order |2n-1> down to |0:
Create a list with elements {|x>,|q⊕f(x)}:
The action of a phase oracle can be defined as the following transformation: with the index register state of n-qubits:
The diagram of oracle:
Create a list with elements {|x>,(-1)f(x)|x>}:
Generate the corresponding Grover circuit using a Boolean oracle:
Generate a Grover circuit using the phase oracle for a Boolean function:
Given a Grover-phase circuit for a Boolean function, calculate the probability of success of the algorithm:
Calculate the success probability after each iteration (note 111 is the solution of the Boolean function):
Plot the success probability:
which, as expected, follows the formula for the probability of success 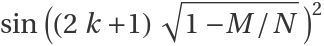 where M is number of correct solutions out of total N after k steps
where M is number of correct solutions out of total N after k steps
Quantum phase estimation (5)
The Quantum phase estimation algorithm solves the problem of finding in the eigenvalue equation = where is a unitary operator. The inputs of the algorithm are qubits at the initial state 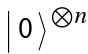 . The output is
. The output is  .
We will consider a phase shift as the unitary operator where we aim to find the phase θ:
.
We will consider a phase shift as the unitary operator where we aim to find the phase θ:
To specify the corresponding quantum circuit, one can use the built-in circuit "PhaseEstimation" that takes two input arguments: a unitary operator U, and an integer n. The integer n specifies the number of qubits and controlled-Uj operators in the circuit, with j=0,1,…,n-1. The accuracy of phase estimation and the success probability depends on n:
Return the corresponding measurement, with all qubits prepared in state:
Given the outcome with the largest probability, estimate the phase:
As expected, it is a rough estimate, since we picked a small value for n. If one increases n, with a higher probability, one can get a better estimate of the phase.
Estimate the phase (the expected value is 1/5=0.2) for n=6:
Shor's algorithm
Shor's algorithm is an algorithm that can factorize a large number using a quantum computation. Given an integer , Shor's algorithm can return its factors and such that . This task is difficult for a classical computer if is large. The algorithm involves three main steps: classical pre-processing, quantum order-finding, and classical post-processing.
1. Classical preprocessing
- If is even, return 2 and /2.
- If is odd, pick a random number .
- Compute the greatest common divisor (GCD) of a and N. If GCD(, )!=1, return a and /a.
- If GCD(, )= 1, proceed to the order-finding algorithm.
2. Quantum order-finding
- Initialize a 2n qubit register (for ) in the state .
- Apply Hadamard gates to the first qubits.
- Apply modular exponentiation gate
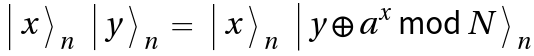 , where the subscript indicates the number of qubits.
, where the subscript indicates the number of qubits.
- Apply the inverse quantum Fourier transform to the first qubits.
- Measure the first qubits in the computational basis.
3. Classical post-processing
- Let s be the integer representation of the measurement outcome. Compute the order r of axmod N by finding the solutions to j(/r) = s, where j is an integer.
- If is odd or choose a different a and repeat the process.
- Otherwise, at least one of or 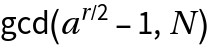 is a nontrivial factor of .
is a nontrivial factor of .
The quantum circuit used for quantum order-finding can be schematically illustrated as the following (n =3). (Note that U4 is the modular exponent gate):
Currently, the specific gate implementation of the modular exponentiation for arbitrary and a is unknown. However, there are some specific cases that have been studied. In the following, consider the implementation of quantum order-finding for (, a) = (15, 7) that has been demonstrated in experiments. Although one needs 8 qubits to factor 15 in general, by choosing a specific a, it is possible to use only 7 qubits (3 register, 4 ancilla).
Prepare the quantum order-finding circuit for (, a) = (15, 7):
Initialize the state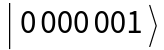 :
:
Apply the Shor circuit to the initial state:
In decimal notation, the possible states are: 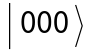 ,
, 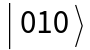 ,
, 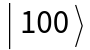 , and
, and 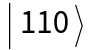 . If one obtains
. If one obtains 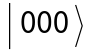 , one must repeat the protocol. Otherwise:
, one must repeat the protocol. Otherwise:
Outcome: |2〉 → j(8/r) = 2 (j, r) = (1, 4)
p=GCD[(74/2+1) ,15] = 5 and q= GCD[(74/2-1),15] = 3
Outcome: |4〉 → j(8/r) = 4 (j, r) = (1, 2)
p= GCD[(72/2+1),15] = 1 and q= GCD[(72/2-1),15] = 3
Outcome: |6〉 → j(8/r) = 6 (j, r) = (3, 4)
p=GCD[(74/2+1) ,15] = 5 and q= GCD[(74/2-1),15] = 3
Thus, with 0.75 probability, one can find at least one nontrivial factor of 15.
Quantum Key Distribution: BB84 scheme (11)
As an example of a quantum key distribution (QKD), consider the BB84 protocol. Alice generates random bits and for each, randomly chooses either a Z-basis or X-basis of measurement. Consider a sequence of 9 bits:
Depending on her choice of bit and base, she follows the following protocol for sending a qubit to Bob:
With Alice's bits and bases having been generated randomly, she will send Bob these qubits:
Bob randomly generates a sequence of either Z-bases or X-bases of measurement:
Thus, Bob applies the following measurement operators on the qubits he recieved from Alice:
Post-measurement, it is the case that, whenever Bob's measurement basis is not the same as Alice's, he gets two random results:
Return one possible realization of Bob' s series of measurements (noting that some results will be consistent and other random, depending on Alice' s qubit and Bob's measurement):
Bob assigns the bit 0 whenever he gets or , and the bit 1 for or :
Finally, Alice and Bob publicly share with each other the measurement basis that they used (in other words, they conduct a classical communication). If the basis is same, they each keep the bit; if not, they each disregard the corresponding bit. (Note that each does so separately, and each one obtains a secret key, which will be the same as the other's):
Alice and Bob now share a secret key. Note that the key length is less than the number of qubits Alice sent to Bob (because Bob picks the measurement basis randomly, and he might not get the same outcome as Alice). Alice can keep sending Bob qubits until they reach a desired length. This can be implemented as follows:
For example, the key length is set to 5 bits below:
![]() with :
with :![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/08247e84-c52b-40da-b087-6e1dc0a40202"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/4dbf430f79a26c55.png)




![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/4a5347ec-fda1-43e1-99da-baf387d819f5"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/23fdeae244913efd.png)
![]() :
:
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/8e06a0b4-cd95-43ab-9ec0-8b2edbc289ae"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/73c934b7f0a74c46.png)
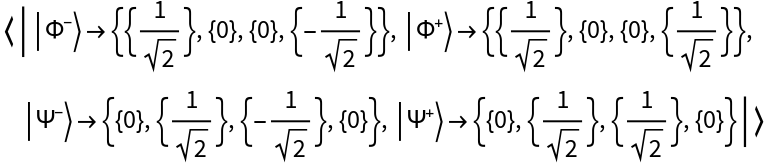





![m = RandomComplex[{-1 - I, 1 + I}, {8, 8}];
\[Rho] = ConjugateTranspose[m] . m;
state = InterpretationBox[FrameBox[TagBox[TooltipBox[PaneBox[GridBox[List[List[GraphicsBox[List[Thickness[0.015384615384615385`], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[19.29685914516449`, 56.875006675720215`], List[32.49997329711914`, 64.49218791723251`], List[45.70308744907379`, 56.875006675720215`], List[32.49997329711914`, 49.257825434207916`], List[19.29685914516449`, 56.875006675720215`]], List[List[21.328107476234436`, 56.875006675720215`], List[32.49997329711914`, 63.32422015108166`], List[43.671839118003845`, 56.875006675720215`], List[32.49997329711914`, 50.42579283714326`], List[21.328107476234436`, 56.875006675720215`]], List[List[33.00778537988663`, 33.26174482703209`], List[33.00778537988663`, 48.496107310056686`], List[46.21089953184128`, 56.113288551568985`], List[46.21089953184128`, 40.87892606854439`], List[33.00778537988663`, 33.26174482703209`]]]]], List[FaceForm[RGBColor[0.7019607843137254`, 0.6039215686274509`, 0.788235294117647`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[31.992161214351654`, 33.26174482703209`], List[18.789047062397003`, 40.87892606854439`], List[18.789047062397003`, 56.113288551568985`], List[31.992161214351654`, 48.496107310056686`], List[31.992161214351654`, 33.26174482703209`]]]]], List[FaceForm[RGBColor[0.5372549019607843`, 0.403921568627451`, 0.6745098039215687`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[17.77342289686203`, 8.886764854192734`], List[4.570308744907379`, 16.503946095705032`], List[4.570308744907379`, 31.73830857872963`], List[17.77342289686203`, 24.12112733721733`], List[17.77342289686203`, 8.886764854192734`]], List[List[16.757798731327057`, 10.664107143878937`], List[5.585932910442352`, 17.113319045306525`], List[5.585932910442352`, 29.960966289043427`], List[16.757798731327057`, 23.511754387615838`], List[16.757798731327057`, 10.664107143878937`]], List[List[31.484349131584167`, 32.50002670288086`], List[18.281234979629517`, 40.11720794439316`], List[5.078120827674866`, 32.50002670288086`], List[18.281234979629517`, 24.88284546136856`], List[31.484349131584167`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.6352941176470588`, 0.7333333333333333`, 0.8313725490196079`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[31.992161214351654`, 31.73830857872963`], List[18.789047062397003`, 24.12112733721733`], List[18.789047062397003`, 8.886764854192734`], List[31.992161214351654`, 16.503946095705032`], List[31.992161214351654`, 31.73830857872963`]]]]], List[FaceForm[RGBColor[0.2901960784313726`, 0.40784313725490196`, 0.5764705882352941`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[47.22652369737625`, 8.886764854192734`], List[47.22652369737625`, 24.12112733721733`], List[60.4296378493309`, 31.73830857872963`], List[60.4296378493309`, 16.503946095705032`], List[47.22652369737625`, 8.886764854192734`]], List[List[48.242147862911224`, 10.664107143878937`], List[48.242147862911224`, 23.511754387615838`], List[59.41401368379593`, 29.960966289043427`], List[59.41401368379593`, 17.113319045306525`], List[48.242147862911224`, 10.664107143878937`]], List[List[33.515597462654114`, 32.50002670288086`], List[46.718711614608765`, 40.11720794439316`], List[59.921825766563416`, 32.50002670288086`], List[46.718711614608765`, 24.88284546136856`], List[33.515597462654114`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.6`, 0.6`, 0.37254901960784315`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[33.00778537988663`, 31.73830857872963`], List[33.00778537988663`, 16.503946095705032`], List[46.21089953184128`, 8.886764854192734`], List[46.21089953184128`, 24.12112733721733`], List[33.00778537988663`, 31.73830857872963`]]]]], List[FaceForm[RGBColor[0.396078431372549`, 0.6039215686274509`, 0.30196078431372547`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[5.585932910442352`, 35.03908711671829`], List[5.585932910442352`, 47.88673242330583`], List[16.757798731327057`, 54.33594626188278`], List[16.757798731327057`, 41.488300955295244`], List[5.585932910442352`, 35.03908711671829`]], List[List[4.570308744907379`, 33.26174482703209`], List[4.570308744907379`, 48.496107310056686`], List[17.77342289686203`, 56.113288551568985`], List[17.77342289686203`, 40.87892606854439`], List[4.570308744907379`, 33.26174482703209`]], List[List[60.4296378493309`, 33.26174482703209`], List[47.22652369737625`, 40.87892606854439`], List[47.22652369737625`, 56.113288551568985`], List[60.4296378493309`, 48.496107310056686`], List[60.4296378493309`, 33.26174482703209`]], List[List[59.41401368379593`, 35.03908711671829`], List[48.242147862911224`, 41.488300955295244`], List[48.242147862911224`, 54.33594626188278`], List[59.41401368379593`, 47.88673242330583`], List[59.41401368379593`, 35.03908711671829`]], List[List[19.29685914516449`, 8.125046730041504`], List[32.49997329711914`, 15.742227971553802`], List[45.70308744907379`, 8.125046730041504`], List[32.49997329711914`, 0.5078654885292053`], List[19.29685914516449`, 8.125046730041504`]], List[List[21.328107476234436`, 8.125046730041504`], List[32.49997329711914`, 14.574258631469093`], List[43.671839118003845`, 8.125046730041504`], List[32.49997329711914`, 1.6758348286139153`], List[21.328107476234436`, 8.125046730041504`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[7.109369158744812`, 32.50002670288086`], List[7.109369158744812`, 31.097747524374427`], List[5.972591313425198`, 29.960966289043427`], List[4.570308744907379`, 29.960966289043427`], List[3.168024481383867`, 29.960966289043427`], List[2.0312483310699463`, 31.097747524374427`], List[2.0312483310699463`, 32.50002670288086`], List[2.0312483310699463`, 33.90230975568602`], List[3.168024481383867`, 35.03908711671829`], List[4.570308744907379`, 35.03908711671829`], List[5.972591313425198`, 35.03908711671829`], List[7.109369158744812`, 33.90230975568602`], List[7.109369158744812`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 56.36719459295273`], List[20.82029539346695`, 54.96491250872225`], List[19.683518032434677`, 53.828134179115295`], List[18.281234979629517`, 53.828134179115295`], List[16.878951926824357`, 53.828134179115295`], List[15.742174565792084`, 54.96491250872225`], List[15.742174565792084`, 56.36719459295273`], List[15.742174565792084`, 57.76947716147055`], List[16.878951926824357`, 58.90625500679016`], List[18.281234979629517`, 58.90625500679016`], List[19.683518032434677`, 58.90625500679016`], List[20.82029539346695`, 57.76947716147055`], List[20.82029539346695`, 56.36719459295273`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 40.625020027160645`], List[20.82029539346695`, 39.222736974355485`], List[19.683518032434677`, 38.08595961332321`], List[18.281234979629517`, 38.08595961332321`], List[16.878951926824357`, 38.08595961332321`], List[15.742174565792084`, 39.222736974355485`], List[15.742174565792084`, 40.625020027160645`], List[15.742174565792084`, 42.027303079965804`], List[16.878951926824357`, 43.16408044099808`], List[18.281234979629517`, 43.16408044099808`], List[19.683518032434677`, 43.16408044099808`], List[20.82029539346695`, 42.027303079965804`], List[20.82029539346695`, 40.625020027160645`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 24.375033378601074`], List[20.82029539346695`, 22.97275420009464`], List[19.683518032434677`, 21.83597296476364`], List[18.281234979629517`, 21.83597296476364`], List[16.878951926824357`, 21.83597296476364`], List[15.742174565792084`, 22.97275420009464`], List[15.742174565792084`, 24.375033378601074`], List[15.742174565792084`, 25.777316431406234`], List[16.878951926824357`, 26.914093792438507`], List[18.281234979629517`, 26.914093792438507`], List[19.683518032434677`, 26.914093792438507`], List[20.82029539346695`, 25.777316431406234`], List[20.82029539346695`, 24.375033378601074`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 8.63285881280899`], List[20.82029539346695`, 7.230591257198739`], List[19.683518032434677`, 6.093798398971558`], List[18.281234979629517`, 6.093798398971558`], List[16.878951926824357`, 6.093798398971558`], List[15.742174565792084`, 7.230591257198739`], List[15.742174565792084`, 8.63285881280899`], List[15.742174565792084`, 10.035130242717969`], List[16.878951926824357`, 11.171919226646423`], List[18.281234979629517`, 11.171919226646423`], List[19.683518032434677`, 11.171919226646423`], List[20.82029539346695`, 10.035130242717969`], List[20.82029539346695`, 8.63285881280899`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 48.75001335144043`], List[35.03903371095657`, 47.34773029863527`], List[33.90225247562557`, 46.210952937603`], List[32.49997329711914`, 46.210952937603`], List[31.09769024431398`, 46.210952937603`], List[29.960912883281708`, 47.34773029863527`], List[29.960912883281708`, 48.75001335144043`], List[29.960912883281708`, 50.15229543567091`], List[31.09769024431398`, 51.28907376527786`], List[32.49997329711914`, 51.28907376527786`], List[33.90225247562557`, 51.28907376527786`], List[35.03903371095657`, 50.15229543567091`], List[35.03903371095657`, 48.75001335144043`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 32.50002670288086`], List[35.03903371095657`, 31.097747524374427`], List[33.90225247562557`, 29.960966289043427`], List[32.49997329711914`, 29.960966289043427`], List[31.09769024431398`, 29.960966289043427`], List[29.960912883281708`, 31.097747524374427`], List[29.960912883281708`, 32.50002670288086`], List[29.960912883281708`, 33.90230975568602`], List[31.09769024431398`, 35.03908711671829`], List[32.49997329711914`, 35.03908711671829`], List[33.90225247562557`, 35.03908711671829`], List[35.03903371095657`, 33.90230975568602`], List[35.03903371095657`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 16.25004005432129`], List[35.03903371095657`, 14.847760875814856`], List[33.90225247562557`, 13.710979640483856`], List[32.49997329711914`, 13.710979640483856`], List[31.09769024431398`, 13.710979640483856`], List[29.960912883281708`, 14.847760875814856`], List[29.960912883281708`, 16.25004005432129`], List[29.960912883281708`, 17.65232310712645`], List[31.09769024431398`, 18.789100468158722`], List[32.49997329711914`, 18.789100468158722`], List[33.90225247562557`, 18.789100468158722`], List[35.03903371095657`, 17.65232310712645`], List[35.03903371095657`, 16.25004005432129`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 56.36719459295273`], List[49.2577720284462`, 54.96491250872225`], List[48.1209907931152`, 53.828134179115295`], List[46.718711614608765`, 53.828134179115295`], List[45.316428561803605`, 53.828134179115295`], List[44.17965120077133`, 54.96491250872225`], List[44.17965120077133`, 56.36719459295273`], List[44.17965120077133`, 57.76947716147055`], List[45.316428561803605`, 58.90625500679016`], List[46.718711614608765`, 58.90625500679016`], List[48.1209907931152`, 58.90625500679016`], List[49.2577720284462`, 57.76947716147055`], List[49.2577720284462`, 56.36719459295273`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 40.625020027160645`], List[49.2577720284462`, 39.222736974355485`], List[48.1209907931152`, 38.08595961332321`], List[46.718711614608765`, 38.08595961332321`], List[45.316428561803605`, 38.08595961332321`], List[44.17965120077133`, 39.222736974355485`], List[44.17965120077133`, 40.625020027160645`], List[44.17965120077133`, 42.027303079965804`], List[45.316428561803605`, 43.16408044099808`], List[46.718711614608765`, 43.16408044099808`], List[48.1209907931152`, 43.16408044099808`], List[49.2577720284462`, 42.027303079965804`], List[49.2577720284462`, 40.625020027160645`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 24.375033378601074`], List[49.2577720284462`, 22.97275420009464`], List[48.1209907931152`, 21.83597296476364`], List[46.718711614608765`, 21.83597296476364`], List[45.316428561803605`, 21.83597296476364`], List[44.17965120077133`, 22.97275420009464`], List[44.17965120077133`, 24.375033378601074`], List[44.17965120077133`, 25.777316431406234`], List[45.316428561803605`, 26.914093792438507`], List[46.718711614608765`, 26.914093792438507`], List[48.1209907931152`, 26.914093792438507`], List[49.2577720284462`, 25.777316431406234`], List[49.2577720284462`, 24.375033378601074`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 8.63285881280899`], List[49.2577720284462`, 7.230591257198739`], List[48.1209907931152`, 6.093798398971558`], List[46.718711614608765`, 6.093798398971558`], List[45.316428561803605`, 6.093798398971558`], List[44.17965120077133`, 7.230591257198739`], List[44.17965120077133`, 8.63285881280899`], List[44.17965120077133`, 10.035130242717969`], List[45.316428561803605`, 11.171919226646423`], List[46.718711614608765`, 11.171919226646423`], List[48.1209907931152`, 11.171919226646423`], List[49.2577720284462`, 10.035130242717969`], List[49.2577720284462`, 8.63285881280899`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[62.968698263168335`, 32.50002670288086`], List[62.968698263168335`, 31.097747524374427`], List[61.83190540494115`, 29.960966289043427`], List[60.4296378493309`, 29.960966289043427`], List[59.027366419421924`, 29.960966289043427`], List[57.89057743549347`, 31.097747524374427`], List[57.89057743549347`, 32.50002670288086`], List[57.89057743549347`, 33.90230975568602`], List[59.027366419421924`, 35.03908711671829`], List[60.4296378493309`, 35.03908711671829`], List[61.83190540494115`, 35.03908711671829`], List[62.968698263168335`, 33.90230975568602`], List[62.968698263168335`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]]], List[Rule[BaselinePosition, Scaled[0.15`]], Rule[ImageSize, 10], Rule[ImageSize, List[Automatic, 35]]]], StyleBox[RowBox[List["QuantumState", " "]], Rule[ShowAutoStyles, False], Rule[ShowStringCharacters, False], Rule[FontSize, Times[0.9`, Inherited]], Rule[FontColor, GrayLevel[0.1`]]]]], Rule[GridBoxSpacings, List[Rule["Columns", List[List[0.25`]]]]]], Rule[Alignment, List[Left, Baseline]], Rule[BaselinePosition, Baseline], Rule[FrameMargins, List[List[3, 0], List[0, 0]]], Rule[BaseStyle, List[Rule[LineSpacing, List[0, 0]], Rule[LineBreakWithin, False]]]], RowBox[List["PacletSymbol", "[", RowBox[List["\"Wolfram/QuantumFramework\"", ",", "\"QuantumState\""]], "]"]], Rule[TooltipStyle, List[Rule[ShowAutoStyles, True], Rule[ShowStringCharacters, True]]]], Function[Annotation[Slot[1], Style[Defer[PacletSymbol["Wolfram/QuantumFramework", "QuantumState"]], Rule[ShowStringCharacters, True]], "Tooltip"]]], Rule[Background, RGBColor[0.968`, 0.976`, 0.984`]], Rule[BaselinePosition, Baseline], Rule[DefaultBaseStyle, List[]], Rule[FrameMargins, List[List[0, 0], List[1, 1]]], Rule[FrameStyle, RGBColor[0.831`, 0.847`, 0.85`]], Rule[RoundingRadius, 4]], PacletSymbol["Wolfram/QuantumFramework", "QuantumState"], Rule[Selectable, False], Rule[SelectWithContents, True], Rule[BoxID, "PacletSymbolBox"]][\[Rho]]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/2ea26991ce8328cb.png)



![]() , the computational basis, into the Pauli-X basis {,}:
, the computational basis, into the Pauli-X basis {,}:![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/0fa658ad-c8ca-4d57-9f95-f6d120186c10"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/12183f0d7152f99a.png)

![]() :
:![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/b24a139d-b5ad-4b49-b636-bef8efb11c03"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/23bcc0a169468154.png)
![]() is to first define a basis and then assign amplitudes:
is to first define a basis and then assign amplitudes:![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/baf4a364-5e72-4c21-a8e7-e0ea2f512760"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/36d99ace4708a248.png)
![]() :
:
![]() :
:
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/1979ae5e-76e7-4c79-9149-810183d1a973"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/0e45b110e43648bb.png)
![]() :
:![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/8b71e411-be7f-439f-971c-458c90bf9486"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/7f6d1e7125df1aff.png)

![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/f8ad6afd-1797-4fbc-8c37-029c2e7f4443"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/210b3c2a0934eca1.png)
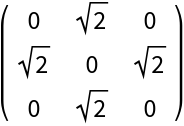
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/de17af73-f3dc-484d-a652-0398a841071d"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/08def04d72beed42.png)

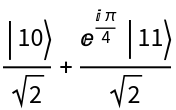
![]() , we get:
, we get:![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/55672c06-bc05-42ab-afe7-e36441af292e"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/367c5e4703c1ffef.png)

![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/691f6776-b3ea-48d8-95c9-e80d255372ca"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/211580bb5938ec2f.png)

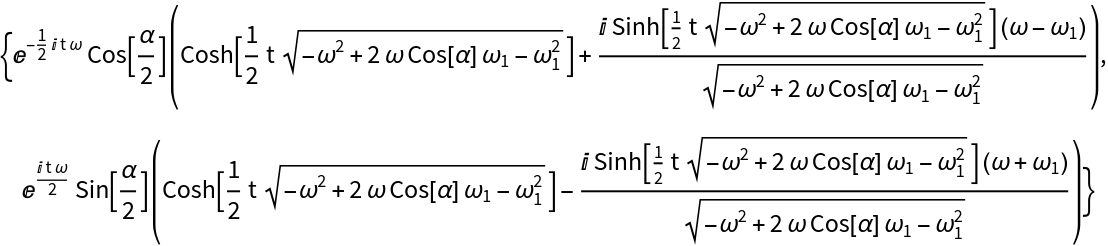
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9efc3d19-a7c2-4cda-bdbd-2a3c97305b32"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/78369825a38634cb.png)
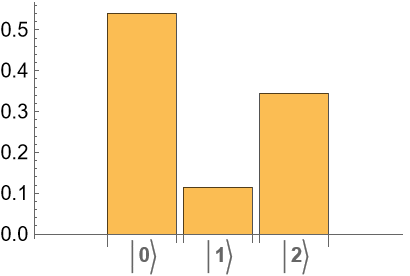
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/40dbad6c-aeb5-4c1b-b158-48c2b8a24a48"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/1d3cbd828ca39cae.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/135a0f15-c40c-4cf3-af8d-1933ad824c73"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/0ccbc6a1eb08d432.png)
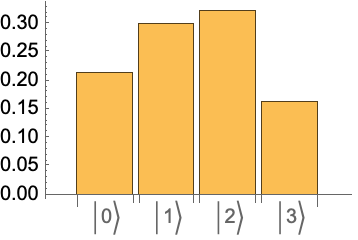
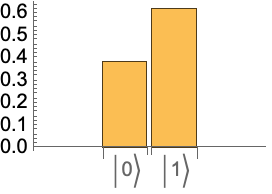
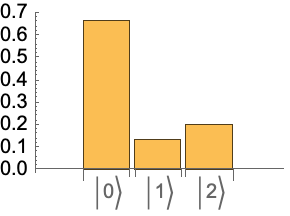
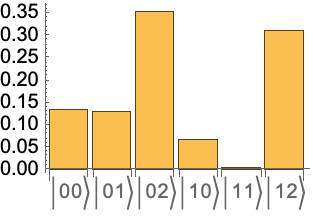
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/ce86ca93-ed8f-4ef0-8486-8656c4d389b8"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/4f76ff85c9296e0c.png)

![]() :
:![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/78dd29ec-6391-4481-850d-7e832b54da18"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/24706d67b7103c85.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/08dc3438-689d-4a58-8d07-ab8c8c7d105d"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/67a7511e4c30b132.png)
![AssociationMap[InterpretationBox[FrameBox[TagBox[TooltipBox[PaneBox[GridBox[List[List[GraphicsBox[List[Thickness[0.015384615384615385`], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[19.29685914516449`, 56.875006675720215`], List[32.49997329711914`, 64.49218791723251`], List[45.70308744907379`, 56.875006675720215`], List[32.49997329711914`, 49.257825434207916`], List[19.29685914516449`, 56.875006675720215`]], List[List[21.328107476234436`, 56.875006675720215`], List[32.49997329711914`, 63.32422015108166`], List[43.671839118003845`, 56.875006675720215`], List[32.49997329711914`, 50.42579283714326`], List[21.328107476234436`, 56.875006675720215`]], List[List[33.00778537988663`, 33.26174482703209`], List[33.00778537988663`, 48.496107310056686`], List[46.21089953184128`, 56.113288551568985`], List[46.21089953184128`, 40.87892606854439`], List[33.00778537988663`, 33.26174482703209`]]]]], List[FaceForm[RGBColor[0.7019607843137254`, 0.6039215686274509`, 0.788235294117647`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[31.992161214351654`, 33.26174482703209`], List[18.789047062397003`, 40.87892606854439`], List[18.789047062397003`, 56.113288551568985`], List[31.992161214351654`, 48.496107310056686`], List[31.992161214351654`, 33.26174482703209`]]]]], List[FaceForm[RGBColor[0.5372549019607843`, 0.403921568627451`, 0.6745098039215687`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[17.77342289686203`, 8.886764854192734`], List[4.570308744907379`, 16.503946095705032`], List[4.570308744907379`, 31.73830857872963`], List[17.77342289686203`, 24.12112733721733`], List[17.77342289686203`, 8.886764854192734`]], List[List[16.757798731327057`, 10.664107143878937`], List[5.585932910442352`, 17.113319045306525`], List[5.585932910442352`, 29.960966289043427`], List[16.757798731327057`, 23.511754387615838`], List[16.757798731327057`, 10.664107143878937`]], List[List[31.484349131584167`, 32.50002670288086`], List[18.281234979629517`, 40.11720794439316`], List[5.078120827674866`, 32.50002670288086`], List[18.281234979629517`, 24.88284546136856`], List[31.484349131584167`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.6352941176470588`, 0.7333333333333333`, 0.8313725490196079`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[31.992161214351654`, 31.73830857872963`], List[18.789047062397003`, 24.12112733721733`], List[18.789047062397003`, 8.886764854192734`], List[31.992161214351654`, 16.503946095705032`], List[31.992161214351654`, 31.73830857872963`]]]]], List[FaceForm[RGBColor[0.2901960784313726`, 0.40784313725490196`, 0.5764705882352941`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[47.22652369737625`, 8.886764854192734`], List[47.22652369737625`, 24.12112733721733`], List[60.4296378493309`, 31.73830857872963`], List[60.4296378493309`, 16.503946095705032`], List[47.22652369737625`, 8.886764854192734`]], List[List[48.242147862911224`, 10.664107143878937`], List[48.242147862911224`, 23.511754387615838`], List[59.41401368379593`, 29.960966289043427`], List[59.41401368379593`, 17.113319045306525`], List[48.242147862911224`, 10.664107143878937`]], List[List[33.515597462654114`, 32.50002670288086`], List[46.718711614608765`, 40.11720794439316`], List[59.921825766563416`, 32.50002670288086`], List[46.718711614608765`, 24.88284546136856`], List[33.515597462654114`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.6`, 0.6`, 0.37254901960784315`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[33.00778537988663`, 31.73830857872963`], List[33.00778537988663`, 16.503946095705032`], List[46.21089953184128`, 8.886764854192734`], List[46.21089953184128`, 24.12112733721733`], List[33.00778537988663`, 31.73830857872963`]]]]], List[FaceForm[RGBColor[0.396078431372549`, 0.6039215686274509`, 0.30196078431372547`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[5.585932910442352`, 35.03908711671829`], List[5.585932910442352`, 47.88673242330583`], List[16.757798731327057`, 54.33594626188278`], List[16.757798731327057`, 41.488300955295244`], List[5.585932910442352`, 35.03908711671829`]], List[List[4.570308744907379`, 33.26174482703209`], List[4.570308744907379`, 48.496107310056686`], List[17.77342289686203`, 56.113288551568985`], List[17.77342289686203`, 40.87892606854439`], List[4.570308744907379`, 33.26174482703209`]], List[List[60.4296378493309`, 33.26174482703209`], List[47.22652369737625`, 40.87892606854439`], List[47.22652369737625`, 56.113288551568985`], List[60.4296378493309`, 48.496107310056686`], List[60.4296378493309`, 33.26174482703209`]], List[List[59.41401368379593`, 35.03908711671829`], List[48.242147862911224`, 41.488300955295244`], List[48.242147862911224`, 54.33594626188278`], List[59.41401368379593`, 47.88673242330583`], List[59.41401368379593`, 35.03908711671829`]], List[List[19.29685914516449`, 8.125046730041504`], List[32.49997329711914`, 15.742227971553802`], List[45.70308744907379`, 8.125046730041504`], List[32.49997329711914`, 0.5078654885292053`], List[19.29685914516449`, 8.125046730041504`]], List[List[21.328107476234436`, 8.125046730041504`], List[32.49997329711914`, 14.574258631469093`], List[43.671839118003845`, 8.125046730041504`], List[32.49997329711914`, 1.6758348286139153`], List[21.328107476234436`, 8.125046730041504`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[7.109369158744812`, 32.50002670288086`], List[7.109369158744812`, 31.097747524374427`], List[5.972591313425198`, 29.960966289043427`], List[4.570308744907379`, 29.960966289043427`], List[3.168024481383867`, 29.960966289043427`], List[2.0312483310699463`, 31.097747524374427`], List[2.0312483310699463`, 32.50002670288086`], List[2.0312483310699463`, 33.90230975568602`], List[3.168024481383867`, 35.03908711671829`], List[4.570308744907379`, 35.03908711671829`], List[5.972591313425198`, 35.03908711671829`], List[7.109369158744812`, 33.90230975568602`], List[7.109369158744812`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 56.36719459295273`], List[20.82029539346695`, 54.96491250872225`], List[19.683518032434677`, 53.828134179115295`], List[18.281234979629517`, 53.828134179115295`], List[16.878951926824357`, 53.828134179115295`], List[15.742174565792084`, 54.96491250872225`], List[15.742174565792084`, 56.36719459295273`], List[15.742174565792084`, 57.76947716147055`], List[16.878951926824357`, 58.90625500679016`], List[18.281234979629517`, 58.90625500679016`], List[19.683518032434677`, 58.90625500679016`], List[20.82029539346695`, 57.76947716147055`], List[20.82029539346695`, 56.36719459295273`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 40.625020027160645`], List[20.82029539346695`, 39.222736974355485`], List[19.683518032434677`, 38.08595961332321`], List[18.281234979629517`, 38.08595961332321`], List[16.878951926824357`, 38.08595961332321`], List[15.742174565792084`, 39.222736974355485`], List[15.742174565792084`, 40.625020027160645`], List[15.742174565792084`, 42.027303079965804`], List[16.878951926824357`, 43.16408044099808`], List[18.281234979629517`, 43.16408044099808`], List[19.683518032434677`, 43.16408044099808`], List[20.82029539346695`, 42.027303079965804`], List[20.82029539346695`, 40.625020027160645`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 24.375033378601074`], List[20.82029539346695`, 22.97275420009464`], List[19.683518032434677`, 21.83597296476364`], List[18.281234979629517`, 21.83597296476364`], List[16.878951926824357`, 21.83597296476364`], List[15.742174565792084`, 22.97275420009464`], List[15.742174565792084`, 24.375033378601074`], List[15.742174565792084`, 25.777316431406234`], List[16.878951926824357`, 26.914093792438507`], List[18.281234979629517`, 26.914093792438507`], List[19.683518032434677`, 26.914093792438507`], List[20.82029539346695`, 25.777316431406234`], List[20.82029539346695`, 24.375033378601074`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 8.63285881280899`], List[20.82029539346695`, 7.230591257198739`], List[19.683518032434677`, 6.093798398971558`], List[18.281234979629517`, 6.093798398971558`], List[16.878951926824357`, 6.093798398971558`], List[15.742174565792084`, 7.230591257198739`], List[15.742174565792084`, 8.63285881280899`], List[15.742174565792084`, 10.035130242717969`], List[16.878951926824357`, 11.171919226646423`], List[18.281234979629517`, 11.171919226646423`], List[19.683518032434677`, 11.171919226646423`], List[20.82029539346695`, 10.035130242717969`], List[20.82029539346695`, 8.63285881280899`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 48.75001335144043`], List[35.03903371095657`, 47.34773029863527`], List[33.90225247562557`, 46.210952937603`], List[32.49997329711914`, 46.210952937603`], List[31.09769024431398`, 46.210952937603`], List[29.960912883281708`, 47.34773029863527`], List[29.960912883281708`, 48.75001335144043`], List[29.960912883281708`, 50.15229543567091`], List[31.09769024431398`, 51.28907376527786`], List[32.49997329711914`, 51.28907376527786`], List[33.90225247562557`, 51.28907376527786`], List[35.03903371095657`, 50.15229543567091`], List[35.03903371095657`, 48.75001335144043`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 32.50002670288086`], List[35.03903371095657`, 31.097747524374427`], List[33.90225247562557`, 29.960966289043427`], List[32.49997329711914`, 29.960966289043427`], List[31.09769024431398`, 29.960966289043427`], List[29.960912883281708`, 31.097747524374427`], List[29.960912883281708`, 32.50002670288086`], List[29.960912883281708`, 33.90230975568602`], List[31.09769024431398`, 35.03908711671829`], List[32.49997329711914`, 35.03908711671829`], List[33.90225247562557`, 35.03908711671829`], List[35.03903371095657`, 33.90230975568602`], List[35.03903371095657`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 16.25004005432129`], List[35.03903371095657`, 14.847760875814856`], List[33.90225247562557`, 13.710979640483856`], List[32.49997329711914`, 13.710979640483856`], List[31.09769024431398`, 13.710979640483856`], List[29.960912883281708`, 14.847760875814856`], List[29.960912883281708`, 16.25004005432129`], List[29.960912883281708`, 17.65232310712645`], List[31.09769024431398`, 18.789100468158722`], List[32.49997329711914`, 18.789100468158722`], List[33.90225247562557`, 18.789100468158722`], List[35.03903371095657`, 17.65232310712645`], List[35.03903371095657`, 16.25004005432129`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 56.36719459295273`], List[49.2577720284462`, 54.96491250872225`], List[48.1209907931152`, 53.828134179115295`], List[46.718711614608765`, 53.828134179115295`], List[45.316428561803605`, 53.828134179115295`], List[44.17965120077133`, 54.96491250872225`], List[44.17965120077133`, 56.36719459295273`], List[44.17965120077133`, 57.76947716147055`], List[45.316428561803605`, 58.90625500679016`], List[46.718711614608765`, 58.90625500679016`], List[48.1209907931152`, 58.90625500679016`], List[49.2577720284462`, 57.76947716147055`], List[49.2577720284462`, 56.36719459295273`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 40.625020027160645`], List[49.2577720284462`, 39.222736974355485`], List[48.1209907931152`, 38.08595961332321`], List[46.718711614608765`, 38.08595961332321`], List[45.316428561803605`, 38.08595961332321`], List[44.17965120077133`, 39.222736974355485`], List[44.17965120077133`, 40.625020027160645`], List[44.17965120077133`, 42.027303079965804`], List[45.316428561803605`, 43.16408044099808`], List[46.718711614608765`, 43.16408044099808`], List[48.1209907931152`, 43.16408044099808`], List[49.2577720284462`, 42.027303079965804`], List[49.2577720284462`, 40.625020027160645`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 24.375033378601074`], List[49.2577720284462`, 22.97275420009464`], List[48.1209907931152`, 21.83597296476364`], List[46.718711614608765`, 21.83597296476364`], List[45.316428561803605`, 21.83597296476364`], List[44.17965120077133`, 22.97275420009464`], List[44.17965120077133`, 24.375033378601074`], List[44.17965120077133`, 25.777316431406234`], List[45.316428561803605`, 26.914093792438507`], List[46.718711614608765`, 26.914093792438507`], List[48.1209907931152`, 26.914093792438507`], List[49.2577720284462`, 25.777316431406234`], List[49.2577720284462`, 24.375033378601074`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 8.63285881280899`], List[49.2577720284462`, 7.230591257198739`], List[48.1209907931152`, 6.093798398971558`], List[46.718711614608765`, 6.093798398971558`], List[45.316428561803605`, 6.093798398971558`], List[44.17965120077133`, 7.230591257198739`], List[44.17965120077133`, 8.63285881280899`], List[44.17965120077133`, 10.035130242717969`], List[45.316428561803605`, 11.171919226646423`], List[46.718711614608765`, 11.171919226646423`], List[48.1209907931152`, 11.171919226646423`], List[49.2577720284462`, 10.035130242717969`], List[49.2577720284462`, 8.63285881280899`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[62.968698263168335`, 32.50002670288086`], List[62.968698263168335`, 31.097747524374427`], List[61.83190540494115`, 29.960966289043427`], List[60.4296378493309`, 29.960966289043427`], List[59.027366419421924`, 29.960966289043427`], List[57.89057743549347`, 31.097747524374427`], List[57.89057743549347`, 32.50002670288086`], List[57.89057743549347`, 33.90230975568602`], List[59.027366419421924`, 35.03908711671829`], List[60.4296378493309`, 35.03908711671829`], List[61.83190540494115`, 35.03908711671829`], List[62.968698263168335`, 33.90230975568602`], List[62.968698263168335`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]]], List[Rule[BaselinePosition, Scaled[0.15`]], Rule[ImageSize, 10], Rule[ImageSize, List[Automatic, 35]]]], StyleBox[RowBox[List["QuantumDistance", " "]], Rule[ShowAutoStyles, False], Rule[ShowStringCharacters, False], Rule[FontSize, Times[0.9`, Inherited]], Rule[FontColor, GrayLevel[0.1`]]]]], Rule[GridBoxSpacings, List[Rule["Columns", List[List[0.25`]]]]]], Rule[Alignment, List[Left, Baseline]], Rule[BaselinePosition, Baseline], Rule[FrameMargins, List[List[3, 0], List[0, 0]]], Rule[BaseStyle, List[Rule[LineSpacing, List[0, 0]], Rule[LineBreakWithin, False]]]], RowBox[List["PacletSymbol", "[", RowBox[List["\"Wolfram/QuantumFramework\"", ",", "\"QuantumDistance\""]], "]"]], Rule[TooltipStyle, List[Rule[ShowAutoStyles, True], Rule[ShowStringCharacters, True]]]], Function[Annotation[Slot[1], Style[Defer[PacletSymbol["Wolfram/QuantumFramework", "QuantumDistance"]], Rule[ShowStringCharacters, True]], "Tooltip"]]], Rule[Background, RGBColor[0.968`, 0.976`, 0.984`]], Rule[BaselinePosition, Baseline], Rule[DefaultBaseStyle, List[]], Rule[FrameMargins, List[List[0, 0], List[1, 1]]], Rule[FrameStyle, RGBColor[0.831`, 0.847`, 0.85`]], Rule[RoundingRadius, 4]], PacletSymbol["Wolfram/QuantumFramework", "QuantumDistance"], Rule[Selectable, False], Rule[SelectWithContents, True], Rule[BoxID, "PacletSymbolBox"]][\[Psi]1, \[Psi]2, #] &, {"Fidelity", "Trace", "BuresAngle", "HilbertSchmidt"}]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/61efa41e82b239c3.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/7fafe470-0d0a-4108-afcb-f604aad997d0"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/56db5ac0f33417ba.png)
![qc["Diagram", "WireLabels" -> {{Placed["\!\(\*SubscriptBox[\(a\), \(i\)]\)", Left],
Placed["\!\(\*SubscriptBox[\(a\), \(f\)]\)", Right]}, {Placed[
"\!\(\*SubscriptBox[\(b\), \(i\)]\)", Left], Placed["\!\(\*SubscriptBox[\(b\), \(f\)]\)", Right]}}, "MeasurementWireLabel" -> "M"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/2544f3f4838edc0a.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/1955c813-fca1-4eaf-bf3b-41b192c215c0"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/1744ed6fd8444e5e.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/fa9a8b7f-81a9-4d7e-a6bd-7394f72e5ef2"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/522a5e7f203c9d31.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/444ac1a6-888d-4744-a17d-7a5e0ac9b35c"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/6710ab79ee699075.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/c8277eb5-8617-495a-83fb-9713e7445521"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/73b511aade9c0d33.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/dc3923d3-7050-495d-b6ff-bb90ee0259ff"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/61afc412ca6019d5.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/8be38932-d470-43f8-bd7a-0732568c980d"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/1a1f4b835282650f.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/aa11846a-c740-487a-bace-7f570d6394e6"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/6804dfb229d903b4.png)
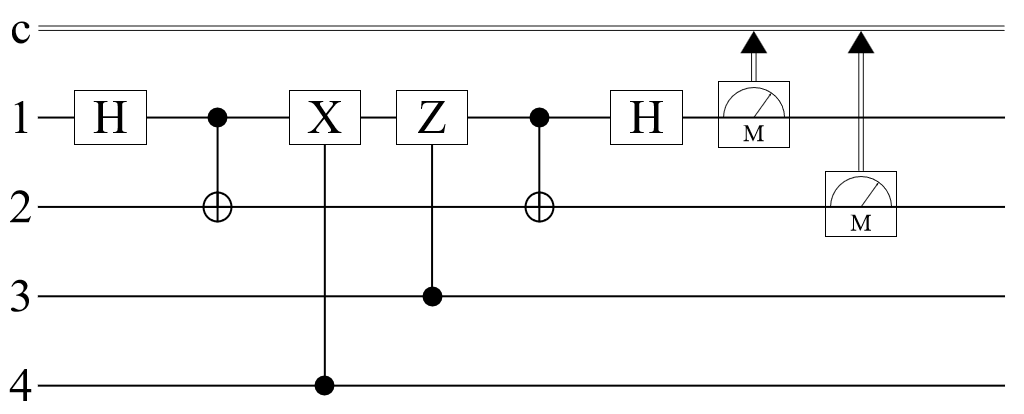
![superdense[InterpretationBox[FrameBox[TagBox[TooltipBox[PaneBox[GridBox[List[List[GraphicsBox[List[Thickness[0.015384615384615385`], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[19.29685914516449`, 56.875006675720215`], List[32.49997329711914`, 64.49218791723251`], List[45.70308744907379`, 56.875006675720215`], List[32.49997329711914`, 49.257825434207916`], List[19.29685914516449`, 56.875006675720215`]], List[List[21.328107476234436`, 56.875006675720215`], List[32.49997329711914`, 63.32422015108166`], List[43.671839118003845`, 56.875006675720215`], List[32.49997329711914`, 50.42579283714326`], List[21.328107476234436`, 56.875006675720215`]], List[List[33.00778537988663`, 33.26174482703209`], List[33.00778537988663`, 48.496107310056686`], List[46.21089953184128`, 56.113288551568985`], List[46.21089953184128`, 40.87892606854439`], List[33.00778537988663`, 33.26174482703209`]]]]], List[FaceForm[RGBColor[0.7019607843137254`, 0.6039215686274509`, 0.788235294117647`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[31.992161214351654`, 33.26174482703209`], List[18.789047062397003`, 40.87892606854439`], List[18.789047062397003`, 56.113288551568985`], List[31.992161214351654`, 48.496107310056686`], List[31.992161214351654`, 33.26174482703209`]]]]], List[FaceForm[RGBColor[0.5372549019607843`, 0.403921568627451`, 0.6745098039215687`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[17.77342289686203`, 8.886764854192734`], List[4.570308744907379`, 16.503946095705032`], List[4.570308744907379`, 31.73830857872963`], List[17.77342289686203`, 24.12112733721733`], List[17.77342289686203`, 8.886764854192734`]], List[List[16.757798731327057`, 10.664107143878937`], List[5.585932910442352`, 17.113319045306525`], List[5.585932910442352`, 29.960966289043427`], List[16.757798731327057`, 23.511754387615838`], List[16.757798731327057`, 10.664107143878937`]], List[List[31.484349131584167`, 32.50002670288086`], List[18.281234979629517`, 40.11720794439316`], List[5.078120827674866`, 32.50002670288086`], List[18.281234979629517`, 24.88284546136856`], List[31.484349131584167`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.6352941176470588`, 0.7333333333333333`, 0.8313725490196079`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[31.992161214351654`, 31.73830857872963`], List[18.789047062397003`, 24.12112733721733`], List[18.789047062397003`, 8.886764854192734`], List[31.992161214351654`, 16.503946095705032`], List[31.992161214351654`, 31.73830857872963`]]]]], List[FaceForm[RGBColor[0.2901960784313726`, 0.40784313725490196`, 0.5764705882352941`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[47.22652369737625`, 8.886764854192734`], List[47.22652369737625`, 24.12112733721733`], List[60.4296378493309`, 31.73830857872963`], List[60.4296378493309`, 16.503946095705032`], List[47.22652369737625`, 8.886764854192734`]], List[List[48.242147862911224`, 10.664107143878937`], List[48.242147862911224`, 23.511754387615838`], List[59.41401368379593`, 29.960966289043427`], List[59.41401368379593`, 17.113319045306525`], List[48.242147862911224`, 10.664107143878937`]], List[List[33.515597462654114`, 32.50002670288086`], List[46.718711614608765`, 40.11720794439316`], List[59.921825766563416`, 32.50002670288086`], List[46.718711614608765`, 24.88284546136856`], List[33.515597462654114`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.6`, 0.6`, 0.37254901960784315`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[33.00778537988663`, 31.73830857872963`], List[33.00778537988663`, 16.503946095705032`], List[46.21089953184128`, 8.886764854192734`], List[46.21089953184128`, 24.12112733721733`], List[33.00778537988663`, 31.73830857872963`]]]]], List[FaceForm[RGBColor[0.396078431372549`, 0.6039215686274509`, 0.30196078431372547`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[5.585932910442352`, 35.03908711671829`], List[5.585932910442352`, 47.88673242330583`], List[16.757798731327057`, 54.33594626188278`], List[16.757798731327057`, 41.488300955295244`], List[5.585932910442352`, 35.03908711671829`]], List[List[4.570308744907379`, 33.26174482703209`], List[4.570308744907379`, 48.496107310056686`], List[17.77342289686203`, 56.113288551568985`], List[17.77342289686203`, 40.87892606854439`], List[4.570308744907379`, 33.26174482703209`]], List[List[60.4296378493309`, 33.26174482703209`], List[47.22652369737625`, 40.87892606854439`], List[47.22652369737625`, 56.113288551568985`], List[60.4296378493309`, 48.496107310056686`], List[60.4296378493309`, 33.26174482703209`]], List[List[59.41401368379593`, 35.03908711671829`], List[48.242147862911224`, 41.488300955295244`], List[48.242147862911224`, 54.33594626188278`], List[59.41401368379593`, 47.88673242330583`], List[59.41401368379593`, 35.03908711671829`]], List[List[19.29685914516449`, 8.125046730041504`], List[32.49997329711914`, 15.742227971553802`], List[45.70308744907379`, 8.125046730041504`], List[32.49997329711914`, 0.5078654885292053`], List[19.29685914516449`, 8.125046730041504`]], List[List[21.328107476234436`, 8.125046730041504`], List[32.49997329711914`, 14.574258631469093`], List[43.671839118003845`, 8.125046730041504`], List[32.49997329711914`, 1.6758348286139153`], List[21.328107476234436`, 8.125046730041504`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[7.109369158744812`, 32.50002670288086`], List[7.109369158744812`, 31.097747524374427`], List[5.972591313425198`, 29.960966289043427`], List[4.570308744907379`, 29.960966289043427`], List[3.168024481383867`, 29.960966289043427`], List[2.0312483310699463`, 31.097747524374427`], List[2.0312483310699463`, 32.50002670288086`], List[2.0312483310699463`, 33.90230975568602`], List[3.168024481383867`, 35.03908711671829`], List[4.570308744907379`, 35.03908711671829`], List[5.972591313425198`, 35.03908711671829`], List[7.109369158744812`, 33.90230975568602`], List[7.109369158744812`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 56.36719459295273`], List[20.82029539346695`, 54.96491250872225`], List[19.683518032434677`, 53.828134179115295`], List[18.281234979629517`, 53.828134179115295`], List[16.878951926824357`, 53.828134179115295`], List[15.742174565792084`, 54.96491250872225`], List[15.742174565792084`, 56.36719459295273`], List[15.742174565792084`, 57.76947716147055`], List[16.878951926824357`, 58.90625500679016`], List[18.281234979629517`, 58.90625500679016`], List[19.683518032434677`, 58.90625500679016`], List[20.82029539346695`, 57.76947716147055`], List[20.82029539346695`, 56.36719459295273`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 40.625020027160645`], List[20.82029539346695`, 39.222736974355485`], List[19.683518032434677`, 38.08595961332321`], List[18.281234979629517`, 38.08595961332321`], List[16.878951926824357`, 38.08595961332321`], List[15.742174565792084`, 39.222736974355485`], List[15.742174565792084`, 40.625020027160645`], List[15.742174565792084`, 42.027303079965804`], List[16.878951926824357`, 43.16408044099808`], List[18.281234979629517`, 43.16408044099808`], List[19.683518032434677`, 43.16408044099808`], List[20.82029539346695`, 42.027303079965804`], List[20.82029539346695`, 40.625020027160645`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 24.375033378601074`], List[20.82029539346695`, 22.97275420009464`], List[19.683518032434677`, 21.83597296476364`], List[18.281234979629517`, 21.83597296476364`], List[16.878951926824357`, 21.83597296476364`], List[15.742174565792084`, 22.97275420009464`], List[15.742174565792084`, 24.375033378601074`], List[15.742174565792084`, 25.777316431406234`], List[16.878951926824357`, 26.914093792438507`], List[18.281234979629517`, 26.914093792438507`], List[19.683518032434677`, 26.914093792438507`], List[20.82029539346695`, 25.777316431406234`], List[20.82029539346695`, 24.375033378601074`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 8.63285881280899`], List[20.82029539346695`, 7.230591257198739`], List[19.683518032434677`, 6.093798398971558`], List[18.281234979629517`, 6.093798398971558`], List[16.878951926824357`, 6.093798398971558`], List[15.742174565792084`, 7.230591257198739`], List[15.742174565792084`, 8.63285881280899`], List[15.742174565792084`, 10.035130242717969`], List[16.878951926824357`, 11.171919226646423`], List[18.281234979629517`, 11.171919226646423`], List[19.683518032434677`, 11.171919226646423`], List[20.82029539346695`, 10.035130242717969`], List[20.82029539346695`, 8.63285881280899`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 48.75001335144043`], List[35.03903371095657`, 47.34773029863527`], List[33.90225247562557`, 46.210952937603`], List[32.49997329711914`, 46.210952937603`], List[31.09769024431398`, 46.210952937603`], List[29.960912883281708`, 47.34773029863527`], List[29.960912883281708`, 48.75001335144043`], List[29.960912883281708`, 50.15229543567091`], List[31.09769024431398`, 51.28907376527786`], List[32.49997329711914`, 51.28907376527786`], List[33.90225247562557`, 51.28907376527786`], List[35.03903371095657`, 50.15229543567091`], List[35.03903371095657`, 48.75001335144043`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 32.50002670288086`], List[35.03903371095657`, 31.097747524374427`], List[33.90225247562557`, 29.960966289043427`], List[32.49997329711914`, 29.960966289043427`], List[31.09769024431398`, 29.960966289043427`], List[29.960912883281708`, 31.097747524374427`], List[29.960912883281708`, 32.50002670288086`], List[29.960912883281708`, 33.90230975568602`], List[31.09769024431398`, 35.03908711671829`], List[32.49997329711914`, 35.03908711671829`], List[33.90225247562557`, 35.03908711671829`], List[35.03903371095657`, 33.90230975568602`], List[35.03903371095657`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 16.25004005432129`], List[35.03903371095657`, 14.847760875814856`], List[33.90225247562557`, 13.710979640483856`], List[32.49997329711914`, 13.710979640483856`], List[31.09769024431398`, 13.710979640483856`], List[29.960912883281708`, 14.847760875814856`], List[29.960912883281708`, 16.25004005432129`], List[29.960912883281708`, 17.65232310712645`], List[31.09769024431398`, 18.789100468158722`], List[32.49997329711914`, 18.789100468158722`], List[33.90225247562557`, 18.789100468158722`], List[35.03903371095657`, 17.65232310712645`], List[35.03903371095657`, 16.25004005432129`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 56.36719459295273`], List[49.2577720284462`, 54.96491250872225`], List[48.1209907931152`, 53.828134179115295`], List[46.718711614608765`, 53.828134179115295`], List[45.316428561803605`, 53.828134179115295`], List[44.17965120077133`, 54.96491250872225`], List[44.17965120077133`, 56.36719459295273`], List[44.17965120077133`, 57.76947716147055`], List[45.316428561803605`, 58.90625500679016`], List[46.718711614608765`, 58.90625500679016`], List[48.1209907931152`, 58.90625500679016`], List[49.2577720284462`, 57.76947716147055`], List[49.2577720284462`, 56.36719459295273`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 40.625020027160645`], List[49.2577720284462`, 39.222736974355485`], List[48.1209907931152`, 38.08595961332321`], List[46.718711614608765`, 38.08595961332321`], List[45.316428561803605`, 38.08595961332321`], List[44.17965120077133`, 39.222736974355485`], List[44.17965120077133`, 40.625020027160645`], List[44.17965120077133`, 42.027303079965804`], List[45.316428561803605`, 43.16408044099808`], List[46.718711614608765`, 43.16408044099808`], List[48.1209907931152`, 43.16408044099808`], List[49.2577720284462`, 42.027303079965804`], List[49.2577720284462`, 40.625020027160645`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 24.375033378601074`], List[49.2577720284462`, 22.97275420009464`], List[48.1209907931152`, 21.83597296476364`], List[46.718711614608765`, 21.83597296476364`], List[45.316428561803605`, 21.83597296476364`], List[44.17965120077133`, 22.97275420009464`], List[44.17965120077133`, 24.375033378601074`], List[44.17965120077133`, 25.777316431406234`], List[45.316428561803605`, 26.914093792438507`], List[46.718711614608765`, 26.914093792438507`], List[48.1209907931152`, 26.914093792438507`], List[49.2577720284462`, 25.777316431406234`], List[49.2577720284462`, 24.375033378601074`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 8.63285881280899`], List[49.2577720284462`, 7.230591257198739`], List[48.1209907931152`, 6.093798398971558`], List[46.718711614608765`, 6.093798398971558`], List[45.316428561803605`, 6.093798398971558`], List[44.17965120077133`, 7.230591257198739`], List[44.17965120077133`, 8.63285881280899`], List[44.17965120077133`, 10.035130242717969`], List[45.316428561803605`, 11.171919226646423`], List[46.718711614608765`, 11.171919226646423`], List[48.1209907931152`, 11.171919226646423`], List[49.2577720284462`, 10.035130242717969`], List[49.2577720284462`, 8.63285881280899`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[62.968698263168335`, 32.50002670288086`], List[62.968698263168335`, 31.097747524374427`], List[61.83190540494115`, 29.960966289043427`], List[60.4296378493309`, 29.960966289043427`], List[59.027366419421924`, 29.960966289043427`], List[57.89057743549347`, 31.097747524374427`], List[57.89057743549347`, 32.50002670288086`], List[57.89057743549347`, 33.90230975568602`], List[59.027366419421924`, 35.03908711671829`], List[60.4296378493309`, 35.03908711671829`], List[61.83190540494115`, 35.03908711671829`], List[62.968698263168335`, 33.90230975568602`], List[62.968698263168335`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]]], List[Rule[BaselinePosition, Scaled[0.15`]], Rule[ImageSize, 10], Rule[ImageSize, List[Automatic, 35]]]], StyleBox[RowBox[List["QuantumState", " "]], Rule[ShowAutoStyles, False], Rule[ShowStringCharacters, False], Rule[FontSize, Times[0.9`, Inherited]], Rule[FontColor, GrayLevel[0.1`]]]]], Rule[GridBoxSpacings, List[Rule["Columns", List[List[0.25`]]]]]], Rule[Alignment, List[Left, Baseline]], Rule[BaselinePosition, Baseline], Rule[FrameMargins, List[List[3, 0], List[0, 0]]], Rule[BaseStyle, List[Rule[LineSpacing, List[0, 0]], Rule[LineBreakWithin, False]]]], RowBox[List["PacletSymbol", "[", RowBox[List["\"Wolfram/QuantumFramework\"", ",", "\"QuantumState\""]], "]"]], Rule[TooltipStyle, List[Rule[ShowAutoStyles, True], Rule[ShowStringCharacters, True]]]], Function[Annotation[Slot[1], Style[Defer[PacletSymbol["Wolfram/QuantumFramework", "QuantumState"]], Rule[ShowStringCharacters, True]], "Tooltip"]]], Rule[Background, RGBColor[0.968`, 0.976`, 0.984`]], Rule[BaselinePosition, Baseline], Rule[DefaultBaseStyle, List[]], Rule[FrameMargins, List[List[0, 0], List[1, 1]]], Rule[FrameStyle, RGBColor[0.831`, 0.847`, 0.85`]], Rule[RoundingRadius, 4]], PacletSymbol["Wolfram/QuantumFramework", "QuantumState"], Rule[Selectable, False], Rule[SelectWithContents, True], Rule[BoxID, "PacletSymbolBox"]][
"00" <> #1 <> #2]]["ProbabilityPlot"] & @@@ Tuples[{"0", "1"}, 2] // Row](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/26836cd9b137a9ac.png)
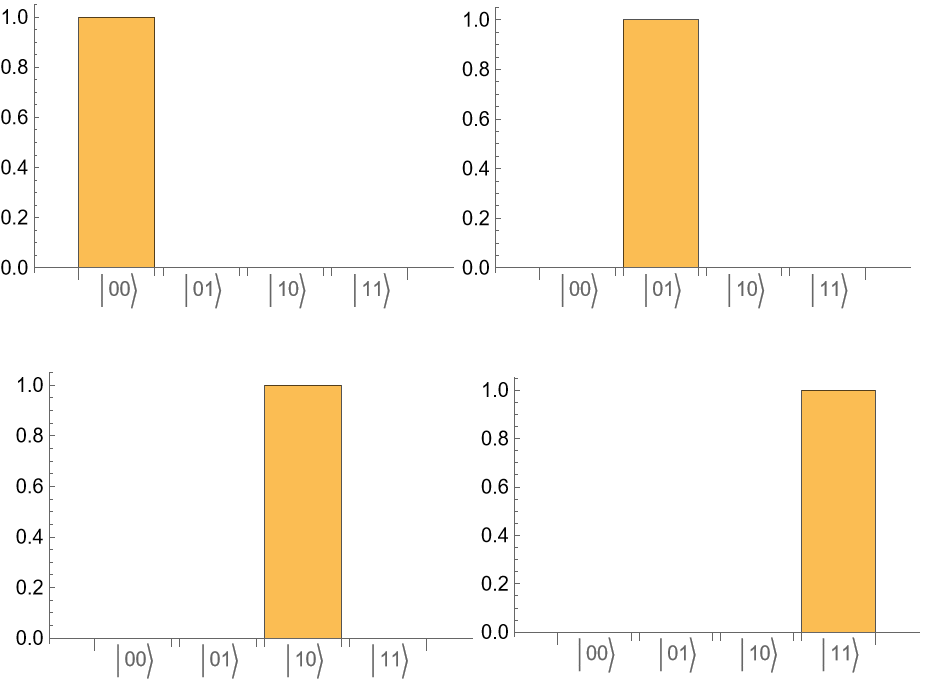
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/93b6cf3d-fcb7-4128-a4c1-68b2562bc9ce"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/12684353c4fb0459.png)
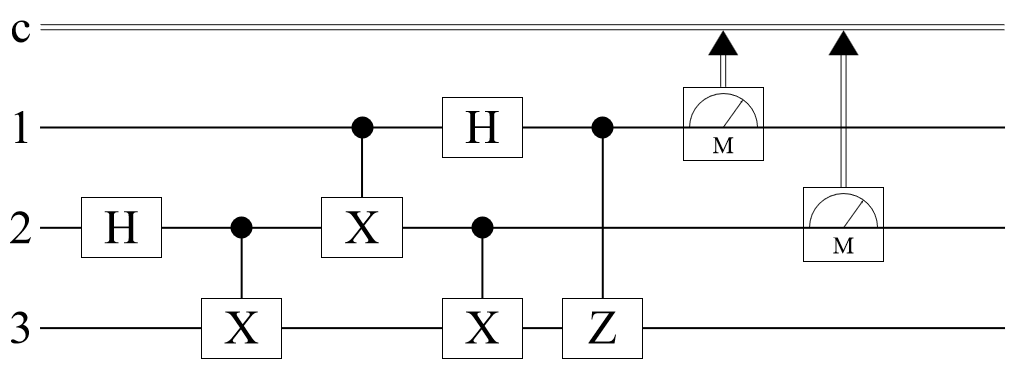
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/2a2ec12d-2645-409d-8fa4-8e827ec1b892"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/66e06062c922b7ec.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/deb98b63-132b-4ce1-a1cd-f1df41579a0d"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/7624e65eccae7e87.png)
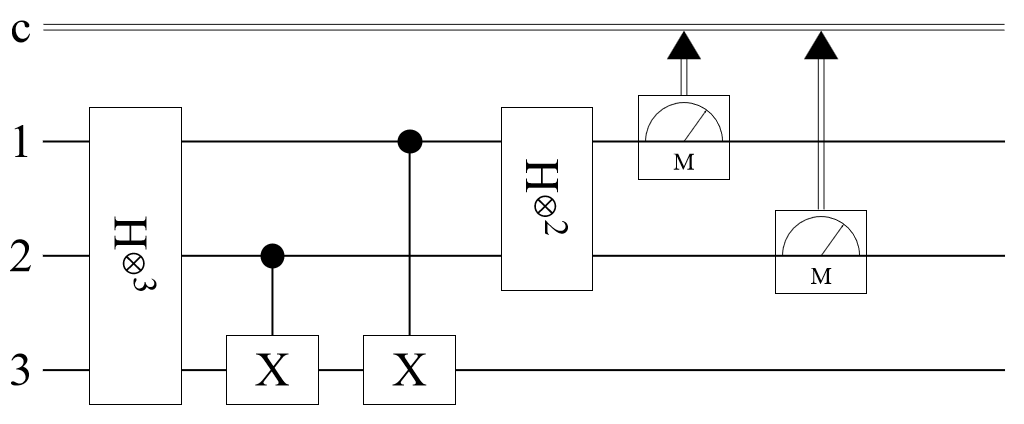
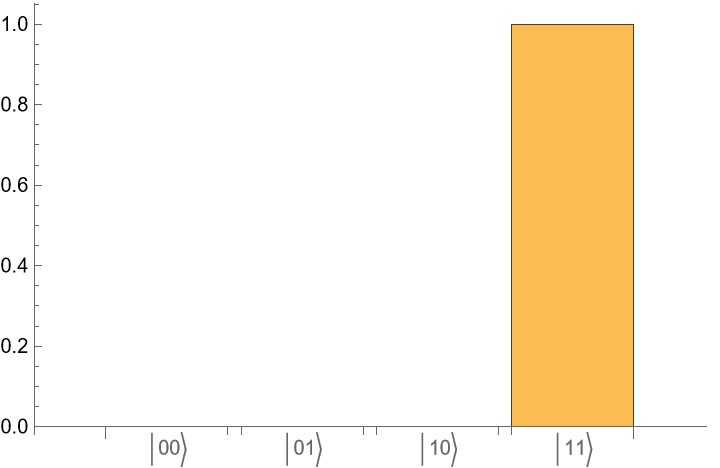
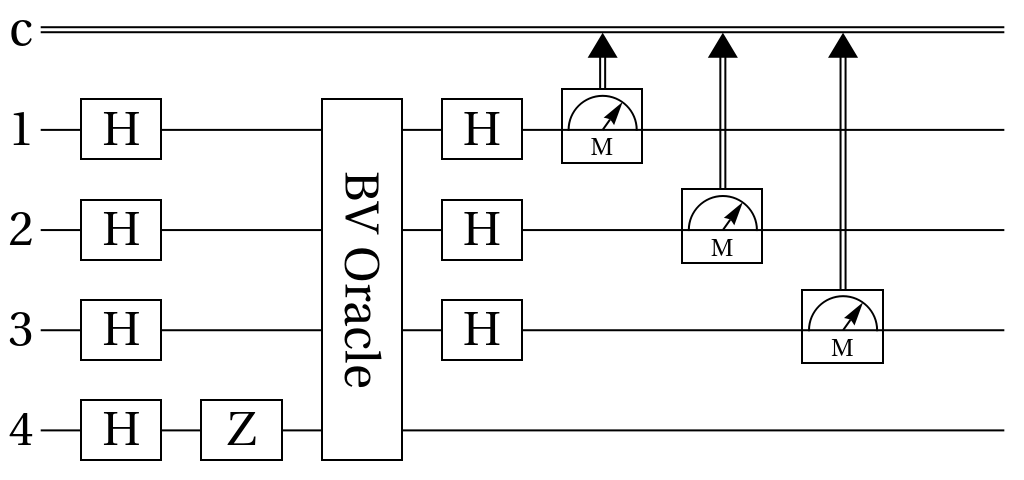
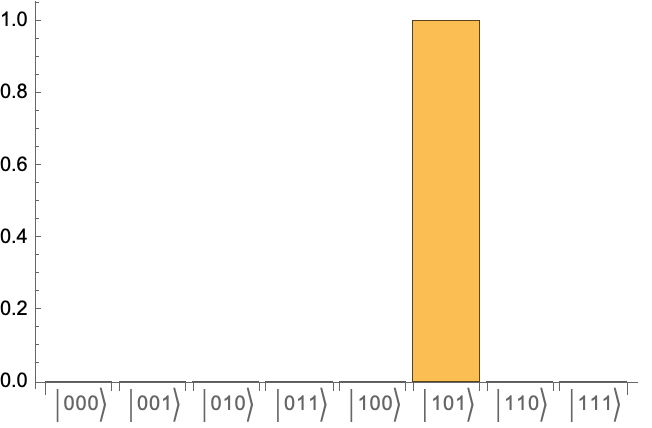

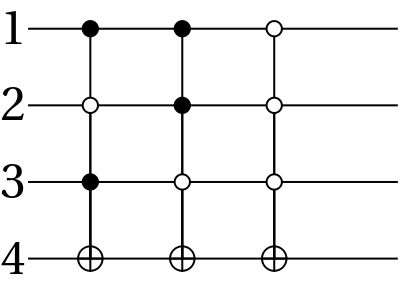
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/5a900593-73ac-4fc7-9be1-8db8a9c7e02c"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/499b89221a742827.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/30f09088-5b39-4e83-98c4-fb25ba6ef926"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/2824a84058cfca47.png)

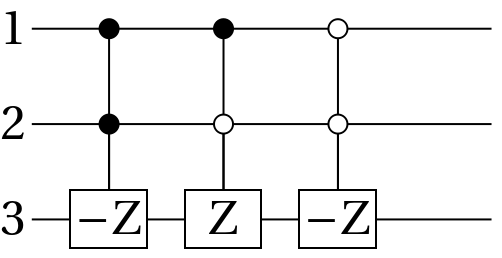
![Module[{index = Table[InterpretationBox[FrameBox[TagBox[TooltipBox[PaneBox[GridBox[List[List[GraphicsBox[List[Thickness[0.015384615384615385`], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[19.29685914516449`, 56.875006675720215`], List[32.49997329711914`, 64.49218791723251`], List[45.70308744907379`, 56.875006675720215`], List[32.49997329711914`, 49.257825434207916`], List[19.29685914516449`, 56.875006675720215`]], List[List[21.328107476234436`, 56.875006675720215`], List[32.49997329711914`, 63.32422015108166`], List[43.671839118003845`, 56.875006675720215`], List[32.49997329711914`, 50.42579283714326`], List[21.328107476234436`, 56.875006675720215`]], List[List[33.00778537988663`, 33.26174482703209`], List[33.00778537988663`, 48.496107310056686`], List[46.21089953184128`, 56.113288551568985`], List[46.21089953184128`, 40.87892606854439`], List[33.00778537988663`, 33.26174482703209`]]]]], List[FaceForm[RGBColor[0.7019607843137254`, 0.6039215686274509`, 0.788235294117647`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[31.992161214351654`, 33.26174482703209`], List[18.789047062397003`, 40.87892606854439`], List[18.789047062397003`, 56.113288551568985`], List[31.992161214351654`, 48.496107310056686`], List[31.992161214351654`, 33.26174482703209`]]]]], List[FaceForm[RGBColor[0.5372549019607843`, 0.403921568627451`, 0.6745098039215687`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[17.77342289686203`, 8.886764854192734`], List[4.570308744907379`, 16.503946095705032`], List[4.570308744907379`, 31.73830857872963`], List[17.77342289686203`, 24.12112733721733`], List[17.77342289686203`, 8.886764854192734`]], List[List[16.757798731327057`, 10.664107143878937`], List[5.585932910442352`, 17.113319045306525`], List[5.585932910442352`, 29.960966289043427`], List[16.757798731327057`, 23.511754387615838`], List[16.757798731327057`, 10.664107143878937`]], List[List[31.484349131584167`, 32.50002670288086`], List[18.281234979629517`, 40.11720794439316`], List[5.078120827674866`, 32.50002670288086`], List[18.281234979629517`, 24.88284546136856`], List[31.484349131584167`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.6352941176470588`, 0.7333333333333333`, 0.8313725490196079`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[31.992161214351654`, 31.73830857872963`], List[18.789047062397003`, 24.12112733721733`], List[18.789047062397003`, 8.886764854192734`], List[31.992161214351654`, 16.503946095705032`], List[31.992161214351654`, 31.73830857872963`]]]]], List[FaceForm[RGBColor[0.2901960784313726`, 0.40784313725490196`, 0.5764705882352941`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[47.22652369737625`, 8.886764854192734`], List[47.22652369737625`, 24.12112733721733`], List[60.4296378493309`, 31.73830857872963`], List[60.4296378493309`, 16.503946095705032`], List[47.22652369737625`, 8.886764854192734`]], List[List[48.242147862911224`, 10.664107143878937`], List[48.242147862911224`, 23.511754387615838`], List[59.41401368379593`, 29.960966289043427`], List[59.41401368379593`, 17.113319045306525`], List[48.242147862911224`, 10.664107143878937`]], List[List[33.515597462654114`, 32.50002670288086`], List[46.718711614608765`, 40.11720794439316`], List[59.921825766563416`, 32.50002670288086`], List[46.718711614608765`, 24.88284546136856`], List[33.515597462654114`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.6`, 0.6`, 0.37254901960784315`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[33.00778537988663`, 31.73830857872963`], List[33.00778537988663`, 16.503946095705032`], List[46.21089953184128`, 8.886764854192734`], List[46.21089953184128`, 24.12112733721733`], List[33.00778537988663`, 31.73830857872963`]]]]], List[FaceForm[RGBColor[0.396078431372549`, 0.6039215686274509`, 0.30196078431372547`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[5.585932910442352`, 35.03908711671829`], List[5.585932910442352`, 47.88673242330583`], List[16.757798731327057`, 54.33594626188278`], List[16.757798731327057`, 41.488300955295244`], List[5.585932910442352`, 35.03908711671829`]], List[List[4.570308744907379`, 33.26174482703209`], List[4.570308744907379`, 48.496107310056686`], List[17.77342289686203`, 56.113288551568985`], List[17.77342289686203`, 40.87892606854439`], List[4.570308744907379`, 33.26174482703209`]], List[List[60.4296378493309`, 33.26174482703209`], List[47.22652369737625`, 40.87892606854439`], List[47.22652369737625`, 56.113288551568985`], List[60.4296378493309`, 48.496107310056686`], List[60.4296378493309`, 33.26174482703209`]], List[List[59.41401368379593`, 35.03908711671829`], List[48.242147862911224`, 41.488300955295244`], List[48.242147862911224`, 54.33594626188278`], List[59.41401368379593`, 47.88673242330583`], List[59.41401368379593`, 35.03908711671829`]], List[List[19.29685914516449`, 8.125046730041504`], List[32.49997329711914`, 15.742227971553802`], List[45.70308744907379`, 8.125046730041504`], List[32.49997329711914`, 0.5078654885292053`], List[19.29685914516449`, 8.125046730041504`]], List[List[21.328107476234436`, 8.125046730041504`], List[32.49997329711914`, 14.574258631469093`], List[43.671839118003845`, 8.125046730041504`], List[32.49997329711914`, 1.6758348286139153`], List[21.328107476234436`, 8.125046730041504`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[7.109369158744812`, 32.50002670288086`], List[7.109369158744812`, 31.097747524374427`], List[5.972591313425198`, 29.960966289043427`], List[4.570308744907379`, 29.960966289043427`], List[3.168024481383867`, 29.960966289043427`], List[2.0312483310699463`, 31.097747524374427`], List[2.0312483310699463`, 32.50002670288086`], List[2.0312483310699463`, 33.90230975568602`], List[3.168024481383867`, 35.03908711671829`], List[4.570308744907379`, 35.03908711671829`], List[5.972591313425198`, 35.03908711671829`], List[7.109369158744812`, 33.90230975568602`], List[7.109369158744812`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 56.36719459295273`], List[20.82029539346695`, 54.96491250872225`], List[19.683518032434677`, 53.828134179115295`], List[18.281234979629517`, 53.828134179115295`], List[16.878951926824357`, 53.828134179115295`], List[15.742174565792084`, 54.96491250872225`], List[15.742174565792084`, 56.36719459295273`], List[15.742174565792084`, 57.76947716147055`], List[16.878951926824357`, 58.90625500679016`], List[18.281234979629517`, 58.90625500679016`], List[19.683518032434677`, 58.90625500679016`], List[20.82029539346695`, 57.76947716147055`], List[20.82029539346695`, 56.36719459295273`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 40.625020027160645`], List[20.82029539346695`, 39.222736974355485`], List[19.683518032434677`, 38.08595961332321`], List[18.281234979629517`, 38.08595961332321`], List[16.878951926824357`, 38.08595961332321`], List[15.742174565792084`, 39.222736974355485`], List[15.742174565792084`, 40.625020027160645`], List[15.742174565792084`, 42.027303079965804`], List[16.878951926824357`, 43.16408044099808`], List[18.281234979629517`, 43.16408044099808`], List[19.683518032434677`, 43.16408044099808`], List[20.82029539346695`, 42.027303079965804`], List[20.82029539346695`, 40.625020027160645`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 24.375033378601074`], List[20.82029539346695`, 22.97275420009464`], List[19.683518032434677`, 21.83597296476364`], List[18.281234979629517`, 21.83597296476364`], List[16.878951926824357`, 21.83597296476364`], List[15.742174565792084`, 22.97275420009464`], List[15.742174565792084`, 24.375033378601074`], List[15.742174565792084`, 25.777316431406234`], List[16.878951926824357`, 26.914093792438507`], List[18.281234979629517`, 26.914093792438507`], List[19.683518032434677`, 26.914093792438507`], List[20.82029539346695`, 25.777316431406234`], List[20.82029539346695`, 24.375033378601074`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 8.63285881280899`], List[20.82029539346695`, 7.230591257198739`], List[19.683518032434677`, 6.093798398971558`], List[18.281234979629517`, 6.093798398971558`], List[16.878951926824357`, 6.093798398971558`], List[15.742174565792084`, 7.230591257198739`], List[15.742174565792084`, 8.63285881280899`], List[15.742174565792084`, 10.035130242717969`], List[16.878951926824357`, 11.171919226646423`], List[18.281234979629517`, 11.171919226646423`], List[19.683518032434677`, 11.171919226646423`], List[20.82029539346695`, 10.035130242717969`], List[20.82029539346695`, 8.63285881280899`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 48.75001335144043`], List[35.03903371095657`, 47.34773029863527`], List[33.90225247562557`, 46.210952937603`], List[32.49997329711914`, 46.210952937603`], List[31.09769024431398`, 46.210952937603`], List[29.960912883281708`, 47.34773029863527`], List[29.960912883281708`, 48.75001335144043`], List[29.960912883281708`, 50.15229543567091`], List[31.09769024431398`, 51.28907376527786`], List[32.49997329711914`, 51.28907376527786`], List[33.90225247562557`, 51.28907376527786`], List[35.03903371095657`, 50.15229543567091`], List[35.03903371095657`, 48.75001335144043`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 32.50002670288086`], List[35.03903371095657`, 31.097747524374427`], List[33.90225247562557`, 29.960966289043427`], List[32.49997329711914`, 29.960966289043427`], List[31.09769024431398`, 29.960966289043427`], List[29.960912883281708`, 31.097747524374427`], List[29.960912883281708`, 32.50002670288086`], List[29.960912883281708`, 33.90230975568602`], List[31.09769024431398`, 35.03908711671829`], List[32.49997329711914`, 35.03908711671829`], List[33.90225247562557`, 35.03908711671829`], List[35.03903371095657`, 33.90230975568602`], List[35.03903371095657`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 16.25004005432129`], List[35.03903371095657`, 14.847760875814856`], List[33.90225247562557`, 13.710979640483856`], List[32.49997329711914`, 13.710979640483856`], List[31.09769024431398`, 13.710979640483856`], List[29.960912883281708`, 14.847760875814856`], List[29.960912883281708`, 16.25004005432129`], List[29.960912883281708`, 17.65232310712645`], List[31.09769024431398`, 18.789100468158722`], List[32.49997329711914`, 18.789100468158722`], List[33.90225247562557`, 18.789100468158722`], List[35.03903371095657`, 17.65232310712645`], List[35.03903371095657`, 16.25004005432129`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 56.36719459295273`], List[49.2577720284462`, 54.96491250872225`], List[48.1209907931152`, 53.828134179115295`], List[46.718711614608765`, 53.828134179115295`], List[45.316428561803605`, 53.828134179115295`], List[44.17965120077133`, 54.96491250872225`], List[44.17965120077133`, 56.36719459295273`], List[44.17965120077133`, 57.76947716147055`], List[45.316428561803605`, 58.90625500679016`], List[46.718711614608765`, 58.90625500679016`], List[48.1209907931152`, 58.90625500679016`], List[49.2577720284462`, 57.76947716147055`], List[49.2577720284462`, 56.36719459295273`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 40.625020027160645`], List[49.2577720284462`, 39.222736974355485`], List[48.1209907931152`, 38.08595961332321`], List[46.718711614608765`, 38.08595961332321`], List[45.316428561803605`, 38.08595961332321`], List[44.17965120077133`, 39.222736974355485`], List[44.17965120077133`, 40.625020027160645`], List[44.17965120077133`, 42.027303079965804`], List[45.316428561803605`, 43.16408044099808`], List[46.718711614608765`, 43.16408044099808`], List[48.1209907931152`, 43.16408044099808`], List[49.2577720284462`, 42.027303079965804`], List[49.2577720284462`, 40.625020027160645`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 24.375033378601074`], List[49.2577720284462`, 22.97275420009464`], List[48.1209907931152`, 21.83597296476364`], List[46.718711614608765`, 21.83597296476364`], List[45.316428561803605`, 21.83597296476364`], List[44.17965120077133`, 22.97275420009464`], List[44.17965120077133`, 24.375033378601074`], List[44.17965120077133`, 25.777316431406234`], List[45.316428561803605`, 26.914093792438507`], List[46.718711614608765`, 26.914093792438507`], List[48.1209907931152`, 26.914093792438507`], List[49.2577720284462`, 25.777316431406234`], List[49.2577720284462`, 24.375033378601074`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 8.63285881280899`], List[49.2577720284462`, 7.230591257198739`], List[48.1209907931152`, 6.093798398971558`], List[46.718711614608765`, 6.093798398971558`], List[45.316428561803605`, 6.093798398971558`], List[44.17965120077133`, 7.230591257198739`], List[44.17965120077133`, 8.63285881280899`], List[44.17965120077133`, 10.035130242717969`], List[45.316428561803605`, 11.171919226646423`], List[46.718711614608765`, 11.171919226646423`], List[48.1209907931152`, 11.171919226646423`], List[49.2577720284462`, 10.035130242717969`], List[49.2577720284462`, 8.63285881280899`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[62.968698263168335`, 32.50002670288086`], List[62.968698263168335`, 31.097747524374427`], List[61.83190540494115`, 29.960966289043427`], List[60.4296378493309`, 29.960966289043427`], List[59.027366419421924`, 29.960966289043427`], List[57.89057743549347`, 31.097747524374427`], List[57.89057743549347`, 32.50002670288086`], List[57.89057743549347`, 33.90230975568602`], List[59.027366419421924`, 35.03908711671829`], List[60.4296378493309`, 35.03908711671829`], List[61.83190540494115`, 35.03908711671829`], List[62.968698263168335`, 33.90230975568602`], List[62.968698263168335`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]]], List[Rule[BaselinePosition, Scaled[0.15`]], Rule[ImageSize, 10], Rule[ImageSize, List[Automatic, 35]]]], StyleBox[RowBox[List["QuantumState", " "]], Rule[ShowAutoStyles, False], Rule[ShowStringCharacters, False], Rule[FontSize, Times[0.9`, Inherited]], Rule[FontColor, GrayLevel[0.1`]]]]], Rule[GridBoxSpacings, List[Rule["Columns", List[List[0.25`]]]]]], Rule[Alignment, List[Left, Baseline]], Rule[BaselinePosition, Baseline], Rule[FrameMargins, List[List[3, 0], List[0, 0]]], Rule[BaseStyle, List[Rule[LineSpacing, List[0, 0]], Rule[LineBreakWithin, False]]]], RowBox[List["PacletSymbol", "[", RowBox[List["\"Wolfram/QuantumFramework\"", ",", "\"QuantumState\""]], "]"]], Rule[TooltipStyle, List[Rule[ShowAutoStyles, True], Rule[ShowStringCharacters, True]]]], Function[Annotation[Slot[1], Style[Defer[PacletSymbol["Wolfram/QuantumFramework", "QuantumState"]], Rule[ShowStringCharacters, True]], "Tooltip"]]], Rule[Background, RGBColor[0.968`, 0.976`, 0.984`]], Rule[BaselinePosition, Baseline], Rule[DefaultBaseStyle, List[]], Rule[FrameMargins, List[List[0, 0], List[1, 1]]], Rule[FrameStyle, RGBColor[0.831`, 0.847`, 0.85`]], Rule[RoundingRadius, 4]], PacletSymbol["Wolfram/QuantumFramework", "QuantumState"], Rule[Selectable, False], Rule[SelectWithContents, True], Rule[BoxID, "PacletSymbolBox"]][{"Register", 3, i}], {i, 2^3 - 1, 0, -1}]},
TableForm[
Transpose[{#["Formula"] & /@ index, phaseOracle[#]["Formula"] & /@ index}], TableHeadings -> {None, {"|x>", "(-1\!\(\*SuperscriptBox[\()\), \(f \((x)\)\)]\)|x>"}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/56a2011030747a8d.png)
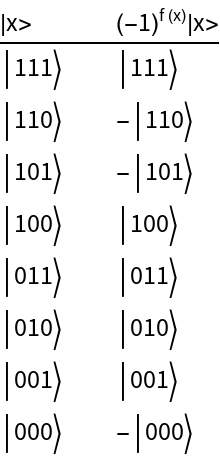
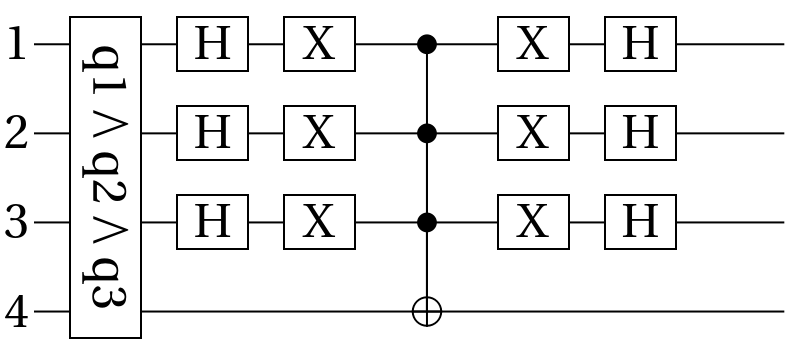
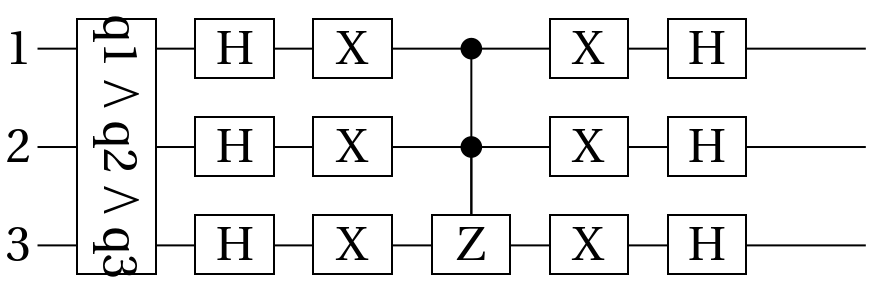
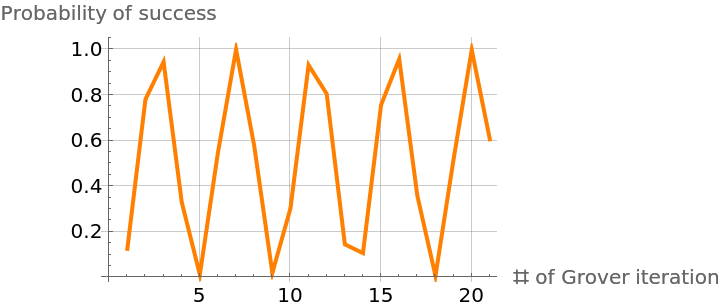
![]() where M is number of correct solutions out of total N after k steps
where M is number of correct solutions out of total N after k steps![]() . The output is
. The output is ![]() .
We will consider a phase shift as the unitary operator where we aim to find the phase θ:
.
We will consider a phase shift as the unitary operator where we aim to find the phase θ:![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/c6baafa4-5f70-45de-a5dc-d6a98d1c4578"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/632d885a87deda6a.png)
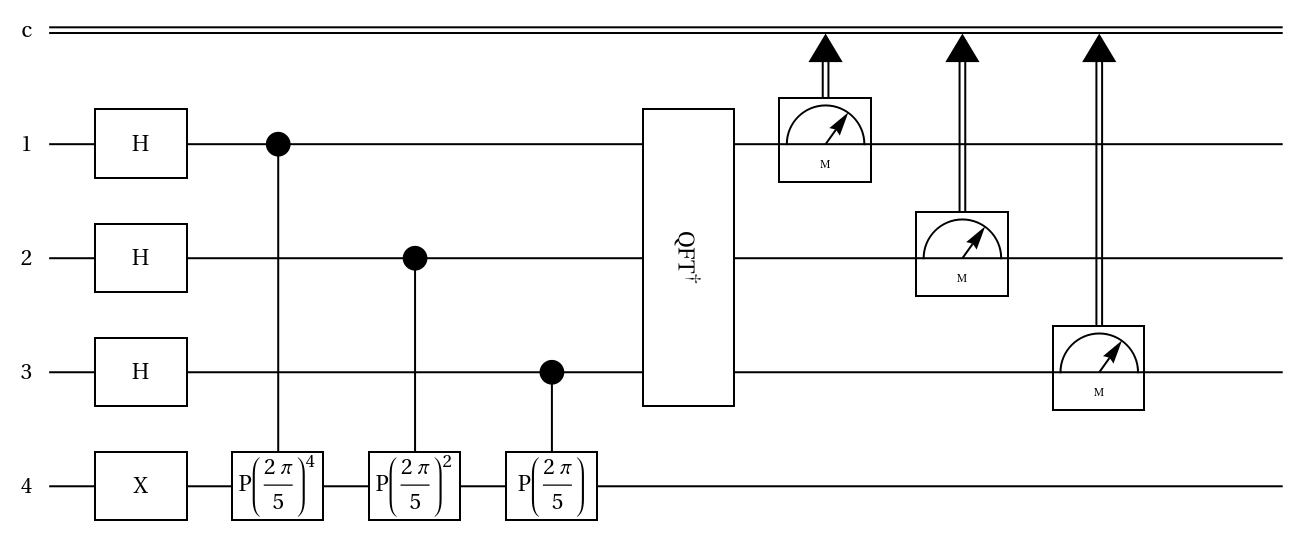
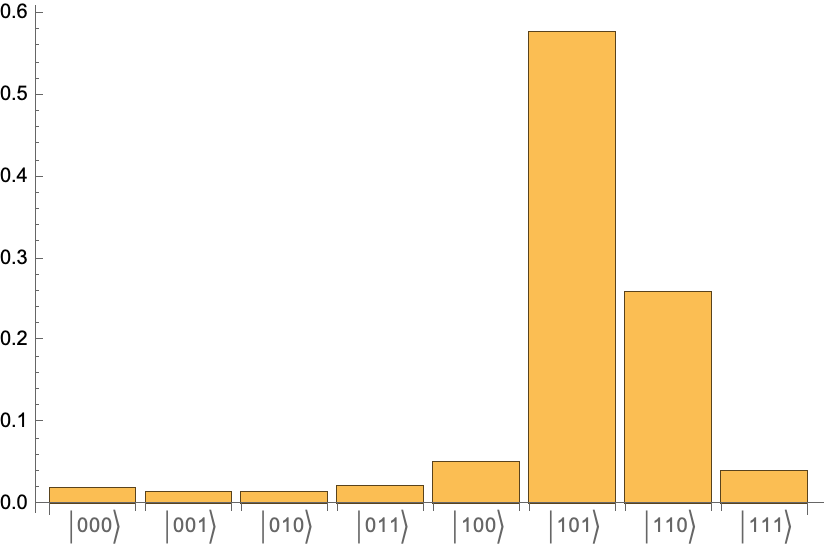
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/40bab72e-bb9c-4672-8912-0610b8c8f782"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/3f8d7d843bfa4990.png)
![]() , where the subscript indicates the number of qubits.
, where the subscript indicates the number of qubits.![]() is a nontrivial factor of .
is a nontrivial factor of .![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/95d3ec91-c8f0-416b-84f0-d97fa719de94"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/42f86725c1beefad.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/2649d7df-714d-4962-bcca-94f48edff63a"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/1f0f444e1058606b.png)
![]() :
: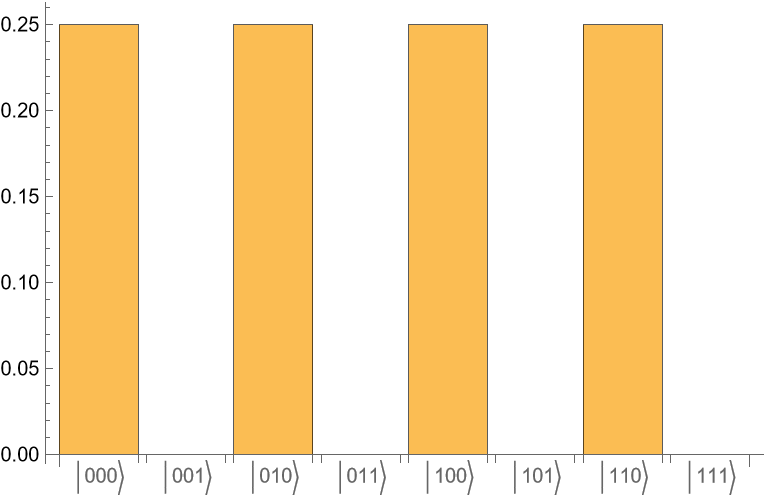
![]() ,
, ![]() ,
, ![]() , and
, and ![]() . If one obtains
. If one obtains ![]() , one must repeat the protocol. Otherwise:
, one must repeat the protocol. Otherwise:![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/935982cc-87df-4602-920e-4c213b482dd4"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/1cb3d5ae84da786c.png)
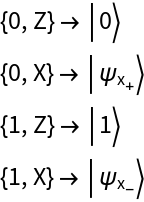
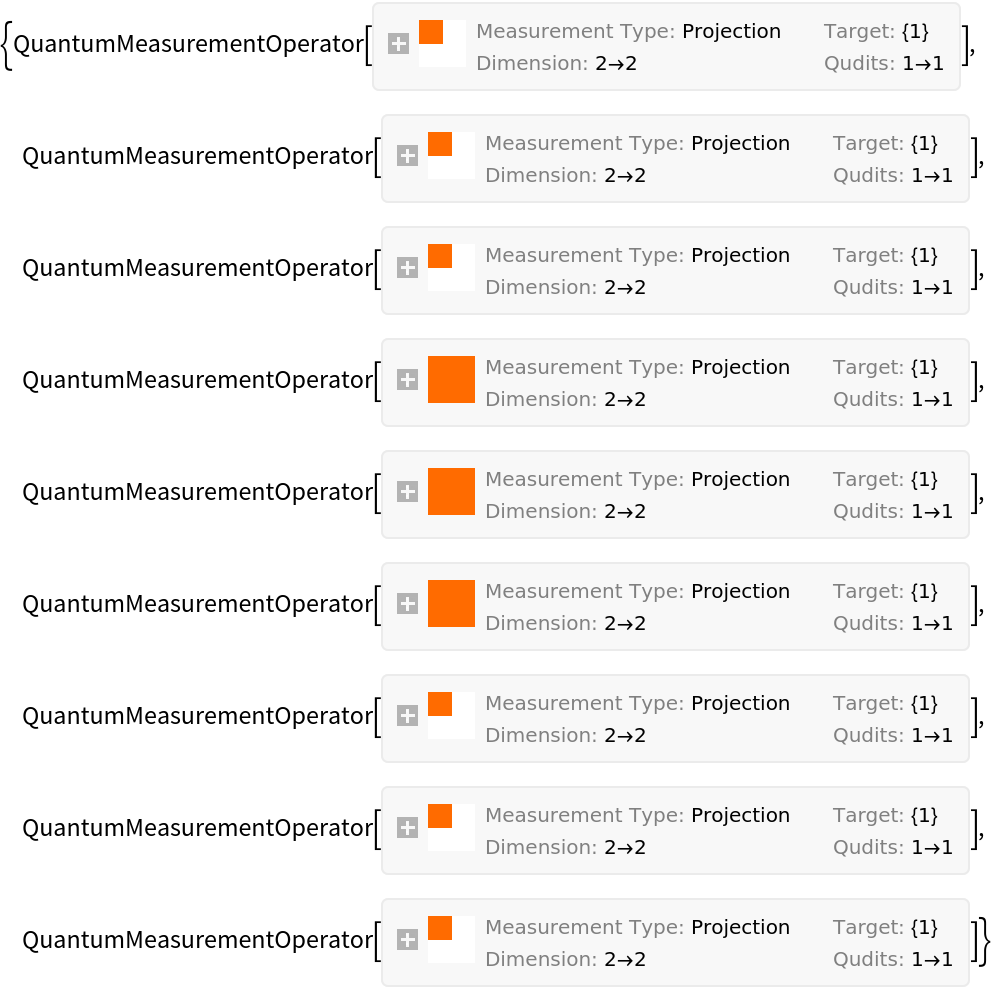
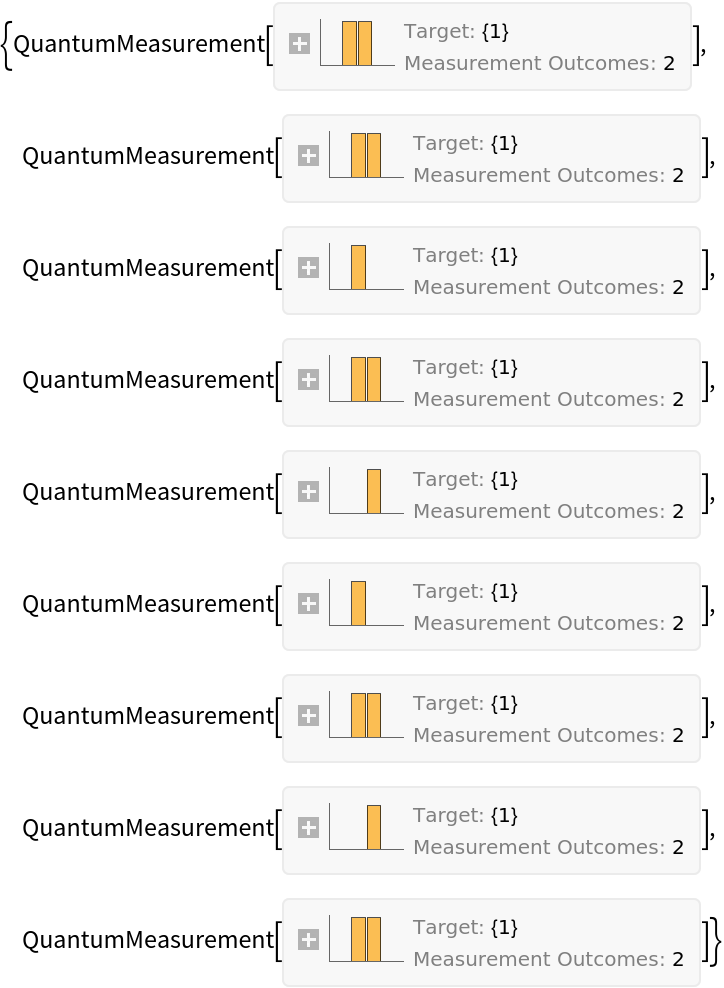
![bobRealization = #["SimulatedMeasurement"] & /@ MapThread[#1[#2] &, {InterpretationBox[FrameBox[TagBox[TooltipBox[PaneBox[GridBox[List[List[GraphicsBox[List[Thickness[0.015384615384615385`], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[19.29685914516449`, 56.875006675720215`], List[32.49997329711914`, 64.49218791723251`], List[45.70308744907379`, 56.875006675720215`], List[32.49997329711914`, 49.257825434207916`], List[19.29685914516449`, 56.875006675720215`]], List[List[21.328107476234436`, 56.875006675720215`], List[32.49997329711914`, 63.32422015108166`], List[43.671839118003845`, 56.875006675720215`], List[32.49997329711914`, 50.42579283714326`], List[21.328107476234436`, 56.875006675720215`]], List[List[33.00778537988663`, 33.26174482703209`], List[33.00778537988663`, 48.496107310056686`], List[46.21089953184128`, 56.113288551568985`], List[46.21089953184128`, 40.87892606854439`], List[33.00778537988663`, 33.26174482703209`]]]]], List[FaceForm[RGBColor[0.7019607843137254`, 0.6039215686274509`, 0.788235294117647`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[31.992161214351654`, 33.26174482703209`], List[18.789047062397003`, 40.87892606854439`], List[18.789047062397003`, 56.113288551568985`], List[31.992161214351654`, 48.496107310056686`], List[31.992161214351654`, 33.26174482703209`]]]]], List[FaceForm[RGBColor[0.5372549019607843`, 0.403921568627451`, 0.6745098039215687`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[17.77342289686203`, 8.886764854192734`], List[4.570308744907379`, 16.503946095705032`], List[4.570308744907379`, 31.73830857872963`], List[17.77342289686203`, 24.12112733721733`], List[17.77342289686203`, 8.886764854192734`]], List[List[16.757798731327057`, 10.664107143878937`], List[5.585932910442352`, 17.113319045306525`], List[5.585932910442352`, 29.960966289043427`], List[16.757798731327057`, 23.511754387615838`], List[16.757798731327057`, 10.664107143878937`]], List[List[31.484349131584167`, 32.50002670288086`], List[18.281234979629517`, 40.11720794439316`], List[5.078120827674866`, 32.50002670288086`], List[18.281234979629517`, 24.88284546136856`], List[31.484349131584167`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.6352941176470588`, 0.7333333333333333`, 0.8313725490196079`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[31.992161214351654`, 31.73830857872963`], List[18.789047062397003`, 24.12112733721733`], List[18.789047062397003`, 8.886764854192734`], List[31.992161214351654`, 16.503946095705032`], List[31.992161214351654`, 31.73830857872963`]]]]], List[FaceForm[RGBColor[0.2901960784313726`, 0.40784313725490196`, 0.5764705882352941`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[47.22652369737625`, 8.886764854192734`], List[47.22652369737625`, 24.12112733721733`], List[60.4296378493309`, 31.73830857872963`], List[60.4296378493309`, 16.503946095705032`], List[47.22652369737625`, 8.886764854192734`]], List[List[48.242147862911224`, 10.664107143878937`], List[48.242147862911224`, 23.511754387615838`], List[59.41401368379593`, 29.960966289043427`], List[59.41401368379593`, 17.113319045306525`], List[48.242147862911224`, 10.664107143878937`]], List[List[33.515597462654114`, 32.50002670288086`], List[46.718711614608765`, 40.11720794439316`], List[59.921825766563416`, 32.50002670288086`], List[46.718711614608765`, 24.88284546136856`], List[33.515597462654114`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.6`, 0.6`, 0.37254901960784315`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[33.00778537988663`, 31.73830857872963`], List[33.00778537988663`, 16.503946095705032`], List[46.21089953184128`, 8.886764854192734`], List[46.21089953184128`, 24.12112733721733`], List[33.00778537988663`, 31.73830857872963`]]]]], List[FaceForm[RGBColor[0.396078431372549`, 0.6039215686274509`, 0.30196078431372547`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[5.585932910442352`, 35.03908711671829`], List[5.585932910442352`, 47.88673242330583`], List[16.757798731327057`, 54.33594626188278`], List[16.757798731327057`, 41.488300955295244`], List[5.585932910442352`, 35.03908711671829`]], List[List[4.570308744907379`, 33.26174482703209`], List[4.570308744907379`, 48.496107310056686`], List[17.77342289686203`, 56.113288551568985`], List[17.77342289686203`, 40.87892606854439`], List[4.570308744907379`, 33.26174482703209`]], List[List[60.4296378493309`, 33.26174482703209`], List[47.22652369737625`, 40.87892606854439`], List[47.22652369737625`, 56.113288551568985`], List[60.4296378493309`, 48.496107310056686`], List[60.4296378493309`, 33.26174482703209`]], List[List[59.41401368379593`, 35.03908711671829`], List[48.242147862911224`, 41.488300955295244`], List[48.242147862911224`, 54.33594626188278`], List[59.41401368379593`, 47.88673242330583`], List[59.41401368379593`, 35.03908711671829`]], List[List[19.29685914516449`, 8.125046730041504`], List[32.49997329711914`, 15.742227971553802`], List[45.70308744907379`, 8.125046730041504`], List[32.49997329711914`, 0.5078654885292053`], List[19.29685914516449`, 8.125046730041504`]], List[List[21.328107476234436`, 8.125046730041504`], List[32.49997329711914`, 14.574258631469093`], List[43.671839118003845`, 8.125046730041504`], List[32.49997329711914`, 1.6758348286139153`], List[21.328107476234436`, 8.125046730041504`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[7.109369158744812`, 32.50002670288086`], List[7.109369158744812`, 31.097747524374427`], List[5.972591313425198`, 29.960966289043427`], List[4.570308744907379`, 29.960966289043427`], List[3.168024481383867`, 29.960966289043427`], List[2.0312483310699463`, 31.097747524374427`], List[2.0312483310699463`, 32.50002670288086`], List[2.0312483310699463`, 33.90230975568602`], List[3.168024481383867`, 35.03908711671829`], List[4.570308744907379`, 35.03908711671829`], List[5.972591313425198`, 35.03908711671829`], List[7.109369158744812`, 33.90230975568602`], List[7.109369158744812`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 56.36719459295273`], List[20.82029539346695`, 54.96491250872225`], List[19.683518032434677`, 53.828134179115295`], List[18.281234979629517`, 53.828134179115295`], List[16.878951926824357`, 53.828134179115295`], List[15.742174565792084`, 54.96491250872225`], List[15.742174565792084`, 56.36719459295273`], List[15.742174565792084`, 57.76947716147055`], List[16.878951926824357`, 58.90625500679016`], List[18.281234979629517`, 58.90625500679016`], List[19.683518032434677`, 58.90625500679016`], List[20.82029539346695`, 57.76947716147055`], List[20.82029539346695`, 56.36719459295273`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 40.625020027160645`], List[20.82029539346695`, 39.222736974355485`], List[19.683518032434677`, 38.08595961332321`], List[18.281234979629517`, 38.08595961332321`], List[16.878951926824357`, 38.08595961332321`], List[15.742174565792084`, 39.222736974355485`], List[15.742174565792084`, 40.625020027160645`], List[15.742174565792084`, 42.027303079965804`], List[16.878951926824357`, 43.16408044099808`], List[18.281234979629517`, 43.16408044099808`], List[19.683518032434677`, 43.16408044099808`], List[20.82029539346695`, 42.027303079965804`], List[20.82029539346695`, 40.625020027160645`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 24.375033378601074`], List[20.82029539346695`, 22.97275420009464`], List[19.683518032434677`, 21.83597296476364`], List[18.281234979629517`, 21.83597296476364`], List[16.878951926824357`, 21.83597296476364`], List[15.742174565792084`, 22.97275420009464`], List[15.742174565792084`, 24.375033378601074`], List[15.742174565792084`, 25.777316431406234`], List[16.878951926824357`, 26.914093792438507`], List[18.281234979629517`, 26.914093792438507`], List[19.683518032434677`, 26.914093792438507`], List[20.82029539346695`, 25.777316431406234`], List[20.82029539346695`, 24.375033378601074`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 8.63285881280899`], List[20.82029539346695`, 7.230591257198739`], List[19.683518032434677`, 6.093798398971558`], List[18.281234979629517`, 6.093798398971558`], List[16.878951926824357`, 6.093798398971558`], List[15.742174565792084`, 7.230591257198739`], List[15.742174565792084`, 8.63285881280899`], List[15.742174565792084`, 10.035130242717969`], List[16.878951926824357`, 11.171919226646423`], List[18.281234979629517`, 11.171919226646423`], List[19.683518032434677`, 11.171919226646423`], List[20.82029539346695`, 10.035130242717969`], List[20.82029539346695`, 8.63285881280899`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 48.75001335144043`], List[35.03903371095657`, 47.34773029863527`], List[33.90225247562557`, 46.210952937603`], List[32.49997329711914`, 46.210952937603`], List[31.09769024431398`, 46.210952937603`], List[29.960912883281708`, 47.34773029863527`], List[29.960912883281708`, 48.75001335144043`], List[29.960912883281708`, 50.15229543567091`], List[31.09769024431398`, 51.28907376527786`], List[32.49997329711914`, 51.28907376527786`], List[33.90225247562557`, 51.28907376527786`], List[35.03903371095657`, 50.15229543567091`], List[35.03903371095657`, 48.75001335144043`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 32.50002670288086`], List[35.03903371095657`, 31.097747524374427`], List[33.90225247562557`, 29.960966289043427`], List[32.49997329711914`, 29.960966289043427`], List[31.09769024431398`, 29.960966289043427`], List[29.960912883281708`, 31.097747524374427`], List[29.960912883281708`, 32.50002670288086`], List[29.960912883281708`, 33.90230975568602`], List[31.09769024431398`, 35.03908711671829`], List[32.49997329711914`, 35.03908711671829`], List[33.90225247562557`, 35.03908711671829`], List[35.03903371095657`, 33.90230975568602`], List[35.03903371095657`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 16.25004005432129`], List[35.03903371095657`, 14.847760875814856`], List[33.90225247562557`, 13.710979640483856`], List[32.49997329711914`, 13.710979640483856`], List[31.09769024431398`, 13.710979640483856`], List[29.960912883281708`, 14.847760875814856`], List[29.960912883281708`, 16.25004005432129`], List[29.960912883281708`, 17.65232310712645`], List[31.09769024431398`, 18.789100468158722`], List[32.49997329711914`, 18.789100468158722`], List[33.90225247562557`, 18.789100468158722`], List[35.03903371095657`, 17.65232310712645`], List[35.03903371095657`, 16.25004005432129`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 56.36719459295273`], List[49.2577720284462`, 54.96491250872225`], List[48.1209907931152`, 53.828134179115295`], List[46.718711614608765`, 53.828134179115295`], List[45.316428561803605`, 53.828134179115295`], List[44.17965120077133`, 54.96491250872225`], List[44.17965120077133`, 56.36719459295273`], List[44.17965120077133`, 57.76947716147055`], List[45.316428561803605`, 58.90625500679016`], List[46.718711614608765`, 58.90625500679016`], List[48.1209907931152`, 58.90625500679016`], List[49.2577720284462`, 57.76947716147055`], List[49.2577720284462`, 56.36719459295273`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 40.625020027160645`], List[49.2577720284462`, 39.222736974355485`], List[48.1209907931152`, 38.08595961332321`], List[46.718711614608765`, 38.08595961332321`], List[45.316428561803605`, 38.08595961332321`], List[44.17965120077133`, 39.222736974355485`], List[44.17965120077133`, 40.625020027160645`], List[44.17965120077133`, 42.027303079965804`], List[45.316428561803605`, 43.16408044099808`], List[46.718711614608765`, 43.16408044099808`], List[48.1209907931152`, 43.16408044099808`], List[49.2577720284462`, 42.027303079965804`], List[49.2577720284462`, 40.625020027160645`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 24.375033378601074`], List[49.2577720284462`, 22.97275420009464`], List[48.1209907931152`, 21.83597296476364`], List[46.718711614608765`, 21.83597296476364`], List[45.316428561803605`, 21.83597296476364`], List[44.17965120077133`, 22.97275420009464`], List[44.17965120077133`, 24.375033378601074`], List[44.17965120077133`, 25.777316431406234`], List[45.316428561803605`, 26.914093792438507`], List[46.718711614608765`, 26.914093792438507`], List[48.1209907931152`, 26.914093792438507`], List[49.2577720284462`, 25.777316431406234`], List[49.2577720284462`, 24.375033378601074`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 8.63285881280899`], List[49.2577720284462`, 7.230591257198739`], List[48.1209907931152`, 6.093798398971558`], List[46.718711614608765`, 6.093798398971558`], List[45.316428561803605`, 6.093798398971558`], List[44.17965120077133`, 7.230591257198739`], List[44.17965120077133`, 8.63285881280899`], List[44.17965120077133`, 10.035130242717969`], List[45.316428561803605`, 11.171919226646423`], List[46.718711614608765`, 11.171919226646423`], List[48.1209907931152`, 11.171919226646423`], List[49.2577720284462`, 10.035130242717969`], List[49.2577720284462`, 8.63285881280899`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[62.968698263168335`, 32.50002670288086`], List[62.968698263168335`, 31.097747524374427`], List[61.83190540494115`, 29.960966289043427`], List[60.4296378493309`, 29.960966289043427`], List[59.027366419421924`, 29.960966289043427`], List[57.89057743549347`, 31.097747524374427`], List[57.89057743549347`, 32.50002670288086`], List[57.89057743549347`, 33.90230975568602`], List[59.027366419421924`, 35.03908711671829`], List[60.4296378493309`, 35.03908711671829`], List[61.83190540494115`, 35.03908711671829`], List[62.968698263168335`, 33.90230975568602`], List[62.968698263168335`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]]], List[Rule[BaselinePosition, Scaled[0.15`]], Rule[ImageSize, 10], Rule[ImageSize, List[Automatic, 35]]]], StyleBox[RowBox[List["QuantumMeasurementOperator", " "]], Rule[ShowAutoStyles, False], Rule[ShowStringCharacters, False], Rule[FontSize, Times[0.9`, Inherited]], Rule[FontColor, GrayLevel[0.1`]]]]], Rule[GridBoxSpacings, List[Rule["Columns", List[List[0.25`]]]]]], Rule[Alignment, List[Left, Baseline]], Rule[BaselinePosition, Baseline], Rule[FrameMargins, List[List[3, 0], List[0, 0]]], Rule[BaseStyle, List[Rule[LineSpacing, List[0, 0]], Rule[LineBreakWithin, False]]]], RowBox[List["PacletSymbol", "[", RowBox[List["\"Wolfram/QuantumFramework\"", ",", "\"QuantumMeasurementOperator\""]], "]"]], Rule[TooltipStyle, List[Rule[ShowAutoStyles, True], Rule[ShowStringCharacters, True]]]], Function[Annotation[Slot[1], Style[Defer[PacletSymbol["Wolfram/QuantumFramework", "QuantumMeasurementOperator"]], Rule[ShowStringCharacters, True]], "Tooltip"]]], Rule[Background, RGBColor[0.968`, 0.976`, 0.984`]], Rule[BaselinePosition, Baseline], Rule[DefaultBaseStyle, List[]], Rule[FrameMargins, List[List[0, 0], List[1, 1]]], Rule[FrameStyle, RGBColor[0.831`, 0.847`, 0.85`]], Rule[RoundingRadius, 4]], PacletSymbol["Wolfram/QuantumFramework", "QuantumMeasurementOperator"], Rule[Selectable, False], Rule[SelectWithContents, True], Rule[BoxID, "PacletSymbolBox"]] /@ bobBases, aliceQubits}]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/2d1bd42ee3ac6fb9.png)
![add[{x_, y_}] := Module[{aliceBit, aliceBase, aliceQubit, bobBase, bobBit},
aliceBit = RandomChoice[{0, 1}];
aliceBase = RandomChoice[{"Z", "X"}];
aliceQubit = aliceProtocol[{aliceBit, aliceBase}];
bobBase = RandomChoice[{"Z", "X"}];
bobBit = InterpretationBox[FrameBox[TagBox[TooltipBox[PaneBox[GridBox[List[List[GraphicsBox[List[Thickness[0.015384615384615385`], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[19.29685914516449`, 56.875006675720215`], List[32.49997329711914`, 64.49218791723251`], List[45.70308744907379`, 56.875006675720215`], List[32.49997329711914`, 49.257825434207916`], List[19.29685914516449`, 56.875006675720215`]], List[List[21.328107476234436`, 56.875006675720215`], List[32.49997329711914`, 63.32422015108166`], List[43.671839118003845`, 56.875006675720215`], List[32.49997329711914`, 50.42579283714326`], List[21.328107476234436`, 56.875006675720215`]], List[List[33.00778537988663`, 33.26174482703209`], List[33.00778537988663`, 48.496107310056686`], List[46.21089953184128`, 56.113288551568985`], List[46.21089953184128`, 40.87892606854439`], List[33.00778537988663`, 33.26174482703209`]]]]], List[FaceForm[RGBColor[0.7019607843137254`, 0.6039215686274509`, 0.788235294117647`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[31.992161214351654`, 33.26174482703209`], List[18.789047062397003`, 40.87892606854439`], List[18.789047062397003`, 56.113288551568985`], List[31.992161214351654`, 48.496107310056686`], List[31.992161214351654`, 33.26174482703209`]]]]], List[FaceForm[RGBColor[0.5372549019607843`, 0.403921568627451`, 0.6745098039215687`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[17.77342289686203`, 8.886764854192734`], List[4.570308744907379`, 16.503946095705032`], List[4.570308744907379`, 31.73830857872963`], List[17.77342289686203`, 24.12112733721733`], List[17.77342289686203`, 8.886764854192734`]], List[List[16.757798731327057`, 10.664107143878937`], List[5.585932910442352`, 17.113319045306525`], List[5.585932910442352`, 29.960966289043427`], List[16.757798731327057`, 23.511754387615838`], List[16.757798731327057`, 10.664107143878937`]], List[List[31.484349131584167`, 32.50002670288086`], List[18.281234979629517`, 40.11720794439316`], List[5.078120827674866`, 32.50002670288086`], List[18.281234979629517`, 24.88284546136856`], List[31.484349131584167`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.6352941176470588`, 0.7333333333333333`, 0.8313725490196079`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[31.992161214351654`, 31.73830857872963`], List[18.789047062397003`, 24.12112733721733`], List[18.789047062397003`, 8.886764854192734`], List[31.992161214351654`, 16.503946095705032`], List[31.992161214351654`, 31.73830857872963`]]]]], List[FaceForm[RGBColor[0.2901960784313726`, 0.40784313725490196`, 0.5764705882352941`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[47.22652369737625`, 8.886764854192734`], List[47.22652369737625`, 24.12112733721733`], List[60.4296378493309`, 31.73830857872963`], List[60.4296378493309`, 16.503946095705032`], List[47.22652369737625`, 8.886764854192734`]], List[List[48.242147862911224`, 10.664107143878937`], List[48.242147862911224`, 23.511754387615838`], List[59.41401368379593`, 29.960966289043427`], List[59.41401368379593`, 17.113319045306525`], List[48.242147862911224`, 10.664107143878937`]], List[List[33.515597462654114`, 32.50002670288086`], List[46.718711614608765`, 40.11720794439316`], List[59.921825766563416`, 32.50002670288086`], List[46.718711614608765`, 24.88284546136856`], List[33.515597462654114`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.6`, 0.6`, 0.37254901960784315`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[33.00778537988663`, 31.73830857872963`], List[33.00778537988663`, 16.503946095705032`], List[46.21089953184128`, 8.886764854192734`], List[46.21089953184128`, 24.12112733721733`], List[33.00778537988663`, 31.73830857872963`]]]]], List[FaceForm[RGBColor[0.396078431372549`, 0.6039215686274509`, 0.30196078431372547`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]], List[List[0, 2, 0], List[0, 1, 0], List[0, 1, 0], List[0, 1, 0]]], List[List[List[5.585932910442352`, 35.03908711671829`], List[5.585932910442352`, 47.88673242330583`], List[16.757798731327057`, 54.33594626188278`], List[16.757798731327057`, 41.488300955295244`], List[5.585932910442352`, 35.03908711671829`]], List[List[4.570308744907379`, 33.26174482703209`], List[4.570308744907379`, 48.496107310056686`], List[17.77342289686203`, 56.113288551568985`], List[17.77342289686203`, 40.87892606854439`], List[4.570308744907379`, 33.26174482703209`]], List[List[60.4296378493309`, 33.26174482703209`], List[47.22652369737625`, 40.87892606854439`], List[47.22652369737625`, 56.113288551568985`], List[60.4296378493309`, 48.496107310056686`], List[60.4296378493309`, 33.26174482703209`]], List[List[59.41401368379593`, 35.03908711671829`], List[48.242147862911224`, 41.488300955295244`], List[48.242147862911224`, 54.33594626188278`], List[59.41401368379593`, 47.88673242330583`], List[59.41401368379593`, 35.03908711671829`]], List[List[19.29685914516449`, 8.125046730041504`], List[32.49997329711914`, 15.742227971553802`], List[45.70308744907379`, 8.125046730041504`], List[32.49997329711914`, 0.5078654885292053`], List[19.29685914516449`, 8.125046730041504`]], List[List[21.328107476234436`, 8.125046730041504`], List[32.49997329711914`, 14.574258631469093`], List[43.671839118003845`, 8.125046730041504`], List[32.49997329711914`, 1.6758348286139153`], List[21.328107476234436`, 8.125046730041504`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[7.109369158744812`, 32.50002670288086`], List[7.109369158744812`, 31.097747524374427`], List[5.972591313425198`, 29.960966289043427`], List[4.570308744907379`, 29.960966289043427`], List[3.168024481383867`, 29.960966289043427`], List[2.0312483310699463`, 31.097747524374427`], List[2.0312483310699463`, 32.50002670288086`], List[2.0312483310699463`, 33.90230975568602`], List[3.168024481383867`, 35.03908711671829`], List[4.570308744907379`, 35.03908711671829`], List[5.972591313425198`, 35.03908711671829`], List[7.109369158744812`, 33.90230975568602`], List[7.109369158744812`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 56.36719459295273`], List[20.82029539346695`, 54.96491250872225`], List[19.683518032434677`, 53.828134179115295`], List[18.281234979629517`, 53.828134179115295`], List[16.878951926824357`, 53.828134179115295`], List[15.742174565792084`, 54.96491250872225`], List[15.742174565792084`, 56.36719459295273`], List[15.742174565792084`, 57.76947716147055`], List[16.878951926824357`, 58.90625500679016`], List[18.281234979629517`, 58.90625500679016`], List[19.683518032434677`, 58.90625500679016`], List[20.82029539346695`, 57.76947716147055`], List[20.82029539346695`, 56.36719459295273`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 40.625020027160645`], List[20.82029539346695`, 39.222736974355485`], List[19.683518032434677`, 38.08595961332321`], List[18.281234979629517`, 38.08595961332321`], List[16.878951926824357`, 38.08595961332321`], List[15.742174565792084`, 39.222736974355485`], List[15.742174565792084`, 40.625020027160645`], List[15.742174565792084`, 42.027303079965804`], List[16.878951926824357`, 43.16408044099808`], List[18.281234979629517`, 43.16408044099808`], List[19.683518032434677`, 43.16408044099808`], List[20.82029539346695`, 42.027303079965804`], List[20.82029539346695`, 40.625020027160645`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 24.375033378601074`], List[20.82029539346695`, 22.97275420009464`], List[19.683518032434677`, 21.83597296476364`], List[18.281234979629517`, 21.83597296476364`], List[16.878951926824357`, 21.83597296476364`], List[15.742174565792084`, 22.97275420009464`], List[15.742174565792084`, 24.375033378601074`], List[15.742174565792084`, 25.777316431406234`], List[16.878951926824357`, 26.914093792438507`], List[18.281234979629517`, 26.914093792438507`], List[19.683518032434677`, 26.914093792438507`], List[20.82029539346695`, 25.777316431406234`], List[20.82029539346695`, 24.375033378601074`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[20.82029539346695`, 8.63285881280899`], List[20.82029539346695`, 7.230591257198739`], List[19.683518032434677`, 6.093798398971558`], List[18.281234979629517`, 6.093798398971558`], List[16.878951926824357`, 6.093798398971558`], List[15.742174565792084`, 7.230591257198739`], List[15.742174565792084`, 8.63285881280899`], List[15.742174565792084`, 10.035130242717969`], List[16.878951926824357`, 11.171919226646423`], List[18.281234979629517`, 11.171919226646423`], List[19.683518032434677`, 11.171919226646423`], List[20.82029539346695`, 10.035130242717969`], List[20.82029539346695`, 8.63285881280899`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 48.75001335144043`], List[35.03903371095657`, 47.34773029863527`], List[33.90225247562557`, 46.210952937603`], List[32.49997329711914`, 46.210952937603`], List[31.09769024431398`, 46.210952937603`], List[29.960912883281708`, 47.34773029863527`], List[29.960912883281708`, 48.75001335144043`], List[29.960912883281708`, 50.15229543567091`], List[31.09769024431398`, 51.28907376527786`], List[32.49997329711914`, 51.28907376527786`], List[33.90225247562557`, 51.28907376527786`], List[35.03903371095657`, 50.15229543567091`], List[35.03903371095657`, 48.75001335144043`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 32.50002670288086`], List[35.03903371095657`, 31.097747524374427`], List[33.90225247562557`, 29.960966289043427`], List[32.49997329711914`, 29.960966289043427`], List[31.09769024431398`, 29.960966289043427`], List[29.960912883281708`, 31.097747524374427`], List[29.960912883281708`, 32.50002670288086`], List[29.960912883281708`, 33.90230975568602`], List[31.09769024431398`, 35.03908711671829`], List[32.49997329711914`, 35.03908711671829`], List[33.90225247562557`, 35.03908711671829`], List[35.03903371095657`, 33.90230975568602`], List[35.03903371095657`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[35.03903371095657`, 16.25004005432129`], List[35.03903371095657`, 14.847760875814856`], List[33.90225247562557`, 13.710979640483856`], List[32.49997329711914`, 13.710979640483856`], List[31.09769024431398`, 13.710979640483856`], List[29.960912883281708`, 14.847760875814856`], List[29.960912883281708`, 16.25004005432129`], List[29.960912883281708`, 17.65232310712645`], List[31.09769024431398`, 18.789100468158722`], List[32.49997329711914`, 18.789100468158722`], List[33.90225247562557`, 18.789100468158722`], List[35.03903371095657`, 17.65232310712645`], List[35.03903371095657`, 16.25004005432129`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 56.36719459295273`], List[49.2577720284462`, 54.96491250872225`], List[48.1209907931152`, 53.828134179115295`], List[46.718711614608765`, 53.828134179115295`], List[45.316428561803605`, 53.828134179115295`], List[44.17965120077133`, 54.96491250872225`], List[44.17965120077133`, 56.36719459295273`], List[44.17965120077133`, 57.76947716147055`], List[45.316428561803605`, 58.90625500679016`], List[46.718711614608765`, 58.90625500679016`], List[48.1209907931152`, 58.90625500679016`], List[49.2577720284462`, 57.76947716147055`], List[49.2577720284462`, 56.36719459295273`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 40.625020027160645`], List[49.2577720284462`, 39.222736974355485`], List[48.1209907931152`, 38.08595961332321`], List[46.718711614608765`, 38.08595961332321`], List[45.316428561803605`, 38.08595961332321`], List[44.17965120077133`, 39.222736974355485`], List[44.17965120077133`, 40.625020027160645`], List[44.17965120077133`, 42.027303079965804`], List[45.316428561803605`, 43.16408044099808`], List[46.718711614608765`, 43.16408044099808`], List[48.1209907931152`, 43.16408044099808`], List[49.2577720284462`, 42.027303079965804`], List[49.2577720284462`, 40.625020027160645`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 24.375033378601074`], List[49.2577720284462`, 22.97275420009464`], List[48.1209907931152`, 21.83597296476364`], List[46.718711614608765`, 21.83597296476364`], List[45.316428561803605`, 21.83597296476364`], List[44.17965120077133`, 22.97275420009464`], List[44.17965120077133`, 24.375033378601074`], List[44.17965120077133`, 25.777316431406234`], List[45.316428561803605`, 26.914093792438507`], List[46.718711614608765`, 26.914093792438507`], List[48.1209907931152`, 26.914093792438507`], List[49.2577720284462`, 25.777316431406234`], List[49.2577720284462`, 24.375033378601074`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[49.2577720284462`, 8.63285881280899`], List[49.2577720284462`, 7.230591257198739`], List[48.1209907931152`, 6.093798398971558`], List[46.718711614608765`, 6.093798398971558`], List[45.316428561803605`, 6.093798398971558`], List[44.17965120077133`, 7.230591257198739`], List[44.17965120077133`, 8.63285881280899`], List[44.17965120077133`, 10.035130242717969`], List[45.316428561803605`, 11.171919226646423`], List[46.718711614608765`, 11.171919226646423`], List[48.1209907931152`, 11.171919226646423`], List[49.2577720284462`, 10.035130242717969`], List[49.2577720284462`, 8.63285881280899`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]], StyleBox[List[FilledCurveBox[List[List[List[1, 4, 3], List[1, 3, 3], List[1, 3, 3], List[1, 3, 3]]], List[List[List[62.968698263168335`, 32.50002670288086`], List[62.968698263168335`, 31.097747524374427`], List[61.83190540494115`, 29.960966289043427`], List[60.4296378493309`, 29.960966289043427`], List[59.027366419421924`, 29.960966289043427`], List[57.89057743549347`, 31.097747524374427`], List[57.89057743549347`, 32.50002670288086`], List[57.89057743549347`, 33.90230975568602`], List[59.027366419421924`, 35.03908711671829`], List[60.4296378493309`, 35.03908711671829`], List[61.83190540494115`, 35.03908711671829`], List[62.968698263168335`, 33.90230975568602`], List[62.968698263168335`, 32.50002670288086`]]]]], List[FaceForm[RGBColor[0.9607843137254902`, 0.5098039215686274`, 0.20784313725490197`, 1.`]]], Rule[StripOnInput, False]]], List[Rule[BaselinePosition, Scaled[0.15`]], Rule[ImageSize, 10], Rule[ImageSize, List[Automatic, 35]]]], StyleBox[RowBox[List["QuantumMeasurementOperator", " "]], Rule[ShowAutoStyles, False], Rule[ShowStringCharacters, False], Rule[FontSize, Times[0.9`, Inherited]], Rule[FontColor, GrayLevel[0.1`]]]]], Rule[GridBoxSpacings, List[Rule["Columns", List[List[0.25`]]]]]], Rule[Alignment, List[Left, Baseline]], Rule[BaselinePosition, Baseline], Rule[FrameMargins, List[List[3, 0], List[0, 0]]], Rule[BaseStyle, List[Rule[LineSpacing, List[0, 0]], Rule[LineBreakWithin, False]]]], RowBox[List["PacletSymbol", "[", RowBox[List["\"Wolfram/QuantumFramework\"", ",", "\"QuantumMeasurementOperator\""]], "]"]], Rule[TooltipStyle, List[Rule[ShowAutoStyles, True], Rule[ShowStringCharacters, True]]]], Function[Annotation[Slot[1], Style[Defer[PacletSymbol["Wolfram/QuantumFramework", "QuantumMeasurementOperator"]], Rule[ShowStringCharacters, True]], "Tooltip"]]], Rule[Background, RGBColor[0.968`, 0.976`, 0.984`]], Rule[BaselinePosition, Baseline], Rule[DefaultBaseStyle, List[]], Rule[FrameMargins, List[List[0, 0], List[1, 1]]], Rule[FrameStyle, RGBColor[0.831`, 0.847`, 0.85`]], Rule[RoundingRadius, 4]], PacletSymbol["Wolfram/QuantumFramework", "QuantumMeasurementOperator"], Rule[Selectable, False], Rule[SelectWithContents, True], Rule[BoxID, "PacletSymbolBox"]][bobBase][
aliceQubit][
"SimulatedMeasurement"] /. {Wolfram`QuantumFramework`QuditName[
Subscript["\[Psi]",
Subscript["z", "+"]], "Dual" -> False] | Wolfram`QuantumFramework`QuditName[
Subscript["\[Psi]",
Subscript["x", "+"]], "Dual" -> False] :> 0, Wolfram`QuantumFramework`QuditName[
Subscript["\[Psi]",
Subscript["z", "-"]], "Dual" -> False] | Wolfram`QuantumFramework`QuditName[
Subscript["\[Psi]",
Subscript["x", "-"]], "Dual" -> False] :> 1};
If[aliceBase == bobBase, {Append[x, aliceBit], Append[y, bobBit]}, {x, y}]]](https://www.wolframcloud.com/obj/resourcesystem/images/b7a/b7acdc31-f5bd-43d2-a50f-580e75215231/1-0-19/30718d7133553b25.png)