Get a pure function whose argument is a matrix for a given tensor
Contributed by:
E. Chan-López & Víctor Castellanos
Examples
Basic Examples (3)
Define a function that takes a matrix of variables as input and returns a vector:
Apply the function:
Use TensorPureFunction with a tensor of rank 3:
Apply the function:
Use TensorPureFunction with a tensor of rank 4:
Apply the function:
Scope (3)
Use TensorPureFunction in combination with Grad:
Use TensorPureFunction in combination with Curl:
Use TensorPureFunction to compute a Jacobian matrix:
Apply the Jacobian function:
Use TensorPureFunction to compute a Hessian matrix:
Apply the Hessian function:
Applications (4)
Multilinear Functions (2)
Use TensorPureFunction with the following trilinear function:
Apply the trilinear function:
Deformation Gradient and Vorticity Tensor (2)
Define a simple function to compute the deformation gradient given a velocity field at the point :
The calculation of the deformation gradient for the -velocity is as follows:
Now, use TensorPureFunction to obtain a pure function of the above array:
Define a simple function to compute the vorticity tensor given a velocity field at the point :
The calculation of the vorticity tensor for the -velocity is as follows:
Now, use TensorPureFunction to obtain a pure function of the above array:
Properties and Relations (3)
Use TensorPureFunction with the resource function JacobianMatrix:
This is equivalent the computing the Jacobian directly:
Use TensorPureFunction with the resource function HessianMatrix:
This is equivalent the computing the Hessian directly:
Use TensorPureFunction with the resource function DVectorField:
The previous tensors are identical, as seen below:
Publisher
Ramón Eduardo Chan López
Version History
-
2.1.1
– 26 March 2025
-
2.1.0
– 19 February 2025
-
2.0.1
– 20 March 2024
-
2.0.0
– 02 October 2023
-
1.0.0
– 08 November 2022
Related Resources
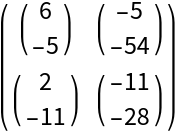
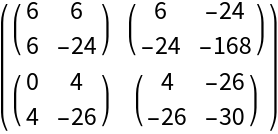
![d3 = ResourceFunction["TensorPureFunction", ResourceVersion->"2.0.0"][{-2 x3 y1 y2 - 2 x2 y1 y3 - 2 x1 y2 y3, 4 x2 x3 y1 + 4 x1 x3 y2 + 4 x1 x2 y3}, {{x1, y1}, {x2, y2}, {x3, y3}}]](https://www.wolframcloud.com/obj/resourcesystem/images/169/1691b320-b7c2-450f-a089-fc775ad1c045/2-0-0/017507588635f1d7.png)
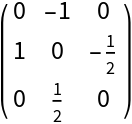
![ResourceFunction["TensorPureFunction"][
Simplify@
ResourceFunction["JacobianMatrix"][{x^3 - 2 x y - y^6, x y^2 - 5 x y}, {x, y}], {{x, y}}]](https://www.wolframcloud.com/obj/resourcesystem/images/169/1691b320-b7c2-450f-a089-fc775ad1c045/2-0-0/14433f156eec870e.png)
![d21 = ResourceFunction["TensorPureFunction"][
DVectorField[{x - y^2, 2 y/x}, {x, y}, {1, 2}, 2, "MultilinearFunction"], {{x1, y1}, {x2, y2}}];](https://www.wolframcloud.com/obj/resourcesystem/images/169/1691b320-b7c2-450f-a089-fc775ad1c045/2-0-0/38c70ea8936c2d13.png)