Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Warning: This resource is provisional

Function Repository Resource:

 SampleUnivariateFunctions (1.1.0) current version: 1.2.1 »

Source Notebook

Get one or more random functions of a single complex variable

Contributed by: Paco Jain

ResourceFunction["SampleUnivariateFunctions"][]

returns a random univariate function in terms of the complex variable z, and possibly one or more parameters.

ResourceFunction["SampleUnivariateFunctions"][All]

returns all available functions.

Details and Options

ResourceFunction["SampleUnivariateFunctions"] takes the following options:
"IncludedSubexpressions"{}all of the supplied forms must appear as subexpressions of the returned function(s)
"ExcludedSubexpressions"{}none of the supplied forms may appear as subexpressions of the returned function(s)
By default, ResourceFunction["SampleUnivariateFunctions"] returns expressions wrapped in Hold, each written in terms of the independent variable z (FormalZ) and zero or more other formal symbols representing unspecified parameters. Domains in z are presumed to be the entire complex plane, but extra parameters may have additional restrictions. It is up to the user to pick suitable values for these extra parameters.

Examples

Basic Examples (2) 

Get some arbitrary sample functions:

In[1]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[1]=
In[2]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[2]=
In[3]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[3]=
In[4]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[4]=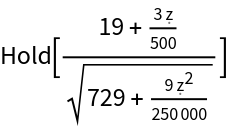

Get a random sample of five univariate functions:

In[5]:=
RandomSample[funcs, 5]
Out[5]=

Scope (2) 

To get all available functions, use the argument All:

In[6]:=
funcs = ResourceFunction["SampleUnivariateFunctions"][All]; Length[funcs]
Out[7]=

Besides the independent variable z, functions may contain unspecified parameters in the "Global`" context (here, a, b, c and d):

In[8]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[8]=

Options (5) 

IncludedSubexpressions (3) 

Get a single function containing BesselJ as a subexpression:

In[9]:=
ResourceFunction["SampleUnivariateFunctions"][ "IncludedSubexpressions" -> {BesselJ}]
Out[9]=

Get all sample functions containing BesselJ as a subexpression and get a count of the number available:

In[10]:=
besselJFuncs = ResourceFunction["SampleUnivariateFunctions"][All, "IncludedSubexpressions" -> {BesselJ}]; Length[besselJFuncs]
Out[11]=

View a subset of these functions:

In[12]:=
RandomSample[besselJFuncs, 5]
Out[12]=

ExcludedSubexpressions (2) 

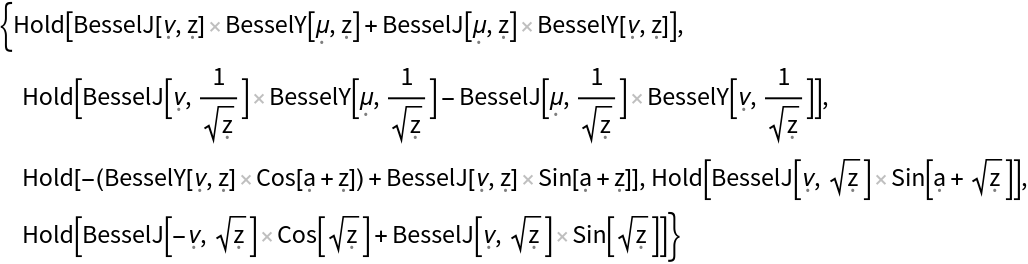Get all sample functions containing BesselJ, but excluding Hypergeometric0F1Regularized and Sum:

In[13]:=
mySample = ResourceFunction["SampleUnivariateFunctions"][All, "IncludedSubexpressions" -> {BesselJ}, "ExcludedSubexpressions" -> {Hypergeometric0F1Regularized, Sum}];

Get a count of the number of such functions:

In[14]:=
Length[mySample]
Out[14]=

Properties and Relations (1) 

Use SeedRandom to get a repeatable sequence of functions:

In[15]:=
SeedRandom[2345]; ResourceFunction["SampleUnivariateFunctions"][]
Out[16]=
In[17]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[17]=
In[18]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[18]=

Publisher

Wolfram|Alpha Math Team

Version History

  • 1.2.1 – 17 January 2023
  • 1.2.0 – 10 January 2023
  • 1.1.0 – 13 December 2022
  • 1.0.0 – 29 November 2022

Related Resources

License Information