Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Warning: This resource is provisional

Function Repository Resource:

 SampleUnivariateFunctions (1.0.0) current version: 1.2.1 »

Source Notebook

Get one or more random functions of a single complex variable

Contributed by: Paco Jain

ResourceFunction["SampleUnivariateFunctions"][]

returns a random univariate function in terms of the complex variable z, and possibly one or more parameters.

ResourceFunction["SampleUnivariateFunctions"][All]

returns all available functions.

Details and Options

ResourceFunction["SampleUnivariateFunctions"] returns functions written in terms of the Global` variable z.
ResourceFunction["SampleUnivariateFunctions"] takes the following options:
"IncludedSubexpressions"{_}all of the supplied forms must appear as subexpressions of the returned function(s)
"ExcludedSubexpressions"{}none of the supplied forms may appear as subexpressions of the returned function(s)

Examples

Basic Examples (3) 

Get some arbitrary sample functions:

In[1]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[1]=
In[2]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[2]=
In[3]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[3]=
In[4]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[4]=

Besides the independent variable z, functions may contain unspecified parameters in the "Global`" context (here, A, B, b, and c):

In[5]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[5]=

To get all available functions, use the argument All:

In[6]:=
funcs = ResourceFunction["SampleUnivariateFunctions"][All]; Length[funcs]
Out[7]=

Get a random sample of five univariate functions:

In[8]:=
RandomSample[funcs, 5]
Out[8]=

Options (5) 

IncludedSubexpressions (3) 

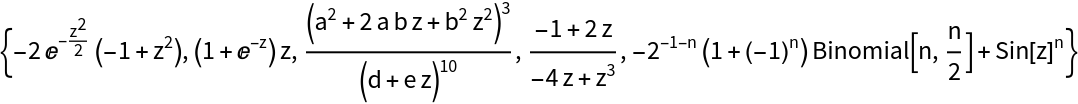Get a single function containing BesselJ as a subexpression:

In[9]:=
ResourceFunction["SampleUnivariateFunctions"][ "IncludedSubexpressions" -> {BesselJ}]
Out[9]=

Get all sample functions containing BesselJ as a subexpression and get a count of the number available:

In[10]:=
besselJFuncs = ResourceFunction["SampleUnivariateFunctions"][All, "IncludedSubexpressions" -> {BesselJ}]; Length[besselJFuncs]
Out[11]=

View a subset of these functions:

In[12]:=
RandomSample[besselJFuncs, 5]
Out[12]=

ExcludedSubexpressions (2) 

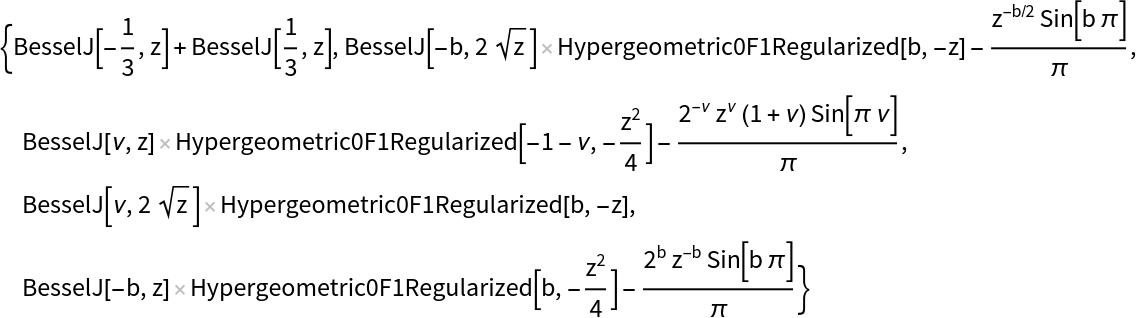Get all sample functions containing BesselJ, but excluding Hypergeometric0F1Regularized and Sum:

In[13]:=
mySample = ResourceFunction["SampleUnivariateFunctions"][All, "IncludedSubexpressions" -> {BesselJ}, "ExcludedSubexpressions" -> {Hypergeometric0F1Regularized, Sum}];

Get a count of the number of such functions:

In[14]:=
Length[mySample]
Out[14]=

Properties and Relations (1) 

Use SeedRandom to get a repeatable sequence of functions:

In[15]:=
SeedRandom[1234]; ResourceFunction["SampleUnivariateFunctions"][]
Out[16]=
In[17]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[17]=
In[18]:=
ResourceFunction["SampleUnivariateFunctions"][]
Out[18]=

Publisher

Wolfram|Alpha Math Team

Version History

  • 1.2.1 – 17 January 2023
  • 1.2.0 – 10 January 2023
  • 1.1.0 – 13 December 2022
  • 1.0.0 – 29 November 2022

Related Resources

License Information