IncludedSubexpressions (3)
Get a single function containing BesselJ as a subexpression:
Get all sample functions containing BesselJ as a subexpression and count the number available:
View a subset of five of these functions:
Every pattern listed in the value for "IncludedSubexpressions" must be separately included in the result. As such, additional forms in the list value of "IncludedSubexpressions" always reduce (or leave unchanged) the numbers of results:
The second sample is a subset of the first:
To form a more inclusive pattern, allowing either BesselJ or BesselK, instead use Alternatives:
OutputForm (4)
Results can be returned in one of several forms, as determined by the "OutputForm" option. The setting "OutputForm"→Automatic (the default) returns bare expressions, written in terms of formal symbols:
For ease in substituting user-supplied parameter/variable values, the setting "OutputType"→"PureFunction" can be useful (note that the independent variable, z, always appears as the first argument of the returned Function expressions):
On supplying values, Function ignores extra parameters, using only the number needed to fill its slots:
The setting "OutputType"→"NestedFunction" separates the independent variable (z) from other parameters using separate Function wrappers:
The setting "OutputForm"→ "Held" causes results to be returned wrapped in Hold:
The setting "OutputForm"→"PureFunction" can be preferable for certain calculations (e.g., using Derivative, Plot, …):
Using "OutputForm"→ "Held" can result in quicker returns for large batches of functions (e.g., All), as each expression is shielded from kernel evaluation:
Auto-evaluation can cause some functions to change form, hiding the inclusion of certain subexpressions:
Though we requested a function containing Sqrt as a subexpression, it is absent in the result:
By viewing the FullForm, we see that what the front end renders as  is actually Power[#,Rational[1,2]& at the expression level:
is actually Power[#,Rational[1,2]& at the expression level:
Using "OutputForm"→ "Held" preserves the "original" form of expressions, prior to kernel evaluation:
We now see the Sqrt we expect in the expression's FullForm:
TrueUnivariate (3)
To get functions free of any symbolic parameters besides the independent variable z, use the option setting "TrueUnivariate"→True:
The setting "TrueUnivariate"→ False returns only functions that do contain extra parameters:
The default setting "TrueUnivariate" → Automatic returns a mix of functions that do and do not contain extra parameters:
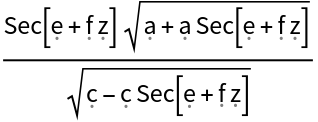
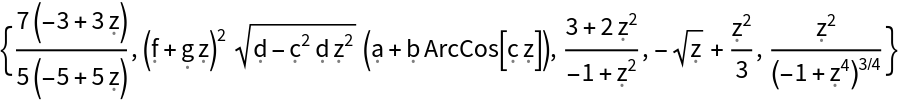
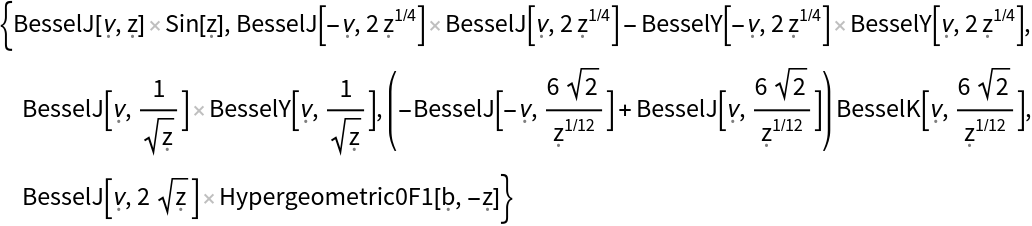
![mySample = ResourceFunction["SampleUnivariateFunctions"][All, "IncludedSubexpressions" -> {BesselJ}, "ExcludedSubexpressions" -> {Hypergeometric0F1Regularized, Sum}];](https://www.wolframcloud.com/obj/resourcesystem/images/412/41220d47-7955-41fb-b2af-fc0961b361ca/4949139bae1ff4c1.png)
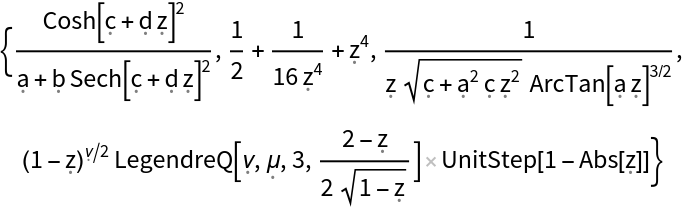
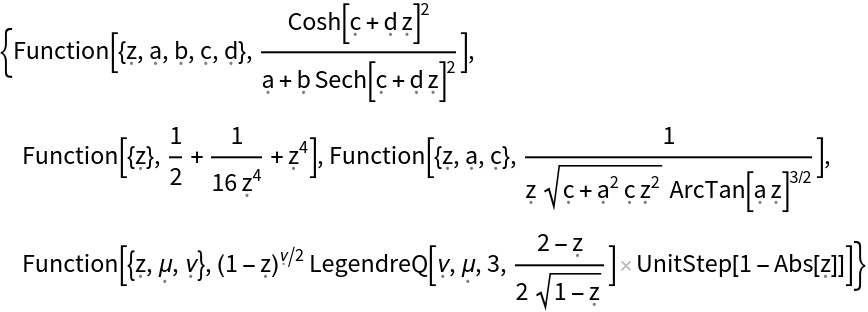
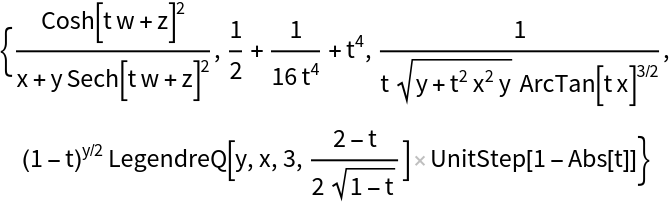
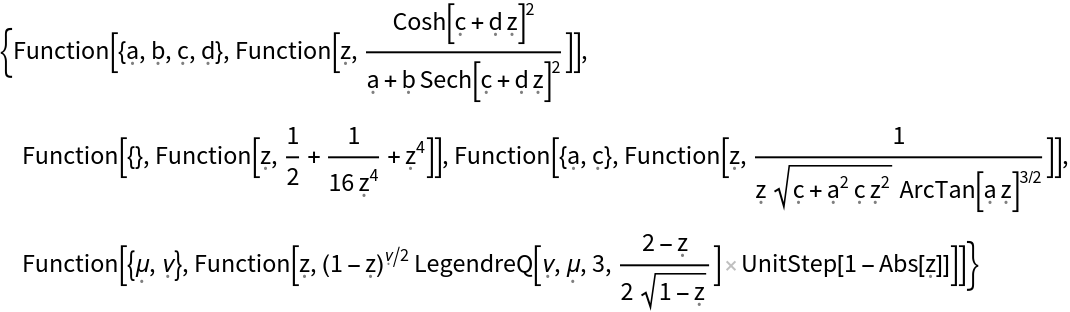
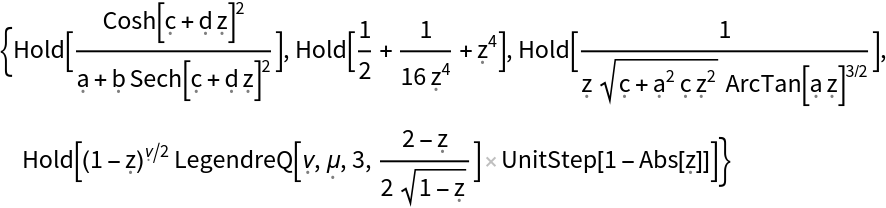
![]() is actually Power[#,Rational[1,2]& at the expression level:
is actually Power[#,Rational[1,2]& at the expression level:![SeedRandom[2];
myHeldFunc = ResourceFunction["SampleUnivariateFunctions"][
"IncludedSubexpressions" -> {Sqrt}, "OutputForm" -> "Held"]](https://www.wolframcloud.com/obj/resourcesystem/images/412/41220d47-7955-41fb-b2af-fc0961b361ca/4aad06a78df65a19.png)
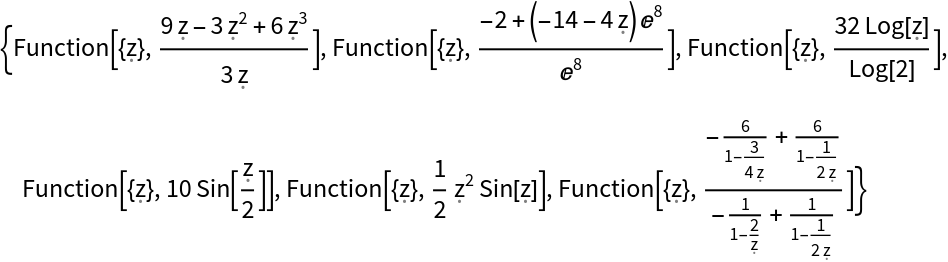
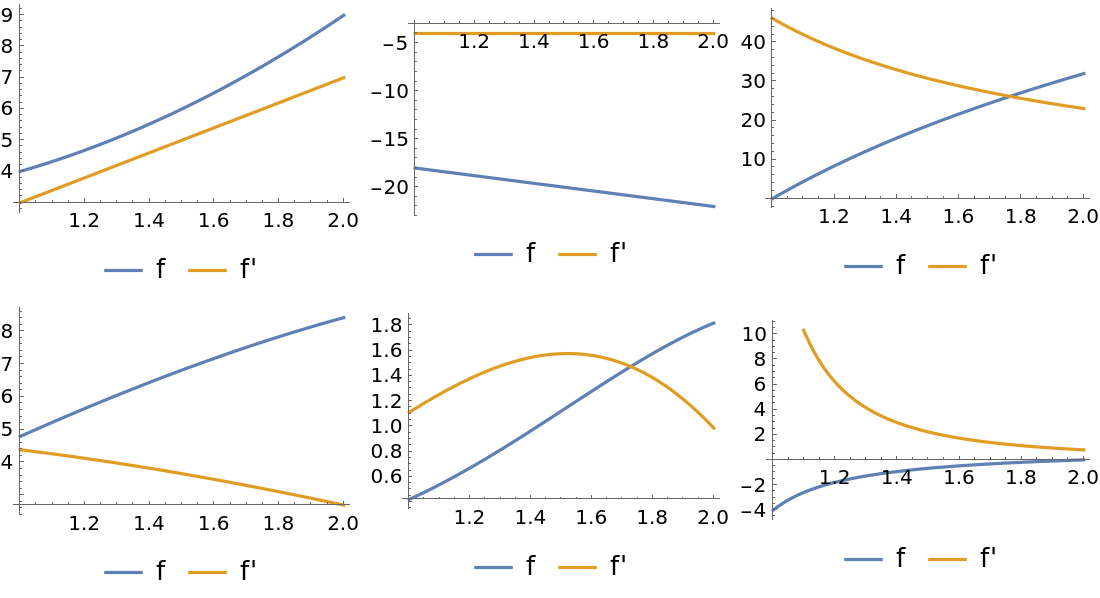
![funcArray = Partition[funcList, 3];
Grid@MapAt[
Plot[{#[x], Derivative[1][#][x]}, {x, 1, 2}, PlotLegends -> Placed[{"f", "f'"}, Below]] &, funcArray, {All, All}]](https://www.wolframcloud.com/obj/resourcesystem/images/412/41220d47-7955-41fb-b2af-fc0961b361ca/2687d7c7bfb2d863.png)