Function Repository Resource:

ArgHue

Source Notebook

Map the argument of a complex number to a color

Contributed by: Ted Ersek

ResourceFunction["ArgHue"][arg]

returns Hue[h,1,1] where h depends on the value of arg.

ResourceFunction["ArgHue"][arg,abs]

creates a Hue based on the argument arg and magnitude abs of a complex value.

Details and Options

The parameter arg must be a real number.

The parameter abs must be a real number in the closed interval [0,1].

When using ResourceFunction["ArgHue"] as a ColorFunction, the setting ColorFunctionScaling→False should also be used.

ArgHue takes the following option:

ZeroColor

White

approach this color as the parameter abs approaches zero

The setting of the ZeroColor option can be any color.

Examples

Basic Examples (2)

When arg is a real number, ArgHue[arg] returns a hue with full saturation and full brightness:

In[1]:=

$colors = Table[ResourceFunction["ArgHue"][arg], {arg, -\[Pi], \[Pi], \[Pi]/4}]$

Out[1]=

Display the above colors in a way that indicates the direction in the complex plane they represent:

In[2]:=

$Graphics[ Flatten[{Transpose@{colors, Table[Disk[{0, 0}, 1, {\[Theta] - \[Pi]/50, \[Theta] + \[Pi]/ 50}], {\[Theta], -\[Pi], \[Pi], \[Pi]/4}]}, White, Disk[{0, 0}, 0.5], Black, Line[{{-0.5, 0}, {0.5, 0}}], Line[{{0, -0.5}, {0, 0.5}}]}]]$

Out[2]=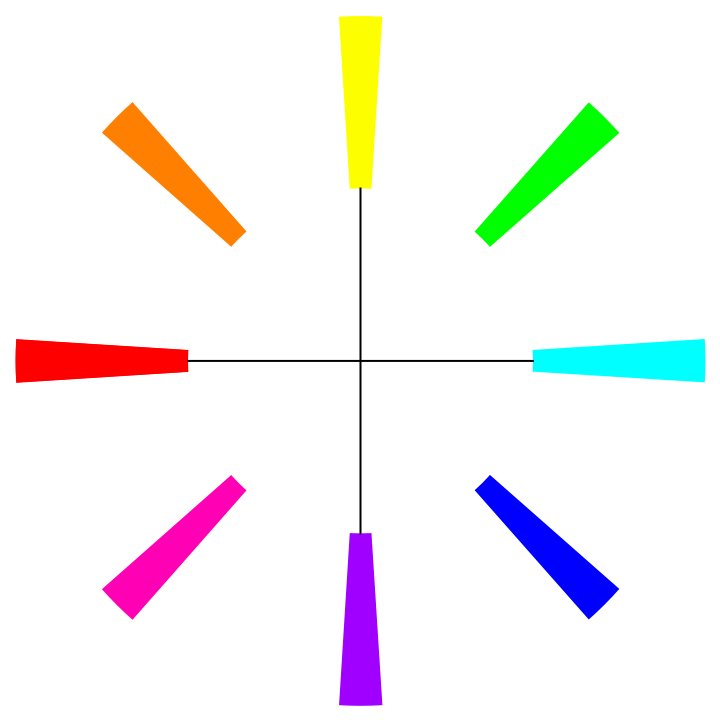

Make a color wheel around the origin of the complex plane:

In[3]:=

$Graphics[ Flatten@{Table[{ResourceFunction["ArgHue"][arg], Disk[{0, 0}, 1, {arg - \[Pi]/400, arg + \[Pi]/400}]}, {arg, -\[Pi], \[Pi], \[Pi]/210}], White, Disk[{0, 0}, 0.7]}, Axes -> True, AxesLabel -> {"Re", "Im"}, Ticks -> None]$

Out[3]=

Options (5)

ZeroColor (5)

When the ZeroColor setting is White, ArgHue[arg,abs] returns a color that approaches White as abs approaches 0:

In[4]:=

$SetOptions[ResourceFunction["ArgHue"], ZeroColor -> White]; Table[ResourceFunction["ArgHue"][arg, abs], {abs, {0.15, 0.3, 0.6, 1}}, {arg, -\[Pi], \[Pi], \[Pi]/ 8}] // TableForm$

Out[5]=

When the ZeroColor setting is Black, ArgHue[arg,abs] returns a color that approaches Black as abs approaches 0:

In[6]:=

$SetOptions[ResourceFunction["ArgHue"], ZeroColor -> Black]; Table[ResourceFunction["ArgHue"][arg, abs], {abs, {0.55, 0.65, 0.8, 1}}, {arg, -\[Pi], \[Pi], \[Pi]/ 8}] // TableForm$

Out[7]=

Specify that White should be used where the function approaches zero:

In[8]:=

SetOptions[ResourceFunction["ArgHue"], ZeroColor -> White];
ComplexPlot[z, {z, -1 - I, 1 + I}, ColorFunction -> {Function[{re, im, abs, arg}, ResourceFunction["ArgHue"][arg, abs]], None}, ColorFunctionScaling -> False]

Out[9]=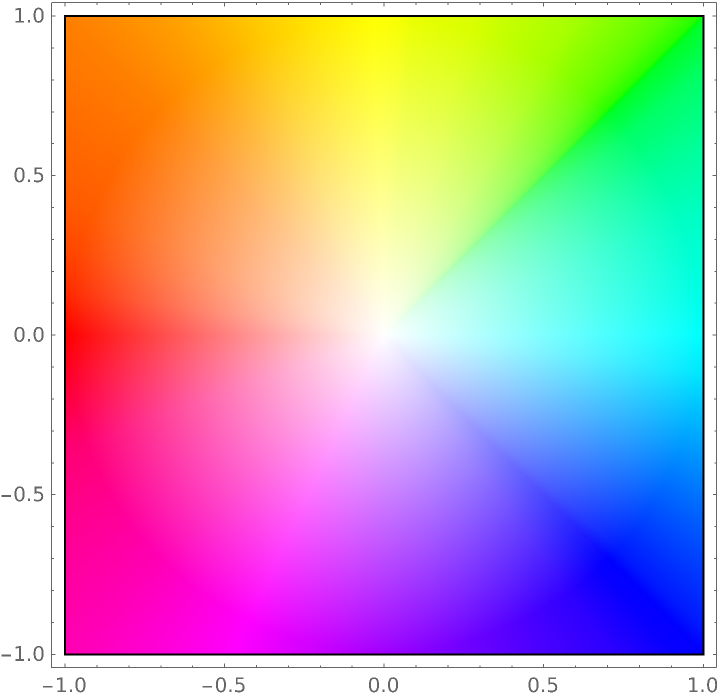

Specify that GrayLevel[0.4] should be used where the function approaches zero:

In[10]:=

SetOptions[ResourceFunction["ArgHue"], ZeroColor -> GrayLevel[0.4]];
ComplexPlot[z, {z, -1 - I, 1 + I}, ColorFunction -> {Function[{re, im, abs, arg}, ResourceFunction["ArgHue"][arg, abs]], None}, ColorFunctionScaling -> False]

Out[11]=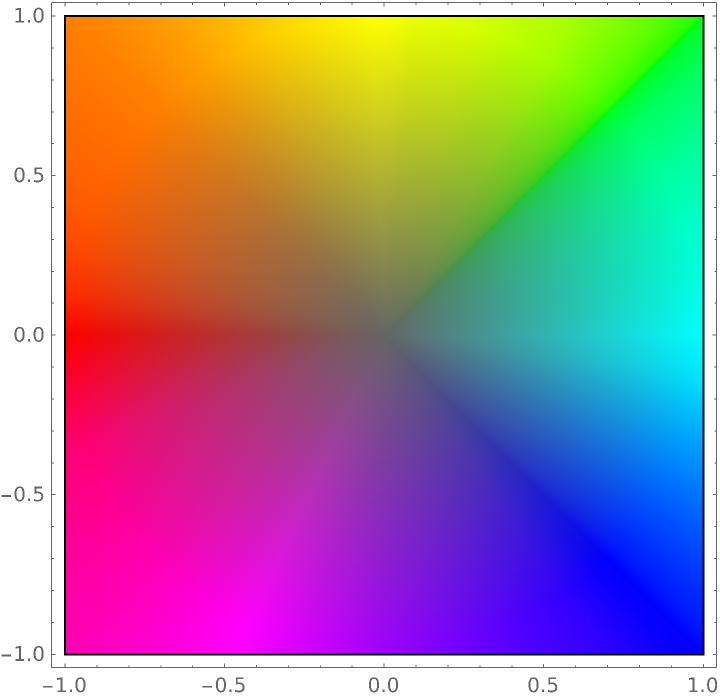

Specify that RGBColor[1,0.8,0.8] should be used where the function approaches zero:

In[12]:=

ComplexPlot[z, {z, -1 - I, 1 + I}, ColorFunction -> {Function[{re, im, abs, arg}, ResourceFunction["ArgHue"][arg, abs, ZeroColor -> RGBColor[1, 0.8, 0.8]]], None}, ColorFunctionScaling -> False]

Out[12]=

Applications (13)

AbsArgPlot (1)

Use ArgHue in the ColorFunction setting of AbsArgPlot:

In[13]:=

$AbsArgPlot[Abs[\[Theta]] Exp[I \[Theta]], {\[Theta], -\[Pi], \[Pi]}, ColorFunction -> ResourceFunction["ArgHue"], ColorFunctionScaling -> False, PlotStyle -> AbsoluteThickness[8]]$

Out[13]=

ComplexPlot (3)

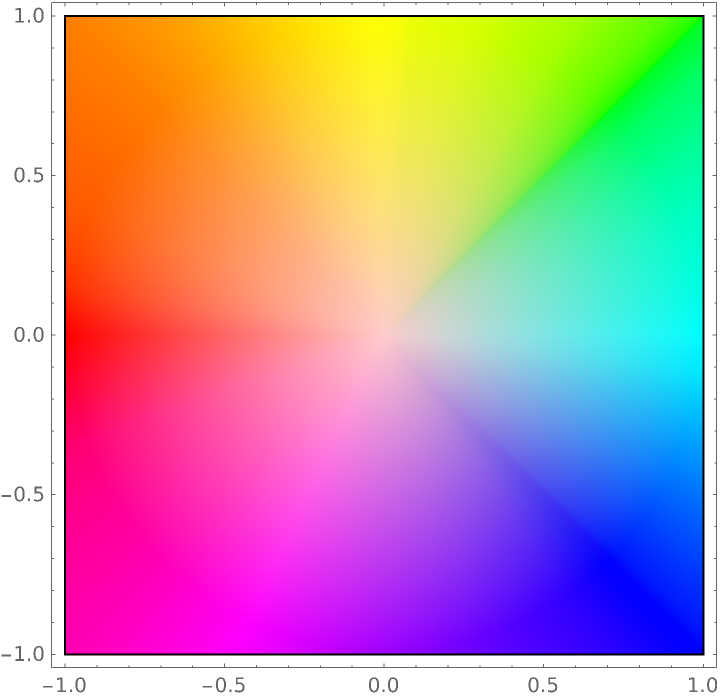Use ArgHue in the ColorFunction setting of ComplexPlot with the hue indicating the argument of the function value:

In[14]:=

ComplexPlot[z, {z, -1 - I, 1 + I}, ColorFunction -> {Function[{re, im, abs, arg}, ResourceFunction["ArgHue"][arg]], None}, ColorFunctionScaling -> False, Exclusions -> None]

Out[14]=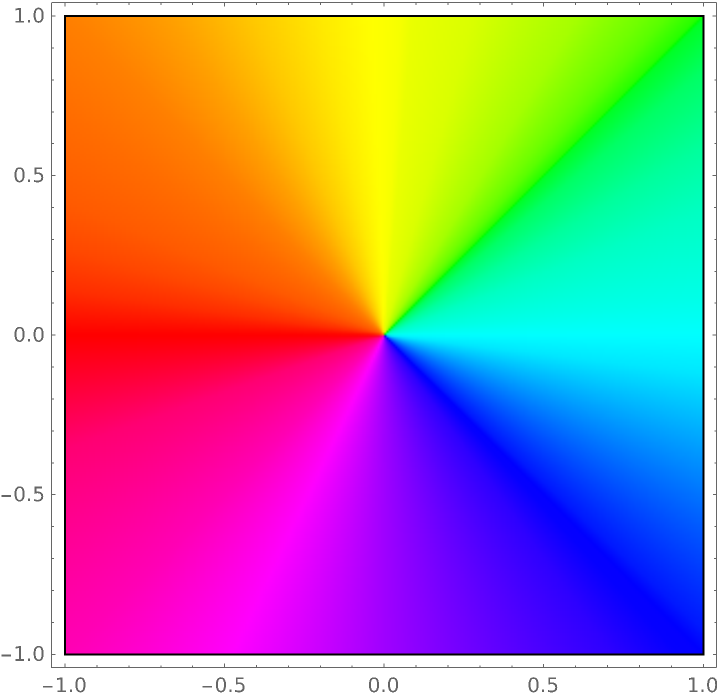

Use ArgHue in the ColorFunction setting of ComplexPlot with the hue indicating the argument of the function value and a color that approaches White as the function value approaches zero:

In[15]:=

Out[16]=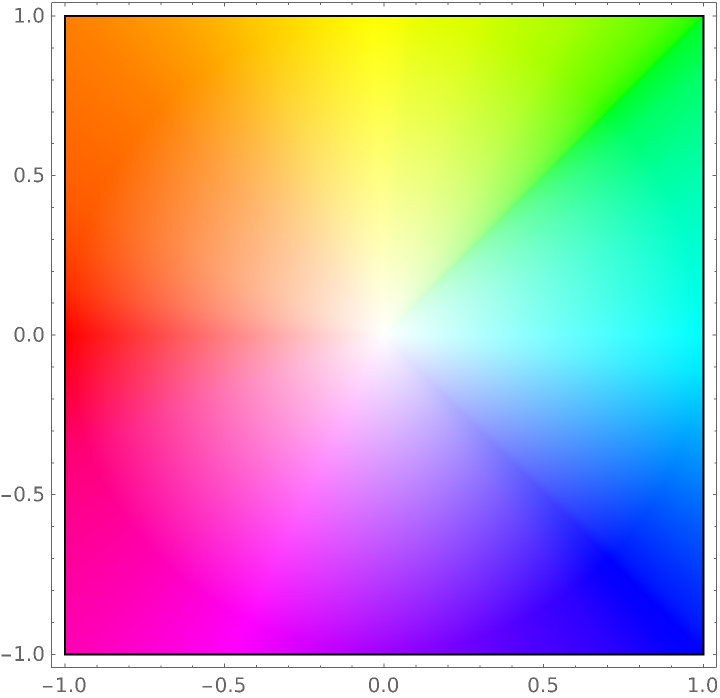

Use ArgHue in the ColorFunction setting of ComplexPlot with the hue indicating the argument of the function value and a color that approaches Black as the function value approaches zero:

In[17]:=

SetOptions[ResourceFunction["ArgHue"], "ZeroColor" -> Black];
ComplexPlot[z, {z, -1 - I, 1 + I}, ColorFunction -> {Function[{re, im, abs, arg}, ResourceFunction["ArgHue"][arg, abs]], None}, ColorFunctionScaling -> False]

Out[18]=

ComplexPlot3D (3)

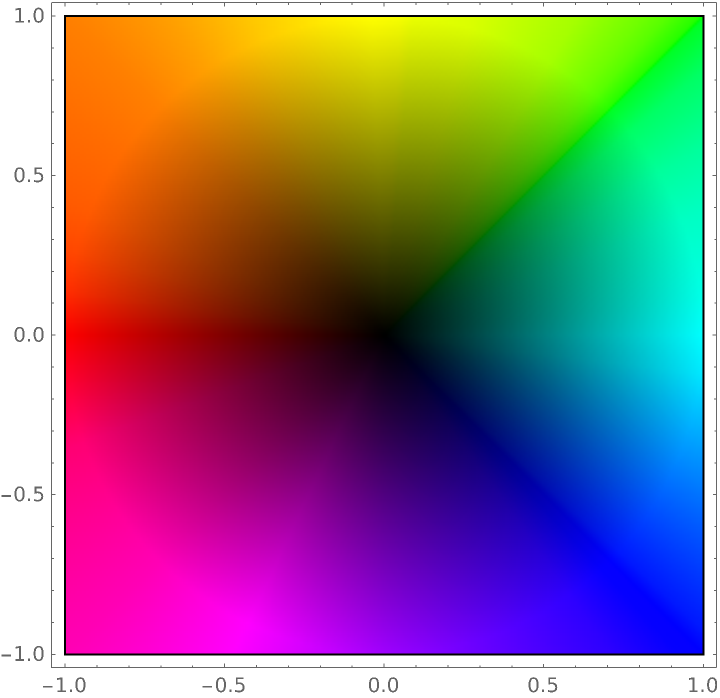Use ArgHue in the ColorFunction setting of ComplexPlot3D with the hue indicating the argument of the function value:

In[19]:=

Out[19]=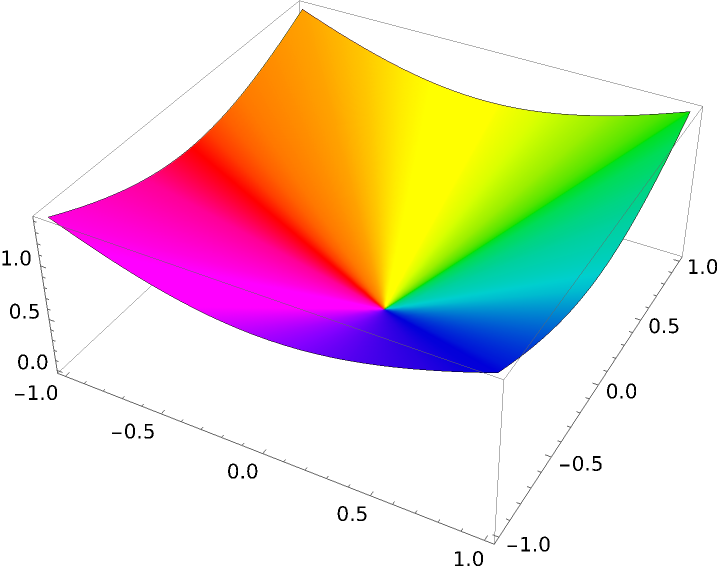

Use ArgHue in the ColorFunction setting of ComplexPlot3D with the hue indicating the argument of the function value and a color that approaches White as the function value approaches zero:

In[20]:=

SetOptions[ResourceFunction["ArgHue"], "ZeroColor" -> White];
ComplexPlot3D[z, {z, -1 - I, 1 + I}, ColorFunction -> Function[{re, im, abs, arg}, ResourceFunction["ArgHue"][arg, abs]], ColorFunctionScaling -> False, Exclusions -> None]

Out[21]=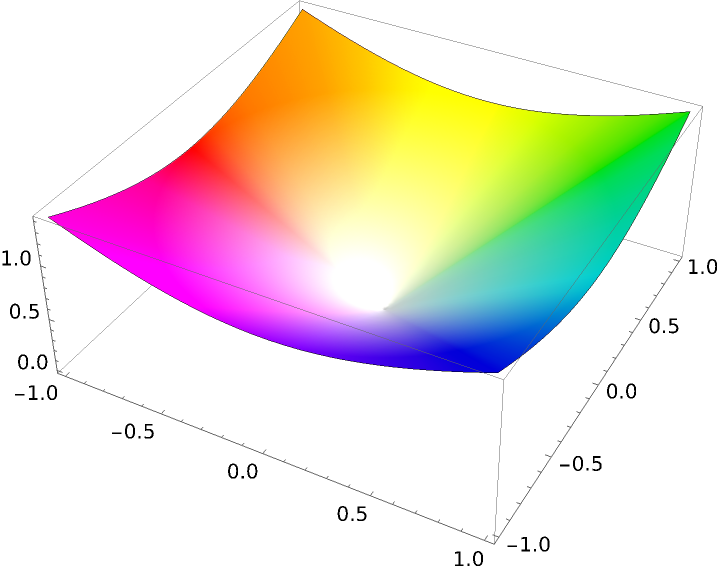

Use ArgHue in the ColorFunction setting of ComplexPlot3D with the hue indicating the argument of the function value and a color that approaches Black as the function value approaches zero:

In[22]:=

SetOptions[ResourceFunction["ArgHue"], "ZeroColor" -> Black];
ComplexPlot3D[z, {z, -1 - I, 1 + I}, ColorFunction -> Function[{re, im, abs, arg}, ResourceFunction["ArgHue"][arg, abs]], ColorFunctionScaling -> False, Exclusions -> None]

Out[23]=

ComplexListPlot (3)

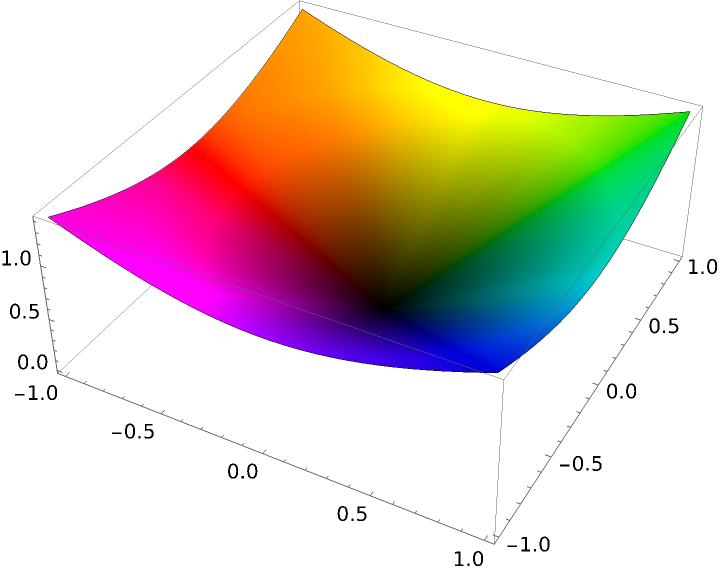Use ArgHue in the ColorFunction setting of ComplexListPlot with the hue indicating the argument of the function value:

In[24]:=

$pnts = Table[(1 + \[Theta]) E^(I \[Theta]), {\[Theta], \[Pi]/36, 6 \[Pi], \[Pi]/18}]; ComplexListPlot[pnts, PlotStyle -> AbsolutePointSize[7], ColorFunction -> Function[{re, im, arg, abs}, ResourceFunction["ArgHue"][arg]], ColorFunctionScaling -> False]$

Out[25]=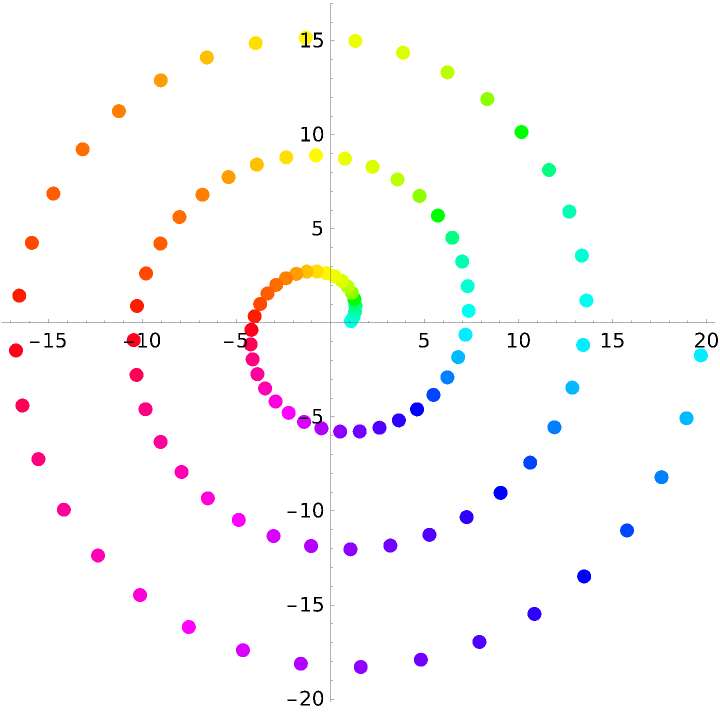

Use ArgHue in the ColorFunction setting of ComplexListPlot with the hue indicating the argument of the function value and a color that approaches White as the function value approaches zero:

In[26]:=

$SetOptions[ResourceFunction["ArgHue"], "ZeroColor" -> White]; ComplexListPlot[ Table[(1 + \[Theta]) E^(I \[Theta]), {\[Theta], \[Pi]/36, 6 \[Pi], \[Pi]/18}], PlotStyle -> AbsolutePointSize[7], ColorFunction -> Function[{re, im, arg, abs}, ResourceFunction["ArgHue"][arg, abs/15]], ColorFunctionScaling -> False]$

Out[3]=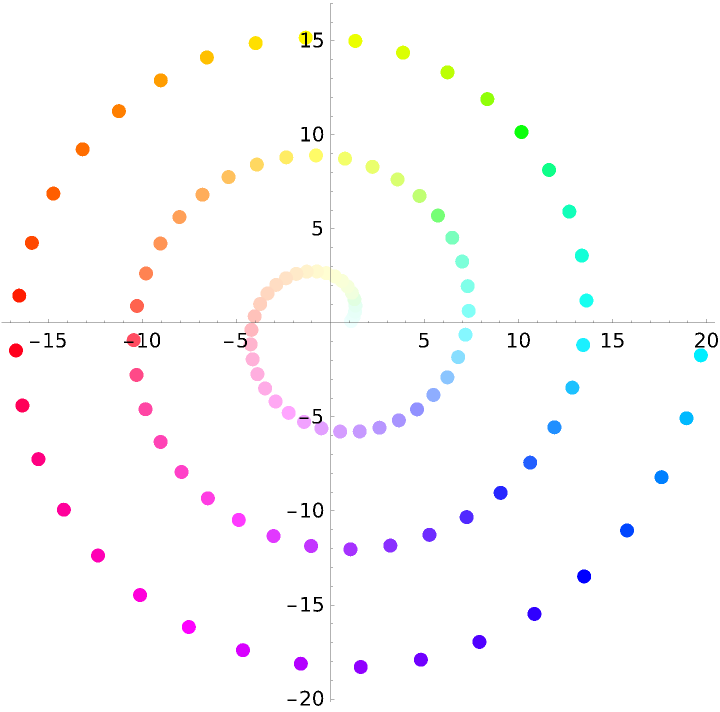

Use ArgHue in the ColorFunction setting of ComplexListPlot with the hue indicating the argument of the function value and a color that approaches Black as the function value approaches zero:

In[27]:=

$SetOptions[ResourceFunction["ArgHue"], "ZeroColor" -> Black]; ComplexListPlot[ Table[(1 + \[Theta]) E^(I \[Theta]), {\[Theta], \[Pi]/36, 6 \[Pi], \[Pi]/18}], PlotStyle -> AbsolutePointSize[7], ColorFunction -> Function[{re, im, arg, abs}, ResourceFunction["ArgHue"][arg, abs/10]], ColorFunctionScaling -> False]$

Out[28]=

ComplexArrayPlot (3)

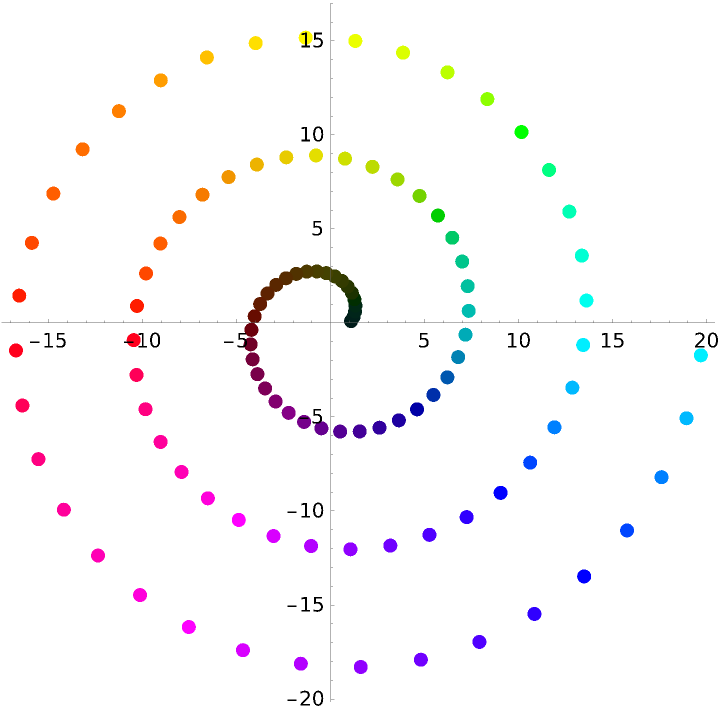Use ArgHue in the ColorFunction setting in ComplexArrayPlot with the hue indicating the argument of the function value:

In[29]:=

$pnts = Table[ Sqrt[x^2 + y^2] E^(-I ArcTan[x, y]), {y, -2, 2.21, 0.42}, {x, -2, 2.1, 0.42}]; ComplexArrayPlot[pnts, ColorFunction -> {Function[{re, im, abs, arg}, ResourceFunction["ArgHue"][arg]], None}, ColorFunctionScaling -> False]$

Out[30]=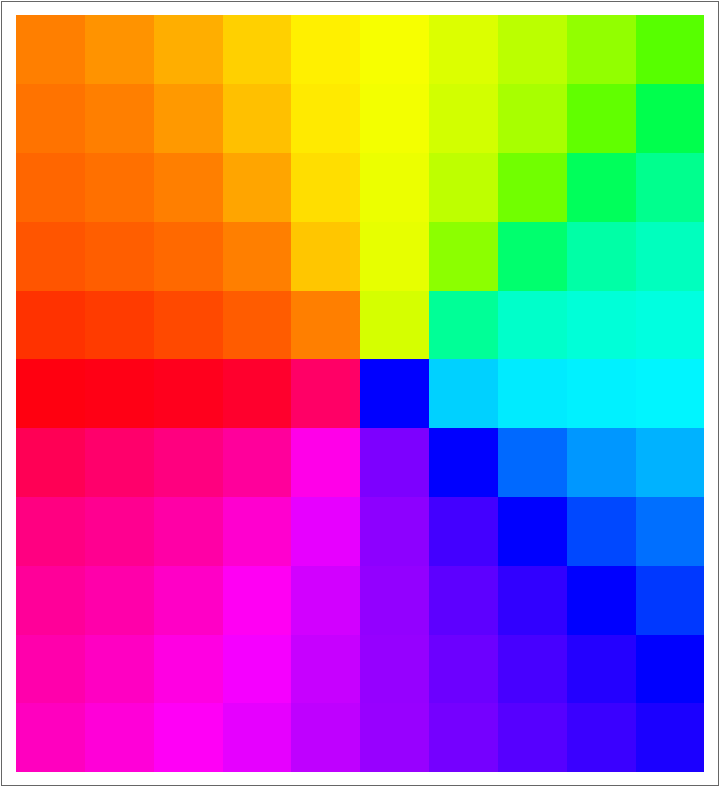

Use ArgHue in the ColorFunction setting of ComplexArrayPlot with the hue indicating the argument of the function value and a color that approaches White as the function value approaches zero:

In[31]:=

$SetOptions[ResourceFunction["ArgHue"], "ZeroColor" -> White]; ComplexArrayPlot[ Table[Sqrt[x^2 + y^2] E^(-I ArcTan[x, y]), {y, -2, 2.21, 0.42}, {x, -2, 2.1, 0.42}], ColorFunction -> {Function[{re, im, abs, arg}, ResourceFunction["ArgHue"][arg, abs/2]], None}, ColorFunctionScaling -> False]$

Out[32]=

Use ArgHue in the ColorFunction setting of ComplexArrayPlot with the hue indicating the argument of the function value and a color that approaches Black as the function value approaches zero:

In[33]:=

$SetOptions[ResourceFunction["ArgHue"], "ZeroColor" -> Black]; ComplexArrayPlot[ Table[Sqrt[x^2 + y^2] E^(-I ArcTan[x, y]), {y, -2, 2.21, 0.42}, {x, -2, 2.1, 0.42}], ColorFunction -> {Function[{re, im, abs, arg}, ResourceFunction["ArgHue"][arg, abs/2]], None}, ColorFunctionScaling -> False]$