Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 LemoineInellipse

Source Notebook

Generate the Lemoine inellipse of a 2D triangle

Contributed by: Jan Mangaldan

ResourceFunction["LemoineInellipse"][{p1,p2,p3}]

returns an Ellipsoid representing the Lemoine inellipse of the triangle defined by vertices p1,p2 and p3.

ResourceFunction["LemoineInellipse"][{p1,p2,p3},property]

gives the value of the specified property.

Details

The Lemoine inellipse of a triangle is the unique ellipse inscribed in a triangle whose foci are the triangle's centroid and Lemoine point.
The following properties are supported:
"Ellipsoid"Ellipsoid representing the inellipse
"Parametric"parametric equation for the inellipse as a pure function
"Implicit"implicit Cartesian equation for the inellipse as a pure function
ResourceFunction["LemoineInellipse"][poly] where poly is a Triangle or Polygon is equivalent to ResourceFunction["LemoineInellipse"][PolygonCoordinates[poly]].

Examples

Basic Examples (1) 

Show a triangle together with its Lemoine inellipse:

In[1]:=
tri = {{0, 0}, {1.2, 4}, {5, 0}}; Graphics[{FaceForm[], {EdgeForm[Red], Triangle[tri]}, {EdgeForm[Blue], ResourceFunction["LemoineInellipse"][tri]}}]
Out[1]=

Scope (5) 

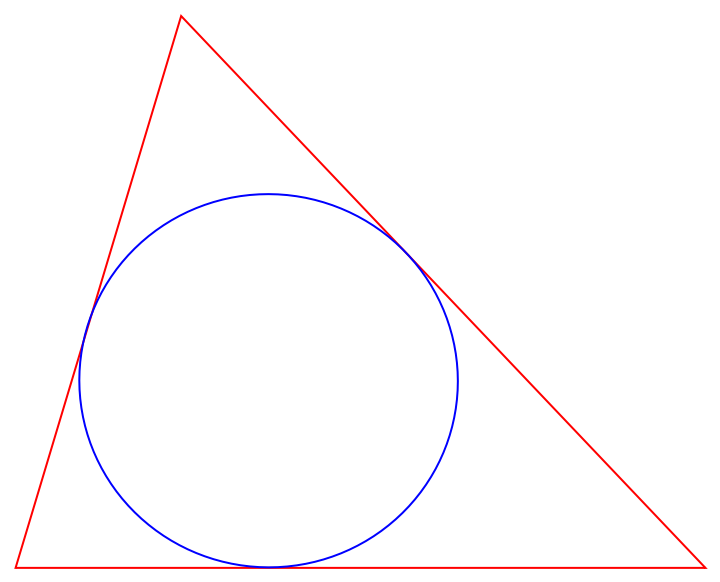A triangle:

In[2]:=
Graphics[tri = Triangle[{{0, 0}, {0.4, 3.1}, {5, 0}}]]
Out[2]=

Generate the parametric equation of the triangle's Lemoine inellipse:

In[3]:=
ell1[t_] = ResourceFunction["LemoineInellipse"][tri, "Parametric"][t]
Out[3]=

Plot the parametric equation along with the triangle:

In[4]:=
Show[Graphics[{FaceForm[], EdgeForm[ColorData[97, 4]], tri}], ParametricPlot[ell1[t], {t, 0, 2 \[Pi]}]]
Out[4]=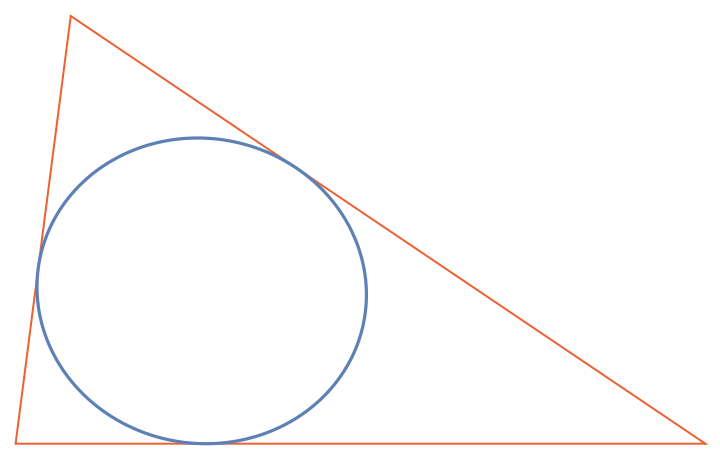

Generate the implicit equation of the triangle's Lemoine inellipse:

In[5]:=
ell2[x_, y_] = ResourceFunction["LemoineInellipse"][tri, "Implicit"][x, y]
Out[5]=

Plot the implicit equation along with the triangle:

In[6]:=
ContourPlot[ell2[x, y] == 0, {x, -1, 6}, {y, -1, 4}, AspectRatio -> Automatic, Epilog -> {FaceForm[], EdgeForm[ColorData[97, 4]], tri}]
Out[6]=

Properties and Relations (2) 

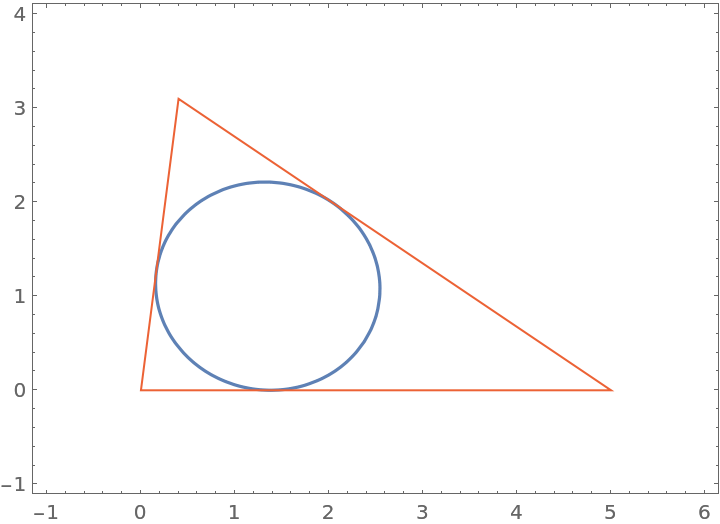Use the resource function EllipseProperties to generate properties of the inellipse:

In[7]:=
tri = {{0, 0}, {1.1, 4}, {5, 0}}; prop = ResourceFunction["EllipseProperties"][ ResourceFunction["LemoineInellipse"][tri, "Implicit"][x, y] == 0, {x, y}]
Out[7]=

Give the foci of the inellipse:

In[8]:=
foc = Lookup[prop, "Foci"]
Out[8]=

One focus corresponds to the centroid:

In[9]:=
TriangleConstruct[tri, "Centroid"] // First // N
Out[9]=

The other focus corresponds to the symmedian point (Lemoine point):

In[10]:=
TriangleConstruct[tri, "SymmedianPoint"] // First // N
Out[10]=

The area of the Lemoine inellipse can be expressed in terms of the area of the original triangle and the lengths of its sides:

In[11]:=
tri = {{0, 0}, {1.5, 4}, {5, 0}}; Area[ResourceFunction["LemoineInellipse"][tri]]
Out[11]=
In[12]:=
sl = SquaredEuclideanDistance @@@ Partition[tri, 2, 1, 1]; ((\[Pi] Sqrt[ 2 SymmetricPolynomial[1, sl] (9 SymmetricPolynomial[2, sl] - 2 SymmetricPolynomial[1, sl]^2) - 27 SymmetricPolynomial[3, sl]])/(3 SymmetricPolynomial[1, sl])^(3/2)) Area[Triangle[tri]]
Out[12]=

Version History

  • 1.0.0 – 13 September 2021

Related Resources

License Information