Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get an Association of the properties of a given ellipse
ResourceFunction["EllipseProperties"][expr,{x,y}] returns an Association of properties of the ellipse defined by expr in terms of the variables x and y. |
Compute the properties of an ellipse:
| In[1]:= |
| Out[1]= |  |
Compute the properties of a ellipse described using other properties:
| In[2]:= |
| Out[2]= |  |
Compute the properties of a skew ellipse (not aligned with the x- or y-axis) described by some properties:
| In[3]:= |
| Out[3]= |  |
| In[4]:= |
| Out[4]= |  |
Compute the properties of a circle as a special case of an ellipse:
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |
Compute the properties of a general ellipse centered at {h,k} with radius semi-axis lengths a and b:
| In[7]:= |
| Out[7]= |  |
Note that we have to give a constraint on a and b in order to fully define the ellipse:
| In[8]:= |
| Out[8]= |  |
Use the resource function InteractiveConicPlot to visualize the results of EllipseProperties:
| In[9]:= |
| Out[9]= | 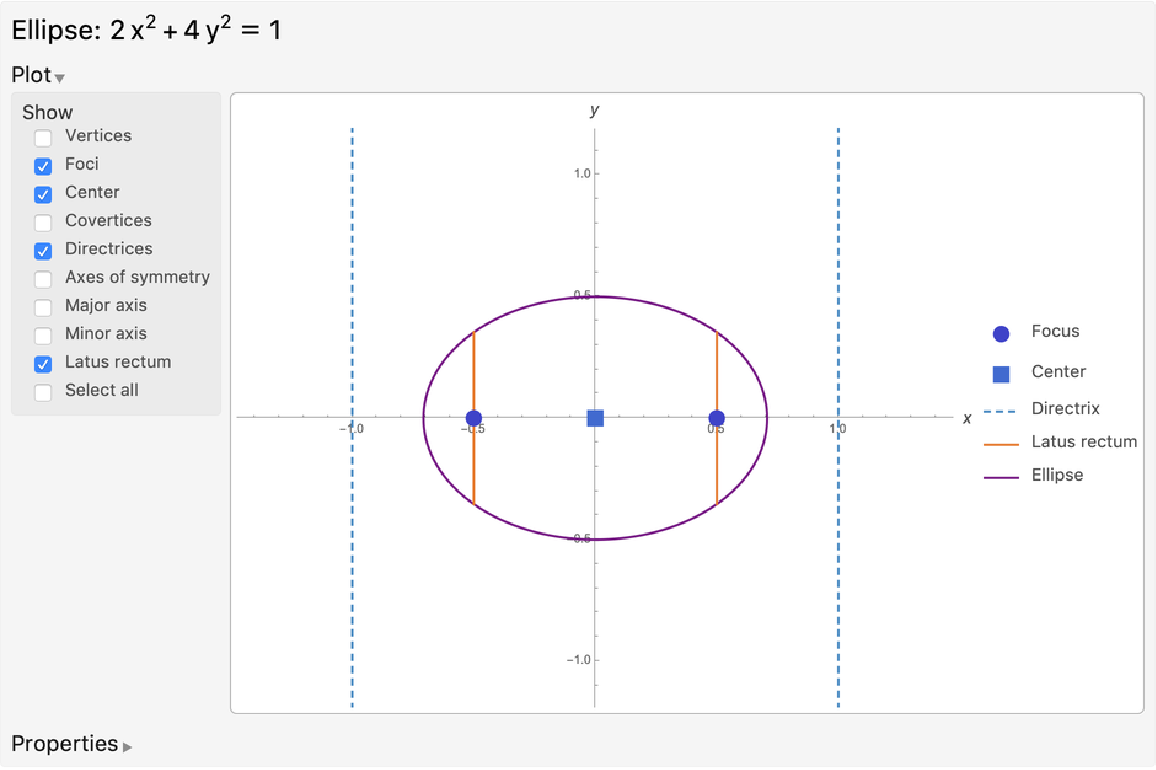 |
If the input equation or Association does not describe an ellipse but describes another conic section, EllipseProperties will return an Association of properties pertaining to the correct conic section, including its "Type" ("Parabola", "Hyperbola" or "Circle"):
| In[10]:= |
| Out[10]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License