Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Return the Gergonne point of a triangle
ResourceFunction["GergonnePoint"][{p1,p2,p3}] returns the Gergonne point of the triangle defined by vertices p1,p2 and p3. |
Find the Gergonne point of three triangle vertices:
| In[1]:= |
| Out[1]= |
The perspectors concur at the Gergonne point (marked Ge in the diagram):
| In[2]:= | ![Graphics[{
{Orange, Opacity[0.2], Triangle[tri]},
TriangleConstruct[tri, "Incircle"],
HalfLine[{tri[[1]], ge[[1]]}],
HalfLine[{tri[[2]], ge[[1]]}],
HalfLine[{tri[[3]], ge[[1]]}],
{
PointSize[
Scaled[0.08]],
Hue[0.58, 1, 1], ge,
Text[
Style["Ge", White, FontSize -> Scaled[0.04]],
Part[ge, 1]]}
}, PlotRange -> {{0, 5}, {-1/3, 4}}]](https://www.wolframcloud.com/obj/resourcesystem/images/633/63365a9b-5f50-4cf7-aa9d-b21b97a271e6/4ba6634b87b777c2.png) |
| Out[2]= | 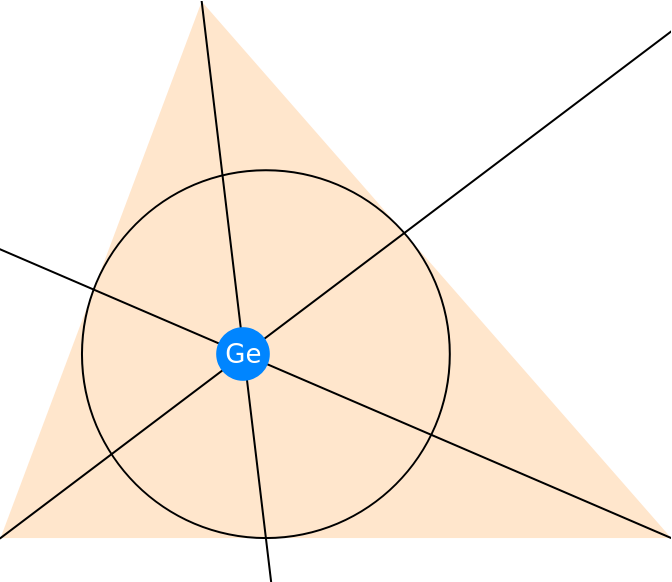 |
Compute the Gergonne point of a 3D triangle:
| In[3]:= |
| Out[3]= |
Show the Gergonne point and the triangle together:
| In[4]:= |
| Out[4]= | 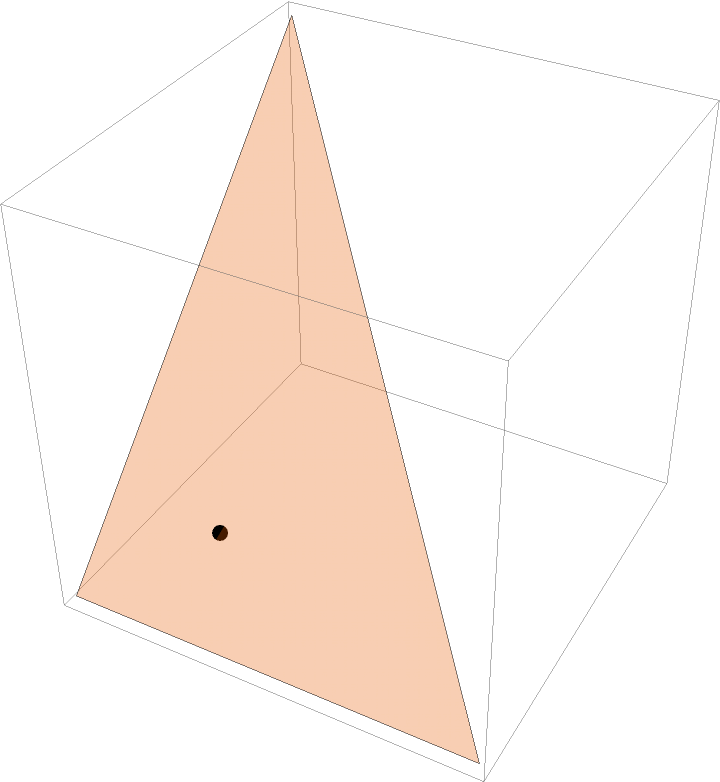 |
The Gergonne point, incenter and de Longchamps point (Kimberling center X20) are collinear:
| In[5]:= | ![tri = {{0, 0}, {1, 5}, {5, 0}};
circumcenter = TriangleConstruct[tri, "Circumcenter"];
orthocenter = TriangleConstruct[tri, "Orthocenter"];
incenter = TriangleConstruct[tri, "Incenter"];](https://www.wolframcloud.com/obj/resourcesystem/images/633/63365a9b-5f50-4cf7-aa9d-b21b97a271e6/4a15f547c61e25f9.png) |
| In[6]:= | ![x20 = Point[
ReflectionTransform[orthocenter[[1]] - circumcenter[[1]], circumcenter[[1]]][orthocenter[[1]]]];
ge = ResourceFunction["GergonnePoint"][tri];](https://www.wolframcloud.com/obj/resourcesystem/images/633/63365a9b-5f50-4cf7-aa9d-b21b97a271e6/2281ed66ac9ea349.png) |
Show the collinearity:
| In[7]:= |
| Out[7]= |
Visualize the points and the line passing them:
| In[8]:= | ![label[sym_, Point[pos_]] := {PointSize[Scaled[0.063]], Hue[0.58, 1, 1], Point[pos], Text[Style[sym, White, FontSize -> Scaled[0.03]], pos]};
Graphics[{
{Orange, Opacity[0.2], Triangle[tri]},
TriangleConstruct[tri, "Incircle"],
InfiniteLine[Identity @@@ {ge, incenter}],
MapThread[
label, {{"Ge", "I", Subscript[X, 20]}, {ge, incenter, x20}}]
}, PlotRange -> {{0, 5}, {-1/3, 5}}]](https://www.wolframcloud.com/obj/resourcesystem/images/633/63365a9b-5f50-4cf7-aa9d-b21b97a271e6/05b84089a73a817c.png) |
| Out[8]= | 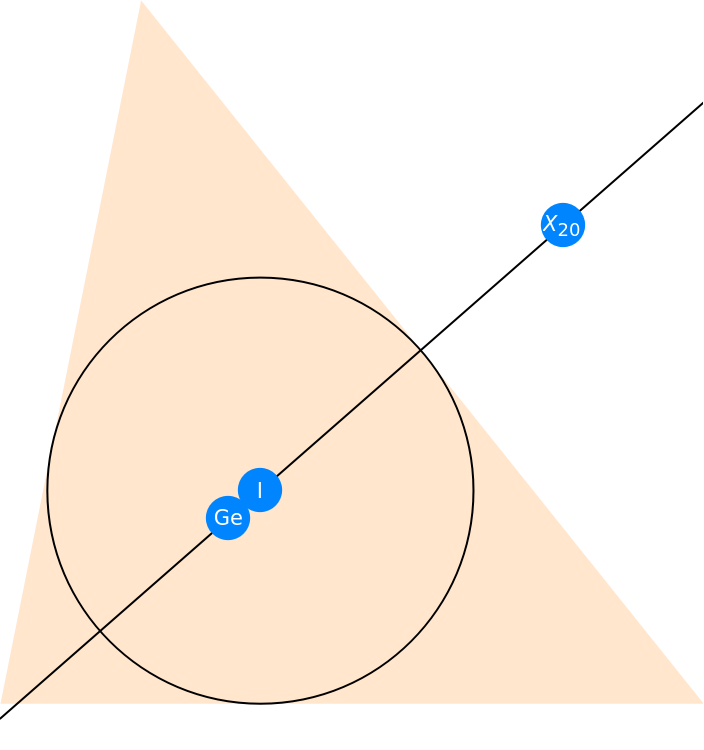 |
This work is licensed under a Creative Commons Attribution 4.0 International License