Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Smooth curve interpolation based on local procedures for a multiple-valued curve
ResourceFunction["AkimaSpline"][{x1,y1},{x2,y2},…}] represents an Akima-spline function defined by the data {xi, yi}. |
Construct an Akima-spline curve using a list of data points:
| In[1]:= |
| In[2]:= |
| Out[2]= |
Apply the function to find a point on the curve:
| In[3]:= |
| Out[3]= |
Plot the Akima-spline curve with the data points:
| In[4]:= |
| Out[4]= | 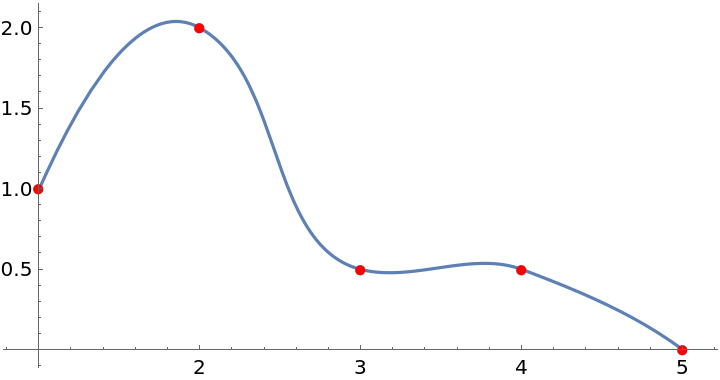 |
Ordinate values can be repeated:
| In[5]:= |
| In[6]:= |
Plot the Akima-spline curve with the data points:
| In[7]:= |
| Out[7]= | 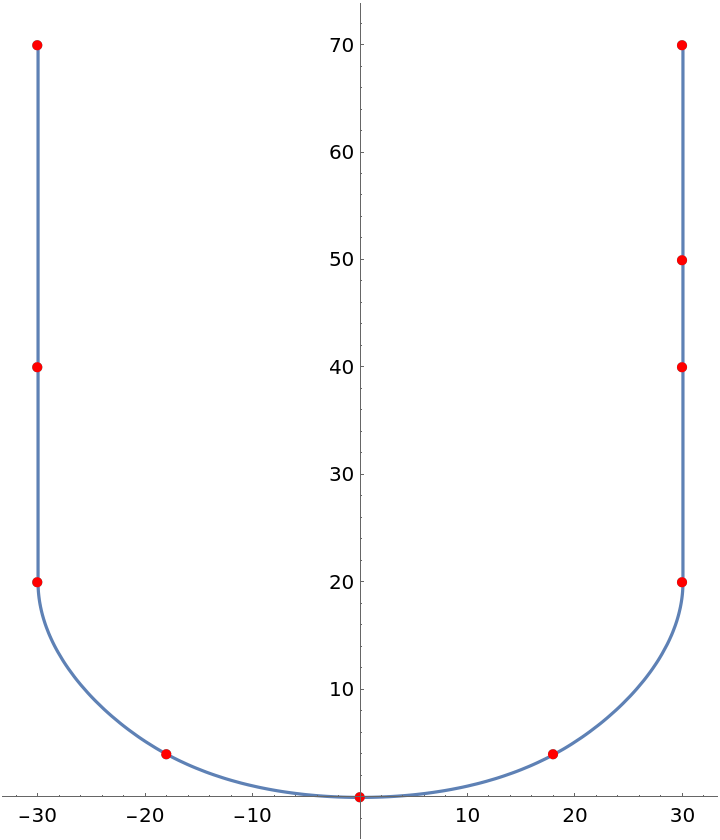 |
| In[8]:= |
| In[9]:= |
| Out[9]= |
Plot the Akima-spline curve with the data points:
| In[10]:= |
| Out[10]= | 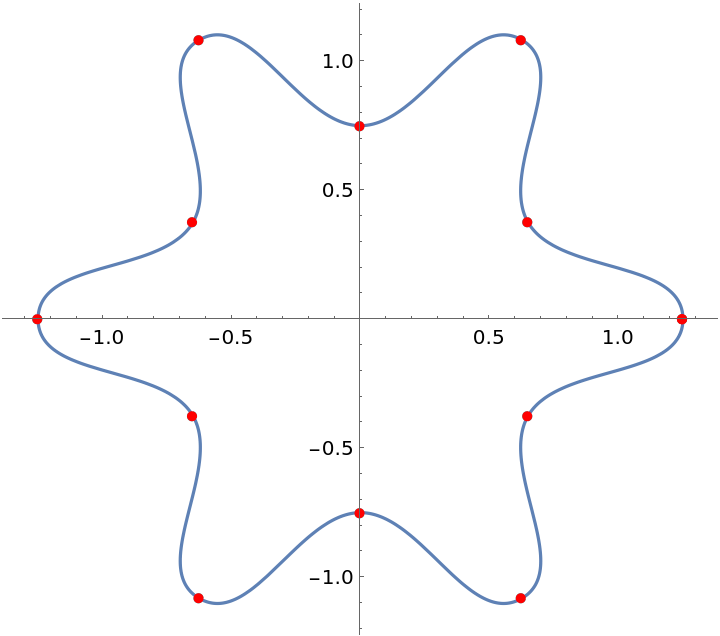 |
Interpolate random data:
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= | 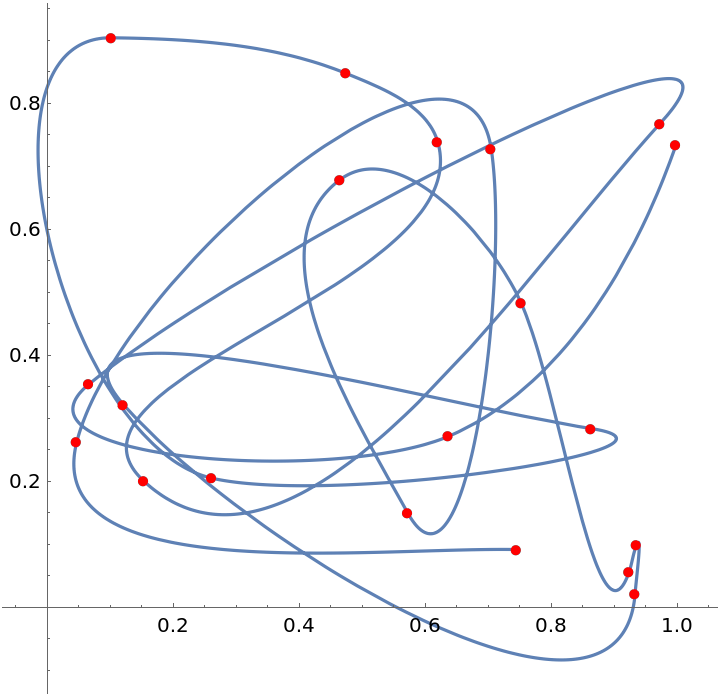 |
Sort the points into a traveling salesman tour:
| In[13]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= |
| In[15]:= |
| Out[15]= | 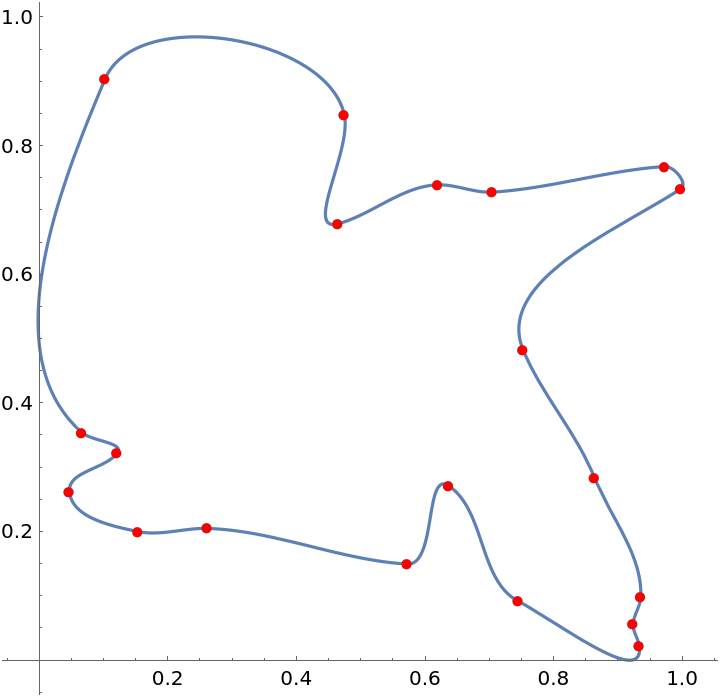 |
Interesting knot-like figures can be drawn:
| In[16]:= | ![input = {{1, 1}, {0, -0.5}, {-1, 1}, {0.5, 0}, {-1, -1}, {0, 0.5}, {1, -1}, {-0.5, 0}, {1, 1}};
ifun = ResourceFunction["AkimaSpline"][input, PeriodicInterpolation -> True];
ParametricPlot[ifun[z], {z, 0, 1}, Axes -> False, Frame -> True, AspectRatio -> 1, PlotRange -> All, Epilog -> {Red, PointSize[0.02], Point[input]}]](https://www.wolframcloud.com/obj/resourcesystem/images/560/56058e84-6431-4180-806e-081c7e4cb2ad/376af787e9ed990f.png) |
| Out[18]= | 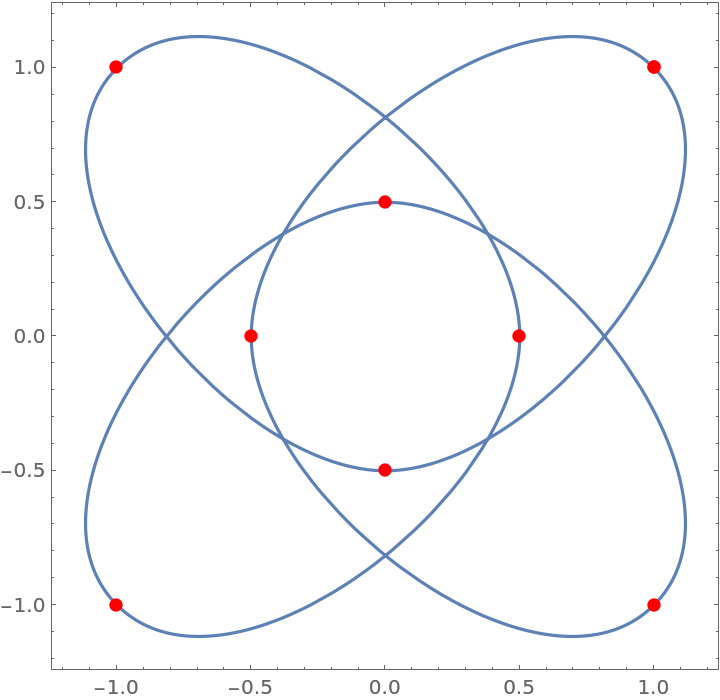 |
A “braided” Spikey:
| In[19]:= |
| In[20]:= | ![points = FirstCase[spikeyData, GraphicsComplex[p_, _] :> p, {}, \[Infinity]];
edges = UndirectedEdge @@@ Join @@ (Partition[#, 2, 1] &) /@ Cases[spikeyData, Line[p_] :> p, \[Infinity]];
gr = Graph[edges, ImageSize -> Small]](https://www.wolframcloud.com/obj/resourcesystem/images/560/56058e84-6431-4180-806e-081c7e4cb2ad/5630c02002366407.png) |
| Out[22]= | 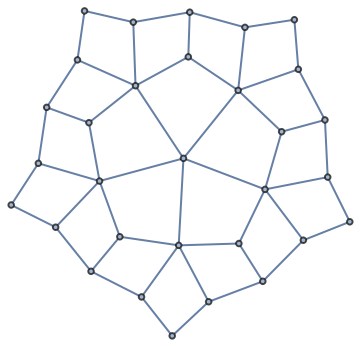 |
| In[23]:= | ![cycles = FindCycle[gr, {6}, All];
vertexLists = Function[cycle, With[{v = First /@ cycle}, Append[v, First@v]]] /@ cycles;
lists = With[{keyVertices = {3, 9, 15, 21, 27}}, Cases[Cases[vertexLists, {___, #, ___}], l_ /; FreeQ[l, Alternatives @@ DeleteCases[keyVertices, #]]] & /@
keyVertices];](https://www.wolframcloud.com/obj/resourcesystem/images/560/56058e84-6431-4180-806e-081c7e4cb2ad/3d5683b535ec07f4.png) |
| In[24]:= |
| Out[24]= |  |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License