Basic Examples (2) 

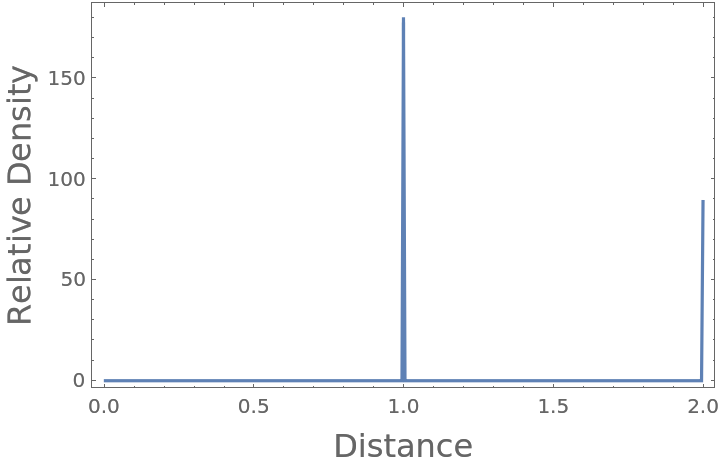
Compute the radial distribution function from two points:

In[1]:=

Out[1]=

Compute the radial distribution function of a set of coordinates enclosed in a periodic 1D "box" of size (L = 4):

In[2]:=

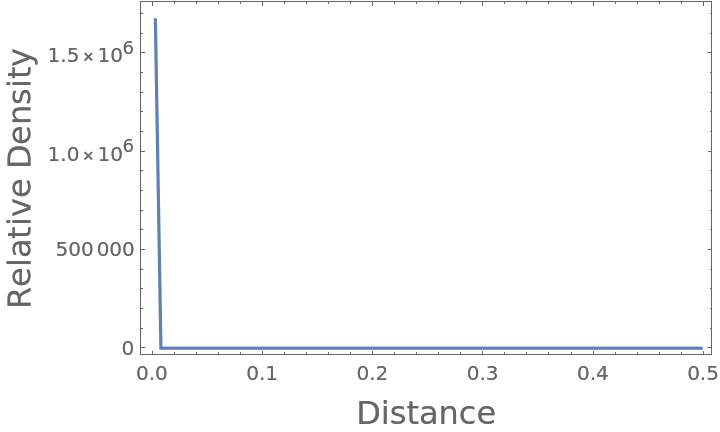
Display the coordinates in number line format along the axis for which the positions differ:

In[3]:=

Out[3]=

The radial distribution function has non-zero peaks at positions near those of the exact distances apart:

In[4]:=

Out[4]=

Plot the radial distribution function characteristic of this system:

In[5]:=

Out[5]=

Options (2) 

Cross-correlations can be computed using the option "ReferenceCoordinates":

In[6]:=

Out[7]=

Radial distribution function takes the same options as Compile, and benefits from automated compilation to C:

In[8]:=

Out[8]=

In[9]:=

Out[9]=

Applications (2) 

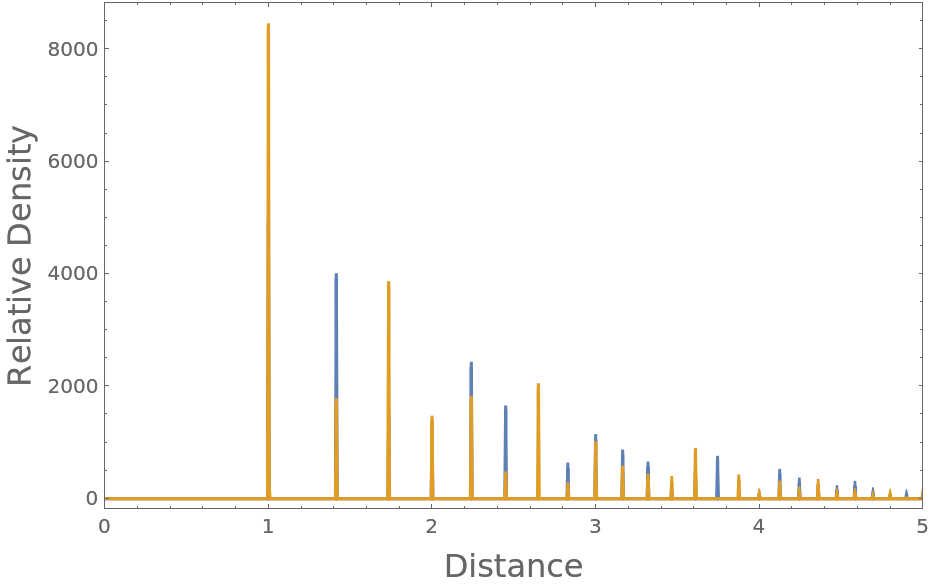
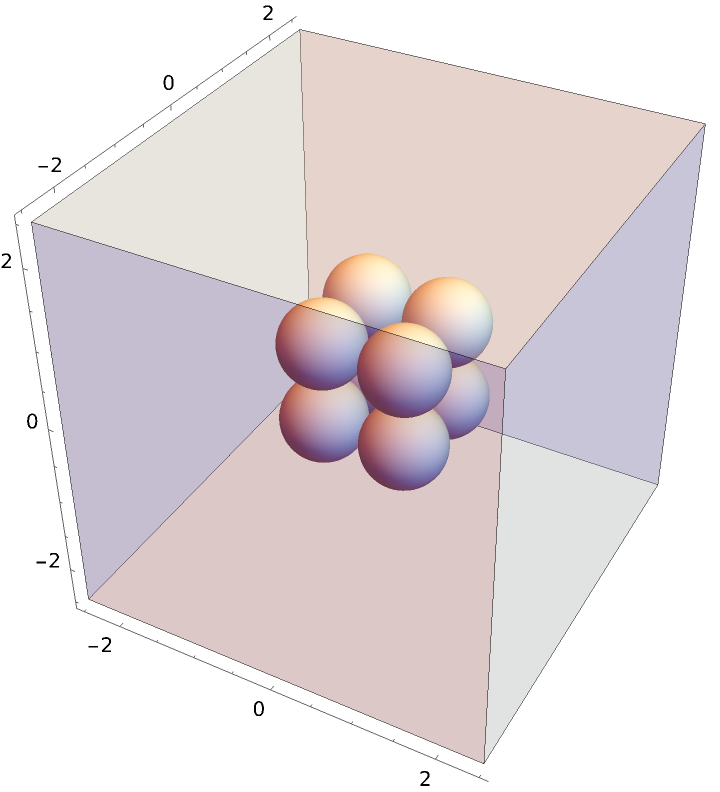
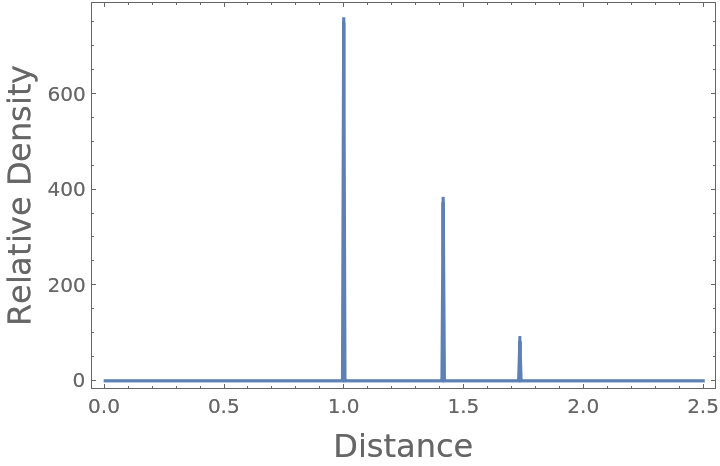
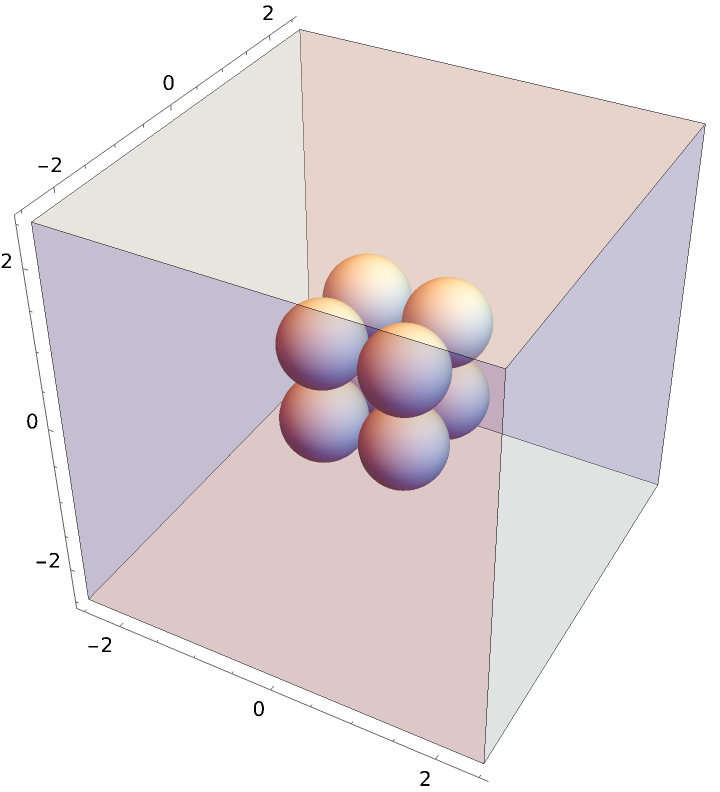
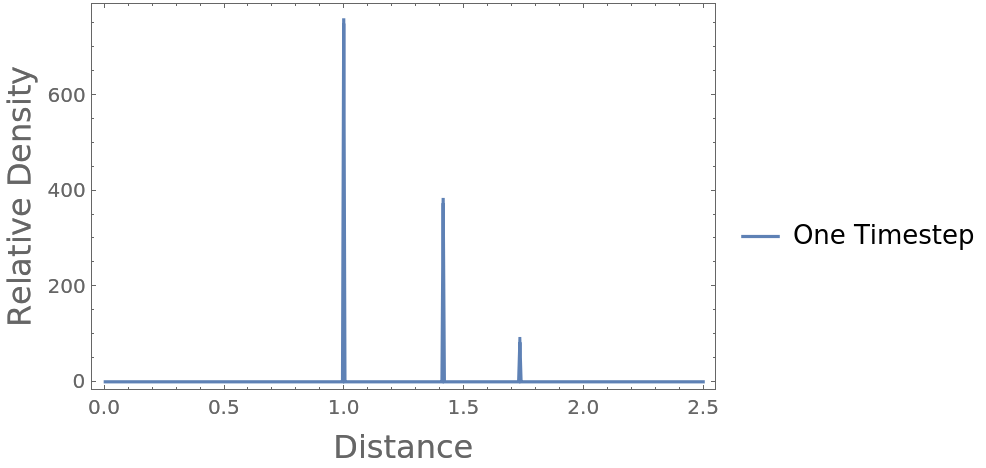
Compute the radial distribution function characteristic of a cube with unit length, enclosed in a sufficiently larger periodic box:

In[10]:=

Out[11]=

Plot the resulting radial distribution function, where you can see nearest neighbor, polygonal face hypotenuse, and internal hypotenuse distances:

In[12]:=

Out[12]=

Properties and Relations (4) 

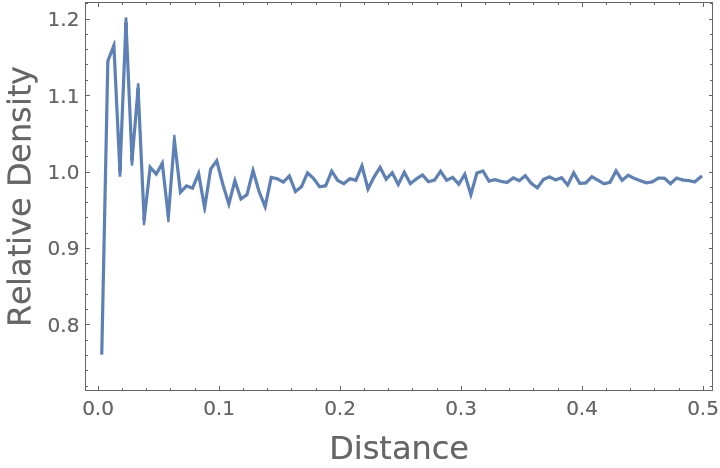
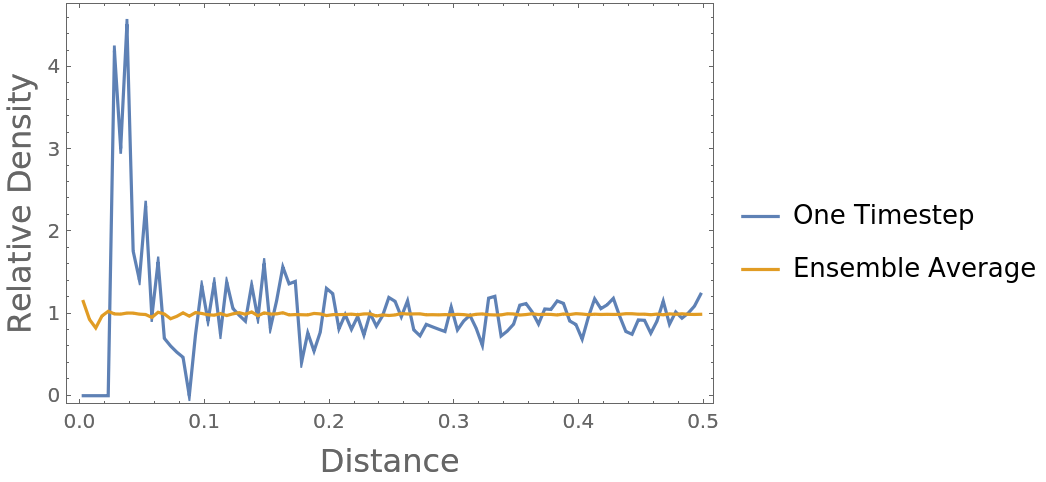
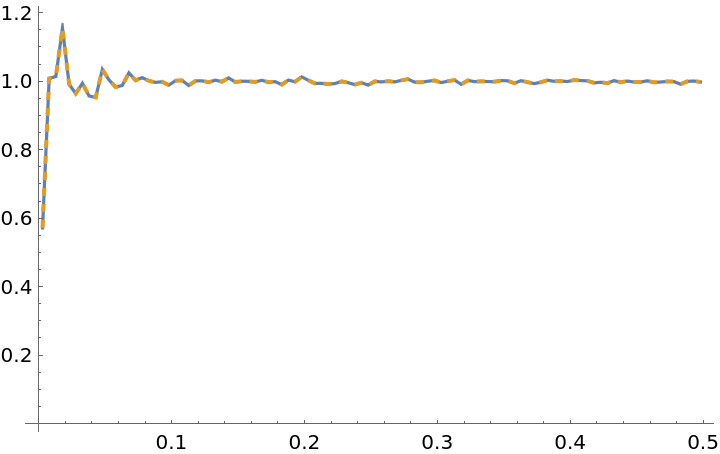
By definition, the RDF of an ideal gas converges to 1 at all distances when provided sufficient data (here, 1000 time steps on 100 positions of 100 particles):

In[13]:=

Compute both the radial distribution function of just the first time step, and then that of the ensemble average over all time steps:

In[14]:=

As expected, the radial distribution function converges to nearly 1 as sufficient data is introduced:

In[15]:=

Out[15]=

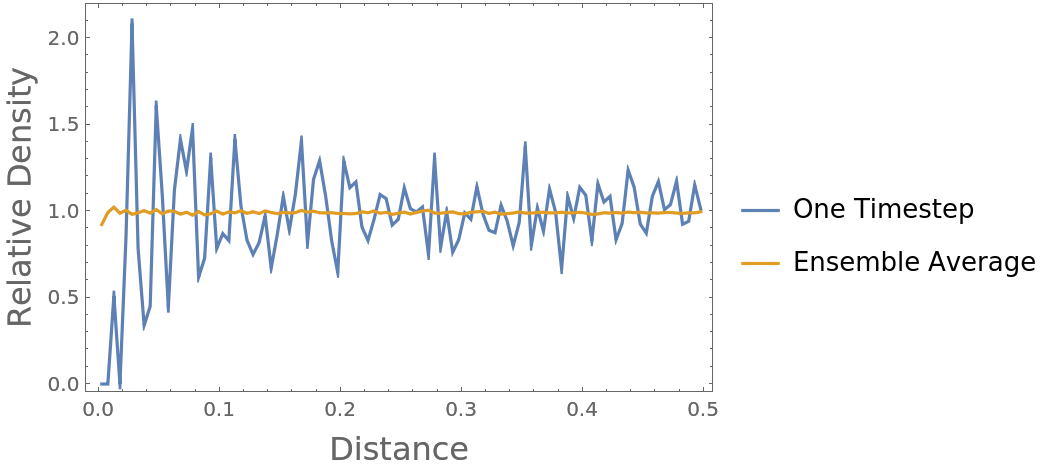
Normalization by the expected number of particles in that vicinity works in 2D cases as well:

In[16]:=

In[17]:=

Out[17]=

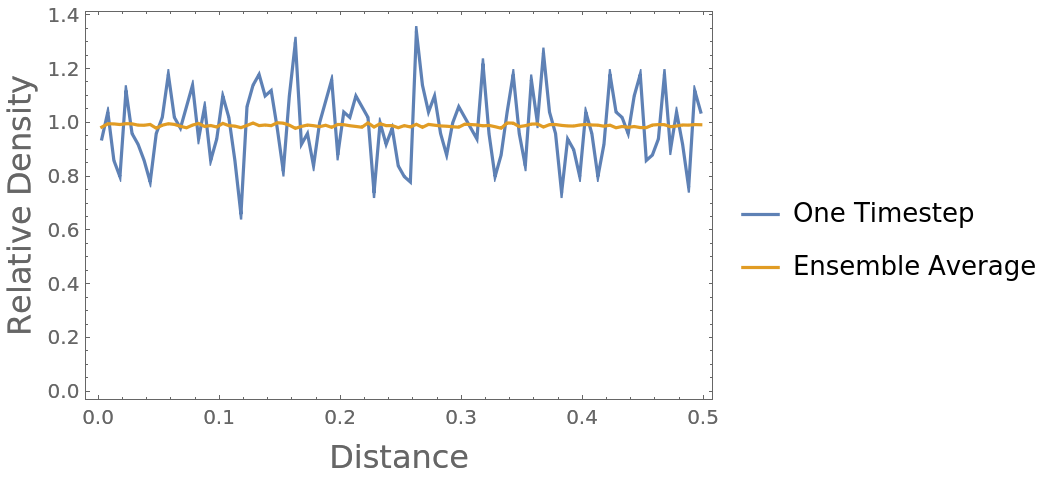
The same is true for 1D cases:

In[18]:=

In[19]:=

Out[19]=

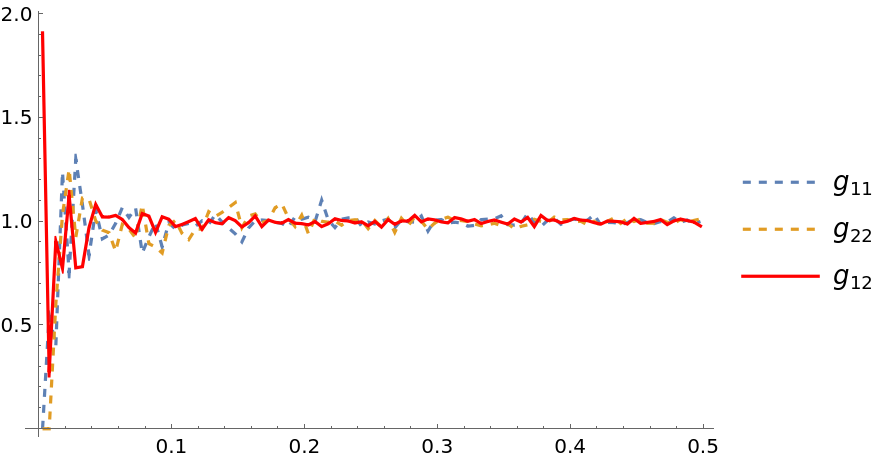
Ensemble average cross-correlations between two distinct populations (lists of coordinates) can also be computed:

In[20]:=

Out[21]=

Cross-correlations are symmetric, that is, the computation is the same for swapped populations g_{{XMLElement[i, {}, {XMLElement[span, {class -> stylebox}, {ij}]}]}}(r)=g_{{XMLElement[i, {}, {XMLElement[span, {class -> stylebox}, {ji}]}]}}(r):

In[22]:=

Out[8]=

In[23]:=

Out[23]=

Possible Issues (4) 

For finite-sized systems, the radial distribution function is accurate out to 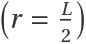and is thus truncated at this point, beyond which it would artificially decay:

In[24]:=

Out[3]=

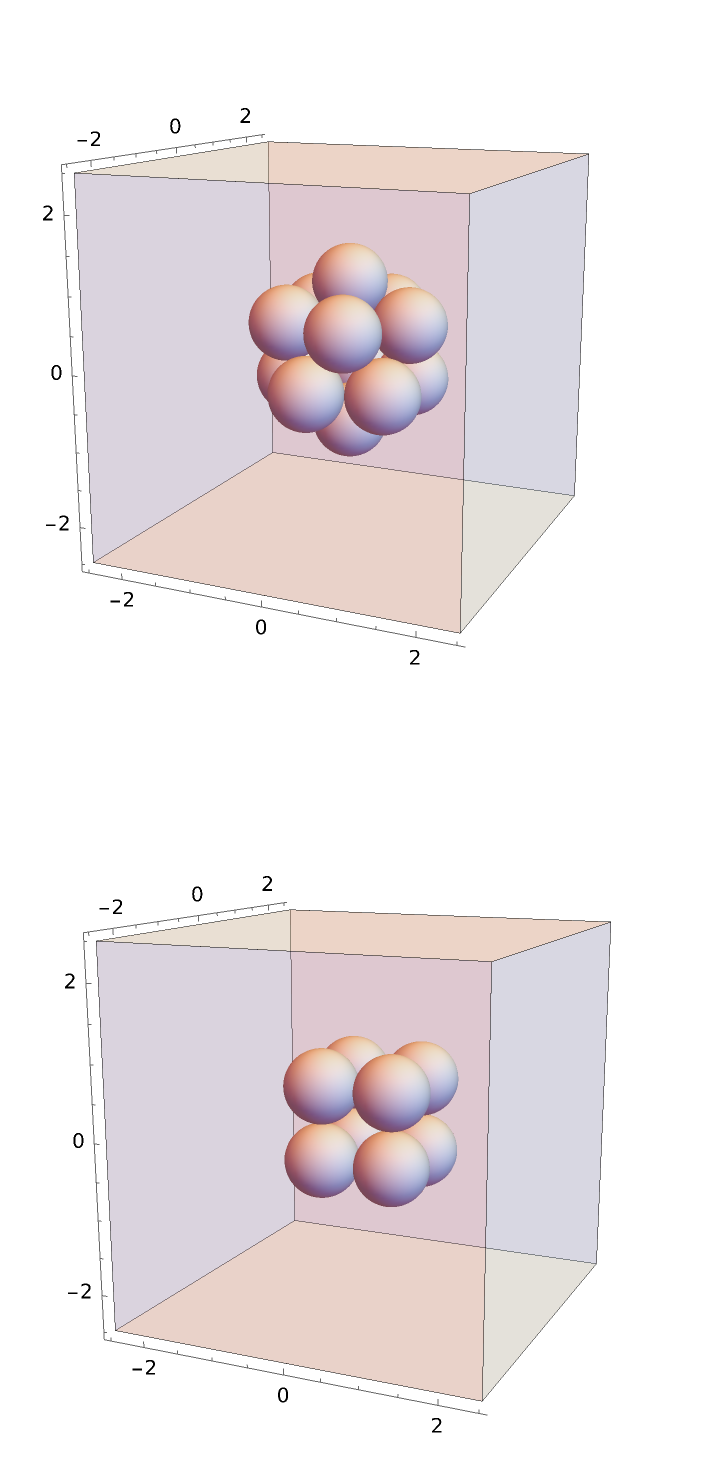
If the box is sufficiently larger than the domain of the particle coordinates, the calculation is as expected (using real particle positions, rather than the minimum image convention under periodicity):

In[25]:=

Out[26]=

The peaks are at the expected unit distance for the touching particles, at the polygonal face hypotenuse distance, and the interior hypotenuse:

In[27]:=

Out[27]=

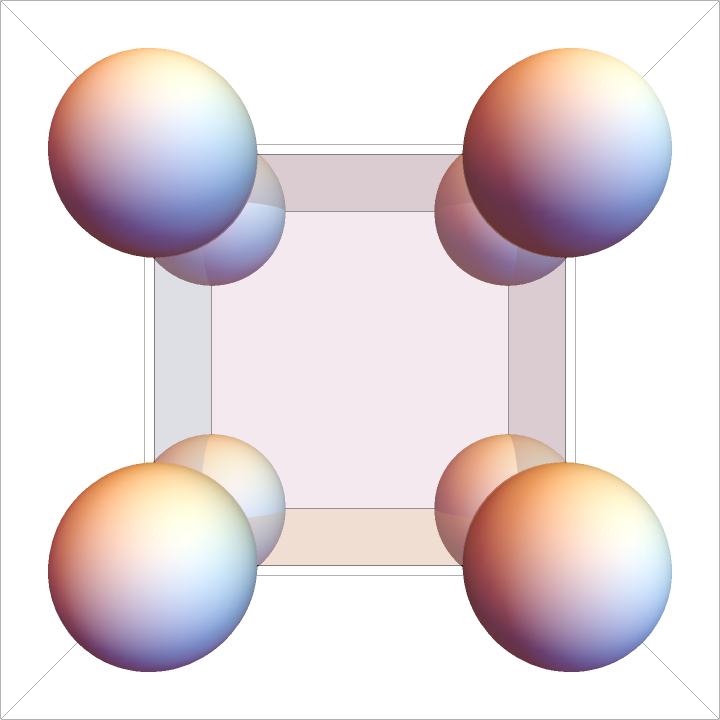
If the box size (L) is too small, the minimum image convention is employed, applying periodicity in each dimension:

In[28]:=

Out[31]=

In this case, particles are perfectly overlapping and the separation distance between all pairs is r_{{XMLElement[i, {}, {XMLElement[span, {class -> stylebox}, {ij}]}]}}=0, however the convention is to put them in the first non-zero bin:

In[32]:=

Out[32]=

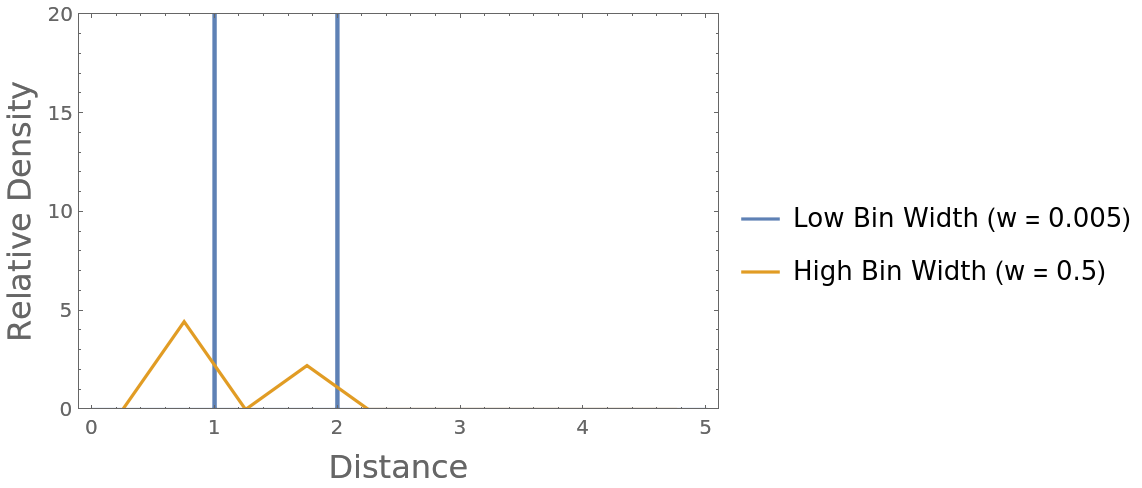
Modifying the concentric shell bin width can affect normalization and positional accuracy, similar to the behavior in Riemann sums with too few discretizing rectangles:

In[33]:=

Out[35]=

Compare the difference when using two different bin widths:

In[36]:=

Out[38]=

Neat Examples (3) 

Compute the radial distribution function characteristic of an icosahedral distribution of particles and compare it with that of a cube, each with a minimum separation distance of 1:

In[39]:=

Out[43]=

Plot the resulting radial distribution functions to compare:

In[44]:=

Out[44]=

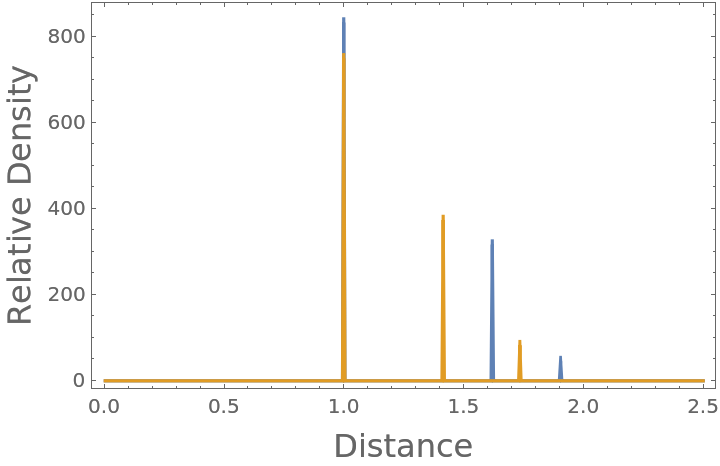
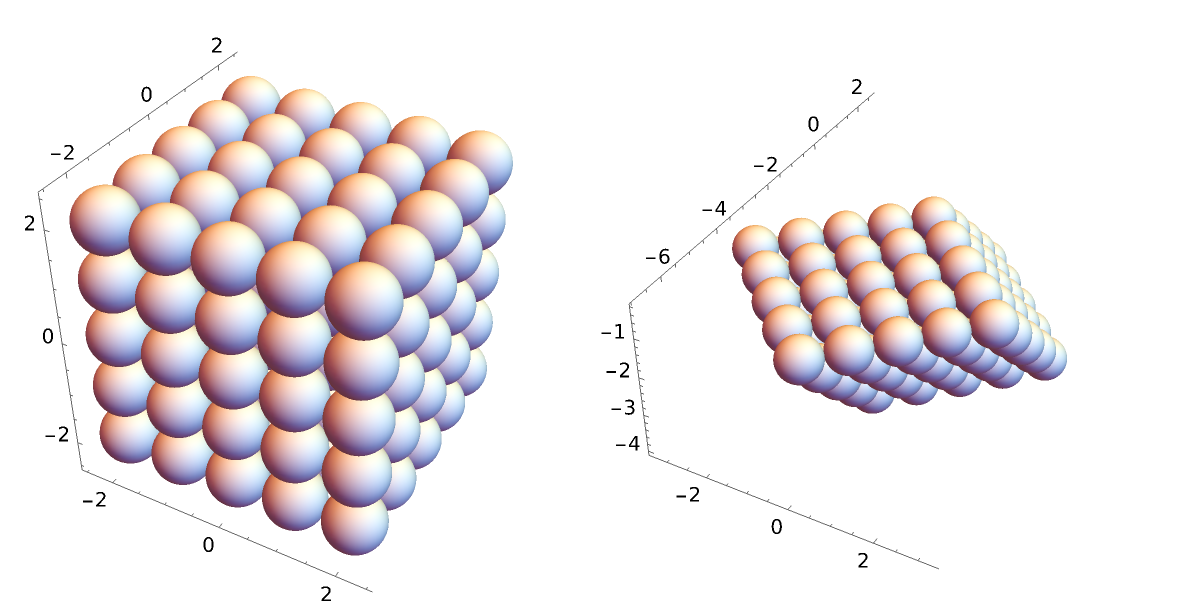
Compare the radial distribution function of both a simple cubic and face-centered cubic (FCC) crystalline lattice (neglecting periodicity, each with nearest neighbors touching at unit lengths):

In[45]:=

Out[49]=

Compute and plot the radial distribution functions to compare:

In[50]:=

Out[51]=

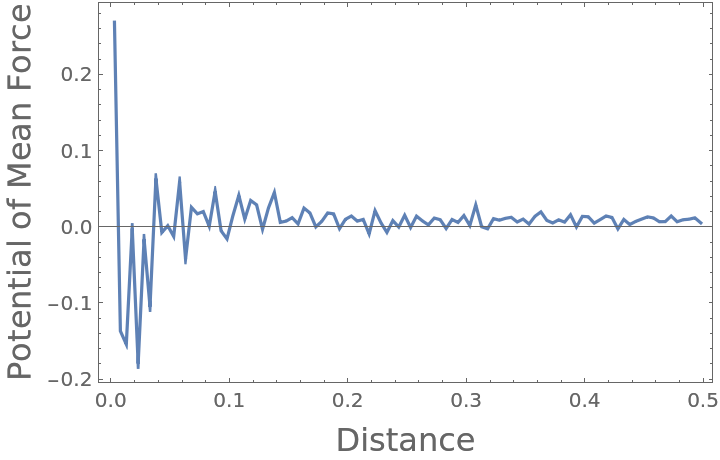
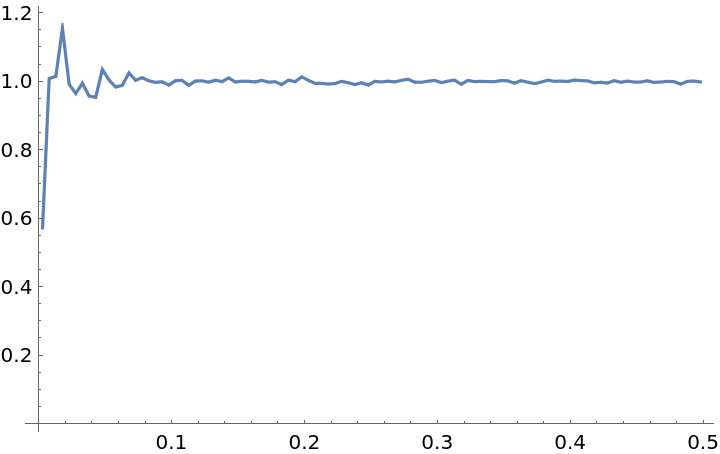
Compute the Potential of Mean Force that has given rise to the interactions, in this example showing that the 3D ideal gas has no potential of interaction:

In[52]:=

In[53]:=

Out[53]=

Compute the corresponding Potential of Mean Force (in units where k_BT=1):

In[54]:=

In[55]:=

Out[55]=

It can be seen that despite the noise associated finite data, the Potential of Mean Force is fairly close to zero when averaged over the entire domain:

In[56]:=

Out[56]=