Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language
As of Version 14.3, LommelS2 is a built-in symbol.

Function Repository Resource:

 LommelS

Source Notebook

Evaluate the Lommel function

Contributed by: Jan Mangaldan

ResourceFunction["LommelS"][μ,ν,z]

gives the Lommel function Sμ,ν(z).

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
Sμ,ν(z) satisfies the differential equation .
ResourceFunction["LommelS"][μ,ν,z] has a branch cut discontinuity in the complex z plane running from -∞ to 0.
For certain special arguments, ResourceFunction["LommelS"] automatically evaluates to exact values.
ResourceFunction["LommelS"] can be evaluated to arbitrary numerical precision.
ResourceFunction["LommelS"] automatically threads over lists.

Examples

Basic Examples (3) 

Evaluate numerically:

In[1]:=
ResourceFunction["LommelS"][-0.25, 2/3, 1]
Out[1]=

Plot S-1/4,2/3(x) over a subset of the reals:

In[2]:=
Plot[ResourceFunction["LommelS"][-1/4, 2/3, x], {x, 0, 5}]
Out[2]=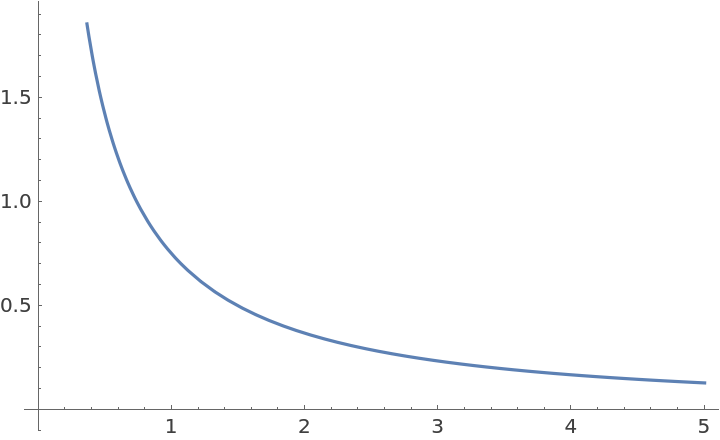

Series expansion at the origin:

In[3]:=
Series[ResourceFunction["LommelS"][-2, 4, z], {z, 0, 5}]
Out[3]=

Scope (4) 

Evaluate for complex arguments:

In[4]:=
ResourceFunction["LommelS"][2.1 + 1.3 I, -1.7 + 2. I, 0.6 - 0.2 I]
Out[4]=

Evaluate to high precision:

In[5]:=
N[ResourceFunction["LommelS"][2/3, 1/2, 4/5], 50]
Out[5]=

The precision of the output tracks the precision of the input:

In[6]:=
ResourceFunction["LommelS"][2/3, 1/2, 0.800000000000000000000000000]
Out[6]=

LommelS threads elementwise over lists:

In[7]:=
ResourceFunction["LommelS"][{2, 3, 5}, 1/2, 1.]
Out[7]=

Simple exact values are generated automatically:

In[8]:=
ResourceFunction["LommelS"][-2, -3, 1]
Out[8]=

Properties and Relations (7) 

Verify recurrence relations satisfied by LommelS:

In[9]:=
With[{\[Mu] = 2, \[Nu] = 3}, ResourceFunction["LommelS"][\[Mu] + 2, \[Nu], z] == z^(\[Mu] + 1) - ((\[Mu] + 1)^2 - \[Nu]^2) ResourceFunction[ "LommelS"][\[Mu], \[Nu], z] // FullSimplify]
Out[9]=
In[10]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/b894f08b-a7b8-466b-bf3f-403bfdffe4e2"]
Out[10]=

Express the derivative of LommelS in terms of LommelS:

In[11]:=
With[{\[Mu] = 2, \[Nu] = 3}, D[ResourceFunction["LommelS"][\[Mu], \[Nu], z], z] == \[Nu]/ z ResourceFunction["LommelS"][\[Mu], \[Nu], z] + (\[Mu] - \[Nu] - 1) ResourceFunction[ "LommelS"][\[Mu] - 1, \[Nu] + 1, z] // FullSimplify]
Out[11]=
In[12]:=
With[{\[Mu] = 2, \[Nu] = 3}, D[ResourceFunction["LommelS"][\[Mu], \[Nu], z], z] == -(\[Nu]/z) ResourceFunction["LommelS"][\[Mu], \[Nu], z] + (\[Mu] + \[Nu] - 1) ResourceFunction[ "LommelS"][\[Mu] - 1, \[Nu] - 1, z] // FullSimplify]
Out[12]=
In[13]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/daee2cf7-fe31-4c6e-b2f7-5133dd25a85f"]
Out[13]=

Indefinite integrals of the Bessel functions BesselJ and BesselY multiplied by a power function can be expressed in terms of Bessel functions and LommelS:

In[14]:=
With[{\[Mu] = 2, \[Nu] = 3}, D[(\[Mu] + \[Nu] - 1) z BesselJ[\[Nu], z] ResourceFunction[ "LommelS"][\[Mu] - 1, \[Nu] - 1, z] - z BesselJ[\[Nu] - 1, z] ResourceFunction["LommelS"][\[Mu], \[Nu], z], z] == z^\[Mu] BesselJ[\[Nu], z] // FullSimplify]
Out[14]=
In[15]:=
With[{\[Mu] = 2, \[Nu] = 3}, D[(\[Mu] + \[Nu] - 1) z BesselY[\[Nu], z] ResourceFunction[ "LommelS"][\[Mu] - 1, \[Nu] - 1, z] - z BesselY[\[Nu] - 1, z] ResourceFunction["LommelS"][\[Mu], \[Nu], z], z] == z^\[Mu] BesselY[\[Nu], z] // FullSimplify]
Out[15]=

Express the Anger and Weber functions in terms of LommelS:

In[16]:=
AngerJ[n, z] == BesselJ[n, z] + Sin[n \[Pi]]/\[Pi] (ResourceFunction["LommelS"][0, n, z] - n ResourceFunction["LommelS"][-1, n, z]) // FullSimplify
Out[16]=
In[17]:=
WeberE[n, z] == -BesselY[n, z] - ( 1 - Cos[n \[Pi]])/\[Pi] n ResourceFunction["LommelS"][-1, n, z] - (1 + Cos[n \[Pi]])/\[Pi] ResourceFunction["LommelS"][0, n, z] // FunctionExpand // FullSimplify
Out[17]=

The associated Anger–Weber function AngerWeberA can be expressed in terms of LommelS:

In[18]:=
ResourceFunction["AngerWeberA"][n, z] == ( ResourceFunction["LommelS"][0, n, z] - n ResourceFunction["LommelS"][-1, n, z])/\[Pi] // FullSimplify
Out[18]=

The Neumann polynomial NeumannO can be expressed in terms of LommelS:

In[19]:=
Table[ResourceFunction["NeumannO"][n, z] == Binomial[n, Mod[n, 2]]/ z ResourceFunction["LommelS"][1 - Mod[n, 2], n, z], {n, 0, 10}] // Simplify
Out[19]=

The Schläfli polynomial SchlaefliS can be expressed in terms of LommelS:

In[20]:=
Table[ResourceFunction["SchlaefliS"][n, z] == (n + 1 + (n - 1) (-1)^n) ResourceFunction[ "LommelS"][-Mod[n + 1, 2], n, z], {n, 0, 10}] // Simplify
Out[20]=

Version History

  • 1.1.0 – 14 September 2021
  • 1.0.0 – 07 January 2021

Source Metadata

  • Citation:
    • "Lommel Functions." §11.9 in F. W. J. Olver et al. (eds.), NIST Digital Library of Mathematical Functions. https://dlmf.nist.gov/11.9. Release 1.1.0 of 2020-12-15.

Related Resources

Author Notes

Watson's book and the DLMF associate two functions with Lommel, denoted sμ,ν(z) and Sμ,ν(z). LommelS implements the latter one, since the former is undefined when μ±ν is an odd negative integer.

License Information