Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the associated Anger–Weber function
ResourceFunction["AngerWeberA"][ν,z] gives the associated Anger–Weber function |
Evaluate numerically:
| In[1]:= |
| Out[1]= |
Plot ![]() :
:
| In[2]:= |
| Out[2]= | 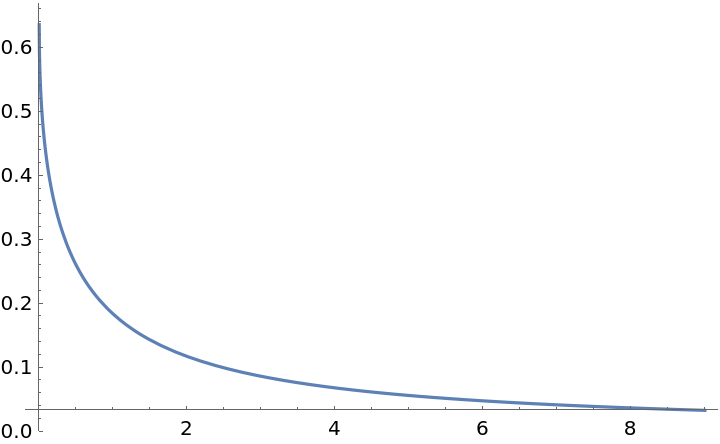 |
Evaluate for complex arguments:
| In[3]:= |
| Out[3]= |
Evaluate to arbitrary precision:
| In[4]:= |
| Out[4]= |
The precision of the output tracks the precision of the input:
| In[5]:= |
| Out[5]= |
Simple exact values are generated automatically:
| In[6]:= |
| Out[6]= |
AngerWeberA threads elementwise over lists:
| In[7]:= |
| Out[7]= |
Use FunctionExpand to expand AngerWeberA into hypergeometric functions:
| In[8]:= |
| Out[8]= | 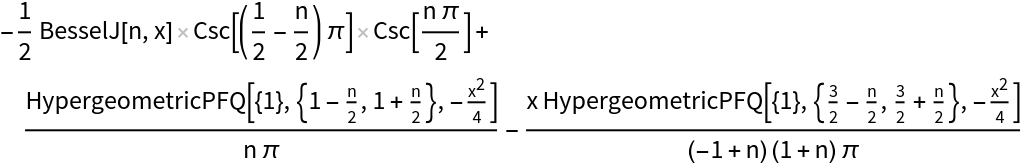 |
Compare AngerWeberA with the integral definition:
| In[9]:= | ![With[{n = 5, z = 11/3, prec = 20}, {N[ResourceFunction["AngerWeberA"][n, z], prec], NIntegrate[Exp[-n t - z Sinh[t]], {t, 0, Infinity}, WorkingPrecision -> prec]/Pi}]](https://www.wolframcloud.com/obj/resourcesystem/images/425/425b1b4d-0568-45dc-98a3-e9760c47b52f/1219263b6b0a78fa.png) |
| Out[9]= |
Express AngerWeberA in terms of the Lommel function LommelS:
| In[10]:= | ![FullSimplify[
ResourceFunction["AngerWeberA"][n, z] == 1/\[Pi] (ResourceFunction["LommelS"][0, n, z] - n ResourceFunction["LommelS"][-1, n, z])]](https://www.wolframcloud.com/obj/resourcesystem/images/425/425b1b4d-0568-45dc-98a3-e9760c47b52f/0565fb6b4edaa706.png) |
| Out[10]= |
Verify a differential equation for AngerWeberA:
| In[11]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/a70713bf-bc5a-41cc-9edc-dddc2e6ee7f7"]](https://www.wolframcloud.com/obj/resourcesystem/images/425/425b1b4d-0568-45dc-98a3-e9760c47b52f/6fee0b07fcfa08b0.png) |
| Out[11]= |
Verify a recurrence identity for AngerWeberA:
| In[12]:= | ![Table[ResourceFunction["AngerWeberA"][n + 1, z] + ResourceFunction["AngerWeberA"][n - 1, z] == 2/(\[Pi] z) - (2 n)/z ResourceFunction["AngerWeberA"][n, z] /. z -> RandomComplex[WorkingPrecision -> 20], {n, 9}]](https://www.wolframcloud.com/obj/resourcesystem/images/425/425b1b4d-0568-45dc-98a3-e9760c47b52f/627d24c6eb4d0bee.png) |
| Out[12]= |
An identity relating AngerWeberA and AngerJ:
| In[13]:= |
| Out[13]= |
An identity relating AngerWeberA and WeberE:
| In[14]:= |
| Out[14]= |
This work is licensed under a Creative Commons Attribution 4.0 International License