Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the Schläfli polynomial
ResourceFunction["SchlaefliS"][n,z] gives the Schläfli polynomial Sn(z) . |
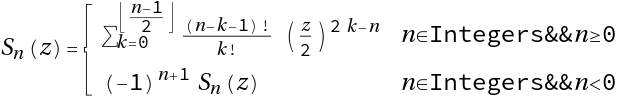
Evaluate numerically:
| In[1]:= |
| Out[1]= |
Evaluate Schläfli polynomials for various orders:
| In[2]:= |
| Out[2]= |
Plot with respect to z:
| In[3]:= |
| Out[3]= | 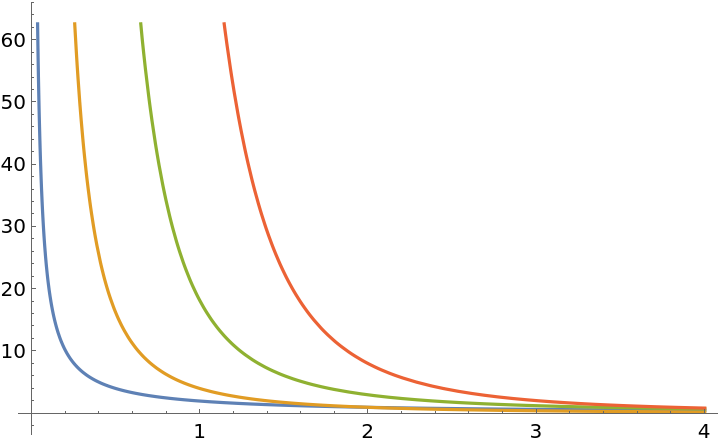 |
Evaluate for complex arguments:
| In[4]:= |
| Out[4]= |
Evaluate to high precision:
| In[5]:= |
| Out[5]= |
The precision of the output tracks the precision of the input:
| In[6]:= |
| Out[6]= |
SchlaefliS threads elementwise over lists:
| In[7]:= |
| Out[7]= |
The Schläfli polynomial can be expressed in terms of the Neumann polynomial NeumannO:
| In[8]:= | ![Table[n/2 ResourceFunction["SchlaefliS"][n, t] == t ResourceFunction["NeumannO"][n, t] - Cos[(n \[Pi])/2]^2 // Simplify, {n, -3, 3}]](https://www.wolframcloud.com/obj/resourcesystem/images/c27/c2730561-1146-4279-91d8-523c8bb2c12e/20905930a826b35c.png) |
| Out[8]= |
The Schläfli polynomial can be expressed in terms of the Lommel function LommelS:
| In[9]:= | ![Table[ResourceFunction["SchlaefliS"][n, z] == (n + 1 + (n - 1) (-1)^n) ResourceFunction[
"LommelS"][-Mod[n + 1, 2], n, z], {n, 0, 9}] // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/c27/c2730561-1146-4279-91d8-523c8bb2c12e/1a926fa95371e78f.png) |
| Out[9]= |
Verify a differential equation for the Schläfli polynomial:
| In[10]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/fa0f62dd-9461-4052-9036-a3495d6ffd4f"]](https://www.wolframcloud.com/obj/resourcesystem/images/c27/c2730561-1146-4279-91d8-523c8bb2c12e/0e148bccb13ba034.png) |
| Out[10]= |
Verify a recurrence identity for the Schläfli polynomial:
| In[11]:= | ![Table[ResourceFunction["SchlaefliS"][n + 1, z] + ResourceFunction["SchlaefliS"][n - 1, z] - (2 n)/
z ResourceFunction["SchlaefliS"][n, z] == 4/z Cos[(n \[Pi])/2]^2, {n, 0, 9}] // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/c27/c2730561-1146-4279-91d8-523c8bb2c12e/4e92737e12747bdf.png) |
| Out[11]= |
Verify Graf's formula for the Schläfli polynomial:
| In[12]:= | ![Table[ResourceFunction["SchlaefliS"][n, z] == \[Pi] \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = \(-n\)\), \(n\)]\((BesselJ[n, z] BesselY[k, z] - BesselJ[k, z] BesselY[n, z])\)\) // FullSimplify, {n, 0, 9}]](https://www.wolframcloud.com/obj/resourcesystem/images/c27/c2730561-1146-4279-91d8-523c8bb2c12e/656e2bb902d67fde.png) |
| Out[12]= |
This work is licensed under a Creative Commons Attribution 4.0 International License