Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find a quadric surface that passes through nine given 3D points
ResourceFunction["NinePointQuadric"][pts,{x,y,z}] returns the implicit Cartesian equation in the variables x,y and z of the quadric surface that goes through the points pts. | |
ResourceFunction["NinePointQuadric"][pts] uses the formal variables x, y and z. |
Find the quadric surface going through nine points (based of the decimal digits of 927):
| In[1]:= |
| Out[2]= |
Show the quadric surface (a hyperboloid of one sheet) with the points:
| In[3]:= | ![Graphics3D[{ContourPlot3D[
quadric == 0, {x, -3, 12}, {y, -3, 12}, {z, -3, 12}, ContourStyle -> Opacity[0.3]][[1]], {ColorData[97, 4], Sphere[pts, Scaled[0.008]]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/b83/b83b1231-6125-424e-8249-c375abfd87fd/17333c2e7d89ad97.png) |
| Out[3]= | 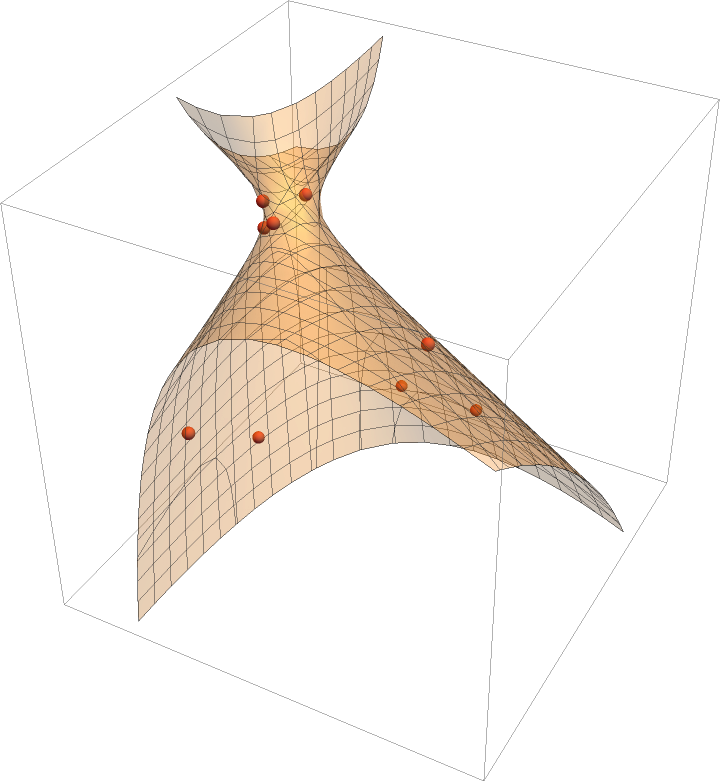 |
Find the quadric surface going through nine points (based of the decimal digits of 928):
| In[4]:= |
| Out[5]= |
Show the quadric surface (a hyperbolic paraboloid) with the points:
| In[6]:= | ![Graphics3D[{ContourPlot3D[
quadric == 0, {x, -3, 12}, {y, -3, 12}, {z, -3, 12}, ContourStyle -> Opacity[0.3]][[1]], {ColorData[97, 4], Sphere[pts, Scaled[0.008]]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/b83/b83b1231-6125-424e-8249-c375abfd87fd/74a74530c1c3493b.png) |
| Out[6]= | 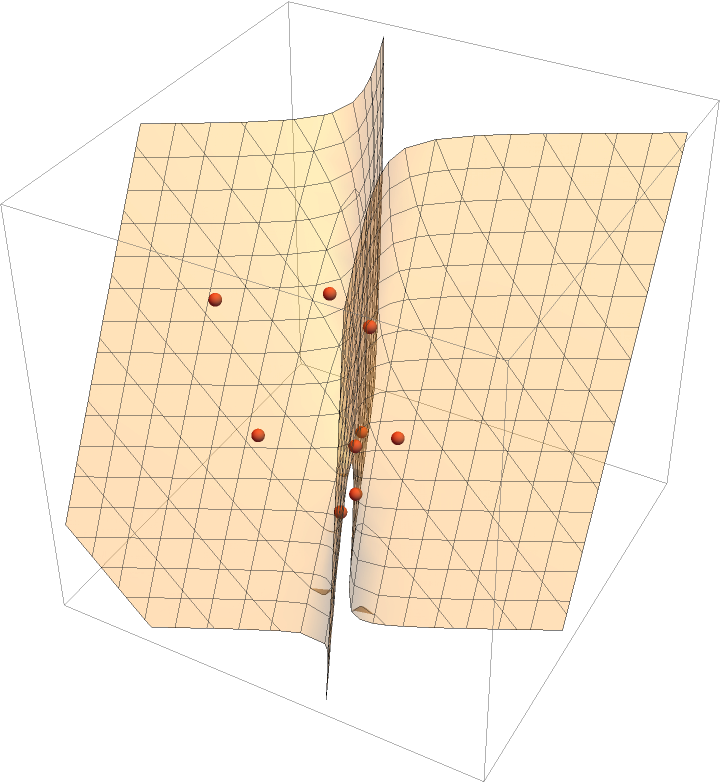 |
Find the quadric surface going through nine points based of the decimal digits of 925:
| In[7]:= |
| Out[8]= |
Show the quadric surface (an ellipsoid) with the points:
| In[9]:= | ![Graphics3D[{ContourPlot3D[
quadric == 0, {x, -3, 12}, {y, -3, 12}, {z, -3, 12}, ContourStyle -> Opacity[0.3]][[1]], {ColorData[97, 4], Sphere[pts, Scaled[0.008]]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/b83/b83b1231-6125-424e-8249-c375abfd87fd/6812a86c9b5f277f.png) |
| Out[9]= | 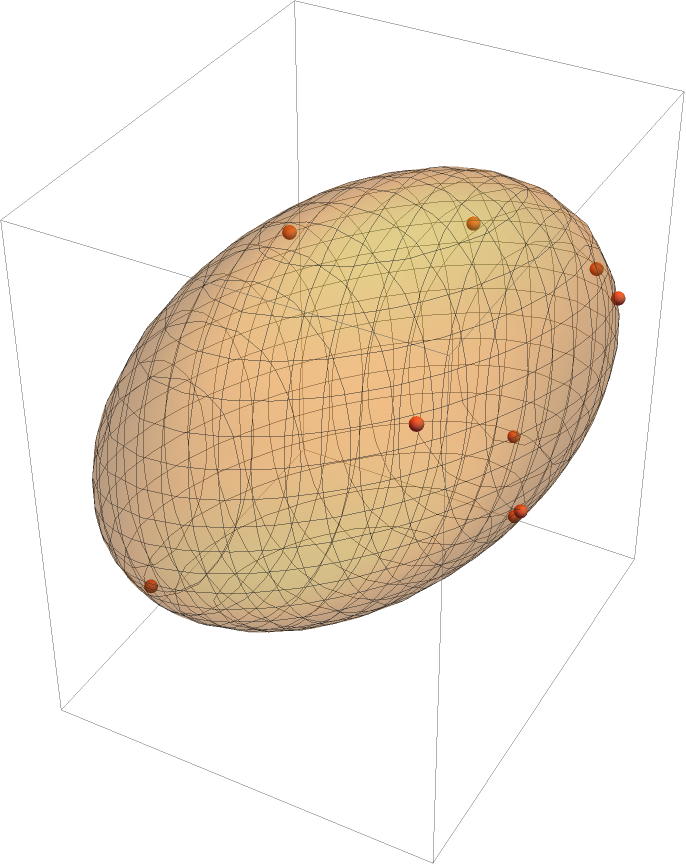 |
Use the resource function QuadricSurfacePlot to show this same ellipsoid:
| In[10]:= | ![ResourceFunction["QuadricSurfacePlot"][-7962557 x + 2547673 x^2 - 5905703 y - 2298838 x y + 1732345 y^2 - 7305719 z - 1057140 x z + 629106 y z + 1014353 z^2, {x, y, z}, "DrawAxes" -> True, Mesh -> None]](https://www.wolframcloud.com/obj/resourcesystem/images/b83/b83b1231-6125-424e-8249-c375abfd87fd/38531197231bf6f2.png) |
| Out[10]= | 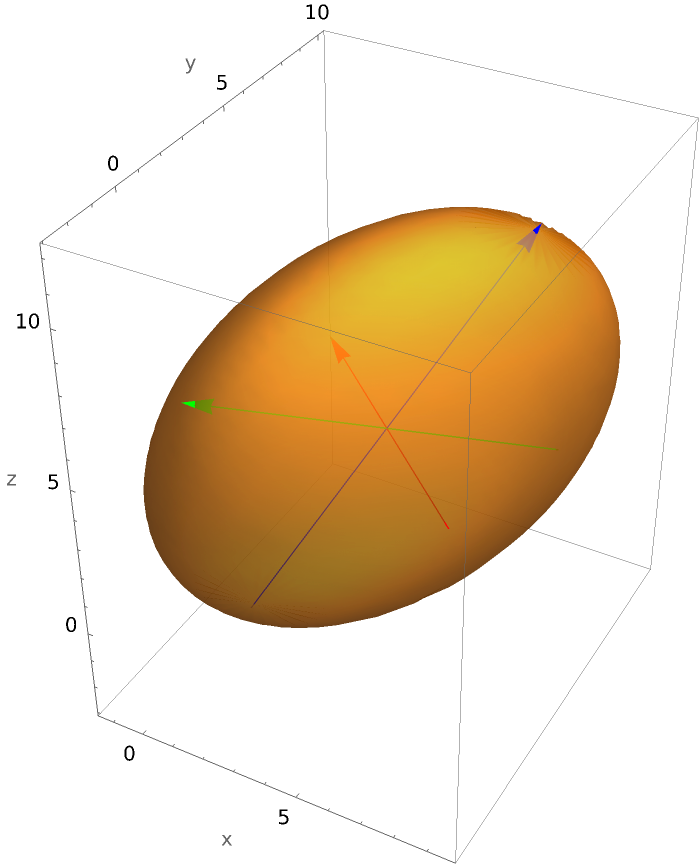 |
Use formal variables:
| In[11]:= |
| Out[11]= |
Nine random real points:
| In[12]:= |
| Out[12]= |  |
The quadric through these points:
| In[13]:= |
| Out[13]= |
Show the quadric surface (a hyperboloid of 2 sheets) with the points:
| In[14]:= | ![Graphics3D[{ContourPlot3D[
quadric == 0, {x, -4, 4}, {y, -4, 4}, {z, -4, 4}, ContourStyle -> Opacity[0.3]][[1]], {ColorData[97, 4], Sphere[pts, Scaled[0.008]]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/b83/b83b1231-6125-424e-8249-c375abfd87fd/6556de2370fe8ef3.png) |
| Out[14]= | 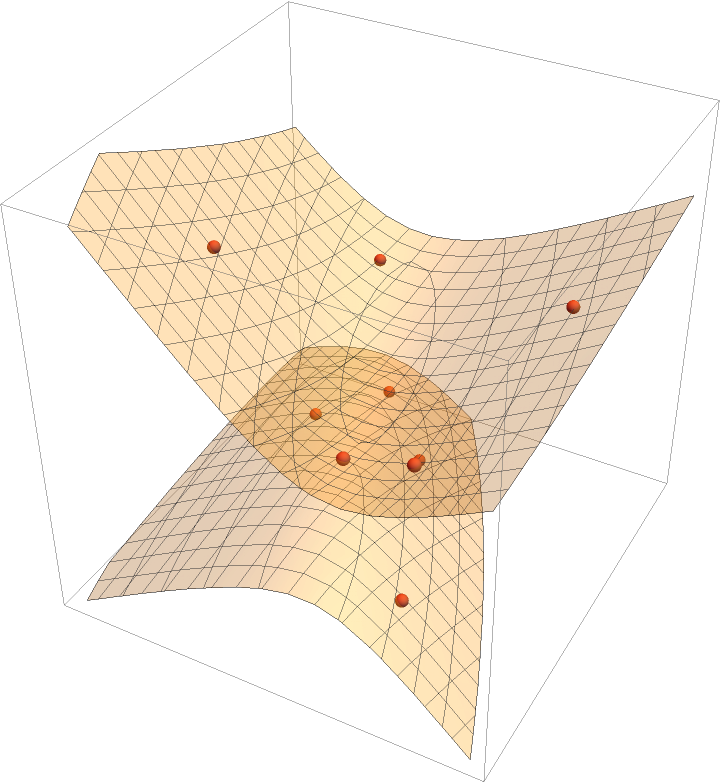 |
Pick nine points on a sphere:
| In[15]:= |
| Out[15]= |
Find the surface of the sphere:
| In[16]:= |
| Out[16]= |
The following set of nine points should give the same sphere equation, but the matrix method fails due to degeneracy:
| In[17]:= |
| Out[17]= |
This work is licensed under a Creative Commons Attribution 4.0 International License