Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 BiasedRescale

Source Notebook

Bias a value in the unit interval either lower or higher

Contributed by: Jan Mangaldan

ResourceFunction["BiasedRescale"][a,x]

biases x toward lower values if a<1/2 and toward higher values if a>1/2 as x runs from 0 to 1.

ResourceFunction["BiasedRescale"][a,x,{min,max}]

biases x as x runs from min to max.

ResourceFunction["BiasedRescale"][a,x,{min,max},{ymin,ymax}]

biases x as x runs from min to max, with the result rescaled to run from ymin to ymax.

Details and Options

a can be any real number between 0 and 1.
The result of ResourceFunction["BiasedRescale"][a,x,{min,max}] is always between 0 and 1.
ResourceFunction["BiasedRescale"] can take the Method option for the bias function to use.
Possible settings for the Method option are "Schlick" (default) and "Perlin".
With the default option setting Method→"Schlick", ResourceFunction["BiasedRescale"] uses Schlick's bias function x/((1/a-2)(1-x)+1).
With Method→"Perlin", ResourceFunction["BiasedRescale"] uses Perlin's bias function x-log2(a).
ResourceFunction["BiasedRescale"] is commonly used in computer graphics.

Examples

Basic Examples (3) 

Evaluate numerically:

In[1]:=
ResourceFunction["BiasedRescale"][1/8, 0.6]
Out[1]=

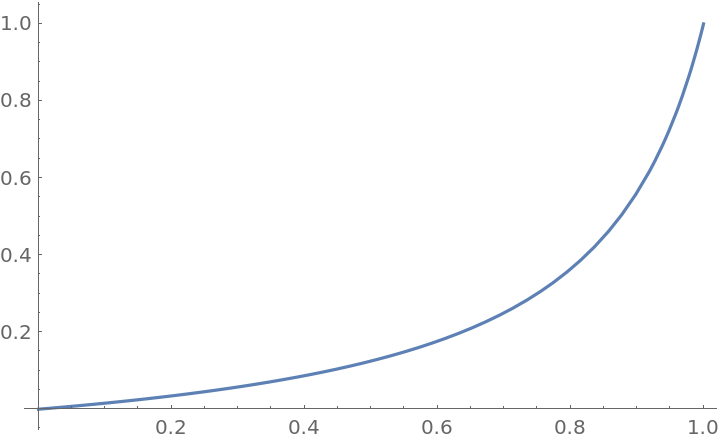
Plot over a subset of the reals:

In[2]:=
Plot[ResourceFunction["BiasedRescale"][1/8, x], {x, 0, 1}]
Out[2]=

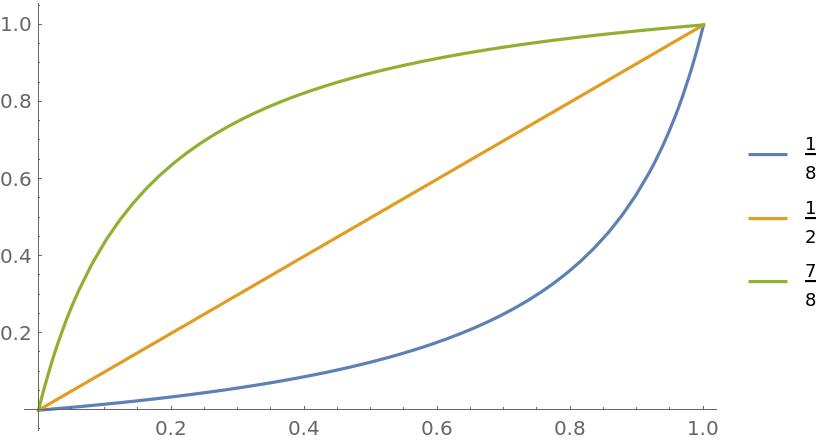
Plot different bias functions:

In[3]:=
Plot[Evaluate@ Table[ResourceFunction["BiasedRescale"][a, x], {a, {1/8, 1/2, 7/8}}], {x, 0, 1}, PlotLegends -> {1/8, 1/2, 7/8}]
Out[3]=

Scope (4) 

Evaluate for symbolic x:

In[4]:=
ResourceFunction["BiasedRescale"][1/4, x]
Out[4]=

BiasedRescale threads over lists in its first and second arguments:

In[5]:=
ResourceFunction["BiasedRescale"][{1/8, 1/2, 7/8}, 0.3]
Out[5]=
In[6]:=
ResourceFunction["BiasedRescale"][7/8, {0.1, 0.3, 0.5}]
Out[6]=

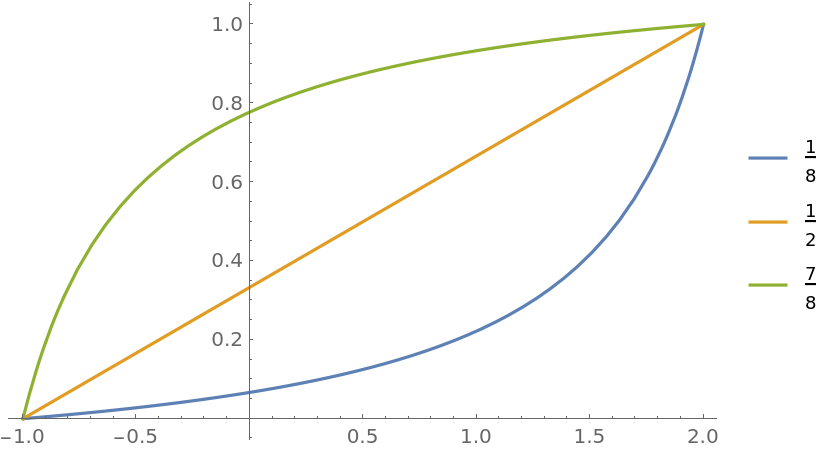
Plot different bias functions with a rescaled domain:

In[7]:=
Plot[Evaluate@ Table[ResourceFunction["BiasedRescale"][a, x, {-1, 2}], {a, {1/8, 1/2, 7/8}}], {x, -1, 2}, PlotLegends -> {1/8, 1/2, 7/8}]
Out[7]=

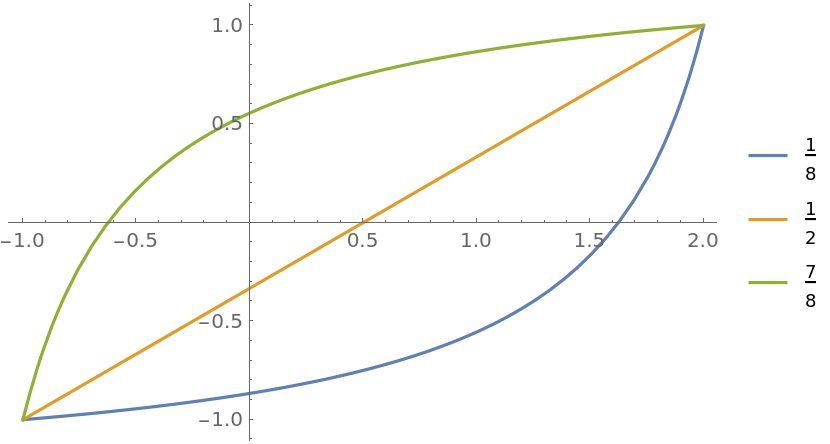
Plot different bias functions with a rescaled domain and range:

In[8]:=
Plot[Evaluate@ Table[ResourceFunction["BiasedRescale"][a, x, {-1, 2}, {-1, 1}], {a, {1/8, 1/2, 7/8}}], {x, -1, 2}, PlotLegends -> {1/8, 1/2, 7/8}]
Out[8]=

Options (1) 

Method (1) 

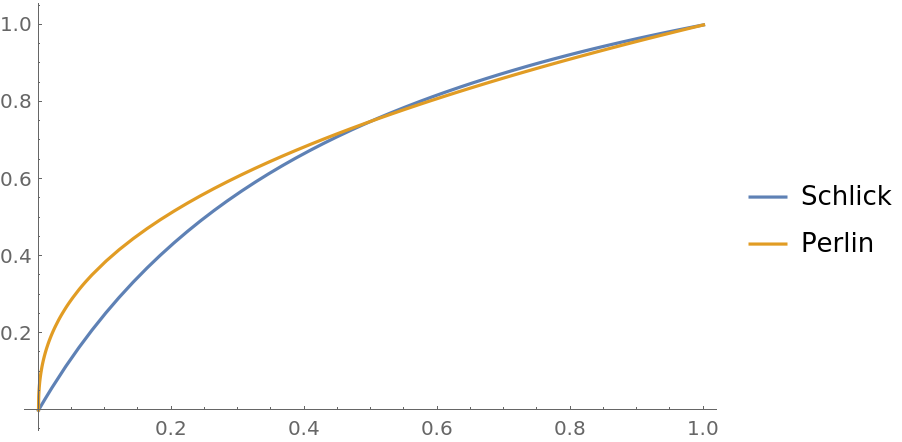
Compare the Schlick and Perlin bias functions:

In[9]:=
{ResourceFunction["BiasedRescale"][3/4, x, Method -> "Schlick"], ResourceFunction["BiasedRescale"][3/4, x, Method -> "Perlin"]}
Out[9]=
In[10]:=
Plot[{ResourceFunction["BiasedRescale"][3/4, x, Method -> "Schlick"], ResourceFunction["BiasedRescale"][3/4, x, Method -> "Perlin"]}, {x, 0, 1}, PlotLegends -> {"Schlick", "Perlin"}]
Out[10]=

Applications (2) 

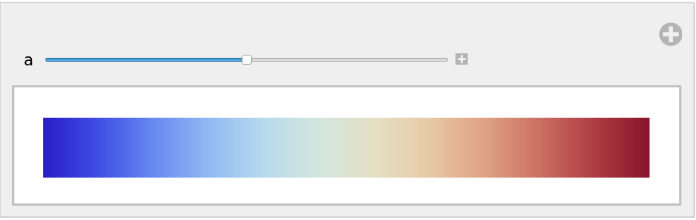
Adjust the middle color of a built-in color gradient:

In[11]:=
Manipulate[ LinearGradientImage[ ColorData["ThermometerColors", ResourceFunction["BiasedRescale"][a, #]] &, {300, 30}], {{a, 1/2}, 0, 1}]
Out[11]=

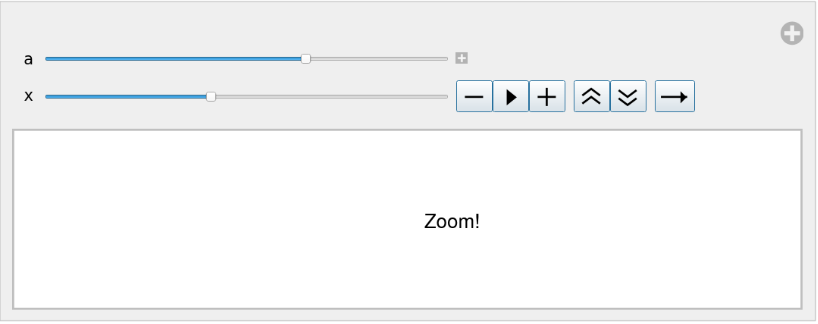
Demonstrate the effect of BiasedRescale on easing in/easing out:

In[12]:=
Manipulate[ Graphics[Text[ "Zoom!", {ResourceFunction["BiasedRescale"][a, x, {-1, 2}], 0}], PlotRange -> {{-0.1, 1.1}, {-0.1, 0.1}}], {{a, 1/2}, 0, 1}, {x, -1, 2, ControlType -> Animator, AnimationRunning -> False}]
Out[12]=

Properties and Relations (1) 

BiasedRescale[1/2,x,{min,max}] is equivalent to Rescale[x,{min,max}]:

In[13]:=
ResourceFunction["BiasedRescale"][1/2, x, {a, b}] == Rescale[x, {a, b}] // Simplify
Out[13]=

Possible Issues (2) 

BiasedRescale is left unevaluated if the first argument is non-numeric:

In[14]:=
ResourceFunction["BiasedRescale"][a, x]
Out[14]=

BiasedRescale is left unevaluated if the first argument is not a real number between 0 and 1:

In[15]:=
ResourceFunction["BiasedRescale"][-1, x]
Out[15]=

Neat Examples (6) 

Use BiasedRescale with the resource function GaussianQuadratureWeights to evaluate a Cauchy principal value integral.

The function to be integrated and the integration limits:

In[16]:=
f[x_] := E^x/x; xmin = -1.; xmax = 3.;

Even-order Gaussian quadrature abscissas and weights:

In[17]:=
{ab, wt} = Transpose[ ResourceFunction["GaussianQuadratureWeights"][20, {xmin, xmax}]];

The transformation function to be applied to the abscissas and weights:

In[18]:=
tr[x_] = ResourceFunction["BiasedRescale"][Rescale[0, {xmin, xmax}], x, {xmin, xmax}, {xmin, xmax}];

Transform the abscissas and weights:

In[19]:=
wt *= tr'[ab]
Out[19]=
In[20]:=
ab = tr[ab]
Out[20]=

Compute the integral:

In[21]:=
res = wt . f[ab]
Out[21]=

Compare with the result of NIntegrate:

In[22]:=
% - NIntegrate[f[x], {x, xmin, 0, xmax}, Method -> "PrincipalValue"]
Out[22]=

Version History

  • 1.0.1 – 16 February 2021
  • 1.0.0 – 28 December 2020

Source Metadata

  • Citation:
    • Perlin K., Hoffert E.M., Hypertexture. SIGGRAPH ‘89: Proceedings of the 16th annual conference on Computer graphics and interactive techniques, 253-262, 1989 DOI: 10.1145/74333.74359
    • Schlick C., Fast alternatives to Perlin’s bias and gain functions. Graphics Gems IV, 401-403, 1994 DOI: 10.1016/B978-0-12-336156-1.50050-1

Related Resources

License Information