Function Repository Resource:

FunctionMonotonicity

Source Notebook

Compute the regions on which an expression is monotonic

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["FunctionMonotonicity"][f,x]

returns an association of information about where f is increasing, decreasing or constant with respect to x.

ResourceFunction["FunctionMonotonicity"][f,x,property]

returns a specific property related to whether f is increasing, decreasing or constant with respect to x.

Details

ResourceFunction["FunctionMonotonicity"] expects f to be a univariate expression in terms of x, similar to what might be entered into Plot.

ResourceFunction["FunctionMonotonicity"] returns regions on which f is strictly monotonic—that is, f is strictly increasing on an interval A if for all {x,y}∈A such that x<y, it is the case that f[x]<f[y].

The input property can be any of All, "Increasing", "Decreasing", "Constant", "Regions", "Plot" or "NumberLine", and defaults to "Regions".

Examples

Basic Examples (2)

Compute the regions on which a curve is increasing, decreasing and constant:

In[1]:=

Out[1]=

Show plots as well as the regions:

In[2]:=

Out[2]=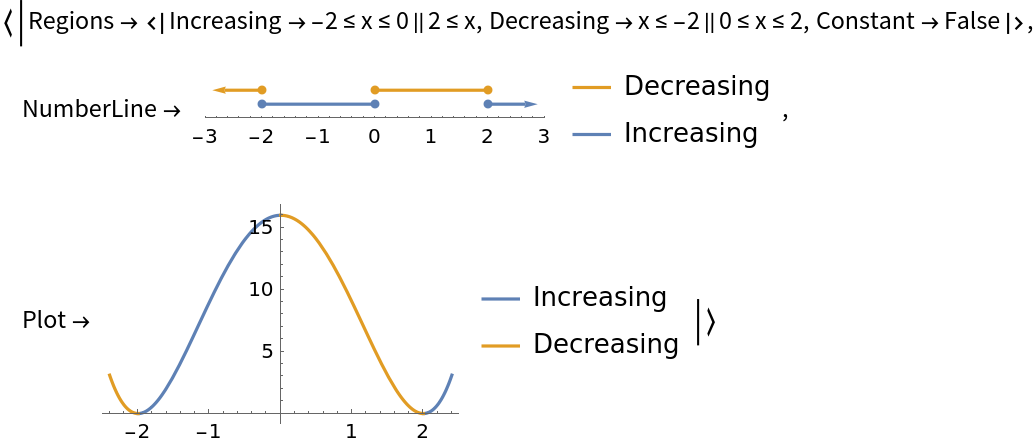

Scope (3)

FunctionMonotonicity returns strict regions of increasing and decreasing, as can be seen in this piecewise expression:

In[3]:=

In[4]:=

Out[4]=

In[5]:=

Out[5]=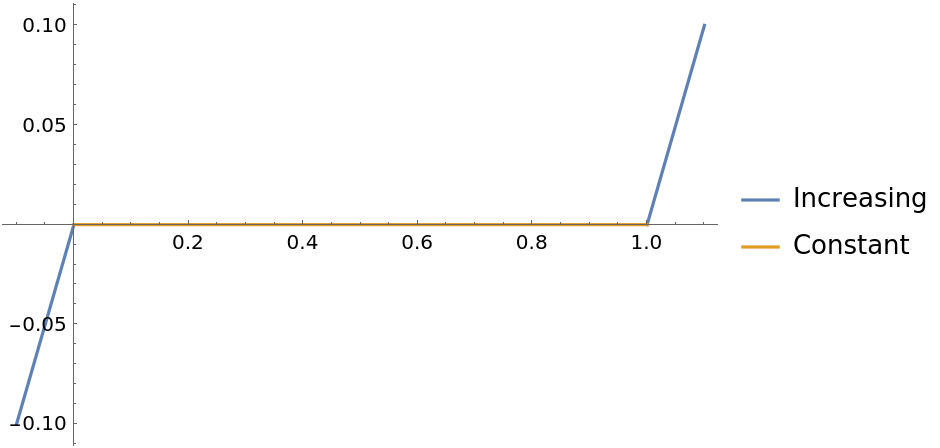

Return the "NumberLine" property to visualize the regions directly:

In[6]:=

Out[6]=

Or return the "Plot" property to visualize the regions on the plot of the curve:

In[7]:=

Out[7]=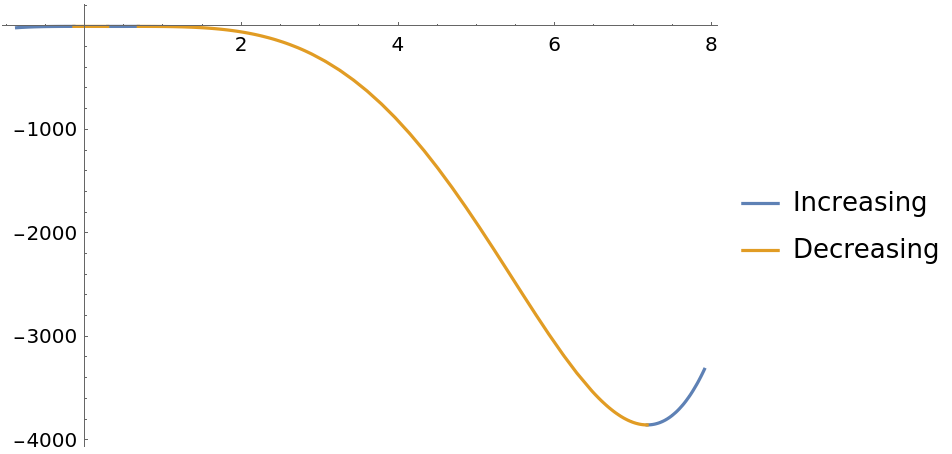

Note that a curve can be both increasing and decreasing at a given point:

In[8]:=

Out[8]=

In this case, 0 is a member of both the increasing and decreasing regions. To test that this is true against the definition of a curve being strictly increasing for x≥0, use Resolve:

In[9]:=

$Resolve[ForAll[{x, y}, {x, y} \[Element] Reals && x >= 0 && y >= 0, Implies[x < y, x^2 < y^2]]]$