Details
ResourceFunction["ToDirectedAcyclicGraph"] enables not only finding shortest paths, but also counting how many such paths exist.
ResourceFunction["ToDirectedAcyclicGraph"] takes the same options as
Graph, with the additional option "ConflictedEdges" that specifies how to handle conflicted edges.
At time t=0 the algorithm starts to expand directed edges from an initial vertex or set of vertices.
Per increment of time t, more vertices and edges are recursively added on a growing front.
Eventually, this growth process assigns a turn-on time t to each vertex, which is also its graph distance either to vertex or to one or more of the vertices.
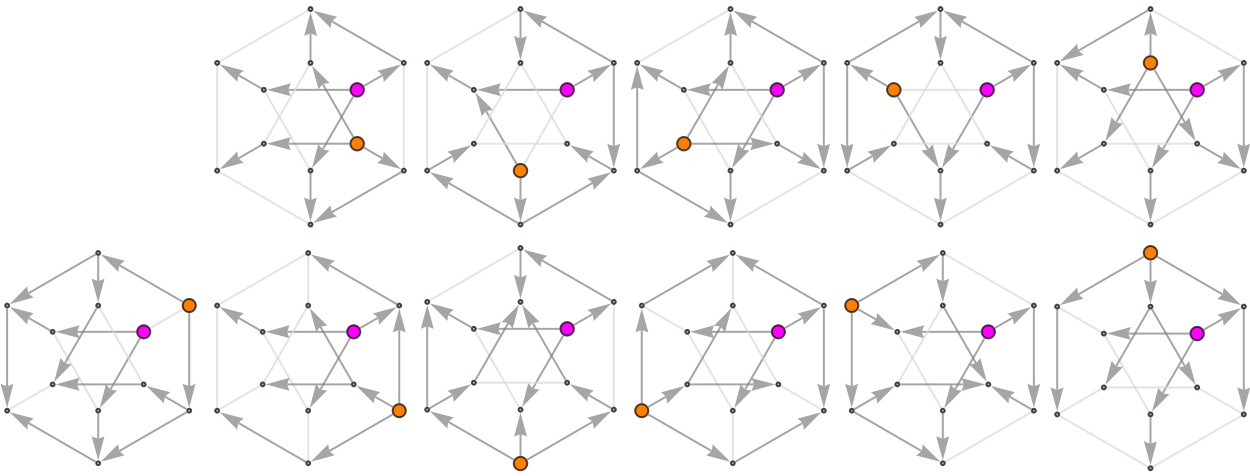
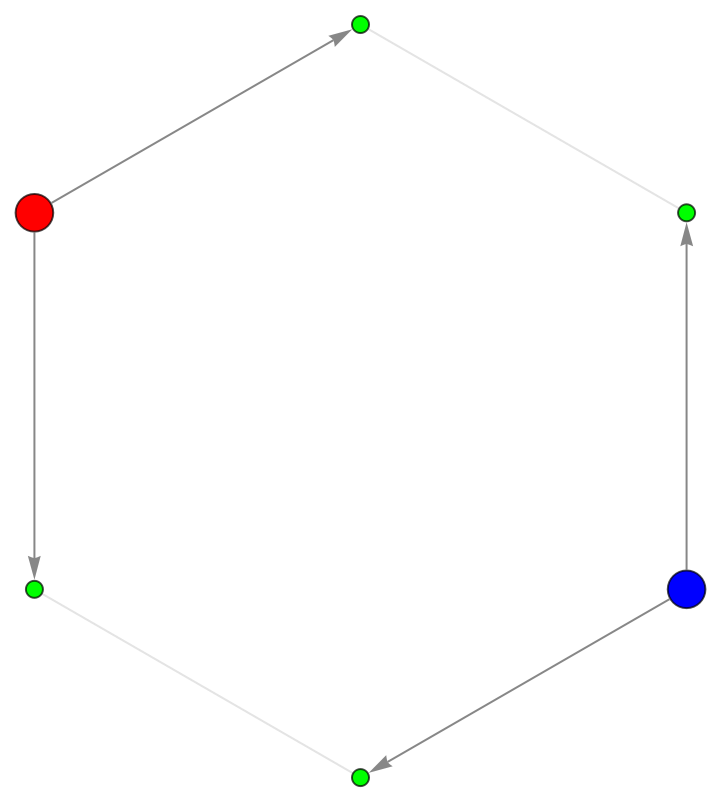
An edge is considered to be conflicted at time t if it goes between two vertices with the same turn-on time t.
With
"ConflictedEdges"→False,
ResourceFunction["ToDirectedAcyclicGraph"] deletes conflicted edges.
With
"ConflictedEdges"→True,
ResourceFunction["ToDirectedAcyclicGraph"] returns conflicted edges as undirected edges.
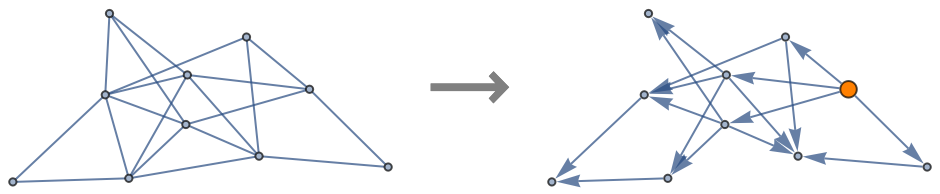
![With[{g1 = (SeedRandom["SimpleTest"]; RandomGraph[{6, 12}, ImageSize -> 200])},
Row[{g1, Style["\[LongRightArrow]", 32, Gray, Bold], ResourceFunction["ToDirectedAcyclicGraph"][g1, 1,
VertexStyle -> {1 -> Orange}, VertexSize -> {1 -> 1/3}, ImageSize -> 200]},
Spacer[10]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/1-0-0/3206af90c60457f3.png)
![With[{g1 = (SeedRandom["SimpleTest"]; RandomGraph[{10, 20}, ImageSize -> 200])},
And[AcyclicGraphQ[#], DirectedGraphQ[#]] &@
ResourceFunction["ToDirectedAcyclicGraph"][g1, 1]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/1-0-0/48c404f67286af6f.png)
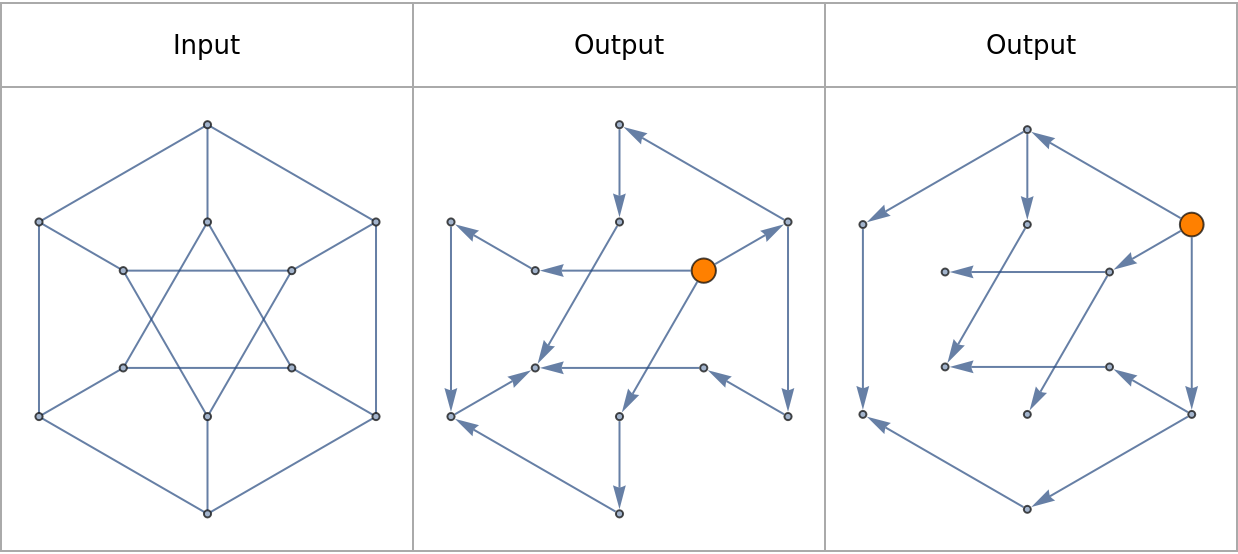
![Grid[{Text /@ {"Input", "Output", "Output"},
Prepend[
ResourceFunction["ToDirectedAcyclicGraph"][PetersenGraph[6, 2], #,
VertexStyle -> {# -> Orange}, VertexSize -> {# -> 1/4}] & /@ {1,
7},
PetersenGraph[6, 2]]}, Frame -> All, FrameStyle -> Lighter[Gray],
Spacings -> {2, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/1-0-0/7a125a84b9b62cd8.png)
![Grid[Partition[Show[#, ImageSize -> 100] & /@ ReplacePart[Map[
ResourceFunction["ToDirectedAcyclicGraph"][
PetersenGraph[6, 2], {1, #},
VertexStyle -> {1 -> Magenta, # -> Orange},
VertexSize -> {1 -> 1/4, # -> 1/4},
"ConflictedEdges" -> True,
EdgeStyle -> {UndirectedEdge[_, _] -> LightGray,
DirectedEdge[_, _] -> Gray}] &, Range[12]],
{1 -> Graph[{}]}], 6]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/1-0-0/0d395a3611e4e6db.png)
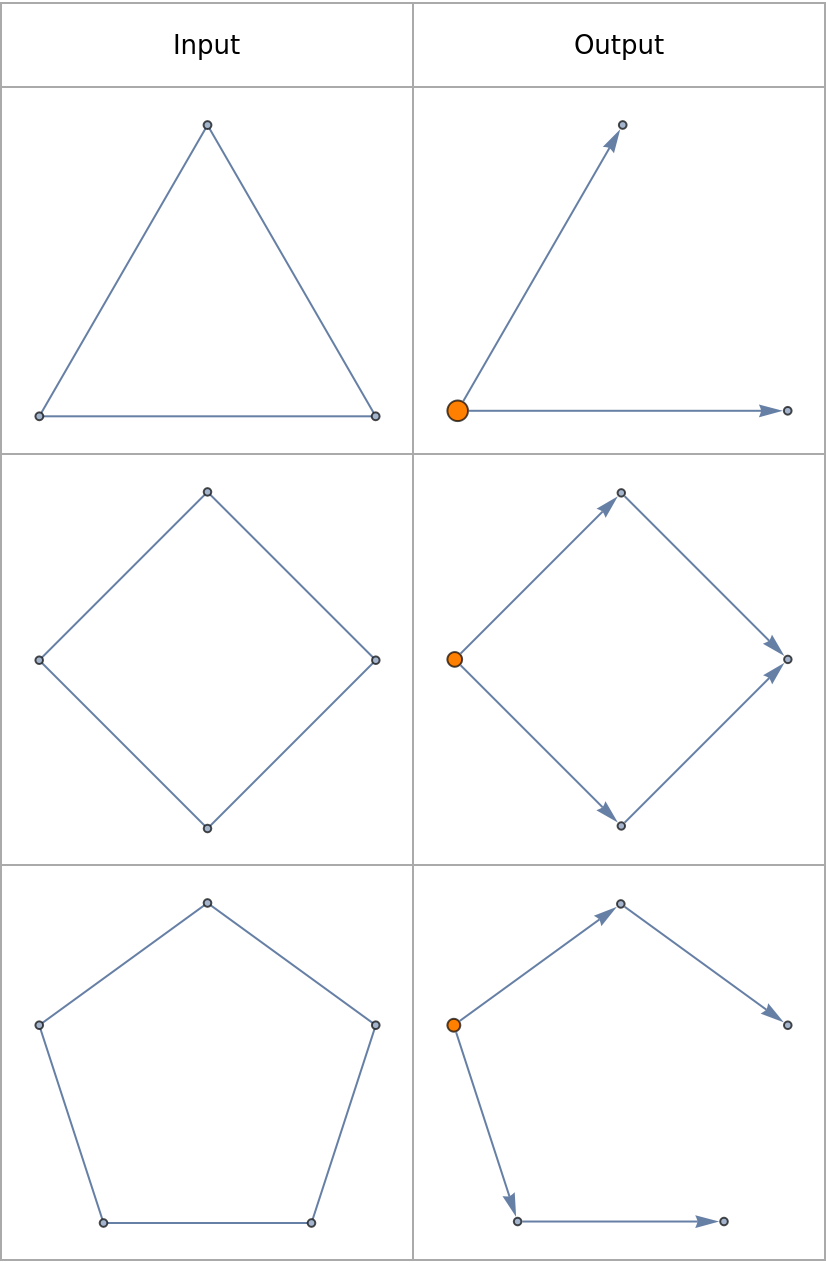
![Grid[Prepend[{CycleGraph[#],
ResourceFunction["ToDirectedAcyclicGraph"][CycleGraph[#], 1,
VertexStyle -> {1 -> Orange}, VertexSize -> {1 -> 1/16}]} & /@ {3, 4, 5},
Text /@ {"Input", "Output"}], Frame -> All,
FrameStyle -> Lighter[Gray], Spacings -> {2, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/1-0-0/1069637222b74326.png)
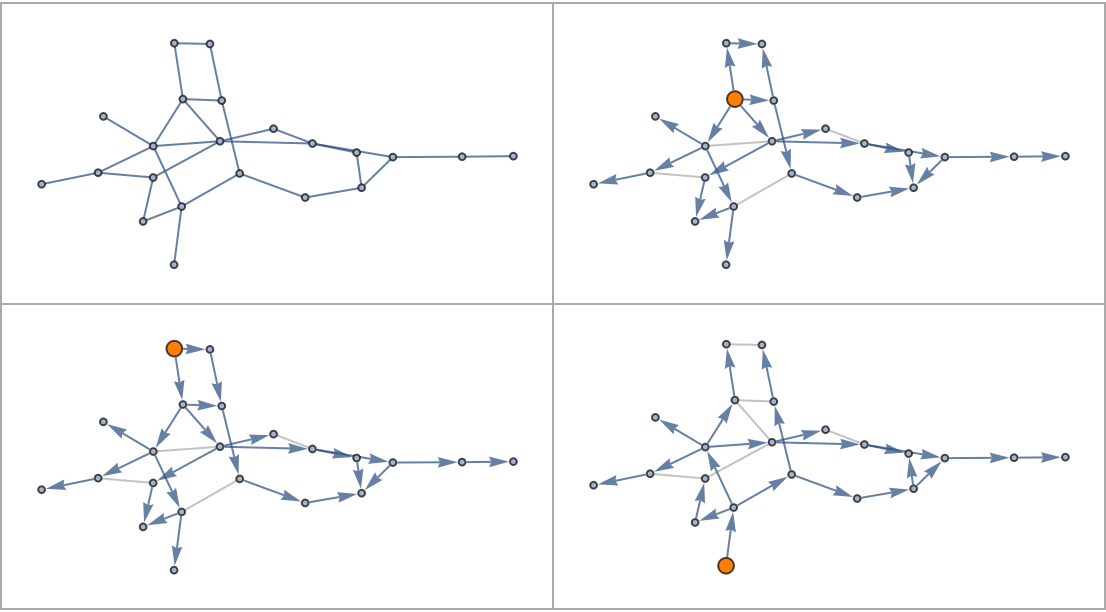
![With[{graph0 = Last[SortBy[
ConnectedGraphComponents[
SeedRandom["GraphTest"];
RandomGraph[{30, 30}]],
VertexCount]]}, Grid[Partition[
Show[#, ImageSize -> 250] & /@ Prepend[
ResourceFunction["ToDirectedAcyclicGraph"][graph0, #,
VertexStyle -> {# -> Orange},
VertexSize -> {# -> 1/2},
"ConflictedEdges" -> True,
EdgeStyle -> {UndirectedEdge[_, _] -> Lighter@Gray,
DirectedEdge[_, _] -> Arrowheads[1/25]}
] &@# & /@ RandomSample[
VertexList[graph0]][[{1, 3, 5}]],
graph0], 2], Frame -> All,
FrameStyle -> Lighter[Gray],
Spacings -> {2, 2}]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/1-0-0/33fdc130971a90de.png)
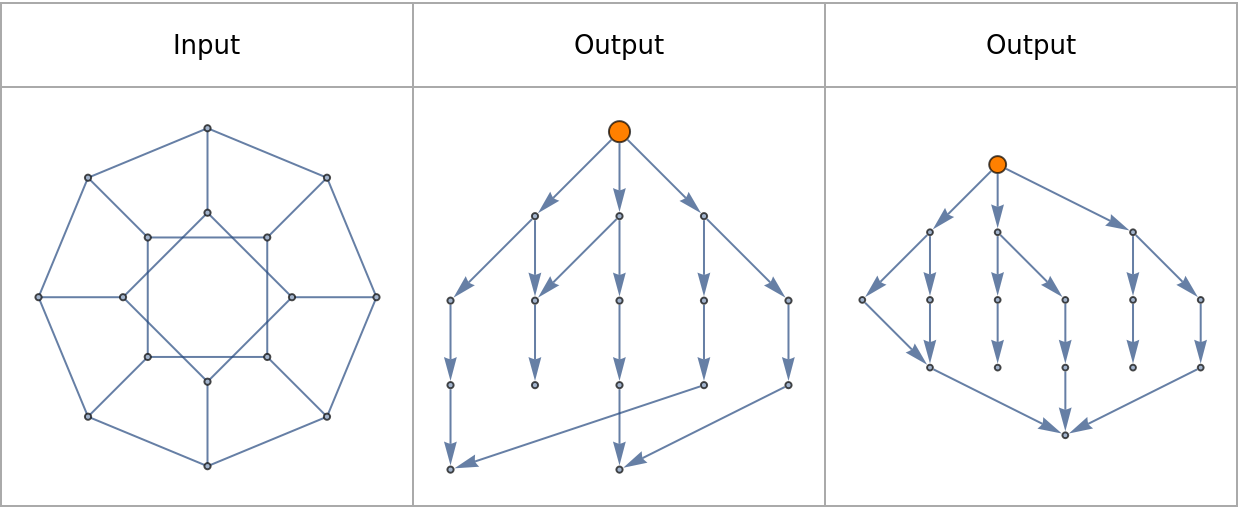
![Grid[{Text /@ {"Input", "Output", "Output"},
Prepend[
ResourceFunction["ToDirectedAcyclicGraph"][PetersenGraph[8, 2], #,
VertexStyle -> {# -> Orange}, VertexSize -> {# -> 1/4},
VertexCoordinates -> Automatic
] & /@ {1, 9}, PetersenGraph[8, 2]]},
Frame -> All, FrameStyle -> Lighter[Gray],
Spacings -> {2, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/1-0-0/6ab1179b8b2119aa.png)
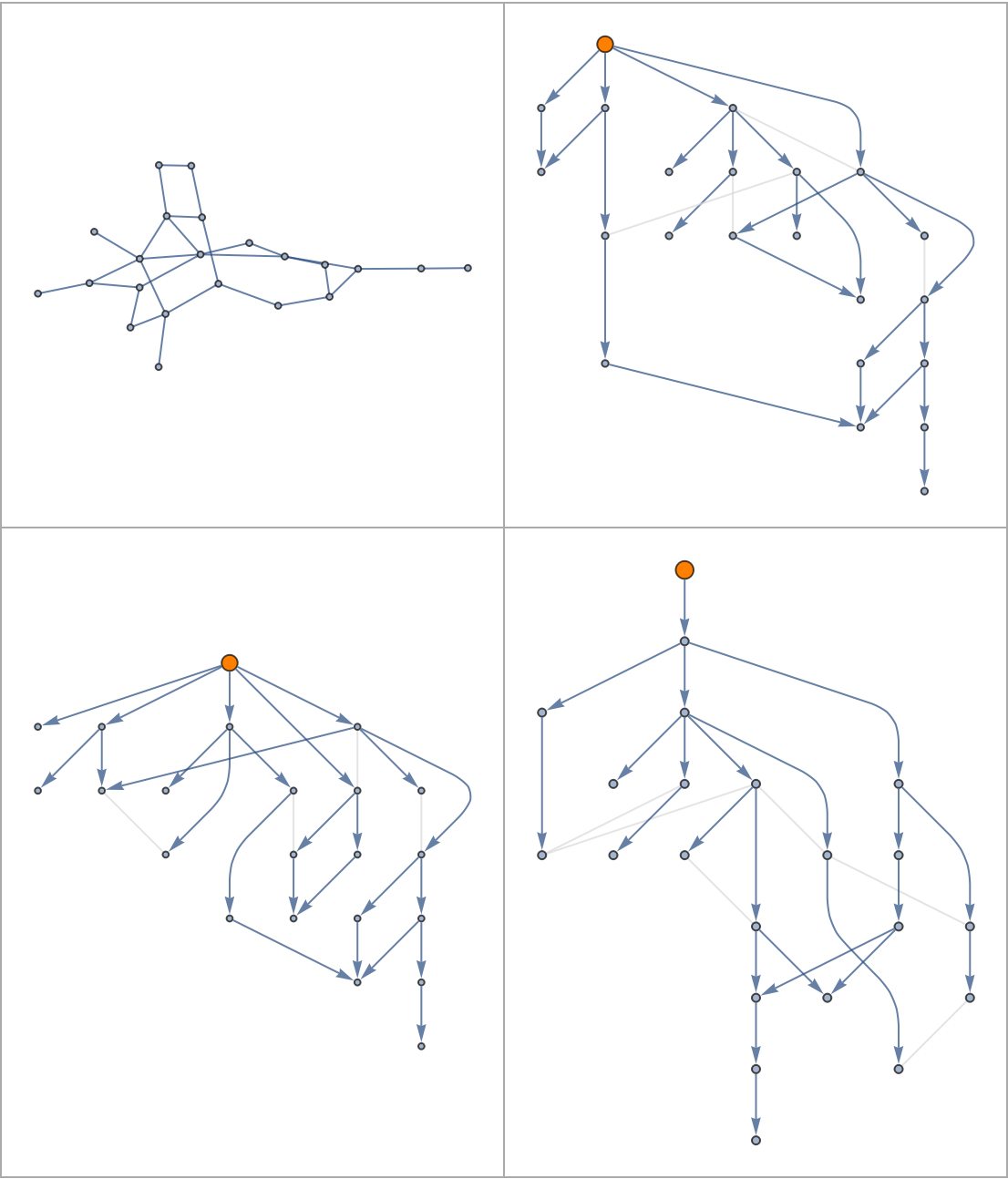
![With[{graph0 = Last[SortBy[
ConnectedGraphComponents[
SeedRandom["GraphTest"];
RandomGraph[{30, 30}]],
VertexCount]]}, Grid[Partition[
Show[#, ImageSize -> 250] & /@ Prepend[
ResourceFunction["ToDirectedAcyclicGraph"][graph0, #,
VertexStyle -> {# -> Orange},
VertexSize -> {# -> 1/4},
VertexCoordinates -> Automatic,
GraphLayout -> "LayeredDigraphEmbedding",
"ConflictedEdges" -> True,
EdgeStyle -> {UndirectedEdge[_, _] -> LightGray,
DirectedEdge[_, _] -> Arrowheads[1/25]}
] &@# & /@ RandomSample[
VertexList[graph0]][[{1, 4, 5}]],
graph0], 2], Frame -> All,
FrameStyle -> Lighter[Gray],
Spacings -> {2, 2}]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/1-0-0/4a29fdbe35362324.png)
![With[{graph0 = Last[SortBy[
ConnectedGraphComponents[RandomGraph[{30, 30}]],
VertexCount]]}, SameQ[Outer[GraphDistance[
ResourceFunction["ToDirectedAcyclicGraph"][graph0, #1], #1, #2] &,
VertexList[graph0], VertexList[graph0], 1],
GraphDistanceMatrix[graph0]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/1-0-0/26f500041be8ce96.png)
![ResourceFunction["ToDirectedAcyclicGraph"][CycleGraph[6], {1, 4},
"ConflictedEdges" -> True,
VertexStyle -> {1 -> Red, 4 -> Blue, 2 | 3 | 5 | 6 -> Green},
VertexSize -> {1 -> 1/10, 4 -> 1/10},
EdgeStyle -> {UndirectedEdge[_, _] -> LightGray,
DirectedEdge[_, _] -> Darker@Gray}]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/1-0-0/1572ac16eb99a2e5.png)
![CountWalks[graph0_, loc_] := CountWalks[graph0, loc
] = If[loc == 1, 1, Total[Cases[EdgeList[graph0],
DirectedEdge[pre_, loc
] :> CountWalks[graph0, pre]]]];](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/1-0-0/03f6dcd6a541f687.png)
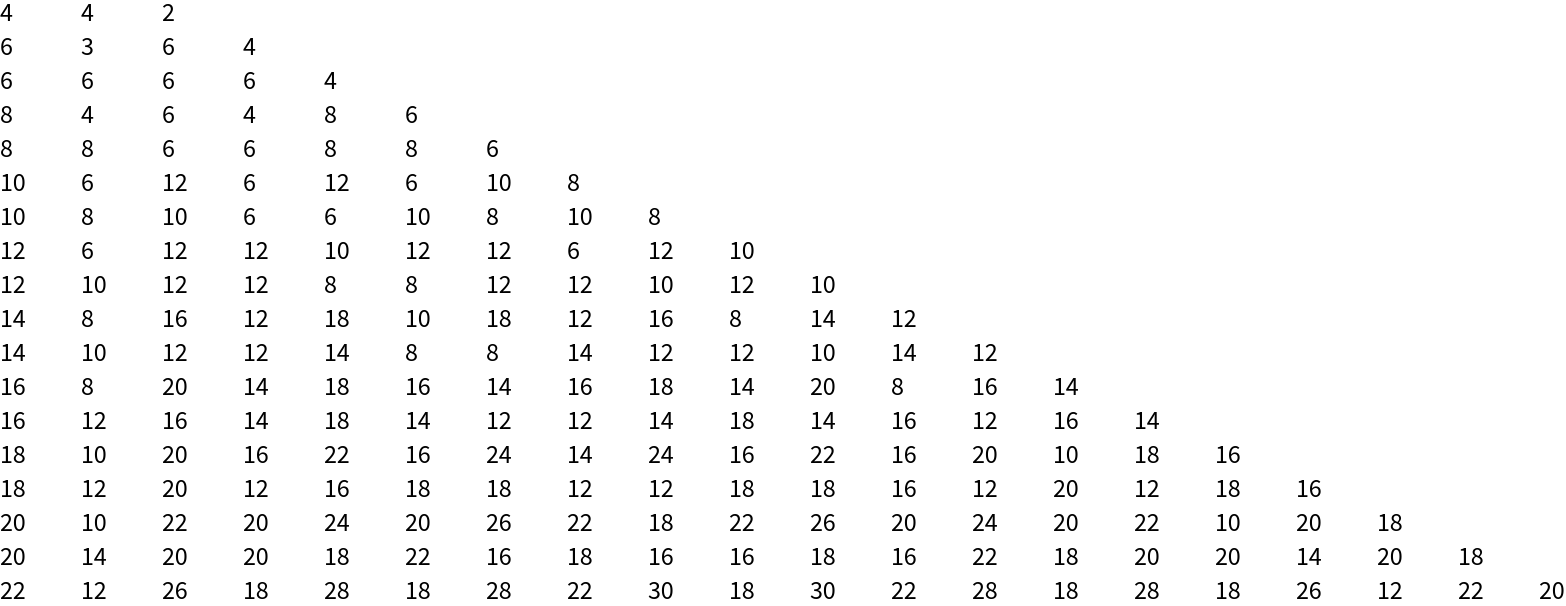
![TableForm[countWalksTable = Table[With[
{graph0 = ResourceFunction["ToDirectedAcyclicGraph"][PetersenGraph[i, j], 1]},
Total[CountWalks[graph0, #] & /@ Select[VertexList[graph0],
SameQ[Cases[EdgeList[graph0], DirectedEdge[#, _]], {}] &]]],
{i, 3, 20}, {j, 1, i}]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/1-0-0/5b70dee0e58c4f3b.png)
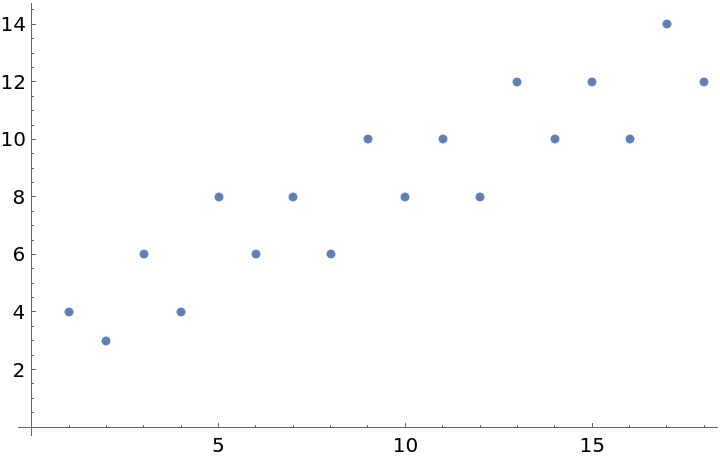
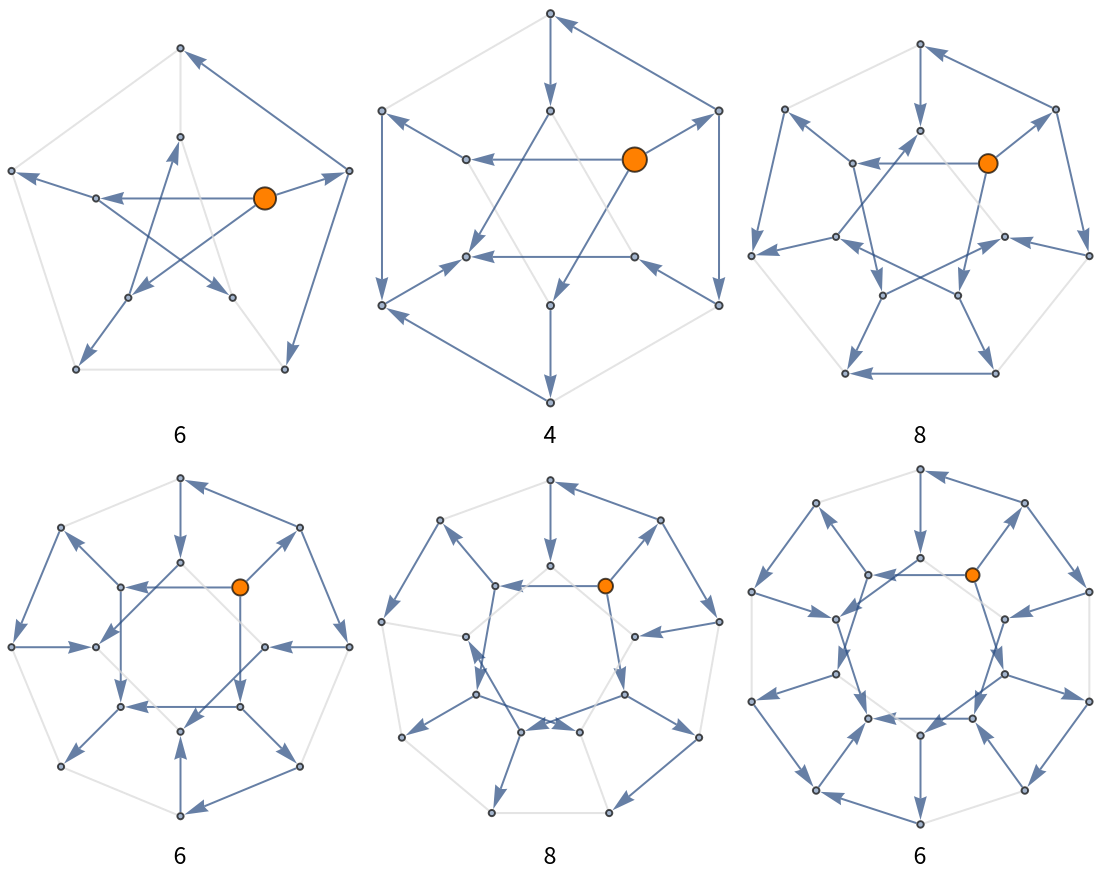
![Grid[Riffle[Partition[
ResourceFunction["ToDirectedAcyclicGraph"][PetersenGraph[#, 2], 1,
VertexStyle -> {1 -> Orange}, VertexSize -> {1 -> 1/4},
"ConflictedEdges" -> True,
EdgeStyle -> {UndirectedEdge[_, _] -> LightGray}]
& /@ Range[5, 10], 3], Partition[countWalksTable[[3 ;; 9, 2]], 3]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/1-0-0/5b435cf4f4a43d76.png)