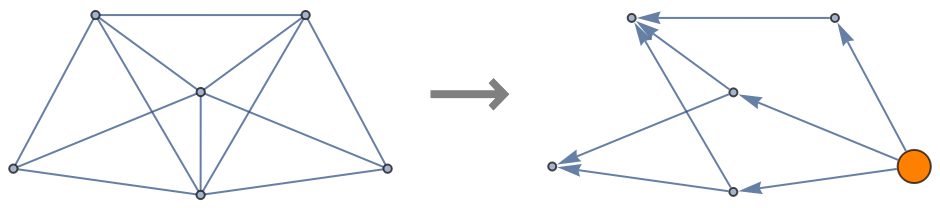
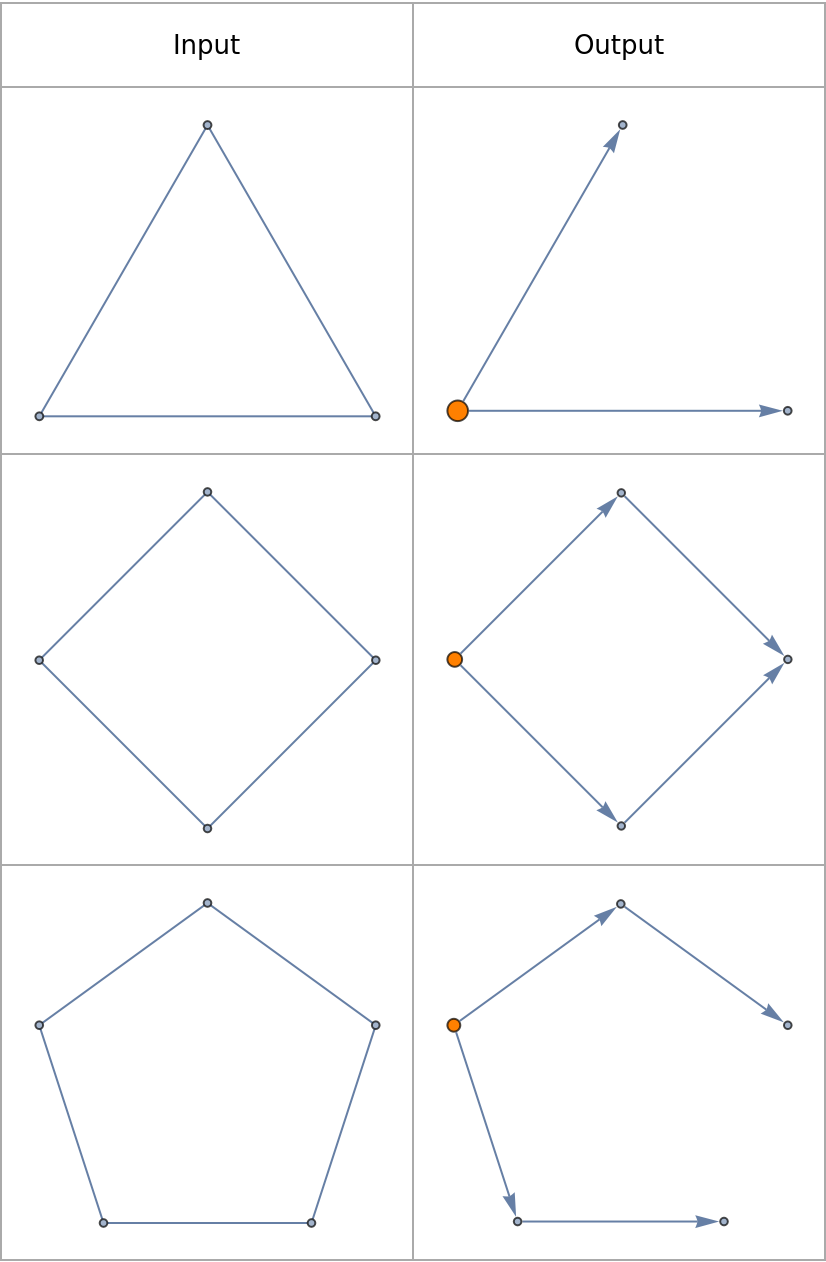
Basic Examples (2)
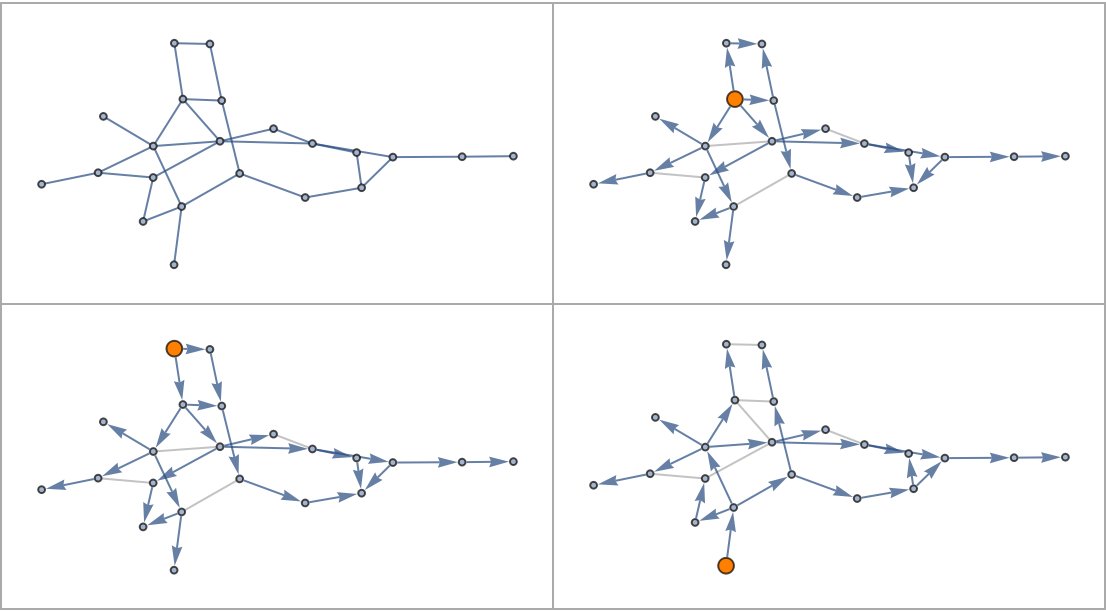
Determine all shortest paths on a random graph:
Verify that the output above is indeed directed and acyclic:
Scope (3)
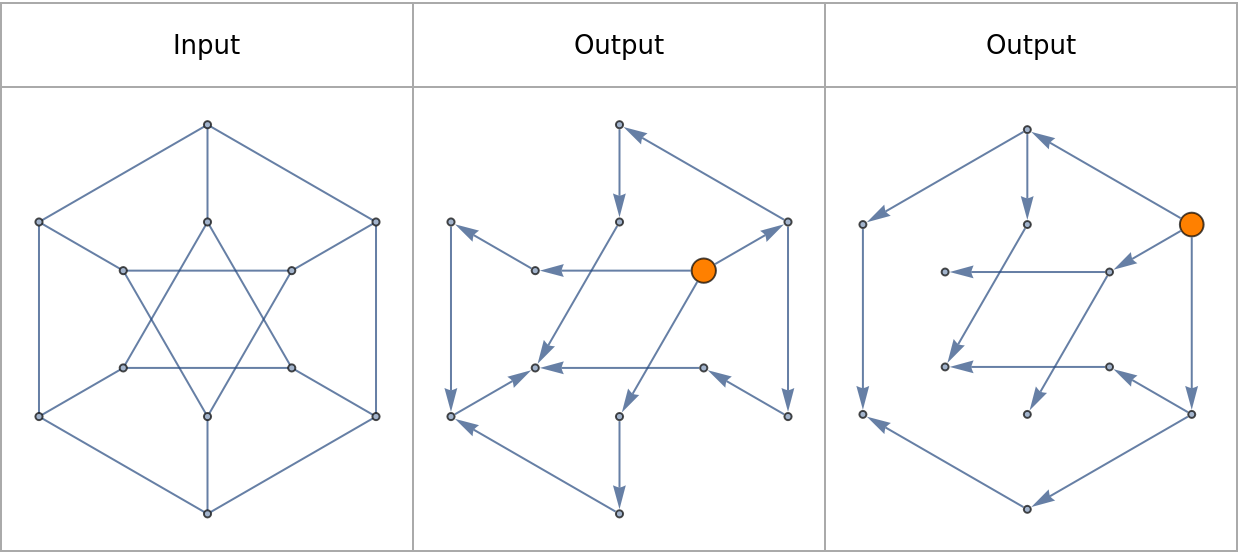
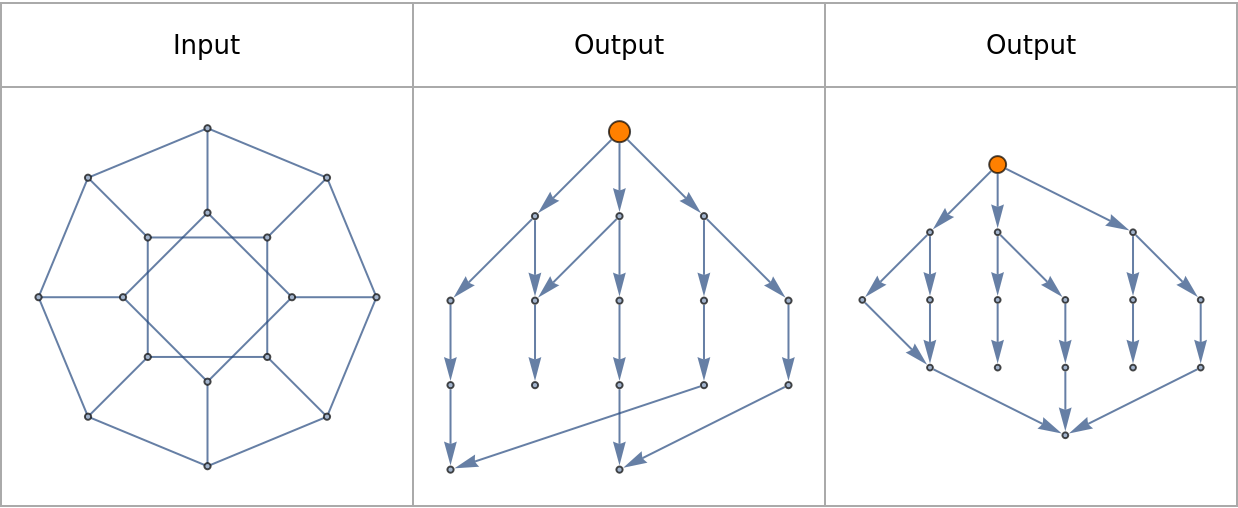
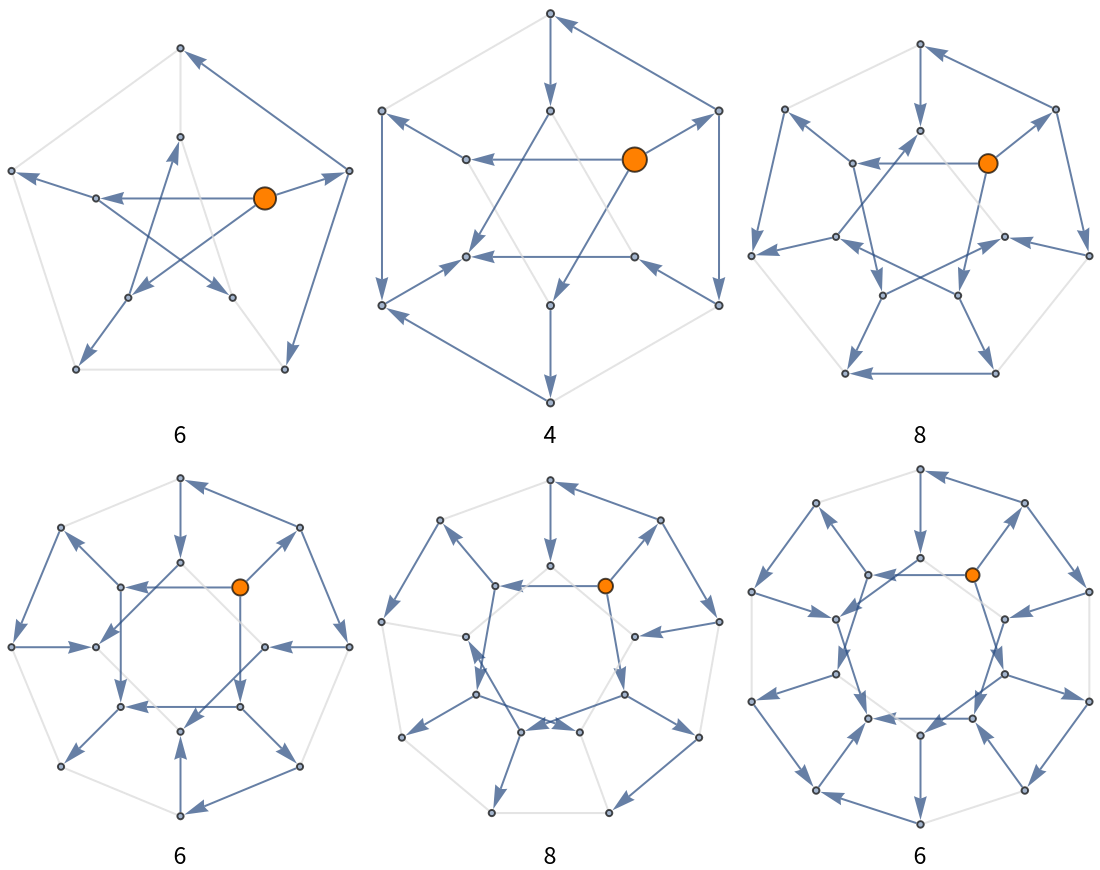
Explore traversal maps of a Petersen graph:
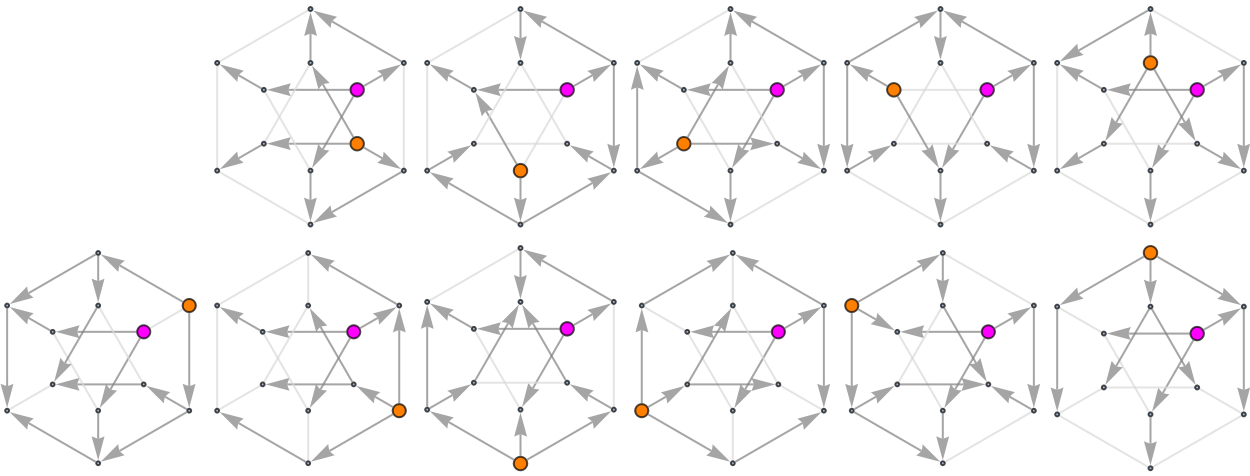
Add another Graph-exploring reference point and compare possible pairwise dance moves:
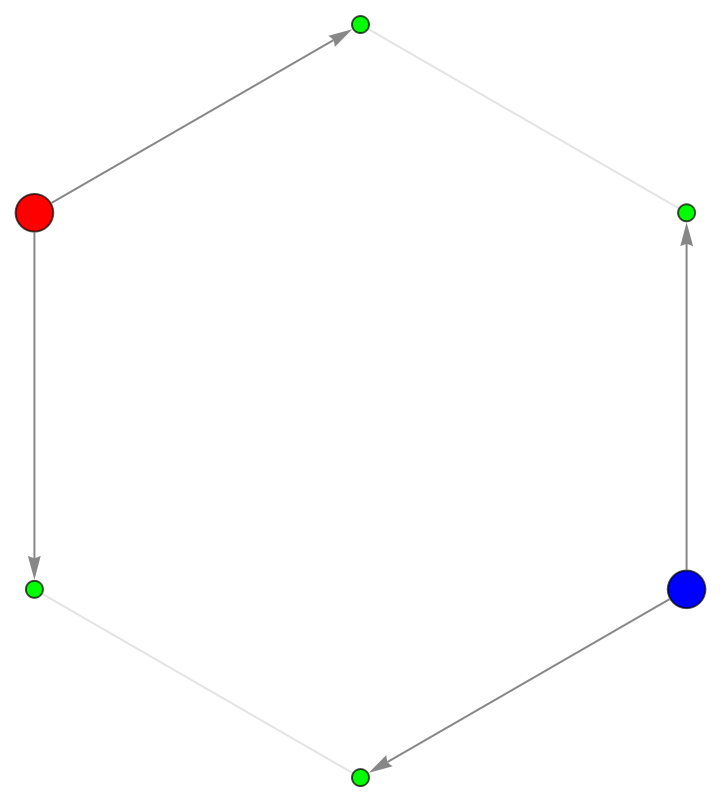
Check to see that edges are lost only on odd cycles:
Compare what happens when different initial conditions are chosen:
Options (3)
Acyclic directed graphs can be plotted as causal graphs by setting VertexCoordinates to Automatic:
Plot a few more causal graphs:
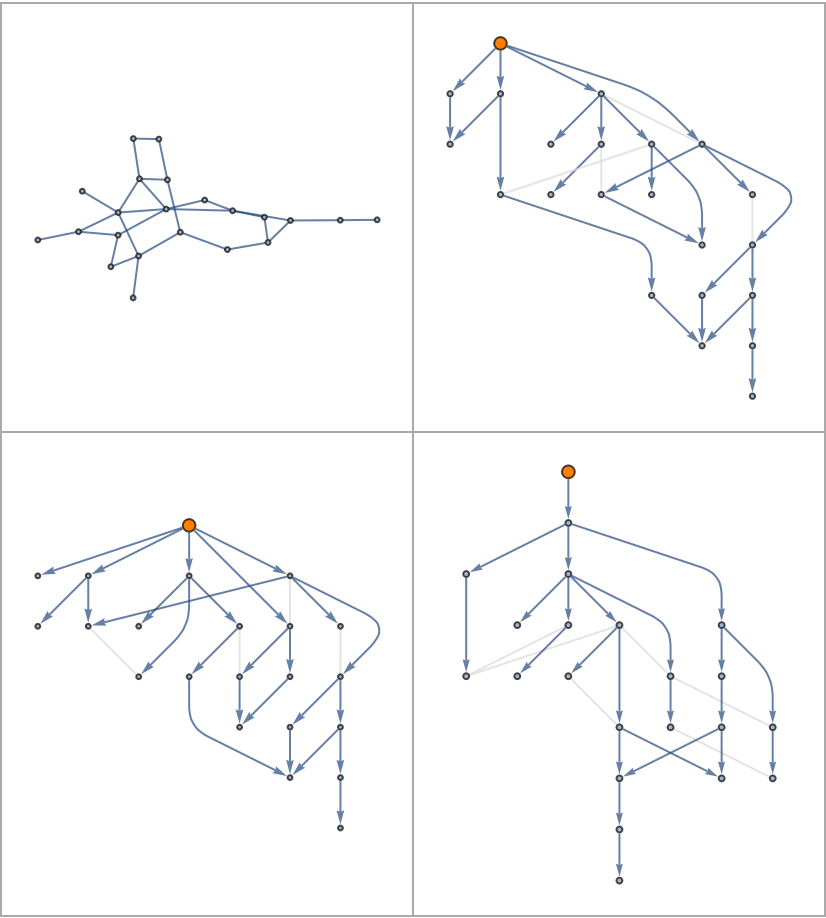
Resolve conflicted edges by specifying a CollisionFunction:
Check non-uniqueness of path lengths:
Properties and Relations (2)
The transformation acts as the identity on rows of the GraphDistanceMatrix:
Using Identity as the CollisionFunction returns the same output as DirectedGraph with "Acyclic" conversion:
Possible Issues (3)
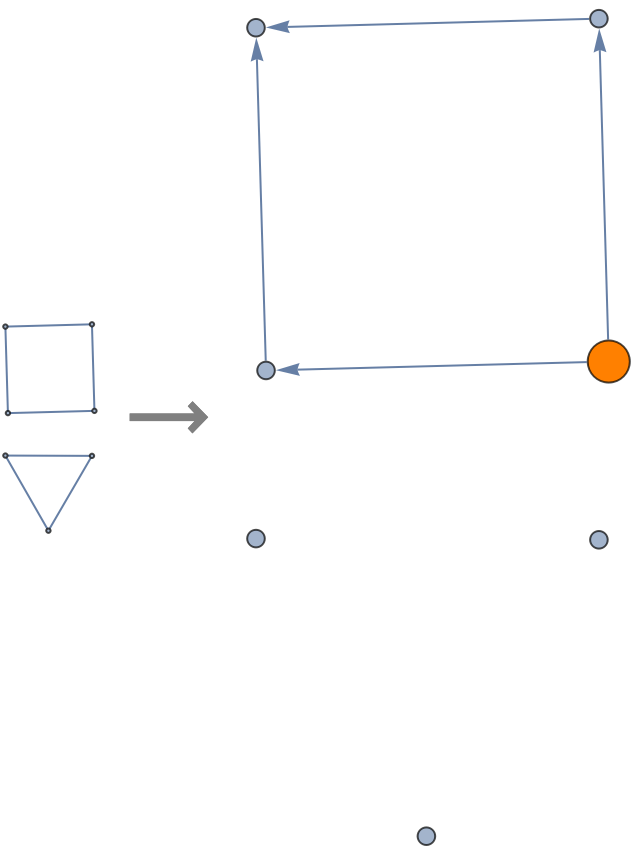
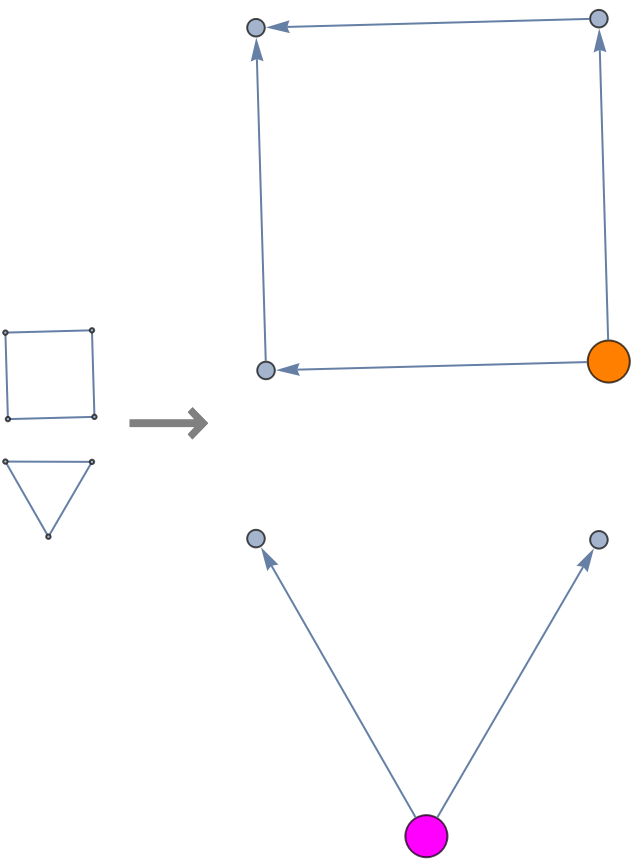
Specifying multiple reference points can divide the graph into disconnected components:
Inputs with disconnected components may return only one component:
This can be fixed by specifying initial vertices on each component:
The function will balk at nonsense inputs:
Neat Examples (2)
Count possible walks on all Petersen graph outputs:
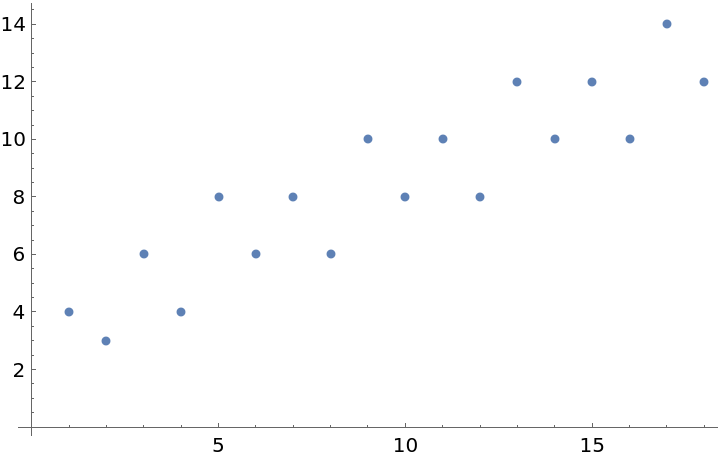
List a sequence that does not have an entry in the OEIS:
Plot the possibly new sequence:
Conjecture the form of a linear recurrence:
Compare with depictions to try and formulate a proof argument:
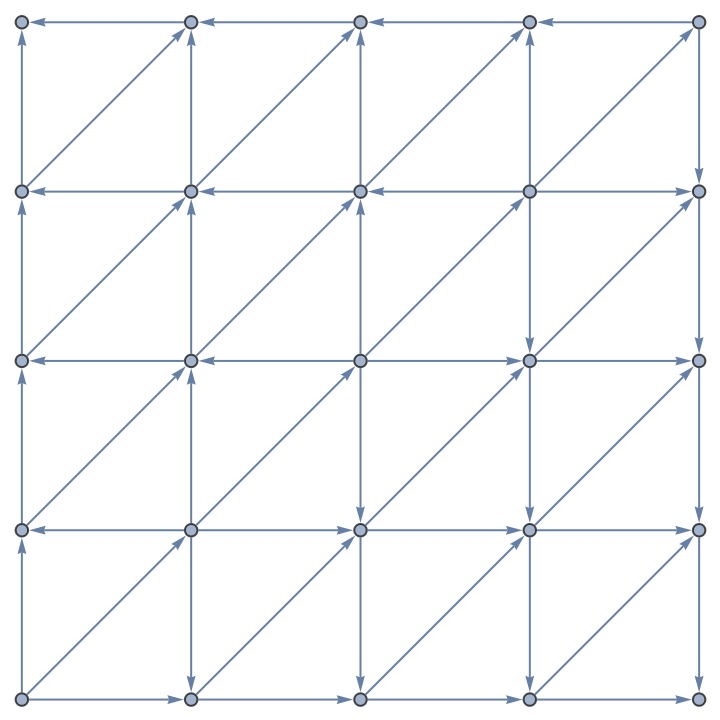
Resolve conflicted edges in a square grid:
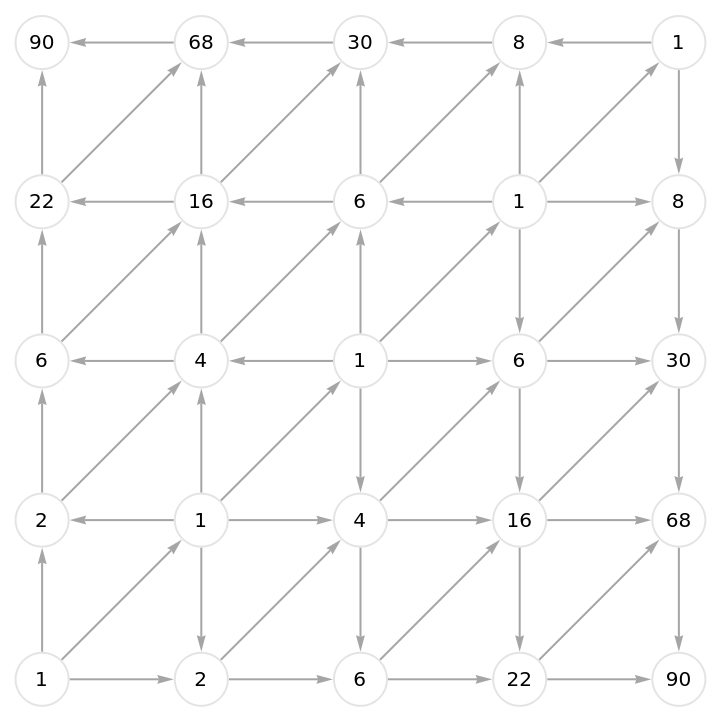
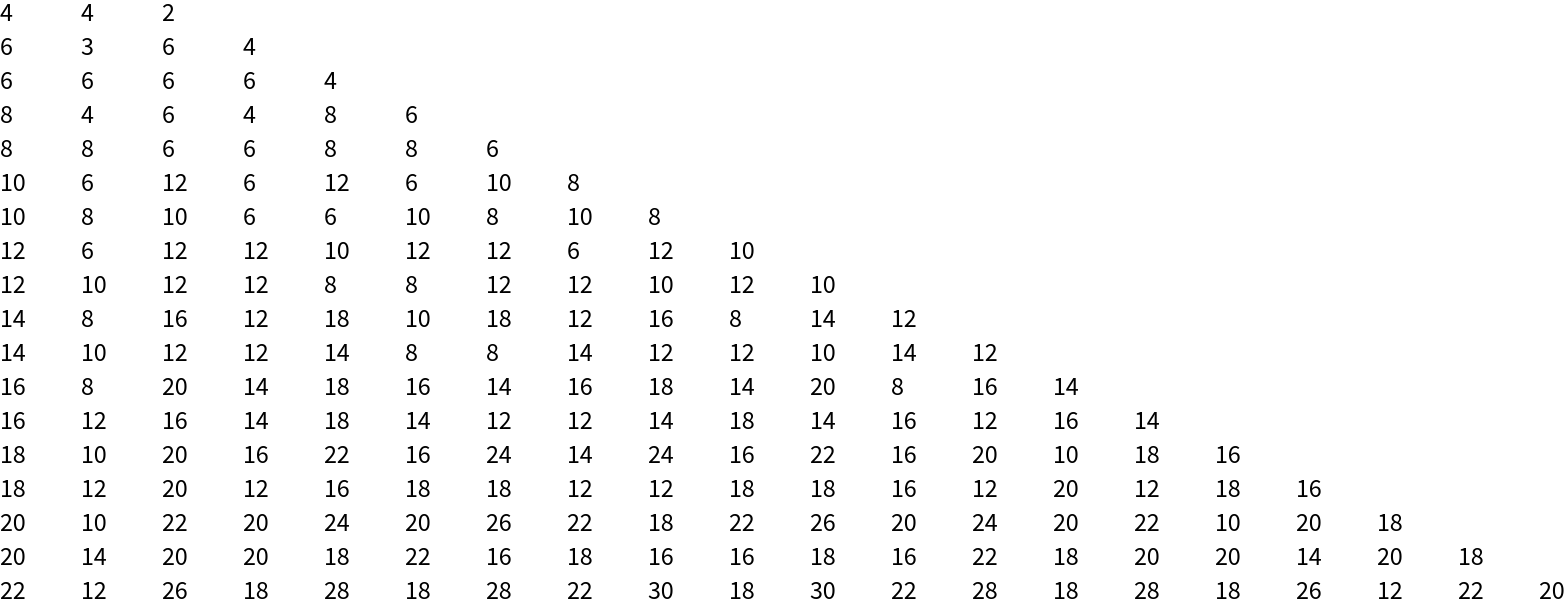
Calculate part of a numerical triangle associated with the Schroeder numbers (cf. OEIS A033877):
![With[{g1 = (SeedRandom["SimpleTest"]; RandomGraph[{6, 12}, ImageSize -> 200])},
Row[{g1, Style["\[LongRightArrow]", 32, Gray, Bold], ResourceFunction["ToDirectedAcyclicGraph"][g1, 1,
VertexStyle -> {1 -> Orange}, VertexSize -> {1 -> 1/3}, ImageSize -> 200]},
Spacer[10]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/171048c45b7efb71.png)
![With[{g1 = (SeedRandom["SimpleTest"]; RandomGraph[{10, 20}, ImageSize -> 200])},
And[AcyclicGraphQ[#], DirectedGraphQ[#]] &@
ResourceFunction["ToDirectedAcyclicGraph"][g1, 1]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/2d056a7ebdf8de61.png)
![Grid[{Text /@ {"Input", "Output", "Output"},
Prepend[
ResourceFunction["ToDirectedAcyclicGraph"][PetersenGraph[6, 2], #,
VertexStyle -> {# -> Orange}, VertexSize -> {# -> 1/4}] & /@ {1,
7},
PetersenGraph[6, 2]]}, Frame -> All, FrameStyle -> Lighter[Gray],
Spacings -> {2, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/4ffd1416ce6a27a7.png)
![Grid[Partition[Show[#, ImageSize -> 100] & /@ ReplacePart[Map[
ResourceFunction["ToDirectedAcyclicGraph"][
PetersenGraph[6, 2], {1, #},
VertexStyle -> {1 -> Magenta, # -> Orange},
VertexSize -> {1 -> 1/4, # -> 1/4},
"ConflictedEdges" -> True,
EdgeStyle -> {UndirectedEdge[_, _] -> LightGray,
DirectedEdge[_, _] -> Gray}] &, Range[12]],
{1 -> Graph[{}]}], 6]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/7b7ada6145369cc7.png)
![Grid[Prepend[{CycleGraph[#],
ResourceFunction["ToDirectedAcyclicGraph"][CycleGraph[#], 1,
VertexStyle -> {1 -> Orange}, VertexSize -> {1 -> 1/16}]
} & /@ {3, 4, 5},
Text /@ {"Input", "Output"}], Frame -> All,
FrameStyle -> Lighter[Gray], Spacings -> {2, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/0fc6a6e02ce0a25a.png)
![With[{graph0 = Last[SortBy[
ConnectedGraphComponents[
SeedRandom["GraphTest"];
RandomGraph[{30, 30}]],
VertexCount]]}, Grid[Partition[
Show[#, ImageSize -> 250] & /@ Prepend[
ResourceFunction["ToDirectedAcyclicGraph"][graph0, #,
VertexStyle -> {# -> Orange},
VertexSize -> {# -> 1/2},
"ConflictedEdges" -> True,
EdgeStyle -> {UndirectedEdge[_, _] -> Lighter@Gray,
DirectedEdge[_, _] -> Arrowheads[1/25]}
] &@# & /@ RandomSample[
VertexList[graph0]][[{1, 3, 5}]],
graph0], 2], Frame -> All,
FrameStyle -> Lighter[Gray],
Spacings -> {2, 2}]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/118085467673f551.png)
![Grid[{Text /@ {"Input", "Output", "Output"},
Prepend[
ResourceFunction["ToDirectedAcyclicGraph"][PetersenGraph[8, 2], #,
VertexStyle -> {# -> Orange}, VertexSize -> {# -> 1/4},
VertexCoordinates -> Automatic
] & /@ {1, 9}, PetersenGraph[8, 2]]},
Frame -> All, FrameStyle -> Lighter[Gray],
Spacings -> {2, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/5c687f944283051e.png)
![With[{graph0 = Last[SortBy[
ConnectedGraphComponents[
SeedRandom["GraphTest"];
RandomGraph[{30, 30}]],
VertexCount]]}, Grid[Partition[
(*Show[#,ImageSize->250]&/@*)Prepend[
ResourceFunction["ToDirectedAcyclicGraph"][graph0, #,
VertexStyle -> {# -> Orange},
VertexSize -> {# -> 1/4},
VertexCoordinates -> Automatic,
GraphLayout -> "LayeredDigraphEmbedding",
"ConflictedEdges" -> True,
EdgeStyle -> {UndirectedEdge[_, _] -> LightGray,
DirectedEdge[_, _] -> Arrowheads[1/25]}
] &@# & /@ RandomSample[
VertexList[graph0]][[{1, 4, 5}]],
graph0], 2], Frame -> All,
FrameStyle -> Lighter[Gray],
Spacings -> {2, 2}]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/50c852a21c17f71c.png)
![SeedRandom["GraphTest"];
gResolved = ResourceFunction["ToDirectedAcyclicGraph"][RandomGraph[{30, 30}], 1,
"CollisionFunction" -> (# &),
GraphLayout -> "LayeredDigraphEmbedding",
VertexCoordinates -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/2dcf465afc7c2d2d.png)
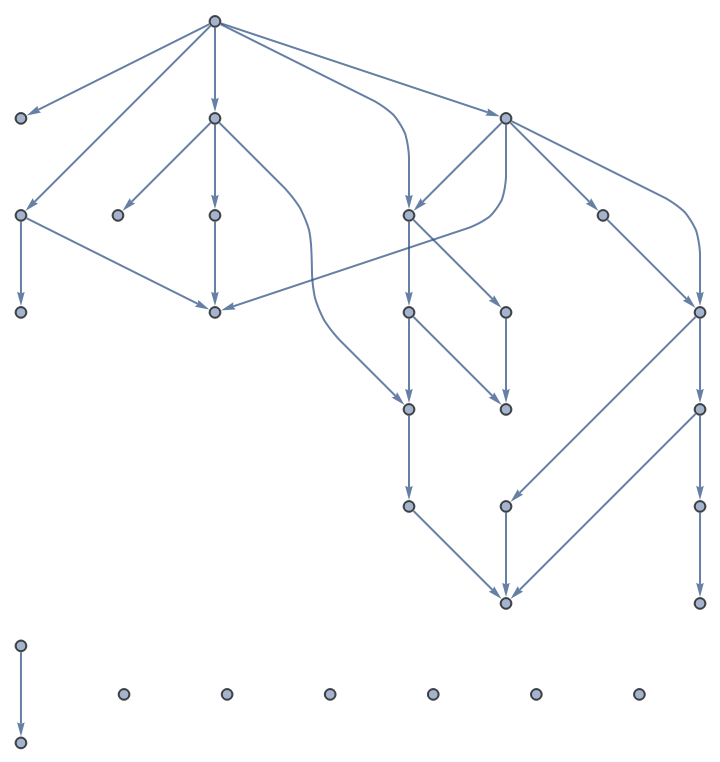
![Length[Union[(Length /@ FindPath[
gResolved, 1, #, Infinity, All])]
] & /@ VertexList[gResolved]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/2ad7e636815a87c5.png)
![With[{graph0 = Last[SortBy[
ConnectedGraphComponents[RandomGraph[{30, 30}]],
VertexCount]]}, SameQ[Outer[GraphDistance[
ResourceFunction["ToDirectedAcyclicGraph"][graph0, #1], #1, #2] &,
VertexList[graph0], VertexList[graph0], 1],
GraphDistanceMatrix[graph0]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/670b6b14d97c9055.png)
![SeedRandom["GraphTest"];
With[{graph0 = RandomGraph[{100, 200}]},
IsomorphicGraphQ[
ResourceFunction["ToDirectedAcyclicGraph"][graph0, 1,
"CollisionFunction" -> Identity],
DirectedGraph[Graph[SortBy[VertexList[graph0],
GraphDistance[graph0, 1, #] &], EdgeList[graph0]
], "Acyclic"]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/4bf100b06f345327.png)
![ResourceFunction["ToDirectedAcyclicGraph"][CycleGraph[6], {1, 4},
"ConflictedEdges" -> True,
VertexStyle -> {1 -> Red, 4 -> Blue, 2 | 3 | 5 | 6 -> Green},
VertexSize -> {1 -> 1/10, 4 -> 1/10},
EdgeStyle -> {UndirectedEdge[_, _] -> LightGray,
DirectedEdge[_, _] -> Darker@Gray}]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/62597cf94134d17c.png)
![With[{g1 = GraphUnion[CycleGraph[4],
VertexReplace[CycleGraph[3], x_ :> x + 4]]},
Row[{g1, Style["\[LongRightArrow]", 32, Gray, Bold],
ResourceFunction["ToDirectedAcyclicGraph"][g1, 1,
VertexStyle -> {1 -> Orange},
VertexSize -> {1 -> 1/4},
ImageSize -> 200]},
Spacer[10]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/788b4193d4037361.png)
![With[{g1 = GraphUnion[CycleGraph[4],
VertexReplace[CycleGraph[3], x_ :> x + 4]]},
Row[{g1, Style["\[LongRightArrow]", 32, Gray, Bold],
ResourceFunction["ToDirectedAcyclicGraph"][g1, {1, 5},
VertexStyle -> {1 -> Orange, 5 -> Magenta},
VertexSize -> {1 -> 1/4, 5 -> 1/4},
ImageSize -> 200]},
Spacer[10]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/3f1c607b255ad88d.png)
![CountWalks[graph0_, loc_] := CountWalks[graph0, loc
] = If[MemberQ[{1, {1, 1}}, loc], 1, Total[Cases[EdgeList[graph0],
DirectedEdge[pre_, loc
] :> CountWalks[graph0, pre]]]];](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/210975440db91162.png)
![TableForm[countWalksTable = Table[With[
{graph0 = ResourceFunction["ToDirectedAcyclicGraph"][PetersenGraph[i, j], 1]},
Total[CountWalks[graph0, #] & /@ Select[VertexList[graph0],
SameQ[Cases[EdgeList[graph0], DirectedEdge[#, _]], {}] &]]],
{i, 3, 20}, {j, 1, i}]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/4c9ff536302f655e.png)
![Grid[Riffle[Partition[
ResourceFunction["ToDirectedAcyclicGraph"][PetersenGraph[#, 2], 1,
VertexStyle -> {1 -> Orange}, VertexSize -> {1 -> 1/4},
"ConflictedEdges" -> True,
EdgeStyle -> {UndirectedEdge[_, _] -> LightGray}]
& /@ Range[5, 10], 3], Partition[countWalksTable[[3 ;; 9, 2]], 3]]]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/4a9a97eb1c0bd2a7.png)
![unusualGridGraph = ResourceFunction["ToDirectedAcyclicGraph"][With[
{g1 = NearestNeighborGraph[Position[Array[1 &, {5, 5}], 1]]},
EdgeAdd[g1, Flatten@Outer[If[SameQ[#2 - #1, {1, 1}],
UndirectedEdge[#1, #2], {}] &, #, #, 1]] &@
VertexList[g1]], {1, 1}, "CollisionFunction" -> (-# &)]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/2cbe874bec94ecb5.png)
![CountWalks[graph0_, loc_] := CountWalks[graph0, loc
] = If[MemberQ[{1, {1, 1}}, loc], 1, Total[Cases[EdgeList[graph0],
DirectedEdge[pre_, loc
] :> CountWalks[graph0, pre]]]];](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/0de54d7e026f0d29.png)
![Graph[unusualGridGraph, VertexLabels -> (
# -> Placed[CountWalks[unusualGridGraph, #],
Center] & /@ VertexList[unusualGridGraph]),
VertexSize -> 1/3, VertexStyle -> Directive[White, EdgeForm[LightGray]],
EdgeStyle -> Gray]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5d21cab-4741-4682-910c-eda8dda303ae/486e21c071a24e65.png)