Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the tangent vector of a curve
ResourceFunction["TangentVector"][c,t] computes the tangent vector of a curve c parametrized by t. |
Calculate the value of the tangent vector of a curve:
| In[1]:= |
| Out[1]= |
Plot a set of tangent vectors:
| In[2]:= | ![ParametricPlot[{Cos[t], Sin[t] Cos[t]}, {t, 0, 2 \[Pi]}, Epilog -> Table[Arrow[{{Cos[tf], Sin[tf] Cos[
tf]}, ({Cos[t], Sin[t] Cos[t]} + .3 ResourceFunction[
"TangentVector"][{Cos[t], Sin[t] Cos[t]}, t] /. t -> tf)}], {tf, 0, 2 \[Pi], 2 \[Pi]/50}]]](https://www.wolframcloud.com/obj/resourcesystem/images/4ca/4ca5da05-ce92-4737-b888-2896eb2741af/6358438a87d4b716.png) |
| Out[2]= | 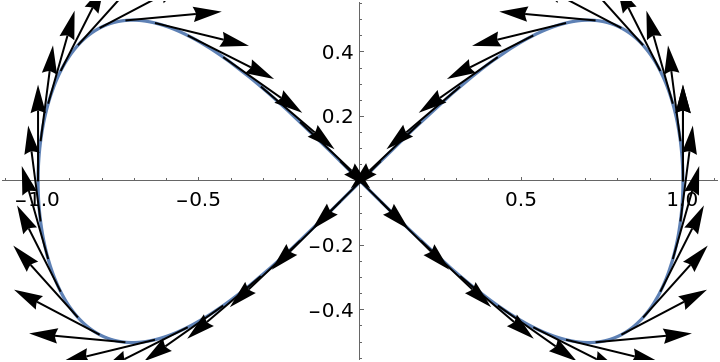 |
The tangent vector of a figure-eight curve:
| In[3]:= | ![Manipulate[
ParametricPlot[{Cos[t], Sin[t] Cos[t]}, {t, 0, 2 \[Pi]}, Epilog -> Arrow[{{Cos[tf], Sin[tf] Cos[
tf]}, ({Cos[t], Sin[t] Cos[t]} + .3 ResourceFunction[
"TangentVector"][{Cos[t], Sin[t] Cos[t]}, t] /. t -> tf)}]], {tf, .1, 2 \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/4ca/4ca5da05-ce92-4737-b888-2896eb2741af/7d518beb23e214dd.png) |
| Out[3]= | 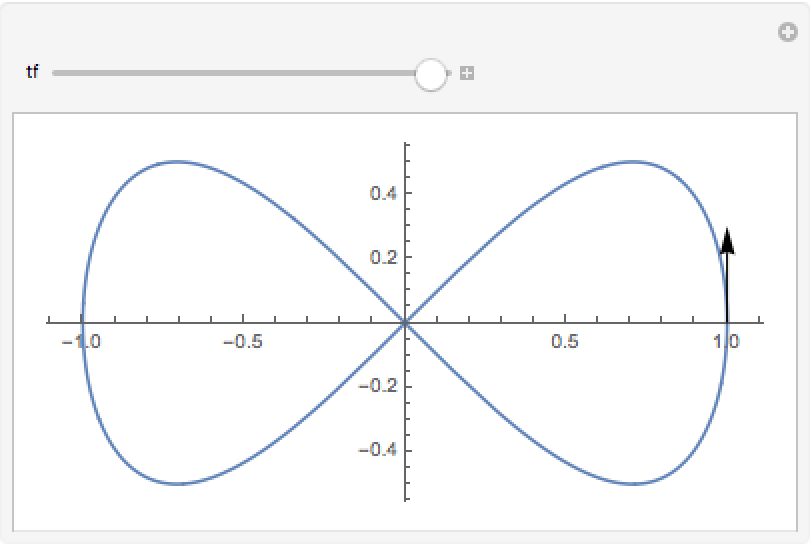 |
Define a helix:
| In[4]:= |
| Out[4]= |
The tangent developable surface of a curve is generated by the tangent vector field of the curve. It can be calculated using the resource function TangentDevelopableSurface:
| In[5]:= |
| Out[5]= |
This is alternatively formed by adding a multiple of the tangent vector to the curve:
| In[6]:= |
| Out[6]= |
Plot the surface:
| In[7]:= |
| Out[7]= | 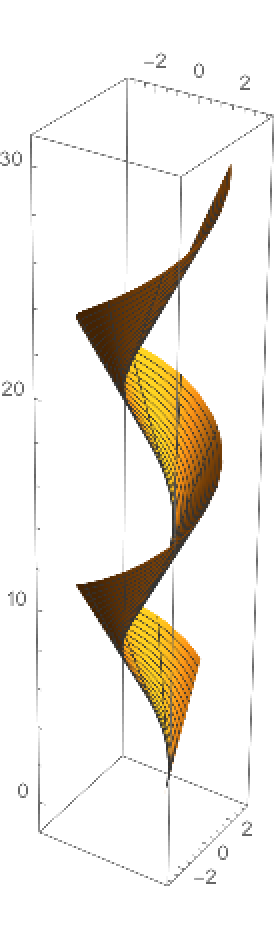 |
A unit speed helix:
| In[8]:= | ![uhelix = {a Cos[t/Sqrt[a^2 + b^2]], a Sin[t/Sqrt[a^2 + b^2]], (b t)/
Sqrt[a^2 + b^2]};](https://www.wolframcloud.com/obj/resourcesystem/images/4ca/4ca5da05-ce92-4737-b888-2896eb2741af/0052c47164ced766.png) |
The curvature, via the resource function Curvature:
| In[9]:= |
| Out[9]= |
The tangent vector:
| In[10]:= |
| Out[10]= | 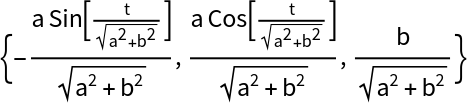 |
The derivative of the tangent vector:
| In[11]:= |
| Out[11]= |
The normal vector, via the resource function NormalVector:
| In[12]:= |
| Out[12]= |
The curvature times the normal vector is equal to the derivative of the tangent vector:
| In[13]:= |
| Out[13]= |
In relation with the Frenet-Serret system, the tangent vector is the first entry of the second List:
| In[14]:= |
| Out[14]= | 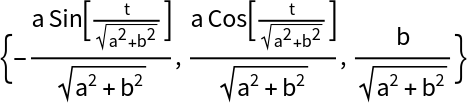 |
This work is licensed under a Creative Commons Attribution 4.0 International License