Function Repository Resource:

NormalVector

Source Notebook

Compute the normal vector of a curve

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["NormalVector"][c,t]

computes the normal vector for a curve c parametrized by t.

Details and Options

The normal vector, or simply the "normal" to a curve, is a vector perpendicular to a curve or surface at a given point. It is usually represented by

.

Examples

Basic Examples (2)

A unit speed helix:

In[1]:=

$uhelix = {a Cos[t/Sqrt[a^2 + b^2]], a Sin[t/Sqrt[a^2 + b^2]], (b t)/ Sqrt[a^2 + b^2]};$

Compute the normal vector:

In[2]:=

Out[2]=

Scope (3)

The normal vector of a figure-eight curve:

In[3]:=

Out[3]=

In[4]:=

$Manipulate[ ParametricPlot[{Cos[t], Sin[t] Cos[t]}, {t, 0, 2 \[Pi]}, Epilog -> Arrow[{{Cos[tf], Sin[tf] Cos[ tf]}, ({Cos[t], Sin[t] Cos[t]} + .3 ResourceFunction[ "NormalVector"][{Cos[t], Sin[t] Cos[t]}, t] /. t -> tf)}], PlotRange -> {{-1.3, 1.3}, {-.8, .8}}], {tf, .1, 2 \[Pi]}]$

Out[4]=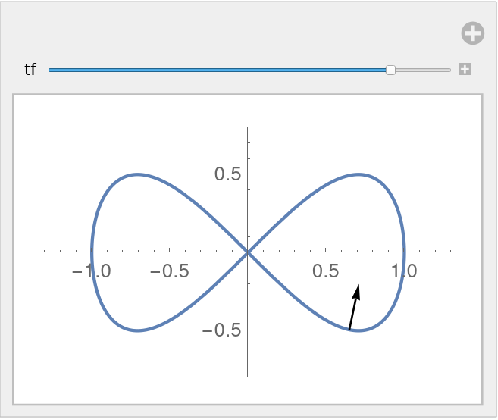

Plot a set of normal vectors:

In[5]:=

$ParametricPlot[{Cos[t], Sin[t] Cos[t]}, {t, 0, 2 \[Pi]}, Epilog -> Table[Line[{{Cos[tf], Sin[tf] Cos[ tf]}, ({Cos[t], Sin[t] Cos[t]} + .5 ResourceFunction[ "NormalVector"][{Cos[t], Sin[t] Cos[t]}, t] /. t -> tf)}], {tf, 0, 2 \[Pi], .1}], PlotRange -> {{-1.5, 1.3}, {-1, 1}}]$

Out[5]=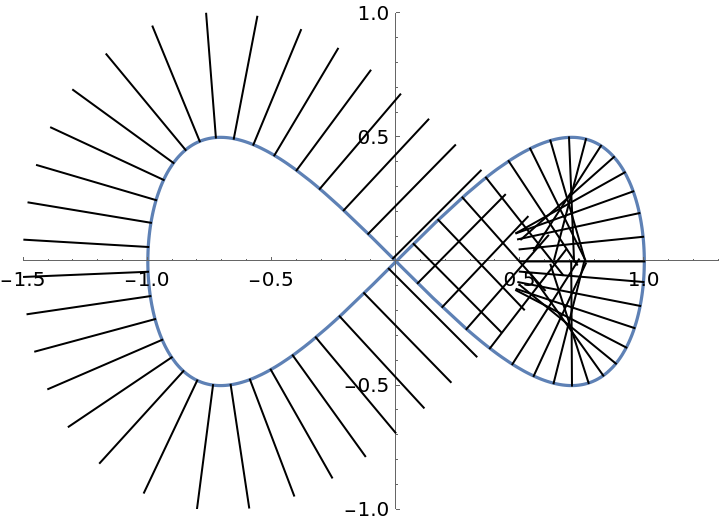

Define a helix curve:

In[6]:=

Compute the normal vector:

In[7]:=

Out[7]=

The binormal vector, via the resource function BinormalVector:

In[8]:=

Out[8]=

The normal plane is spanned by the normal vector and the binormal vector. It can be computed with the resource function NormalPlane:

In[9]:=

Out[9]=

The normal plane and the normal vector along the helix:

In[10]:=

Manipulate[
Show[ParametricPlot3D[helix, {t, 0, 3}], Graphics3D[{Arrow[{helix, helix + {-Cos[t], -Sin[t], 0}}], Opacity[.5], ResourceFunction[
ResourceObject[<|{"Name" -> "NormalPlane", "ShortName" -> "NormalPlane", "UUID" -> "e083b2e5-d843-4dc2-98e5-9a20518341ee", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Compute the normal plane of a space curve", "RepositoryLocation" -> URL[
"https://www.wolframcloud.com/objects/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$495e9b14e5184131aa3c629c6d3c8005`NormalPlane", "FunctionLocation" -> CloudObject[
"https://www.wolframcloud.com/obj/a318e75b-f17d-4c12-bda1-8414ee7e1565"]}|>, {ResourceSystemBase -> Automatic}]][helix, t]} /. t -> tf], PlotRange -> {{-1, 1}, {-1, 1}, {-1, 3}}], {{tf, 1}, 0, 3}]

Out[10]=

Properties and Relations (2)

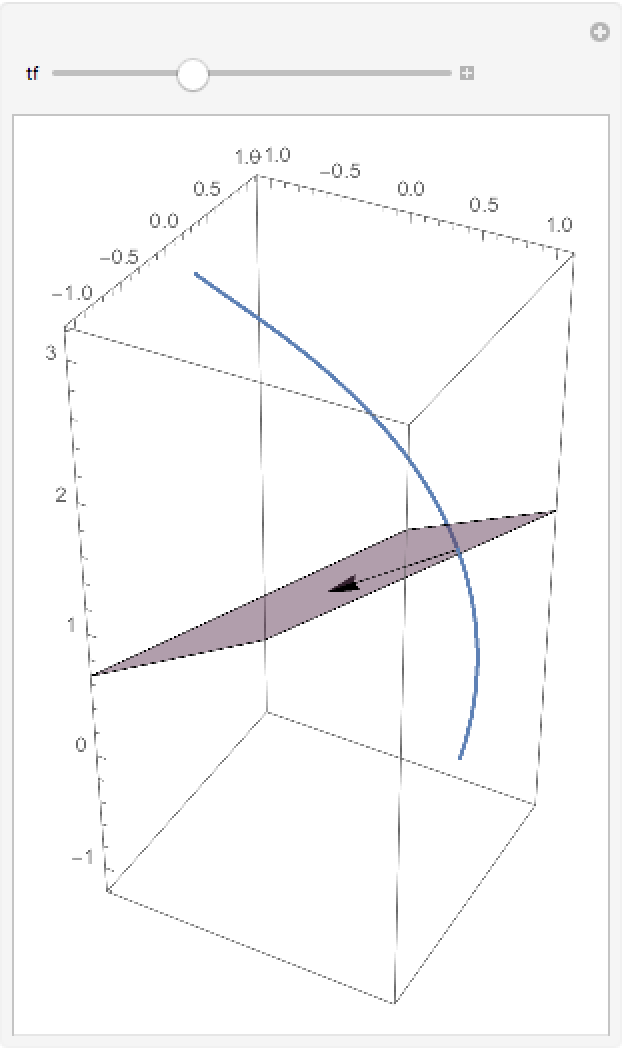The definition of Viviani's curve:

In[11]:=

Out[11]=

Plot the curve:

In[12]:=

$vp = ParametricPlot3D[Evaluate[viviani], {t, -2 \[Pi], 2 \[Pi]}, PlotStyle -> Thickness[.02]]$

Out[12]=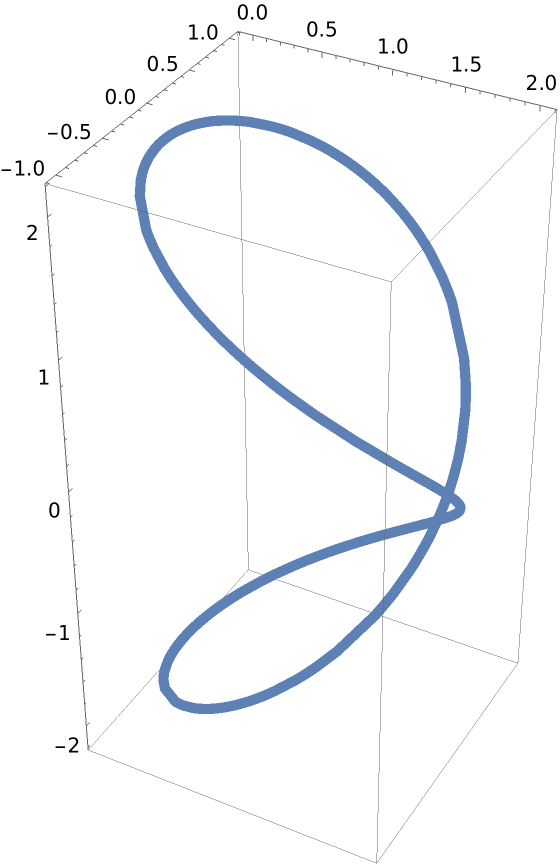

The normal surface associated to a curve is generated by its normal vector field. It can be computed with the resource function NormalSurface:

In[13]:=

Out[13]=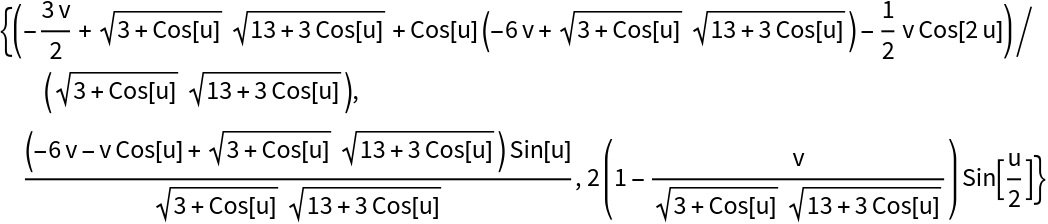

Plot the normal surface:

In[14]:=

$nsp = ParametricPlot3D[ Evaluate[ns], {u, -2 \[Pi], 2 \[Pi]}, {v, -1, -.05}, PlotPoints -> {80, 10}]$

Out[14]=

A unit speed helix:

In[15]:=

$uhelix = {a Cos[t/Sqrt[a^2 + b^2]], a Sin[t/Sqrt[a^2 + b^2]], (b t)/ Sqrt[a^2 + b^2]};$

Compute the normal vector:

In[16]:=

Out[16]=

Compute the curvature with the resource function Curvature:

In[17]:=

$\[Kappa] = Simplify[ResourceFunction["Curvature"][uhelix, t], a > 0 && b > 0 && t > 0]$

Out[17]=

Compute the torsion with the resource function CurveTorsion:

In[18]:=

$\[Tau] = Simplify[ResourceFunction["CurveTorsion"][uhelix, t], a > 0 && b > 0 && t > 0]$

Out[18]=

Compute the tangent vector with the resource function TangentVector:

In[19]:=

Out[19]=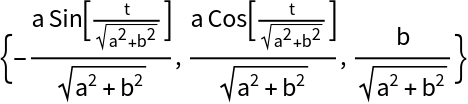

Compute the binormal vector with the resource function BinormalVector:

In[20]:=

Out[20]=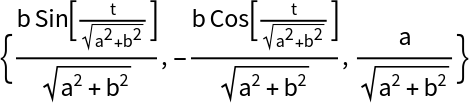

Compute the following quantity:

In[21]:=

$FullSimplify[-\[Kappa] tan + \[Tau] binormal, t > 0 && a > 0]$

Out[21]=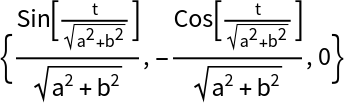

The previous expression is the derivative of the normal:

In[22]:=

Out[22]=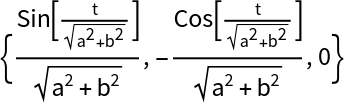

Using FrenetSerretSystem, the normal vector is the second entry of the second List:

In[23]:=

Out[23]=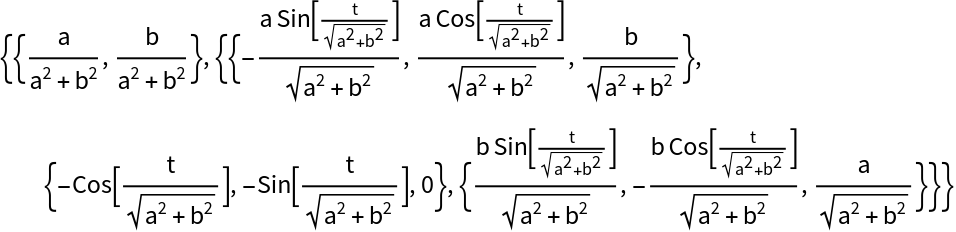

Publisher

Version History

2.0.0 – 30 April 2020
1.0.0 – 28 April 2020

Source Metadata

Citation:
- Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License