Basic Examples (2)
Find the position of 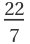 in the Stern–Brocot sequence:
in the Stern–Brocot sequence:
Find the position of 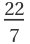 in the Stern–Brocot sequence with explicit numerator and denominator:
in the Stern–Brocot sequence with explicit numerator and denominator:
Find the fraction at position 960 in the Stern–Brocot sequence:
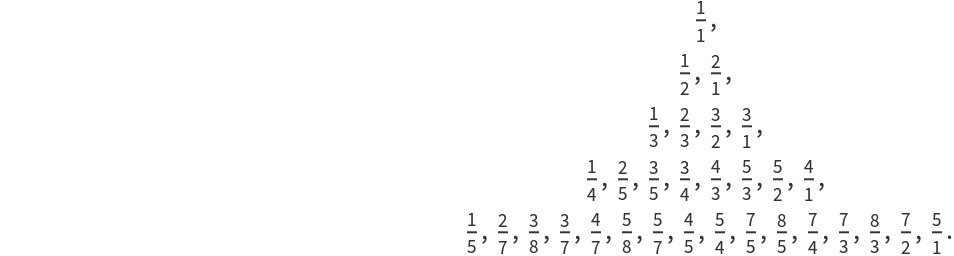
Generate terms of the Farey sequence:
Show their positions in the Stern–Brocot sequence:
Use the positions to generate fractions:
Scope (4)
Show the first 42 terms:
Get back the positions using explicit numerators and denominators:
Get back the positions by forcing a denominator of 1 everywhere:
A two term form is needed for positions of integers since fractions  ,
, ,
, ,
, are returned as 1, 2, 3, 4:
are returned as 1, 2, 3, 4:
Properties and Relations (6)
Negative values return negative fractions:
Negative fractions correspond to negative positions:
Level 5 of the Stern-Brocot tree:
Find the Total of the terms of the ContinuedFraction for level 5 of the Stern-Brocot tree:
For terms 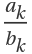 on the same level in the Stern–Brocot binary tree,
on the same level in the Stern–Brocot binary tree, 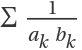 =1:
=1:
The maximal numerator for level n of the Stern-Brocot tree is Fibonacci[n+1]:
An unreduced fraction gives the same value as the reduced fraction:
Create a plot of the first 256 values:
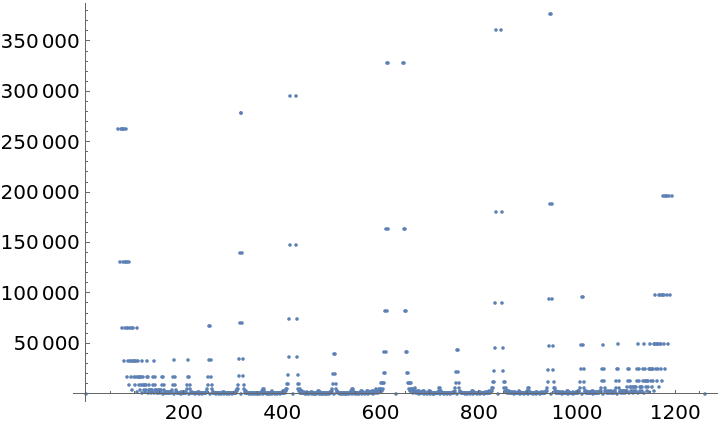
Create a plot of indices for the Farey sequence fractions:
Possible Issues (3)
Fractions at positions 2a-1 are returned as a instead of 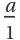 :
:
SternBrocot returns a Failure if its input is anything other than an integer:
Fractions leading to an index with more than a million digits will be flagged as out of range:
Fractions with a million digit index will be evaluated as expected:
Neat Examples (4)
Find fractions of the order 8 FareySequence missing from the order 5 Stern–Brocot binary tree:
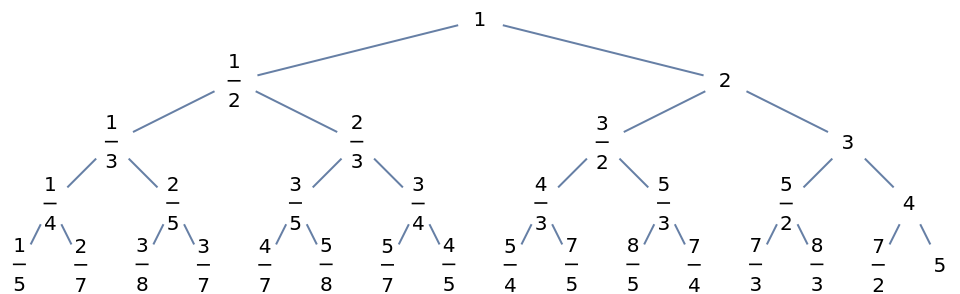
Show the Stern–Brocot binary tree:
Put the Stern–Brocot binary tree into a hydraulic press:
Make the Stern–Brocot binary tree with help from IntegerExponent:
![]() in the Stern–Brocot sequence:
in the Stern–Brocot sequence:![]() in the Stern–Brocot sequence with explicit numerator and denominator:
in the Stern–Brocot sequence with explicit numerator and denominator: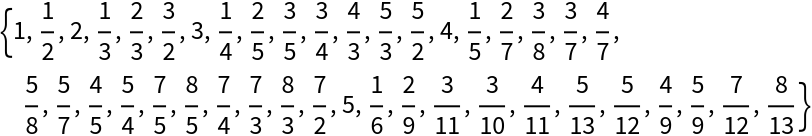
![]() ,
,![]() ,
,![]() ,
,![]() are returned as 1, 2, 3, 4:
are returned as 1, 2, 3, 4:
![]() on the same level in the Stern–Brocot binary tree,
on the same level in the Stern–Brocot binary tree, ![]() =1:
=1: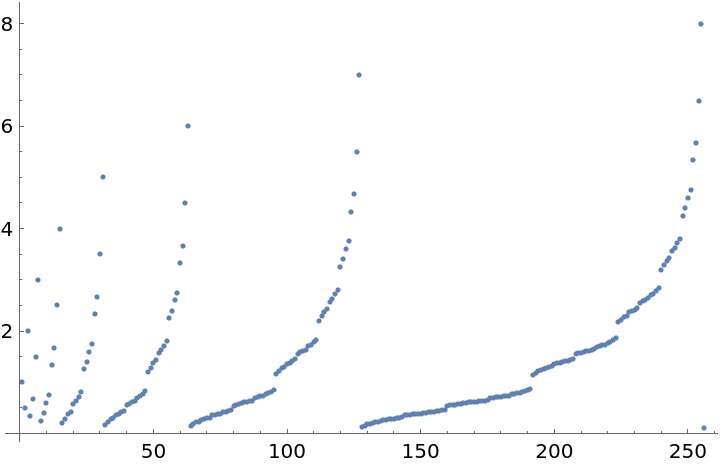
![]() :
:
![Graph[EdgeList[CompleteKaryTree[5, 2]] /. Thread[Range[31] -> ResourceFunction["SternBrocot"][Range[31]]], VertexLabels -> Placed[Automatic, Center], VertexSize -> .75, VertexShapeFunction -> Nothing, ImageSize -> 480]](https://www.wolframcloud.com/obj/resourcesystem/images/380/380d1109-a07e-4c15-80a2-d8b4a97a21c8/1c2252db26933468.png)
![part = Complement[FareySequence[8], missed];
flatten = Join[part, Drop[Reverse[1/part], 1]];
Style[Row[flatten, " "], 12]](https://www.wolframcloud.com/obj/resourcesystem/images/380/380d1109-a07e-4c15-80a2-d8b4a97a21c8/7cf102857e69d50e.png)
![Graphics[
MapIndexed[
Style[Text[#1, {#2[[1]], 6 IntegerExponent[#2[[1]], 2]}], 9] &, Sort[ResourceFunction["SternBrocot"][Range[2^6 - 1]]]], ImageSize -> Medium]](https://www.wolframcloud.com/obj/resourcesystem/images/380/380d1109-a07e-4c15-80a2-d8b4a97a21c8/71e14909c649d006.png)
