Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a complete binary tree of positive fractions
ResourceFunction["CalkinWilfTree"][n] generates a complete binary tree of the positive fractions in the Calkin-Wilf sequence down to level n. |
Generate a complete binary tree of the positive fractions in the Calkin-Wilf sequence down to level 4:
| In[1]:= |
| Out[1]= | 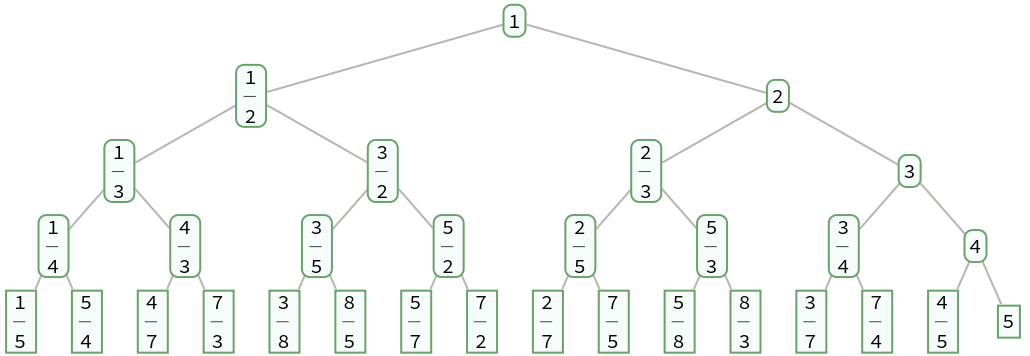 |
A fraction ![]() has children
has children ![]() and
and ![]() :
:
| In[2]:= |
| Out[2]= | 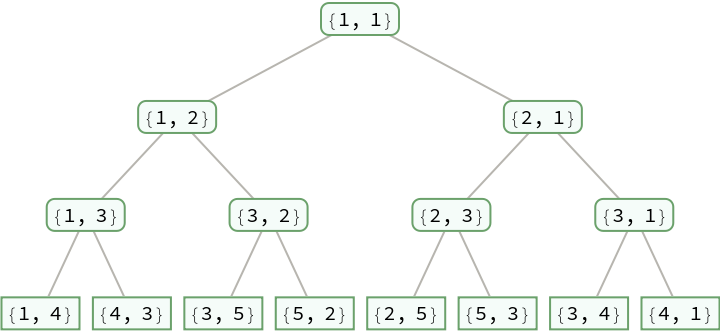 |
| In[3]:= |
| Out[3]= |
The fractions on level d are those for which the total of the terms in its continued fraction representation is d+1:
| In[4]:= |
| Out[4]= | 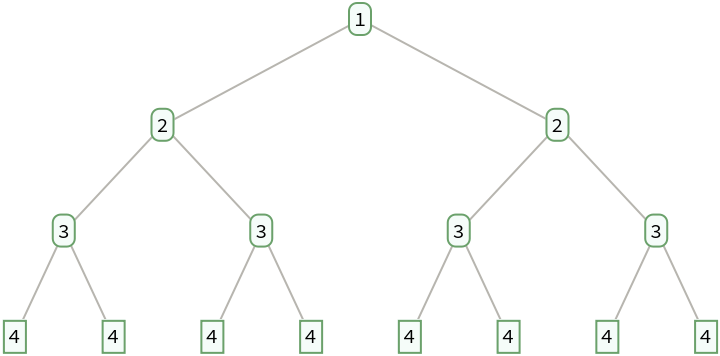 |
The numerators of the fractions in a breadth-first traversal give Stern's diatomic series:
| In[5]:= |
| Out[5]= | 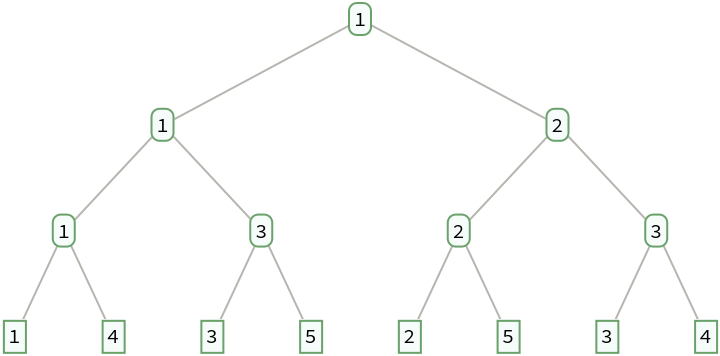 |
| In[6]:= |
| Out[6]= |
The terms of Stern's diatomic series are generated by the fusc function:
| In[7]:= |
| Out[7]= |
Additionally, the denominators give Stern's diatomic series shifted by one:
| In[8]:= |
| Out[8]= | 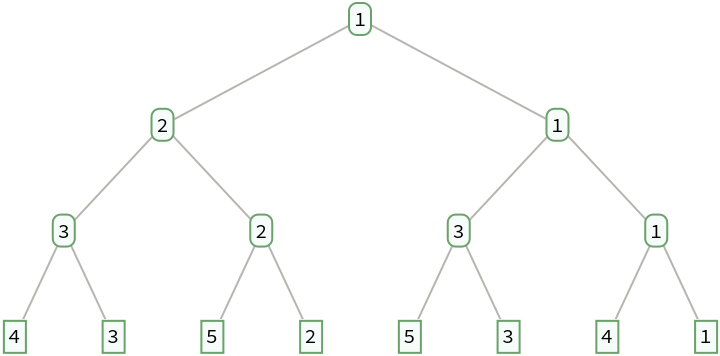 |
| In[9]:= |
| Out[9]= |
If ![]() ,
, ![]() , …,
, …, ![]() are the fractions at level d, then
are the fractions at level d, then 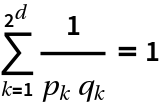 :
:
| In[10]:= |
| Out[10]= | 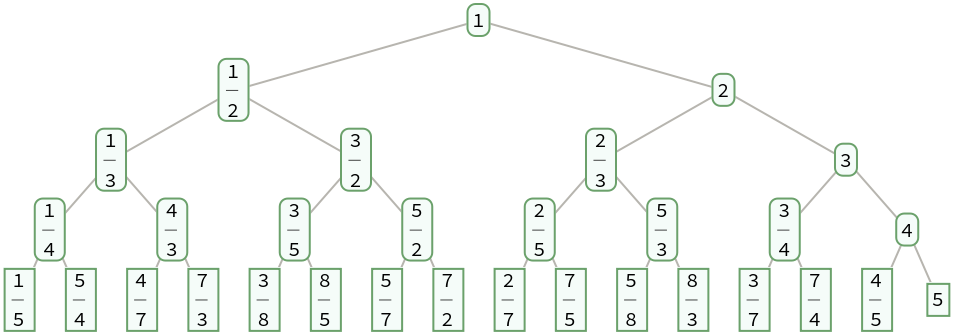 |
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= |
Define a function that permutes the positions on level d by reversing the corresponding binary integers with d digits:
| In[13]:= |
Permute the fractions on each level of a Calkin-Wilf tree:
| In[14]:= |
| In[15]:= |
| Out[15]= | 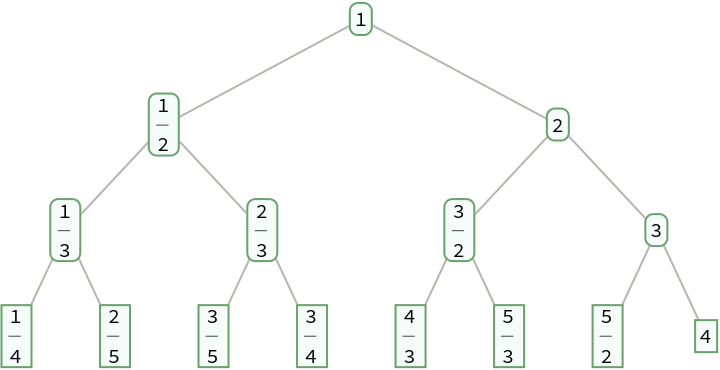 |
The result is a Stern-Brocot tree:
| In[16]:= |
| Out[17]= |
This work is licensed under a Creative Commons Attribution 4.0 International License