Function Repository Resource:

SternBrocotTree

Source Notebook

Generate a complete binary search tree of positive fractions

Contributed by: Ian Ford (Wolfram Research)

ResourceFunction["SternBrocotTree"][n]

generates a complete binary search tree of the positive fractions down to level n.

Details and Options

The fractions on level d are those for which the total of the terms in its continued fraction representation is d+1.

In ResourceFunction["SternBrocotTree"][n], n can be any non-negative machine integer.

ResourceFunction["SternBrocotTree"] takes the same options as Tree.

Examples

Basic Examples (1)

Generate a complete binary search tree of the positive fractions down to level 4:

In[1]:=

Out[1]=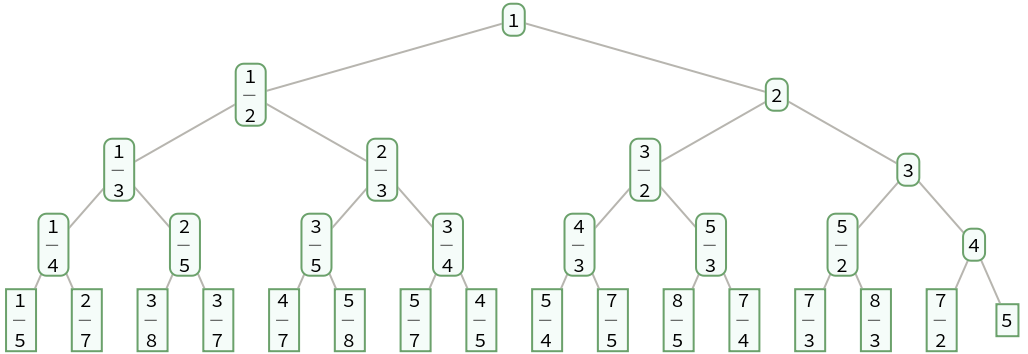

Applications (1)

Approximate Pi as a rational number with a continued fraction representation with terms totalling 10:

In[2]:=

In[3]:=

$search[tree_, x_] := Module[{data = TreeData[tree], left, right}, If[TreeLeafQ[tree], data, {left, right} = TreeChildren[tree]; Switch[NumericalOrder[data, x], 1, search[right, x], -1, search[left, x], 0, data]]]$

In[4]:=

Out[4]=

In[5]:=

Out[5]=

Properties and Relations (7)

FareySequence[n] gives the list of fractions in SternBrocotTree[n-1] between 0 and 1 with denominators not exceeding n:

In[6]:=

Out[6]=

In[7]:=

Out[7]=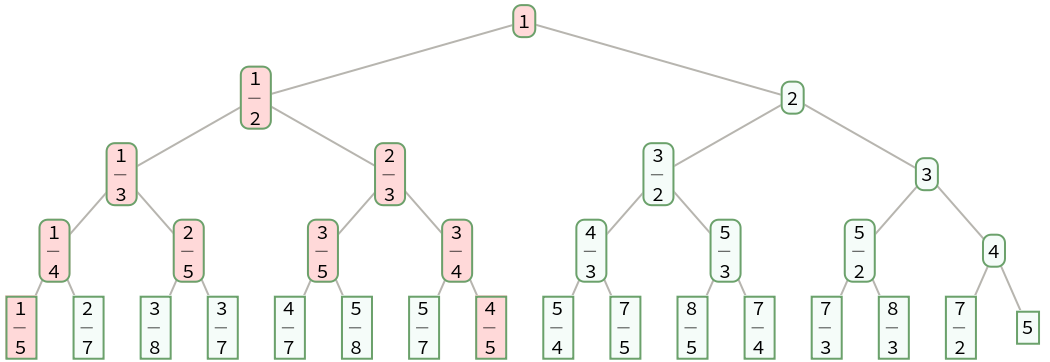

SternBrocotTree gives a sorted binary tree, also known as a search tree:

In[8]:=

$inorder[q_, {q1_, q2_}] /; q1 < q < q2 := q inorder[_, _] := "not sorted"$

In[9]:=

Out[9]=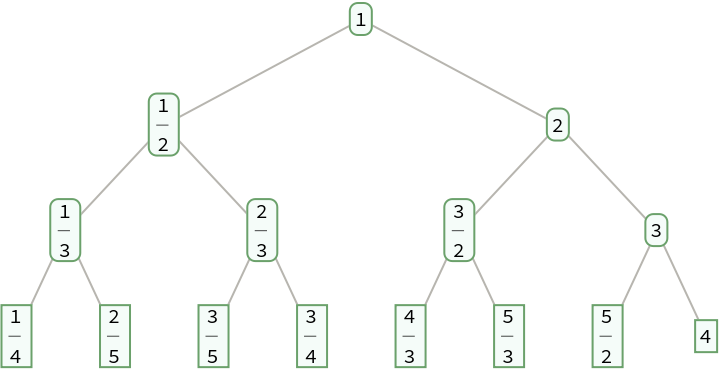

In[10]:=

Out[10]=

A fraction with a continued fraction representation {a₁,…,a_k} has children with continued fraction representations {a₁,…,a_k-1,2} and {a₁,…,a_k+1}:

In[11]:=

$NestTree[ Replace[{as___, a_} :> SortBy[{{as, a - 1, 2}, {as, a + 1}}, FromContinuedFraction]], {1}, 3]$

Out[11]=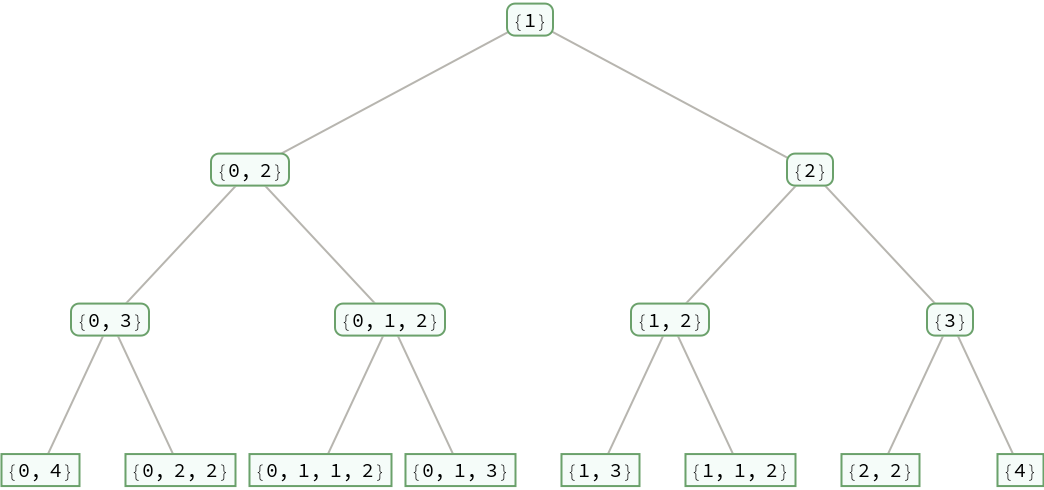

In[12]:=

Out[12]=

The fractions on level d are those for which the total of the terms in its continued fraction representation is d+1:

In[13]:=

Out[13]=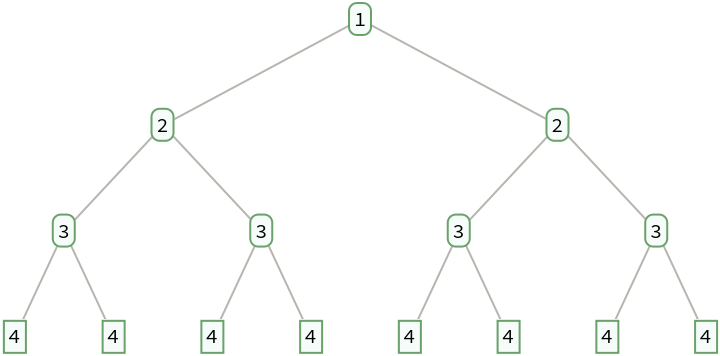

The fractions given by SternBrocotTree can be obtained by successively taking the sums of the numerators and denominators of consecutive pairs of fractions starting with 0 and Infinity:

In[14]:=

Out[14]=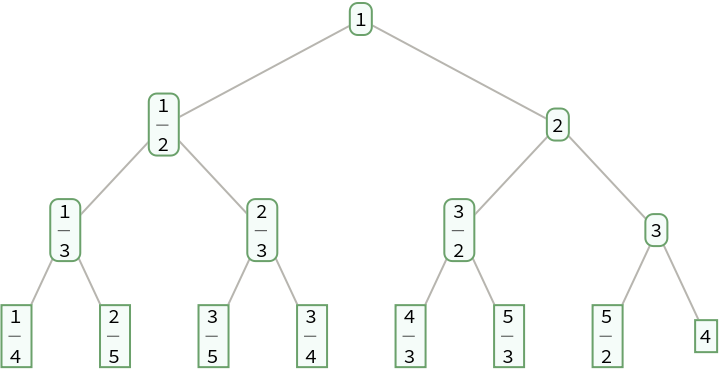

In[15]:=

$mediant[{q1_, Infinity}] := Apply[Divide, NumeratorDenominator[q1] + {1, 0}] mediant[{q1_, q2_}] := Divide @@ Total[NumeratorDenominator[{q1, q2}]]$

In[16]:=

$split[{q1_, q2_}] := Splice[{mediant[{q1, q2}], q2}]$

In[17]:=

Out[17]=

In[18]:=

Out[18]=

In[19]:=

Out[19]=

In[20]:=

Out[20]=

In[21]:=

Out[21]=

The convergents of a positive fraction are a subset of its ancestors in the Stern-Brocot tree:

In[22]:=

Out[22]=

In[23]:=

Out[23]=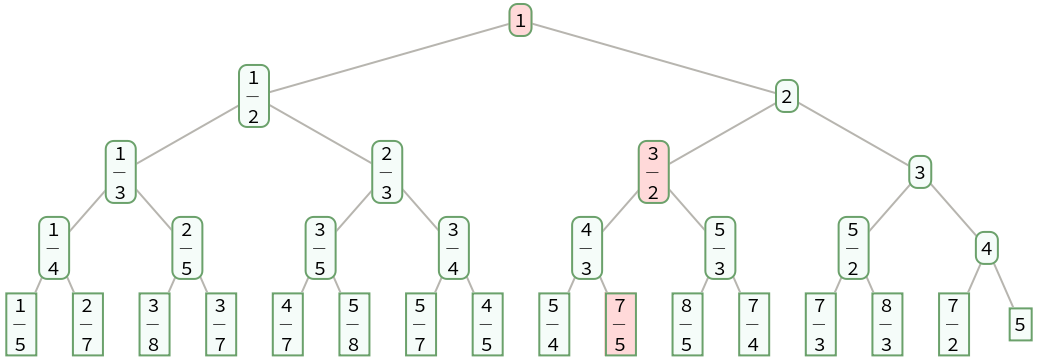

In[24]:=

Out[24]=

If , , …, are the fractions at level d, then :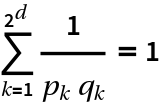

In[25]:=

Out[25]=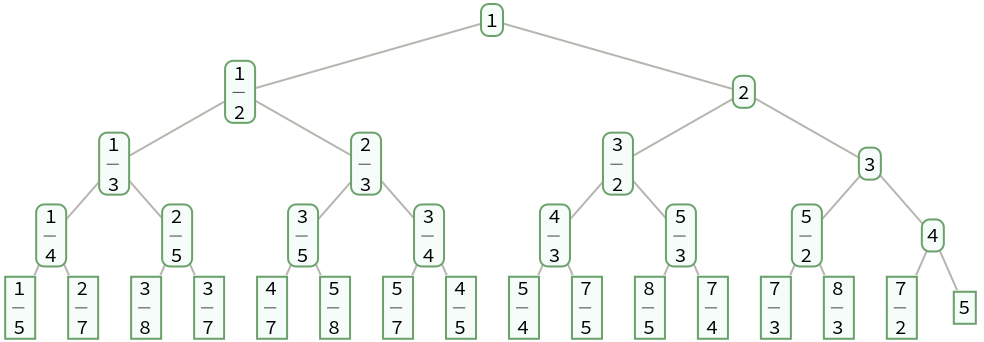

In[26]:=

Out[26]=

In[27]:=

Out[27]=

Define a function that permutes the positions on level d by reversing the corresponding binary integers with d digits:

In[28]:=

Permute the fractions on each level of a Stern-Brocot tree:

In[29]:=

In[30]:=

Out[30]=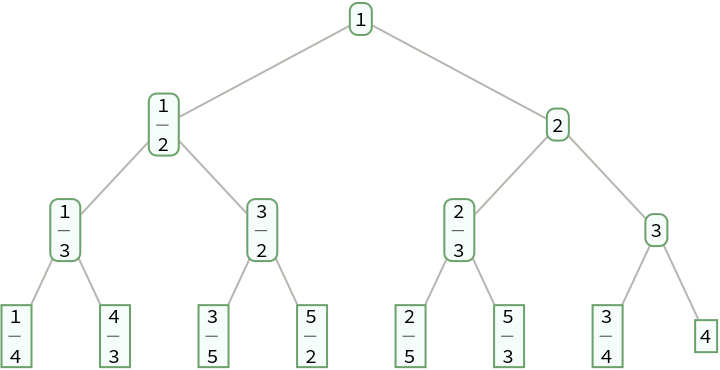

The result is a Calkin-Wilf tree:

In[31]:=

Out[32]=

Version History

1.0.0 – 06 January 2023

Source Metadata

Citation:
- Weisstein, Eric W. "Stern-Brocot Tree." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/Stern-BrocotTree.html.
- Gibbons, J., Lester, D., Bird, R. "FUNCTIONAL PEARLS: Enumerating the rationals." Journal of Functional Programming, 16(3), 281-291. https://doi.org/10.1017/S0956796806005880
- Bates, B., Bunder, M., Tognetti, K. "Linking the Calkin-Wilf and Stern-Brocot trees." European Journal of Combinatorics, Volume 31, Issue 7, 2010, Pages 1637-1661, ISSN 0195-6698. https://doi.org/10.1016/j.ejc.2010.04.002.
- Pawlewicz, J. "Order Statistics in the Farey Sequences in Sublinear Time." In: Arge, L., Hoffmann, M., Welzl, E. (eds) Algorithms – ESA 2007. ESA 2007. Lecture Notes in Computer Science, vol 4698. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-75520-3_ 21.

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

SternBrocotTree

Details and Options