Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RoseCurveAnalysis (1.0.0) current version: 1.1.0 »

Source Notebook

An interactive plot for the areas inside the rose curve

Contributed by: Garrett Dubofsky, Wolfram|Alpha Math Team

ResourceFunction["RoseCurveAnalysis"][a,n]

returns a plot with selectable areas of the rose curve with polar formula .

ResourceFunction["RoseCurveAnalysis"][a,n,prop]

returns an interactive plot along with values of the properties in prop.

Details and Options

A rose curve is a class of curves defined by the equation in polar coordinates. When n is a rational number, the periodicity of the Sin function means that the rose curve forms a closed loop after at most one period of the function. This is what is referred to as a rose curve.
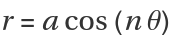
In some cases, the polar equation of the rose curve is given as . Although ResourceFunction["RoseCurveAnalysis"] does not have the option to switch between forms, the cosine form is equivalent to rotating the sine form by 90 degrees counterclockwise.
The amplitude a can be any real value whereas the angle coefficient n must be a nonzero rational.
For the purposes of this function, a "petal" of a rose curve is defined as a minimal (possibly self intersecting) segment of the curve that starts and ends at the origin and does not pass through the origin otherwise. A "subpetal" is a closed region within the rose curve.
"TotalArea" refers to an area calculated by integration, which counts overlapped sections multiple times. By contrast, "SurfaceArea" counts each selected area once.
The following values of prop are supported for both integer and rational values of n:
"Equation" equation of the rose curve
"Plot" plot of the rose curve
"PetalPlot" plot of a single petal
"PetalCount" number of petals
"PetalTotalAreaFormula" formula for the total area of a single petal
"PetalTotalArea" total area of a single petal
"InactiveTotalAreaIntegral" inactive double integral for the total area of the rose curve
"InactiveTotalAreaSingleIntegral" inactive single integral for the total area of the rose curve
"TotalAreaFormula" formula for the total area of a rose curve (for rational n, rewrite n as the reduced fration p/q)
"TotalArea" total area of the rose curve
"TotalAreaPlot" plot of the rose curve where darker hues correspond to overlapped sections
"PetalArcLength" arc length of a single petal
"ArcLength" arc length of the rose curve over one full period
"IntersectionCount" number of times the rose curve self-intersects
"ClosedDomain" the interval of angles where the rose curve makes a complete cycle
All all properties associated with the given value of n
The following values of prop are intended for rational values of n but can be called for integer values of n as well:
"PetalSurfaceAreaFormula" formula for the surface area of a single petal
"PetalSurfaceArea" surface area of a single petal
"InactiveSurfaceAreaIntegral" inactive double integral for the surface area of the rose curve
"InactiveSurfaceAreaSingleIntegral" inactive single integral for the surface area of the rose curve
"SurfaceAreaFormula" formula for the surface area the rose curve (n is expressed as the reduced fraction p/q)
"SurfaceArea" surface area of the rose curve
"OuterCurveEquation" piecewise function for the outline of the rose curve
"OuterCurvePlot" plot of the outline of the rose curve
Multiple values of prop can be specified using a list. The order of the input properties is mirrored in the output.
The same options as ParametricPlot and PolarPlot are supported, as well as the following:
"Point" determines the initial shaded region (default value is {0.1,0.1})
"ShowPetal" bolds the petal containing the shaded region

Examples

Basic Examples (2) 

Plot the given rose curve with clickable subpetals:

In[1]:=
ResourceFunction["RoseCurveAnalysis"][1, 4/3]
Out[1]=

Get the number of petals, surface area, and total area alongside the interactive plot:

In[2]:=
ResourceFunction["RoseCurveAnalysis"][1, 7/6, {"PetalCount", "SurfaceArea", "TotalArea"}]
Out[2]=

Scope (1) 

Negative values of a and decimal forms of n are acceptable and are rationalized internally to produce exact results:

In[3]:=
ResourceFunction["RoseCurveAnalysis"][-4, 0.8, "Equation"]
Out[3]=

Options (4) 

Default PolarPlot and ParametricPlot options apply to each graphic:

In[4]:=
ResourceFunction["RoseCurveAnalysis"][1, 7/8, {"Plot", "PetalPlot", "OuterCurvePlot", "TotalAreaPlot"}, Axes -> False, PlotStyle -> {Thick, Hue[.55]}, MeshStyle -> {Blue, Opacity[1]}, BoundaryStyle -> Black]
Out[4]=

Change the initial point:

In[5]:=
ResourceFunction["RoseCurveAnalysis"][1, 4/3, "Point" -> {-0.8, -0.5}]
Out[473]=

Bold the petal containing the shaded region:

In[474]:=
ResourceFunction["RoseCurveAnalysis"][2, 3/7, "ShowPetal" -> True, PlotStyle -> Red]
Out[474]=

Use PlotRange to view small regions:

In[475]:=
{ResourceFunction["RoseCurveAnalysis"][1, 13/15, "Point" -> {0.05, 0.035}], ResourceFunction["RoseCurveAnalysis"][1, 13/15, PlotRange -> 0.15, "Point" -> {0.05, 0.035}]}
Out[904]=

Applications (4) 

Generate all the subpetal areas:

In[905]:=
{ResourceFunction["RoseCurveAnalysis"][2, 4/3, "Point" -> {0.5, 0.1}], ResourceFunction["RoseCurveAnalysis"][2, 4/3], ResourceFunction["RoseCurveAnalysis"][2, 4/3, "Point" -> {1, 1.5}]}
Out[906]=

Determine the number of petals:

In[907]:=
RoseCurveProperties[2, 4/3, "PetalCount"]
Out[907]=

Click to copy the selected areas and sum them together, multiplying by the number of petals:

In[908]:=
Simplify[8*(1/8*(-3 Sqrt[3] + 2 \[Pi]) + (3 Sqrt[3])/8 + (3 Sqrt[3])/ 8)]
Out[908]=

As desired, this is equivalent to the surface area of the rose curve:

In[909]:=
RoseCurveProperties[2, 4/3, "SurfaceArea"]
Out[909]=

Possible Issues (4) 

The ImageSize option has no effect:

In[910]:=
ResourceFunction["RoseCurveAnalysis"][3, 6/5, "Plot", ImageSize -> 1]
Out[910]=

For nonnumerical values of a, the function is left unevaluated:

In[911]:=
ResourceFunction["RoseCurveAnalysis"][x, 5/4]
Out[911]=

For negative, irrational, or nonnumerical values of n, the function is left unevaluated:

In[912]:=
ResourceFunction["RoseCurveAnalysis"][1, \[Pi]]
Out[912]=

When no available property is called, the function is left unevaluated:

In[913]:=
ResourceFunction["RoseCurveAnalysis"][1, 2/3, "Ack"]
Out[913]=

Neat Examples (2) 

For some rose curves, the selected areas are not unique:

In[914]:=
{ResourceFunction["RoseCurveAnalysis"][2, 5/6, "Point" -> {0.5, 0.75}], ResourceFunction["RoseCurveAnalysis"][2, 5/6, "Point" -> {1, 1.25}]}
Out[914]=

When n=1/2, the subpetals have very convenient values:

In[915]:=
ResourceFunction["RoseCurveAnalysis"][1, 1/2, "Point" -> {0.5, 0}]
Out[915]=

Version History

  • 1.1.0 – 10 May 2022
  • 1.0.0 – 04 January 2022

Related Resources

Author Notes

To view the full source code for RoseCurveProperties, evaluate the following:

In[1]:=
SystemOpen[ FileNameJoin[{DirectoryName[FindFile["ResourceFunctionHelpers`"]], "RoseCurveProperties.wl"}]]

License Information