Scope (3)
There are two modes of making random mandalas: (i) single-mandala mode and (ii) multi-mandala mode. The multi-mandala mode is activated by giving the "Radius" option a list of positive reals.
Here are gray-level and colorized mandalas generated with the single-mandala mode:
Here are gray-level and colorized mandalas generated with a multi-mandala mode:
Options (12)
ColorFunction (2)
The function given to ColorFunction is run over Range[0,1,0.1] the obtained colors are used to colorize the mandala. By default no colorizing is done, ColorFunction->None.
ColorFunction can also take strings that are color schemes known by ColorData.
Here is a list of colorized mandalas using single-mandala mode:
Here are mandalas generated using multi-mandala mode:
ConnectingFunction (1)
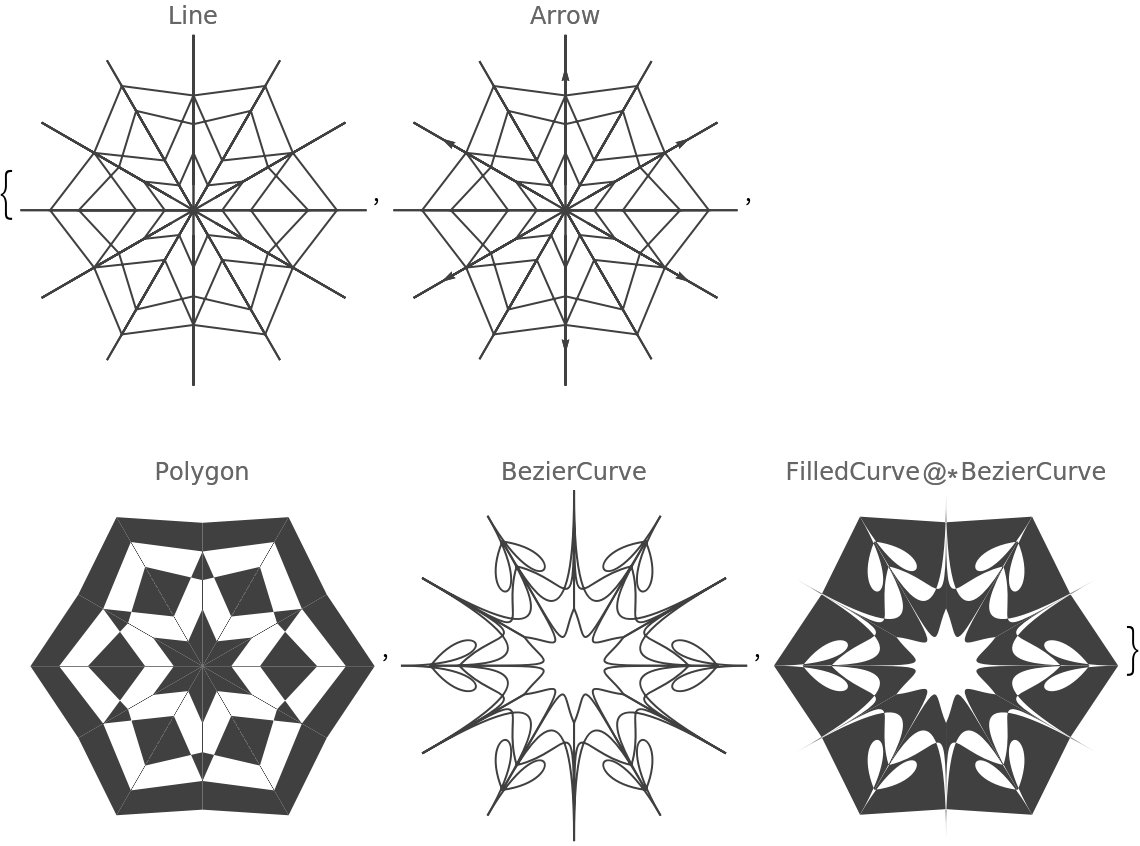
The option "ConnectingFunction" specifies which graphics primitive to be used over the seed segment points:
EdgeForm (1)
The option EdgeForm specifies directives for the edges of polygons or other filled graphics objects:
FaceForm (1)
The option FaceForm specifies directives for the faces of polygons or other filled graphics objects:
KeepGridPoints (1)
The option "KeepGridPoints" specifies should the points used to generate the seed segment be kept or not:
NumberOfElements (1)
The option "NumberOfElements" controls how may graphics elements are in the seed segment:
If the value of “NumberOfElements” is Automatic in single-mandala mode 6 elements are used, and in multi-mandala mode 3 elements are used (for each mandala.)
Radius (2)
In single-mandala mode the option "Radius" specifies the radius of the seed segment and the mandala:
If the value given to “Radius” is a list of positive numbers then multi-mandala mode is used.
If "Radius"→{r1,…,rk}, then for each ri is made a mandala with radius ri and the mandalas are drawn upon each other according to their radii order:
Using the option ColorFunction colorized mandalas are obtained:
RotationalSymmetryOrder (2)
The "RotationalSymmetryOrder" option specifies how many copies of the seed segment comprise the mandala:
If both "Radius" and “RotationalSymmetryOrder” is given given lists of numbers then the corresponding elements in those are paired to make the specifications of the colorized mandalas:
SymmetricSeed (1)
The option "SymmetricSeed" specifies should the seed segment be symmetric or not:
Properties and Relations (2)
Using combinations of settings for ColorFunction, EdgeForm, and FaceForm can produce certain more nuanced mandala effects than, say, just using ColorFunction:
RandomMandala can be used in more or less the same way as the resource function RandomScribble. Here, RandomMandala is used with the resource function TexturizePolygons:
Here, the resource function RandomScribble is used with the resource function TexturizePolygons:
Possible Issues (1)
In general, the rotational symmetry order should be an integer, but for didactic purposes it is permitted to be a positive real. If the specified rotational symmetry order is not an integer, then the produced mandalas will appear “open”:

![SeedRandom[1];
ResourceFunction["RandomMandala"]["RotationalSymmetryOrder" -> 7, "Radius" -> 12, "SymmetricSeed" -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/34697732aba955c3.png)


![SeedRandom[54929];
Table[ResourceFunction["RandomMandala"]["Radius" -> 10, ColorFunction -> ColorData["Rainbow"]], 4]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/7d6575d0008fbc05.png)



![Table[SeedRandom[17]; ResourceFunction["RandomMandala"][ColorFunction -> ColorData[cf], PlotLabel -> cf], {cf, {"Rainbow", "SouthwestColors", "BrightBands",
"DeepSeaColors"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/2ad490d20d38270d.png)

![Table[SeedRandom[74]; ResourceFunction["RandomMandala"]["Radius" -> {7, 6, 4}, ColorFunction -> cf, PlotLabel -> cf], {cf, {"Rainbow", "SouthwestColors", "BrightBands",
"DeepSeaColors"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/5a562a48b660b33b.png)

![Table[(SeedRandom[263]; ResourceFunction["RandomMandala"]["ConnectingFunction" -> cf, PlotLabel -> cf]), {cf, {Line, Arrow, Polygon, BezierCurve, FilledCurve@*BezierCurve}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/3952de45c5d002a3.png)
![SeedRandom[42];
ResourceFunction["RandomMandala"]["Radius" -> 8, "RotationalSymmetryOrder" -> 5, "ConnectingFunction" -> FilledCurve@*BezierCurve, EdgeForm -> {Red, Thick}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/05c2fb40c0004b13.png)

![Table[(SeedRandom[8]; ResourceFunction["RandomMandala"]["Radius" -> {6, 8, 4}, ColorFunction -> "Rainbow", "ConnectingFunction" -> FilledCurve@*BezierCurve, PlotLabel -> Row[{"Opacity:", Spacer[3], op}], FaceForm -> {Opacity[op]}]), {op, {0.4, 0.6, 1}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/7ff354d033e80e23.png)

![Table[(SeedRandom[163]; ResourceFunction["RandomMandala"]["KeepGridPoints" -> k, "NumberOfSeedElements" -> 3, "RotationalSymmetryOrder" -> 6, PlotLabel -> k]), {k, {True, False}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/1d62874a8be8f86b.png)
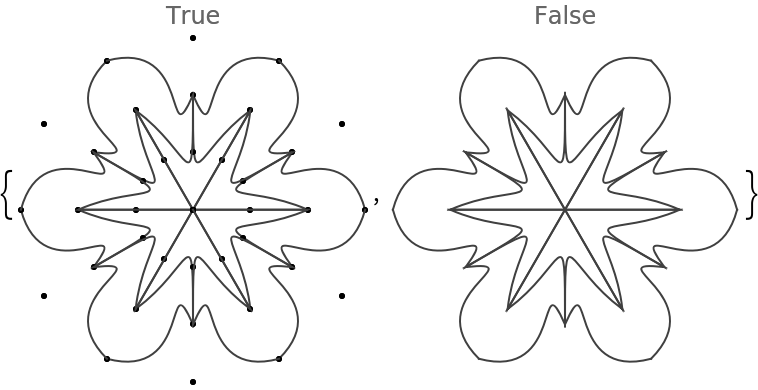
![Table[(SeedRandom[163]; ResourceFunction["RandomMandala"]["KeepGridPoints" -> k, "NumberOfSeedElements" -> 5, "RotationalSymmetryOrder" -> 6, PlotLabel -> k]), {k, {True, False}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/63c712003b82a1db.png)
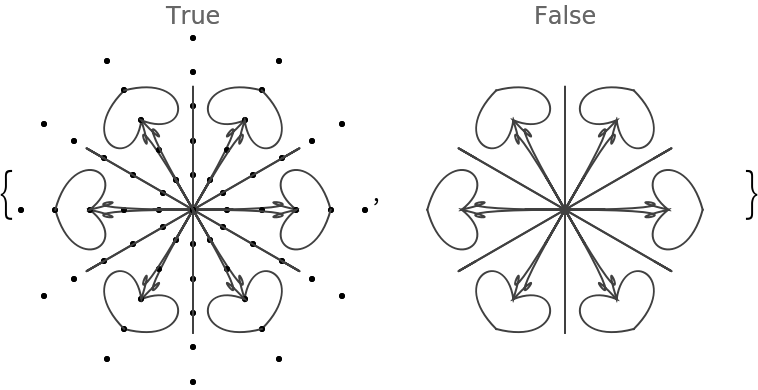
![Table[(SeedRandom[200]; ResourceFunction["RandomMandala"]["NumberOfSeedElements" -> n, "RotationalSymmetryOrder" -> 3, PlotLabel -> Row[{"n:", Spacer[2], n}]]), {n, 1, 6}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/0e3ef63f731c55e3.png)
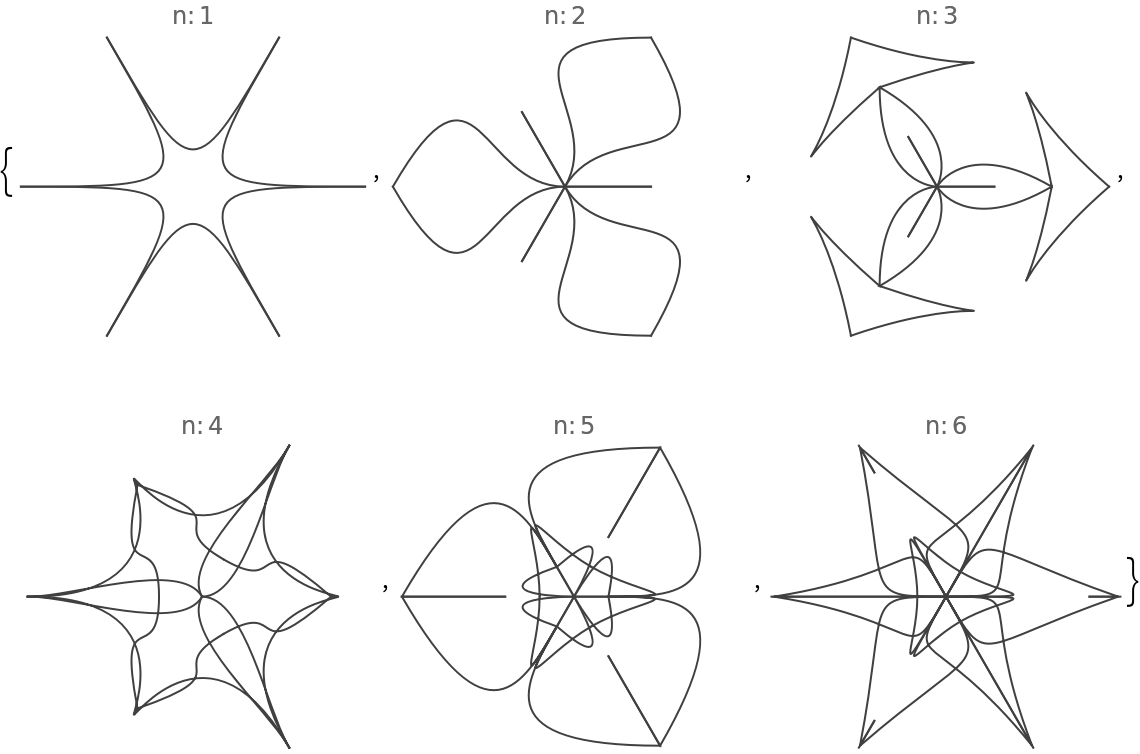
![Table[(SeedRandom[200]; ResourceFunction["RandomMandala"]["NumberOfSeedElements" -> n, "RotationalSymmetryOrder" -> 3, PlotLabel -> Row[{"n:", Spacer[2], n}]]), {n, 5, 20, 5}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/237bb4c794e75bfe.png)
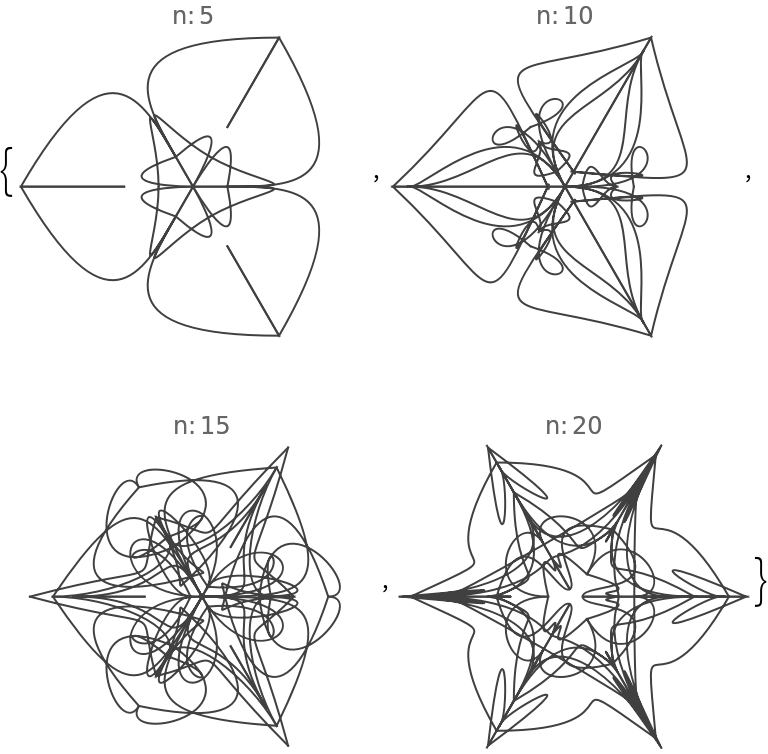
![Table[(SeedRandom[226]; ResourceFunction["RandomMandala"]["Radius" -> r, PlotLabel -> Row[{"radius:", Spacer[2], r}], Frame -> True]), {r, 5, 20, 5}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/0ae8e513ccf4a7e4.png)
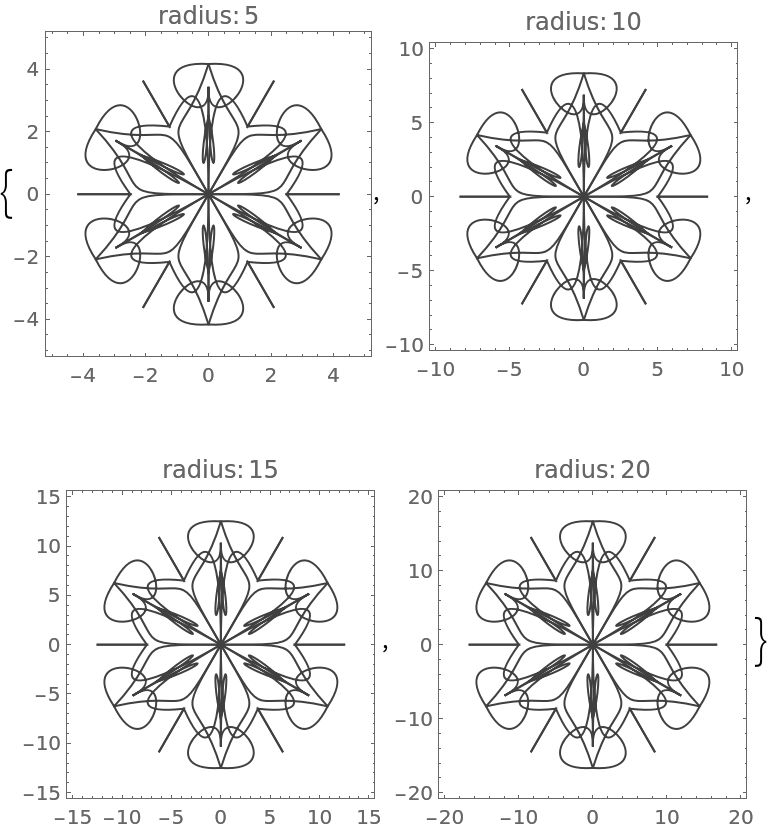


![Table[(SeedRandom[122]; ResourceFunction["RandomMandala"]["RotationalSymmetryOrder" -> a, PlotLabel -> Row[{"order:", Spacer[2], a}]]), {a, {2, 3, 4, 6}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/5b3043e2f6567eeb.png)

![Table[(SeedRandom[122]; ResourceFunction["RandomMandala"]["RotationalSymmetryOrder" -> a, "SymmetricSeed" -> False, PlotLabel -> Row[{"order:", Spacer[2], a}]]), {a, {2, 3, 4, 6}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/6e0d664c95c9afc3.png)

![Table[
SeedRandom[122];
ResourceFunction["RandomMandala"]["Radius" -> {8, 4}, "RotationalSymmetryOrder" -> rs, "ConnectingFunction" -> FilledCurve@*BezierCurve, ColorFunction -> "Rainbow", FaceForm -> {Opacity[0.7]}, EdgeForm -> {White, Opacity[1]}, PlotLabel -> Row[{"order:", Spacer[2], rs}]], {rs, {{4, 2}, {6, 3}, {5, 10}}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/0a3603b791e30114.png)

![Table[(SeedRandom[122]; ResourceFunction["RandomMandala"]["SymmetricSeed" -> s, PlotLabel -> s]), {s, {True, False}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/195e75ae5f604e54.png)
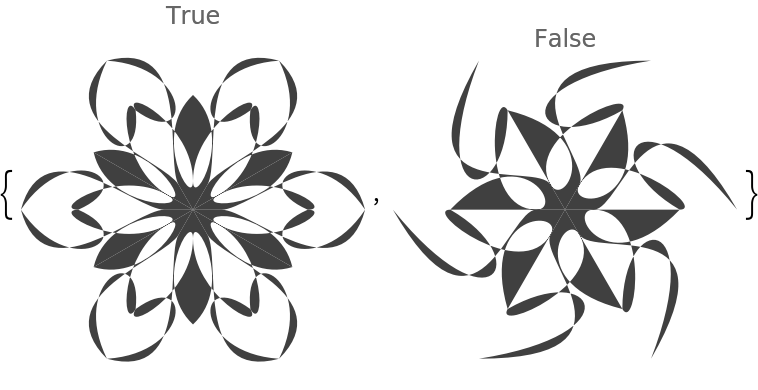
![Table[
SeedRandom[89];
ResourceFunction["RandomMandala"]["Radius" -> {8, 6, 4}, "RotationalSymmetryOrder" -> {12, 6, 3}, "ConnectingFunction" -> FilledCurve@*BezierCurve, ColorFunction -> "RustTones", ImageSize -> 300, opts], {opts, {{FaceForm -> {Opacity[0.7]}, EdgeForm -> {White, Thickness[0.006], Opacity[1]}}, {}}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/3f1156d5f33b08ee.png)

![SeedRandom[5353];
ResourceFunction["TexturizePolygons"][{"Dodecahedron", "Net"}, Table[ResourceFunction["RandomMandala"][
ColorFunction -> ColorData["Rainbow"]], 4], "Granularity" -> "Polygon"]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/063e0c9c6c10872a.png)
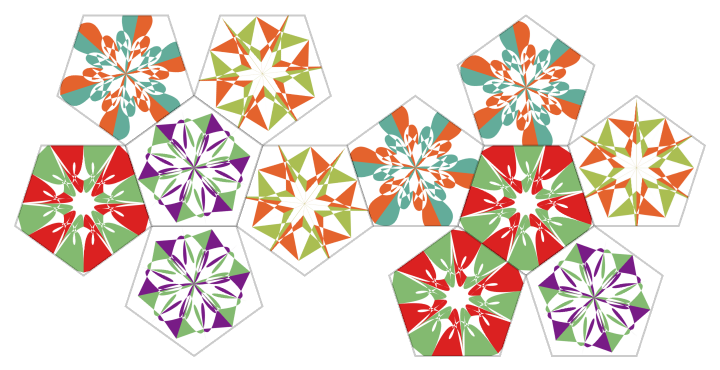
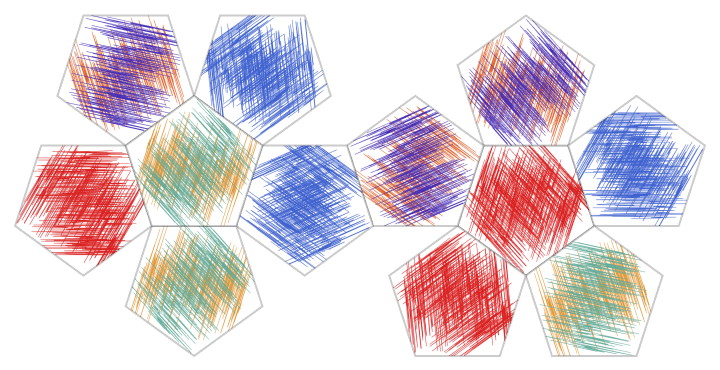
![SeedRandom[2323];
ResourceFunction["TexturizePolygons"][{"Dodecahedron", "Net"}, Table[ResourceFunction["RandomScribble"][
"NumberOfStrokes" -> RandomInteger[{600, 820}, 2], ColorFunction -> ColorData["Rainbow"]], 4], "Granularity" -> "Polygon"]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/653b70471f76e335.png)


![SeedRandom[342]; Multicolumn[
Table[ResourceFunction["RandomMandala"][
"RotationalSymmetryOrder" -> RandomChoice[{3, 6, 12}], "SymmetricSeed" -> RandomChoice[{True, False}], ImageSize -> Tiny],
36], 6]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/606255c75aa8bfd2.png)

![SeedRandom[474]; Multicolumn[
Table[ResourceFunction["RandomMandala"][
"Radius" -> Reverse[Range[RandomChoice[{3, 4, 5, 6}]]], "NumberOfSeedElements" -> RandomChoice[{2, 3, 4}], "RotationalSymmetryOrder" -> RandomChoice[{3, 4, 5, 6, 7}], ColorFunction -> "DarkRainbow", "ConnectingFunction" -> FilledCurve@*BezierCurve, "SymmetricSeed" -> True, FaceForm -> {Opacity[0.7]}, EdgeForm -> {LightBlue, Opacity[1]}, ImageSize -> 150], 25], 6]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/72957ca251953598.png)

![n = 36;
Magnify[Multicolumn[
Map[BlockRandom[SeedRandom[24]; ResourceFunction["RandomMandala"]["RotationalSymmetryOrder" -> #,
ColorFunction -> ColorData["DeepSeaColors"]]] &, RandomReal[{2, 4}, n]], 6], 0.5]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/5e75c0557f4f8696.png)

![SeedRandom[6567];
mandalas = Table[ResourceFunction["RandomMandala"][], 36];
Magnify[mandalas, 0.3]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/52c425e9ebccf38d.png)

![AbsoluteTiming[
mandalaImages = Map[Image[#, ImageSize -> {400, 400}, ColorSpace -> "Grayscale"] &,
mandalas];
]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/570c6f0d0affe8c0.png)
![SeedRandom[3488];
AbsoluteTiming[
directBlendingImages = Table[
RemoveBackground@
ImageAdjust[
Blend[Colorize[#, ColorFunction -> RandomChoice[{"IslandColors", "FruitPunchColors", "AvocadoColors", "Rainbow"}]] & /@ RandomChoice[mandalaImages, 4], RandomReal[1, 4]]], 12];
]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2-1-0/117088adb8a2627d.png)
