Scope (2)
There are two modes of making random mandalas: (i) single-mandala mode and (ii) multi-mandala mode. The multi-mandala mode is activated by giving the "Radius" option a list of positive reals.
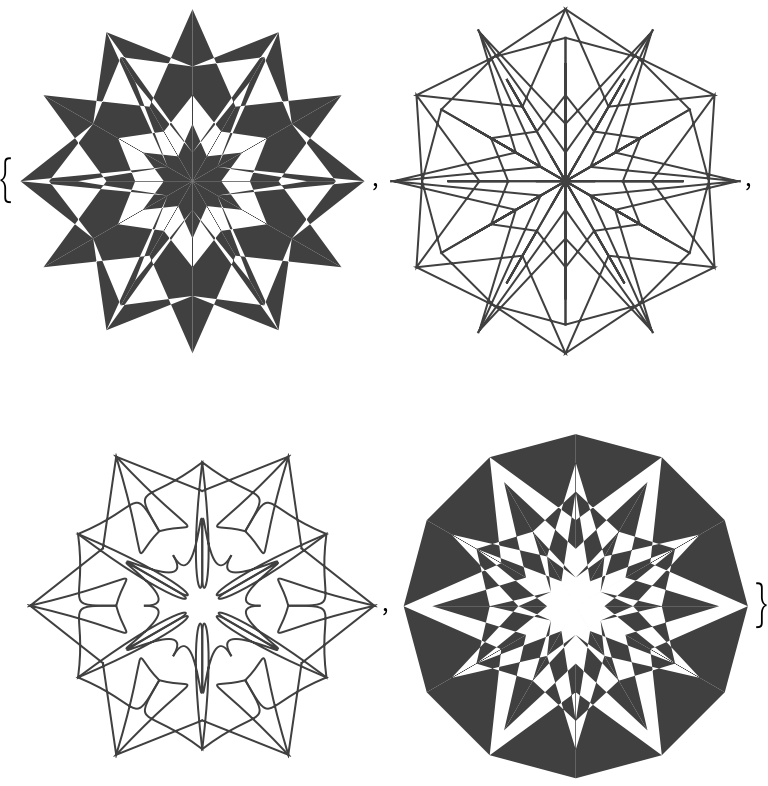
Here are gray mandalas generated with the single-mandala mode:
Here are colorized mandalas generated with the single-mandala mode:
Here are gray mandalas generated with a multi-mandala mode:
Here are colorized mandalas generated with a multi-mandala mode:
Options (16)
ColorFunction (2)
The function given to ColorFunction is run over Range[0,1,0.1] and the obtained colors are used to colorize the mandala. By default no colorizing is done and ColorFunction→None.
ColorFunction can also take strings that are color schemes known by ColorData.
Here is a list of colorized mandalas using single-mandala mode:
Here are mandalas generated using multi-mandala mode:
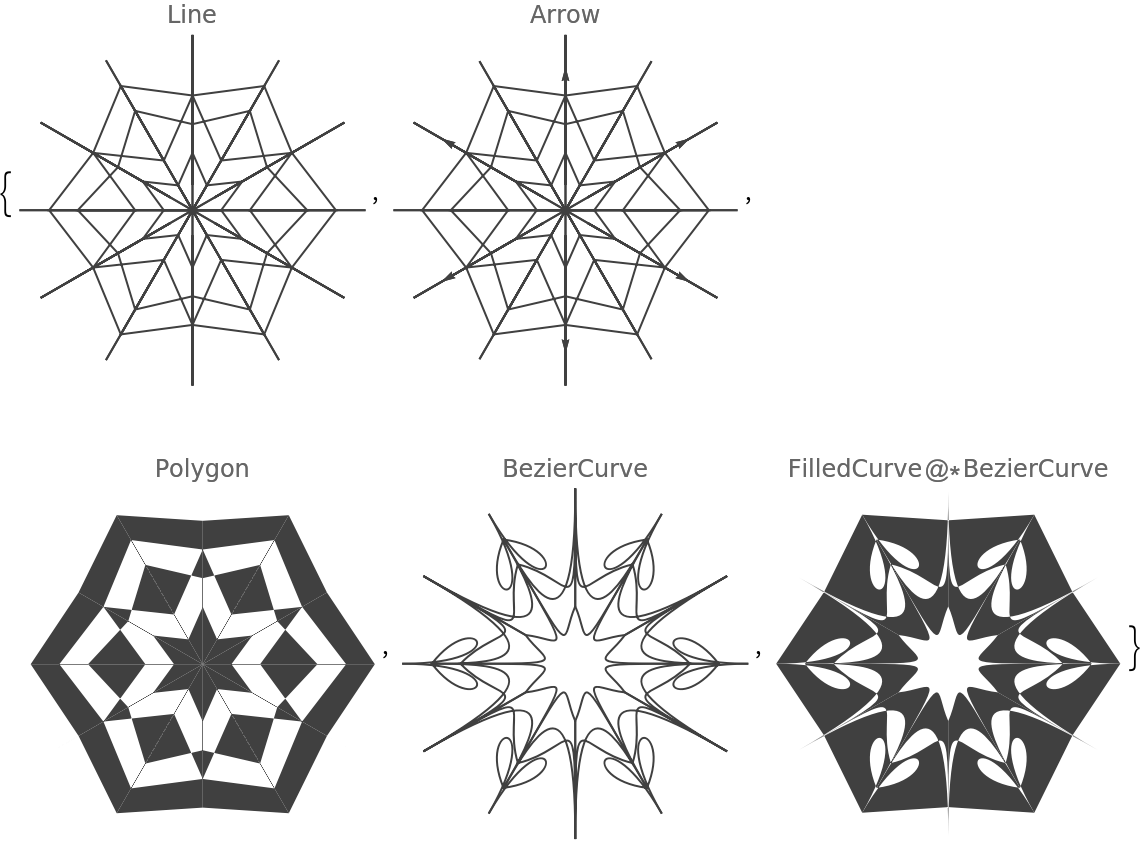
ConnectingFunction (1)
The option "ConnectingFunction" specifies which graphics primitive to use over the seed segment points:
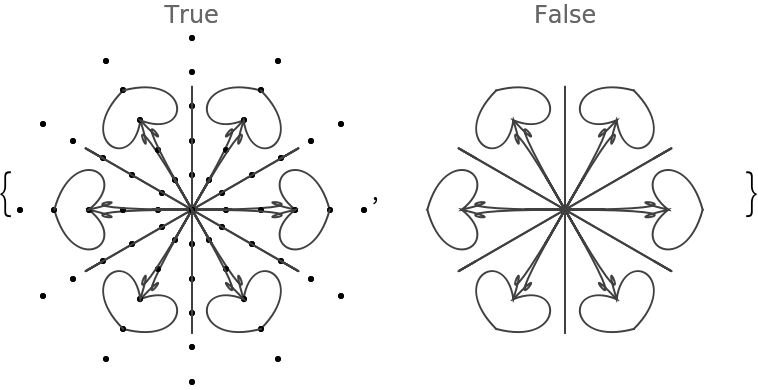
EdgeForm (1)
The option EdgeForm specifies directives for the edges of polygons or other filled graphics objects:
FaceForm (1)
The option FaceForm specifies directives for the faces of polygons or other filled graphics objects:
KeepGridPoints (1)
The option "KeepGridPoints" specifies whether the points used to generate the seed segment should be kept:
NumberOfElements (1)
The option "NumberOfElements" controls how may graphics elements are in the seed segment:
If the value of "NumberOfElements" is Automatic in single-mandala mode, 6 elements are used; in multi-mandala mode, 3 elements are used (for each mandala).
Radius (2)
In single-mandala mode the option "Radius" specifies the radius of the seed segment and the mandala:
If the value given to "Radius" is a list of positive numbers, then multi-mandala mode is used.
If "Radius"→{r1,…,rk}, then for each ri, a mandala is made with radius ri and the mandalas are drawn upon each other according to their radii order:
Using the option ColorFunction, colorized mandalas are obtained:
RotationalSymmetryOrder (3)
The "RotationalSymmetryOrder" option specifies how many copies of the seed segment comprise the mandala:
If both "Radius" and "RotationalSymmetryOrder" are given lists of numbers, then the corresponding elements in those are paired to make the specifications of the colorized mandalas:
If “Radius” is set to Automatic and “RotationalSymmetryOrder” is given a list of positive numbers with length ρ, then the value or “Radius” becomes a list of corresponding length with the formula Reverse[Rescale[Range[Length[Flatten[ρ]]],{0,10}]]. Here are examples:
SeedFunction (3)
The option "SeedFunction" specifies the function for drawing mandala's seed segment. If the value is Automatic, then the seed segment is drawn by taking into account the values of the options "Radius", "NumberOfSeedElements", "KeepGridPoints" and "ConnectingFunction".
Here is a custom seed function that places circles or disks at random points within the segment that corresponds to radius and angle:
Here are single-mandala mode mandalas made with the custom seed segment function defined above:
Here are multi-mandala mode colorized mandalas (with two seed elements and randomly selected connecting functions):
SymmetricSeed (1)
The option "SymmetricSeed" specifies whether the seed segment should be symmetric:
Neat Examples (8)
Random mandalas (3)
A table of random mandalas:
A table of random colorized mandalas:
A table of "open" colorized mandalas:
Colored mandala images by blending (4)
Make a list of random mandalas:
Make images of the generated mandala graphics:
Pick mandala images at random and blend them using a set of coloring schemes:
Make a collage:
Mandalas made with random scribbles (1)
Here are mandalas made with the repository function RandomScribble:

![SeedRandom[1];
ResourceFunction["RandomMandala"]["RotationalSymmetryOrder" -> 7, "Radius" -> 12, "SymmetricSeed" -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/0c06d0342c15f6d7.png)

![SeedRandom[54929];
Table[ResourceFunction["RandomMandala"]["Radius" -> 10, ColorFunction -> ColorData["Rainbow"]], 4]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/07090c5c1a9177d9.png)



![Table[SeedRandom[17]; ResourceFunction["RandomMandala"][ColorFunction -> ColorData[cf], PlotLabel -> cf], {cf, {"Rainbow", "SouthwestColors", "BrightBands",
"DeepSeaColors"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/6cb705c387257d43.png)

![Table[SeedRandom[74]; ResourceFunction["RandomMandala"]["Radius" -> {7, 6, 4}, ColorFunction -> cf, PlotLabel -> cf], {cf, {"Rainbow", "SouthwestColors", "BrightBands",
"DeepSeaColors"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/13576343be9edaa9.png)

![Table[(SeedRandom[263]; ResourceFunction["RandomMandala"]["ConnectingFunction" -> cf, PlotLabel -> cf]), {cf, {Line, Arrow, Polygon, BezierCurve, FilledCurve@*BezierCurve}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/0b9f050822551a9f.png)
![SeedRandom[42];
ResourceFunction["RandomMandala"]["Radius" -> 8, "RotationalSymmetryOrder" -> 5, "ConnectingFunction" -> FilledCurve@*BezierCurve, EdgeForm -> {Red, Thick}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/53e47b13b37c00a0.png)

![Table[(SeedRandom[8]; ResourceFunction["RandomMandala"]["Radius" -> {6, 8, 4}, ColorFunction -> "Rainbow", "ConnectingFunction" -> FilledCurve@*BezierCurve, PlotLabel -> Row[{"Opacity:", Spacer[3], op}], FaceForm -> {Opacity[op]}]), {op, {0.4, 0.6, 1}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/187f7adb31606bac.png)

![Table[(SeedRandom[163]; ResourceFunction["RandomMandala"]["KeepGridPoints" -> k, "NumberOfSeedElements" -> 3, "RotationalSymmetryOrder" -> 6, PlotLabel -> k]), {k, {True, False}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2cb211c29054c427.png)
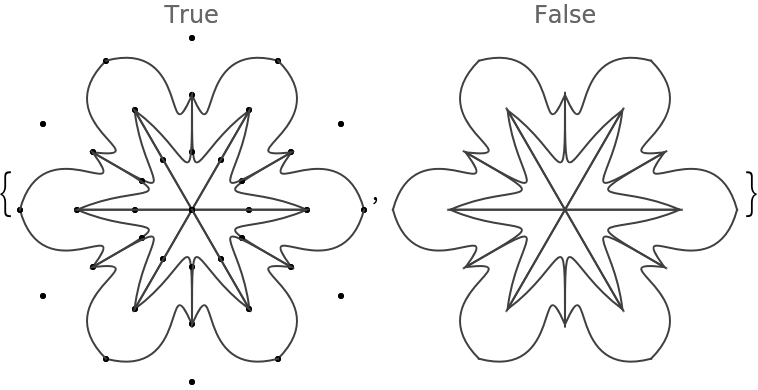
![Table[(SeedRandom[163]; ResourceFunction["RandomMandala"]["KeepGridPoints" -> k, "NumberOfSeedElements" -> 5, "RotationalSymmetryOrder" -> 6, PlotLabel -> k]), {k, {True, False}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/11a6cded4b641834.png)
![Table[(SeedRandom[200]; ResourceFunction["RandomMandala"]["NumberOfSeedElements" -> n, "RotationalSymmetryOrder" -> 3, PlotLabel -> Row[{"n:", Spacer[2], n}]]), {n, 1, 6}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/31115c3d94142187.png)
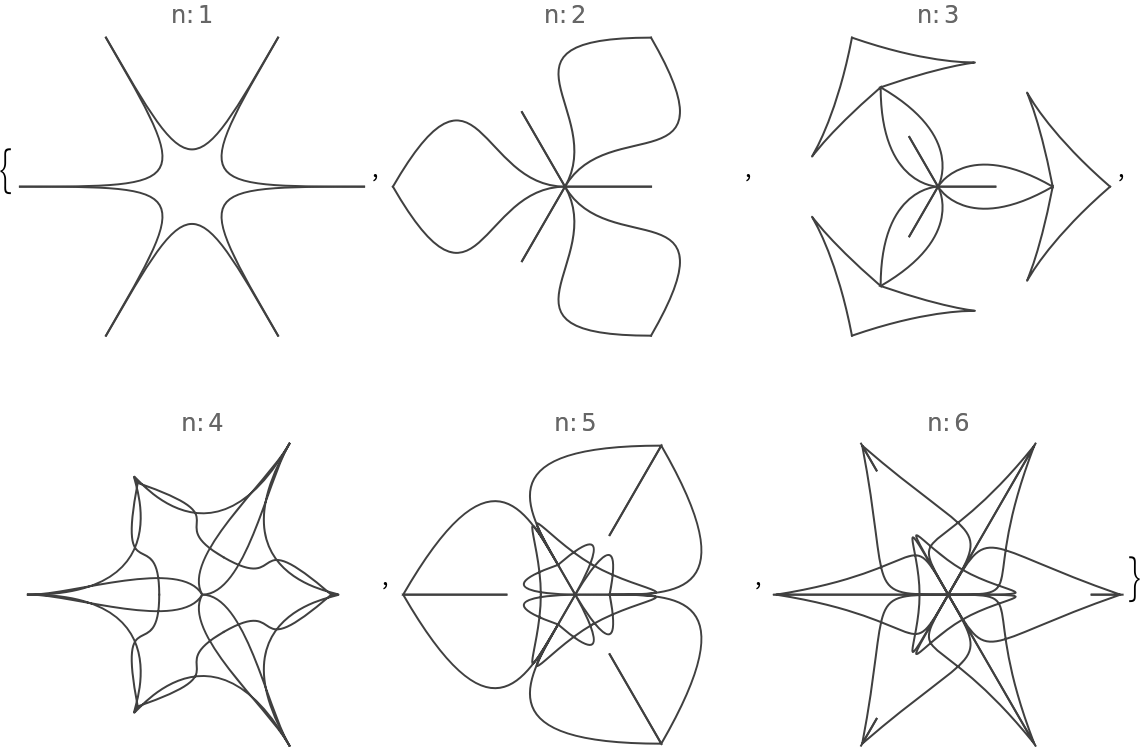
![Table[(SeedRandom[200]; ResourceFunction["RandomMandala"]["NumberOfSeedElements" -> n, "RotationalSymmetryOrder" -> 3, PlotLabel -> Row[{"n:", Spacer[2], n}]]), {n, 5, 20, 5}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/0eab17e9b71f8c52.png)
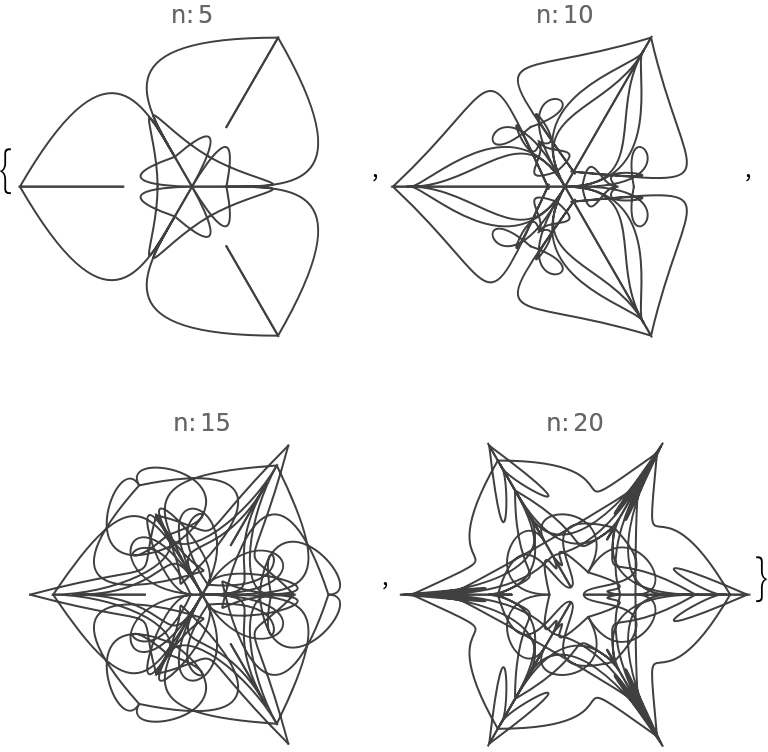
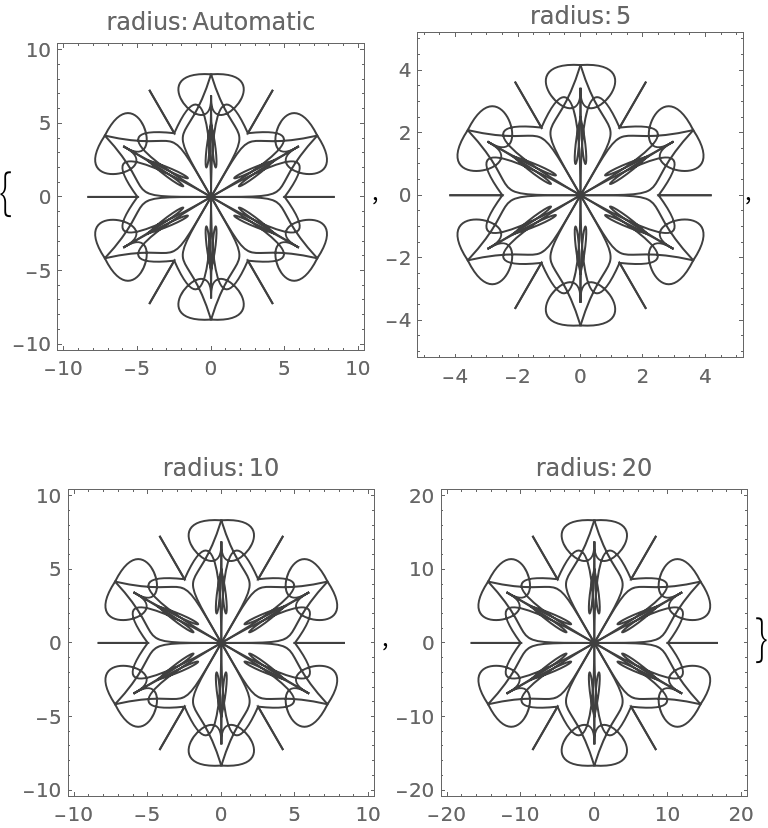
![Table[(SeedRandom[226]; ResourceFunction["RandomMandala"]["Radius" -> r, PlotLabel -> Row[{"radius:", Spacer[2], r}], Frame -> True]), {r, {Automatic, 5, 10, 20}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/4a214422e45e2b49.png)


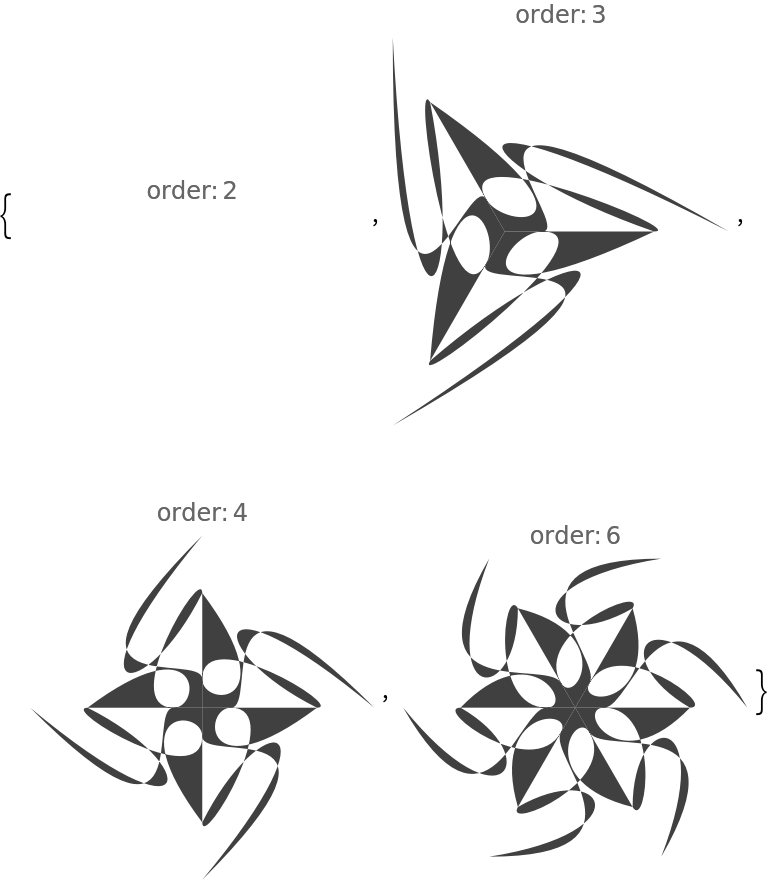
![Table[(SeedRandom[122]; ResourceFunction["RandomMandala"]["RotationalSymmetryOrder" -> a, PlotLabel -> Row[{"order:", Spacer[2], a}]]), {a, {2, 3, 4, 6}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/41818c3748735607.png)

![Table[(SeedRandom[122]; ResourceFunction["RandomMandala"]["RotationalSymmetryOrder" -> a, "SymmetricSeed" -> False, PlotLabel -> Row[{"order:", Spacer[2], a}]]), {a, {2, 3, 4, 6}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/5445950160dd68e9.png)
![Table[
SeedRandom[122];
ResourceFunction["RandomMandala"]["Radius" -> {8, 4}, "RotationalSymmetryOrder" -> rs, "ConnectingFunction" -> FilledCurve@*BezierCurve, ColorFunction -> "Rainbow", FaceForm -> {Opacity[0.7]}, EdgeForm -> {White, Opacity[1]}, PlotLabel -> Row[{"order:", Spacer[2], rs}]], {rs, {{4, 2}, {6, 3}, {5, 10}}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/27b530a848dccb07.png)

![Table[
SeedRandom[122];
ResourceFunction["RandomMandala"]["Radius" -> Automatic, "RotationalSymmetryOrder" -> rs, "ConnectingFunction" -> FilledCurve@*BezierCurve, ColorFunction -> "SouthwestColors", FaceForm -> {Opacity[0.7]}, EdgeForm -> {White, Opacity[1]}, PlotLabel -> Row[{"order:", Spacer[2], rs}]], {rs, {5, {4, 2}, {9, 6, 3}}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/1eaa69dc826f2580.png)

![Clear[CustomSeed];
CustomSeed[radius_, angle_, n_Integer : 10, connectingFunc_ : Polygon,
keepGridPoints_ : False, opts : OptionsPattern[]] :=
Block[{cf = connectingFunc},
If[! MemberQ[{Circle, Disk}, cf], cf = Circle];
Flatten@Table[
cf[p, radius*RandomReal[{0.01, 0.2}]],
{p, RandomPoint[Disk[{0, 0}, radius, {0, angle}], n]}]
];](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/46b51c1ad88196f4.png)
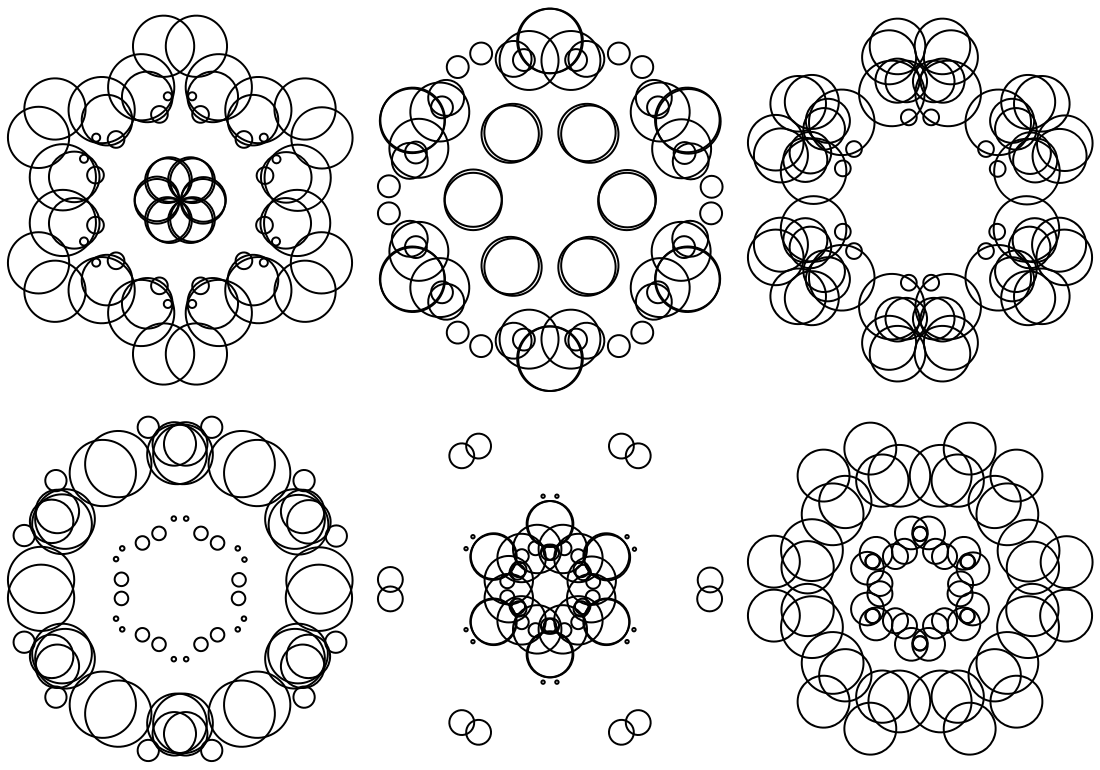
![SeedRandom[344];
Grid@Table[
ResourceFunction["RandomMandala"]["Radius" -> {10, 6, 3}, "SeedFunction" -> CustomSeed, "ConnectingFunction" -> RandomChoice[{Circle, Disk}], "NumberOfSeedElements" -> 2, "ColorFunction" -> "DarkRainbow"], {2}, {3}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/3d474ff9f35a11e3.png)

![Table[(SeedRandom[122]; ResourceFunction["RandomMandala"]["SymmetricSeed" -> s, PlotLabel -> s]), {s, {True, False}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/65e83f313c65c8cc.png)
![Table[
SeedRandom[89];
ResourceFunction["RandomMandala"]["Radius" -> {8, 6, 4}, "RotationalSymmetryOrder" -> {12, 6, 3}, "ConnectingFunction" -> FilledCurve@*BezierCurve, ColorFunction -> "RustTones", ImageSize -> 300, opts], {opts, {{FaceForm -> {Opacity[0.7]}, EdgeForm -> {White, Thickness[0.006], Opacity[1]}}, {}}}]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/79d3a46180a17f7e.png)

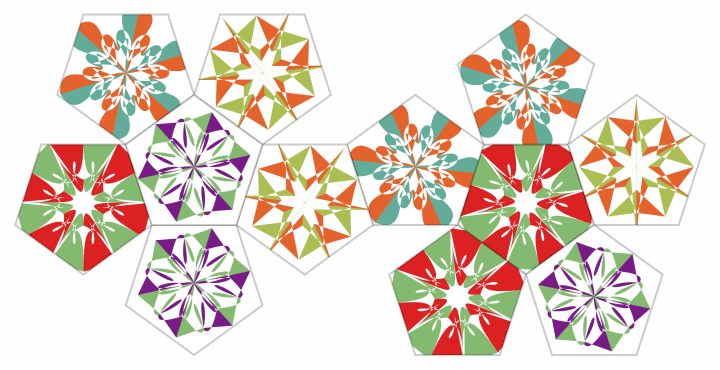
![SeedRandom[5353];
ResourceFunction["TexturizePolygons"][{"Dodecahedron", "Net"}, Table[ResourceFunction["RandomMandala"][
ColorFunction -> ColorData["Rainbow"]], 4], "Granularity" -> "Polygon"]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/75f6756418bcf11c.png)
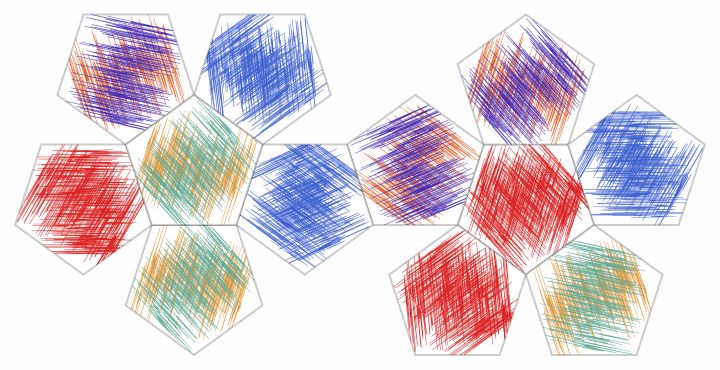
![SeedRandom[2323];
ResourceFunction["TexturizePolygons"][{"Dodecahedron", "Net"}, Table[ResourceFunction["RandomScribble"][
"NumberOfStrokes" -> RandomInteger[{600, 820}, 2], ColorFunction -> ColorData["Rainbow"]], 4], "Granularity" -> "Polygon"]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/3826737541ae6452.png)


![SeedRandom[342]; Multicolumn[
Table[ResourceFunction["RandomMandala"][
"RotationalSymmetryOrder" -> RandomChoice[{3, 6, 12}], "SymmetricSeed" -> RandomChoice[{True, False}], ImageSize -> Tiny],
36], 6]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/1629dbed058705a3.png)

![SeedRandom[474]; Multicolumn[
Table[ResourceFunction["RandomMandala"][
"Radius" -> Reverse[Range[RandomChoice[{3, 4, 5, 6}]]], "NumberOfSeedElements" -> RandomChoice[{2, 3, 4}], "RotationalSymmetryOrder" -> RandomChoice[{3, 4, 5, 6, 7}], ColorFunction -> "DarkRainbow", "ConnectingFunction" -> FilledCurve@*BezierCurve, "SymmetricSeed" -> True, FaceForm -> {Opacity[0.7]}, EdgeForm -> {LightBlue, Opacity[1]}, ImageSize -> 150], 25], 6]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/00bccc49b376819b.png)

![n = 36;
Magnify[Multicolumn[
Map[BlockRandom[SeedRandom[24]; ResourceFunction["RandomMandala"]["RotationalSymmetryOrder" -> #,
ColorFunction -> ColorData["DeepSeaColors"]]] &, RandomReal[{2, 4}, n]], 6], 0.5]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/7a44be17ca8b0d03.png)

![SeedRandom[6567];
mandalas = Table[ResourceFunction["RandomMandala"][], 36];
Magnify[mandalas, 0.3]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/066bd4d8bad235af.png)

![AbsoluteTiming[
mandalaImages = Map[Image[#, ImageSize -> {400, 400}, ColorSpace -> "Grayscale"] &,
mandalas];
]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2616c0bcb3d8efb5.png)
![SeedRandom[3488];
AbsoluteTiming[
directBlendingImages = Table[
RemoveBackground@
ImageAdjust[
Blend[Colorize[#, ColorFunction -> RandomChoice[{"IslandColors", "FruitPunchColors", "AvocadoColors", "Rainbow"}]] & /@ RandomChoice[mandalaImages, 4], RandomReal[1, 4]]], 12];
]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/2d3a5b01c21805b7.png)

![SeedRandom[67];
Clear[ScribblesSeed];
Options[ScribblesSeed] = Options[ResourceFunction["RandomScribble"]];
ScribblesSeed[radius_, angle_, n_Integer : 10, args___, opts : OptionsPattern[]] :=
Block[{t},
Table[
t = ResourceFunction["RandomScribble"][opts][[1]];
t = GeometricTransformation[t, ScalingMatrix[radius*{1, 1}/RandomReal[{4, 12}]]];
GeometricTransformation[t, TranslationTransform[p]],
{p, RandomPoint[Disk[{0, 0}, radius, {0, angle}], n]}]
]; Multicolumn[
Table[ResourceFunction["RandomMandala"][
"RotationalSymmetryOrder" -> RandomChoice[{5, 6, 7, 12}], "SymmetricSeed" -> False, "SeedFunction" -> (ScribblesSeed[##, "NumberOfStrokes" -> {200, 200}, "RotationAngle" -> {-\[Pi]/6, 2 \[Pi] - \[Pi]/7}, "OrderedStrokePoints" -> True, ColorFunction -> "AlpineColors",
"EnvelopeFunctions" -> Automatic] &), "NumberOfSeedElements" -> RandomChoice[{10, 6, 3}], ImageSize -> 150], 25], 6]](https://www.wolframcloud.com/obj/resourcesystem/images/58e/58e2b1e8-d527-4093-8ca7-fb421e6dc9f3/06783f6dabca96af.png)
