Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Make 2D and 3D graphics with specified polygons and corresponding textures
ResourceFunction["TexturizePolygons"][ps,tsp] makes a 2D or 3D plot for the list of polygons ps using the texture specification tsp. | |
ResourceFunction["TexturizePolygons"][ps] uses a random texture. |
Here, polygons for a dodecahedron are given a random texture:
| In[1]:= |
| Out[2]= |  |
Here is the same texturized dodecahedron, unfolded:
| In[3]:= |
| Out[4]= |  |
The PolyhedronData properties "Net" and "Faces" can be used together with polyhedron names; 2D and 3D graphics are produced, respectively:
| In[5]:= | ![BlockRandom[
ResourceFunction["TexturizePolygons"][{"SnubCube", #}, "Radius" -> Sqrt[{6, 4, 2}], ColorFunction -> "TemperatureMap", ImageSize -> Large],
RandomSeeding -> 12
] & /@ {"Net", "Faces"}](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/74348eafd2af143f.png) |
| Out[5]= |  |
Apply TexturizePolygons over a list of random 2D polygons, translated and rotated for better comprehension:
| In[6]:= | ![SeedRandom[6];
ResourceFunction["TexturizePolygons"][
Table[RotationTransform[i]@
TranslationTransform[{0, 0.4}]@
RandomPolygon[{"ConvexHull", RandomInteger[{3, 6}]}], {i, 0, 2 \[Pi], \[Pi]/4}]]](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/21b69bc8f0434cd6.png) |
| Out[7]= |  |
Here is an example with 3D polygons:
| In[8]:= | ![SeedRandom[12];
ResourceFunction["TexturizePolygons"][
Table[RandomPolygon[3 -> {"ConvexHull", RandomInteger[{3, 6}]}], {i, 0, 2 \[Pi], \[Pi]/4}], Boxed -> True, Axes -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/4cdab5ee9886556d.png) |
| Out[9]= | 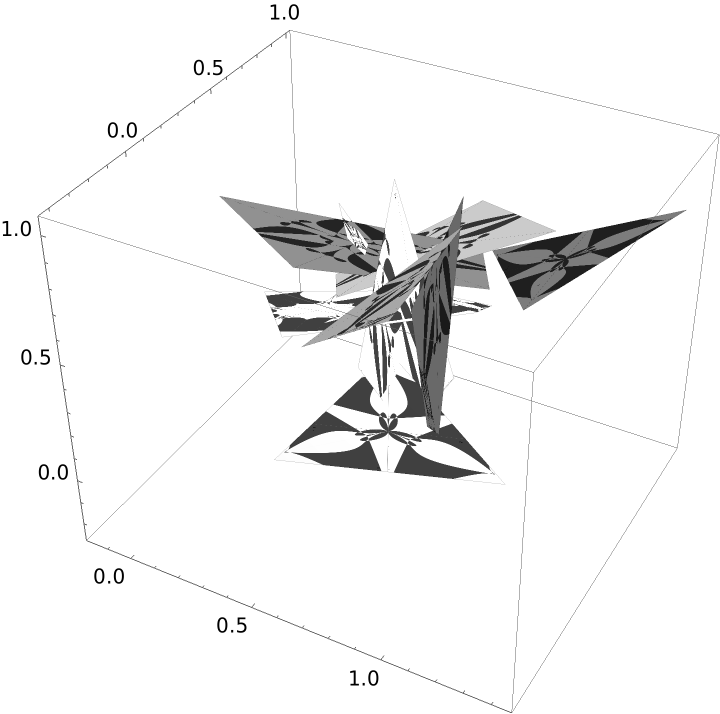 |
The texture specifications Automatic and Random are shortcuts for generating textures using the resource function RandomMandala. Hence, all options of the resource function RandomMandala can be used:
| In[10]:= | ![SeedRandom[66];
ResourceFunction["TexturizePolygons"][{"Cube", "Net"}, Automatic, "RotationalSymmetryOrder" -> 8, "SymmetricSeed" -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/0c73611b06a4e851.png) |
| Out[11]= |  |
| In[12]:= |
| Out[13]= | 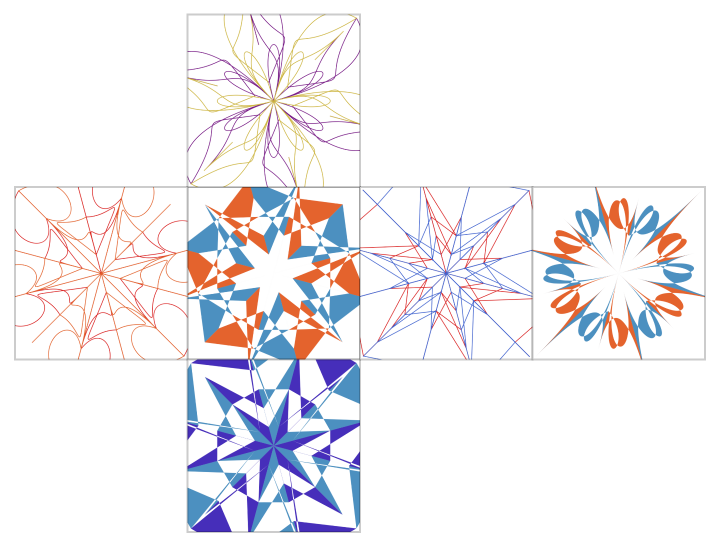 |
The second argument can be a list textures or a list of 2D graphics to be used as textures:
| In[14]:= | ![textures = ExampleData[{"ColorTexture", #}] & /@ {"Ash", "CheetahFur", "Kingwood", "Metal4", "Vavona"};
Magnify[textures, 0.3]](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/1be81d9cfbb6ae41.png) |
| Out[15]= |  |
| In[16]:= |
| Out[16]= |  |
| In[17]:= |
| Out[17]= |  |
The option "Granularity" can be used to control texture mapping. If its value is "NumberOfVertices" then polygons with the same number of vertices have the same textures. If its value is "Polygon" then each polygon it has its own texture according to the texture specification:
| In[18]:= | ![BlockRandom[
ResourceFunction["TexturizePolygons"][{"Cube", "Net"}, Random, ImageSize -> Medium, "Granularity" -> #],
RandomSeeding -> 567
] & /@ {"NumberOfVertices", "Polygon"}](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/6d450ec4874e7374.png) |
| Out[18]= |  |
If the list of graphics for the textures is shorter than the specified list of polygons, the texture graphics list is extended by replicating and catenating:
| In[19]:= | ![SeedRandom[882];
rms = Table[
ResourceFunction["RandomMandala"]["RotationalSymmetryOrder" -> 4, "ConnectingFunction" -> FilledCurve@*BezierCurve, ColorFunction -> "Rainbow"], {6}]](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/78ac615839c1fc84.png) |
| Out[20]= |  |
| In[21]:= | ![BlockRandom[
ResourceFunction["TexturizePolygons"][{"Cube", "Net"}, rms[[#[[1]]]], ImageSize -> Medium, "Granularity" -> #[[2]], PlotLabel -> #],
RandomSeeding -> 121
] & /@ {{All, "NumberOfVertices"}, {All, "Polygon"}, {1 ;; 2, "Polygon"}}](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/1651bd99215ad6ff.png) |
| Out[21]= |  |
The value of the option "VertexTextureCoordinatesFunction" is used to derive the value for VertexTextureCoordinates for each polygon. If the value of "VertexTextureCoordinatesFunction" is Automatic, then the following function is used:
| In[22]:= |
Specialized assignment of the texture coordinates can be done:
| In[23]:= | ![Clear[VTCFunc];
VTCFunc[offset_?NumericQ] := With[{off = offset}, With[{n = Length[First[#1]]}, Table[1/2 {Cos[2 \[Pi] i/n + off], Sin[2 \[Pi] i/n + off]} + {1/
2, 1/2}, {i, 0, n - 1}]] &];](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/18a2d409c120a112.png) |
| In[24]:= | ![Multicolumn[
Table[BlockRandom[
a -> ResourceFunction["TexturizePolygons"]["Cube", "VertexTextureCoordinatesFunction" -> VTCFunc[a], ImageSize -> 200], RandomSeeding -> 9], {a, {0, \[Pi]/4, \[Pi]/10}}], 4]](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/5113ea2f700608aa.png) |
| Out[24]= |  |
Using the option Background can dramatically change the appearance:
| In[25]:= | ![BlockRandom[
ResourceFunction["TexturizePolygons"]["SnubCube", Automatic, "Radius" -> Sqrt[{8, 4, 2}], ColorFunction -> "Rainbow", ImageSize -> Medium, Background -> #], RandomSeeding -> 38] & /@ {Automatic, Black}](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/6dbb2139f51f2d98.png) |
| Out[25]= |  |
Note that if the second argument is Automatic or Random, then the specified background is applied to both the total graphics background and the background of the automatically generated textures.
Place statistical plots on the walls of a polyhedron:
| In[26]:= | ![SeedRandom[232]
data = RandomReal[{0, 10}, {12, 8}];
data = Map[Thread[{Range[Length[#]], #}] &, data];
GraphicsGrid[
List /@ Map[
ResourceFunction["TexturizePolygons"][{"Dodecahedron", #}, SectorChart[#, PolarAxes -> Automatic, PolarGridLines -> Automatic, ImagePadding -> 50] & /@ data, "Granularity" -> "Polygon", "VertexTextureCoordinatesFunction" -> VTCFunc[\[Pi]/12], Method -> {"ShrinkWrap" -> True}] &, {"Faces", "Net"}]]](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/44884777a6255f94.png) |
| Out[29]= | 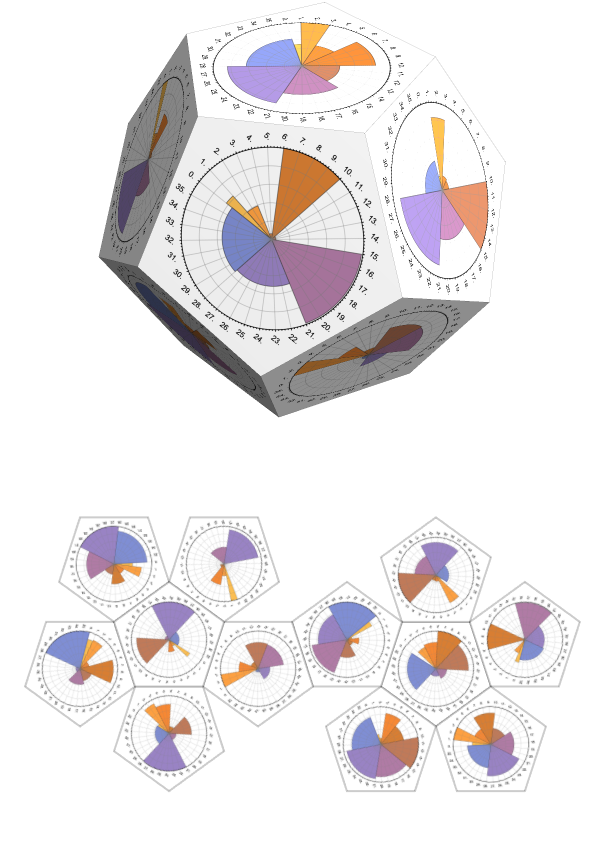 |
Note that in the example above, the number of walls corresponds to the number of rows of the data array; hence, "Granularity"→"Polygon" is used.
For certain data, it might be effective to show different statistical plots on different polyhedron walls:
| In[30]:= | ![SeedRandom[9];
n = 20;
points = Transpose[{RandomReal[{0, 1}, n], RandomReal[{0, 1}, n], RandomVariate[NormalDistribution[10, 2], n]}];
opts = {PlotTheme -> "Scientific", ColorFunction -> "Rainbow", Background -> GrayLevel[0.25], ImagePadding -> 100};
stats = RandomChoice[{BubbleChart[points, opts], PieChart[Sort@points[[All, 3]], opts], Histogram[points[[All, 3]], 6, opts]}, 6]; ResourceFunction[
"TexturizePolygons"][{"Cube", "Faces"}, stats, "Granularity" -> "Polygon", "VertexTextureCoordinatesFunction" -> VTCFunc[\[Pi]/4]]](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/224da79d77f28e6b.png) |
| Out[34]= |  |
If the second argument is Automatic and Random, then the resource function RandomMandala is used; hence, all options taken by that resource function can be specified:
| In[35]:= | ![SeedRandom[43];
GraphicsGrid[{{ResourceFunction["TexturizePolygons"]["Cube", Automatic, "SymmetricSeed" -> False], ResourceFunction["TexturizePolygons"]["Cube", Random, "RotationalSymmetryOrder" -> 8]}}, ImageSize -> Large]](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/50f6cbc8f6174ab7.png) |
| Out[36]= |  |
A table of randomly chosen polyhedra with random mandala textures:
| In[37]:= | ![SeedRandom[62];
Grid@Table[
ResourceFunction["TexturizePolygons"][
RandomChoice[{"SnubCube", "Dodecahedron", "Octahedron", "Cube"}]], 3, 4]](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/5f83fa4414d8a333.png) |
| Out[38]= |  |
Textures over the walls of an unfolded polyhedron:
| In[39]:= | ![SeedRandom[332];
ResourceFunction[
"TexturizePolygons"][{"GreatRhombicosidodecahedron", "Net"}, Automatic, "Radius" -> Sqrt[{8, 6, 4, 2}], ColorFunction -> "Rainbow", ImageSize -> Large]](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/69241a3d426a2ab6.png) |
| Out[40]= |  |
Textures using Chernoff face graphics via the resource function ChernoffFace:
| In[41]:= | ![GraphicsGrid[
List /@ Map[
BlockRandom[
ResourceFunction["TexturizePolygons"][{"Dodecahedron", #}, ResourceFunction["ChernoffFace"][
ColorFunction -> "DarkRainbow"], ImageSize -> Large, Method -> {"ShrinkWrap" -> True}], RandomSeeding -> 359] &, {"Faces", "Net"}]]](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/1110306628bb68d2.png) |
| Out[41]= |  |
Here are some random texturized polyhedra:
| In[42]:= | ![SeedRandom[78663]; GraphicsGrid[
Table[ResourceFunction["TexturizePolygons"][
"GreatRhombicosidodecahedron", Automatic, "Radius" -> Sqrt[{6, 4, 2}], ColorFunction -> "Rainbow", Background -> Black, ImageSize -> Medium, Method -> {"ShrinkWrap" -> True}], 1, 3], Background -> Black, ImageSize -> 1200]](https://www.wolframcloud.com/obj/resourcesystem/images/a64/a6464f47-0762-4c92-a10b-44b00e4864df/5ce40e99f4b7a4f8.png) |
| Out[42]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License