Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 Orthocenter

Source Notebook

Return the orthocenter of a triangle

Contributed by: Ed Pegg Jr

ResourceFunction["Orthocenter"][{p1,p2,p3}]

returns the orthocenter of the triangle defined by vertices p1,p2 and p3.

Details

The orthocenter is the point where all altitudes of a triangle intersect.
ResourceFunction["Orthocenter"][Triangle[{p1,p2,p3}]] is equivalent to ResourceFunction["Orthocenter"][{p1,p2,p3}].

Examples

Basic Examples (2) 

Find the orthocenter of three triangle vertices:

In[1]:=
ResourceFunction["Orthocenter"][{{-1, 0}, {1, -1}, {2, 0}}]
Out[1]=

Show the triangle with its orthocenter and altitudes:

In[2]:=
tri = {{-1, 0}, {1, -2}, {2, 0}}; h = ResourceFunction["Orthocenter"][tri]; Graphics[{EdgeForm[Black], White, Polygon[tri], Green, InfiniteLine[{h, #}] & /@ tri, Blue, Disk[h, .1]}]
Out[2]=

Scope (2) 

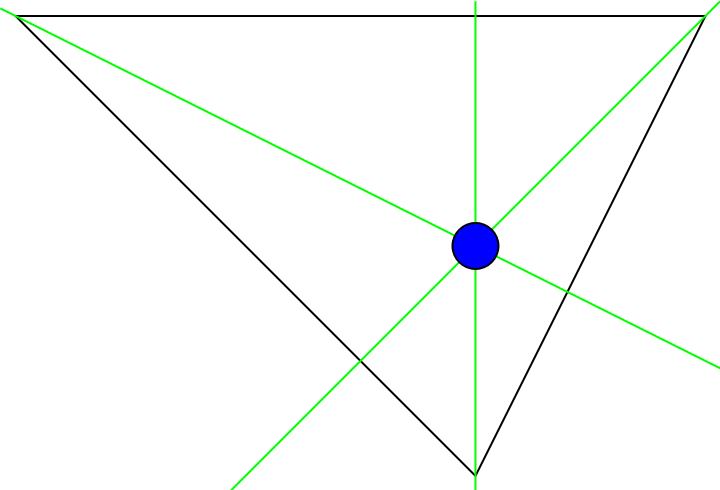Compute the orthocenter of a 3D triangle:

In[3]:=
tri = Triangle[{{0, 0, 0}, {1, 1, 0}, {0, 1, 2}}]; pt = Simplify[ResourceFunction["Orthocenter"][tri]]
Out[3]=

Show the orthocenter and the triangle together:

In[4]:=
Graphics3D[{{Opacity[0.3, Orange], tri}, {AbsolutePointSize[8], Point[pt]}}]
Out[4]=

Neat Examples (1) 

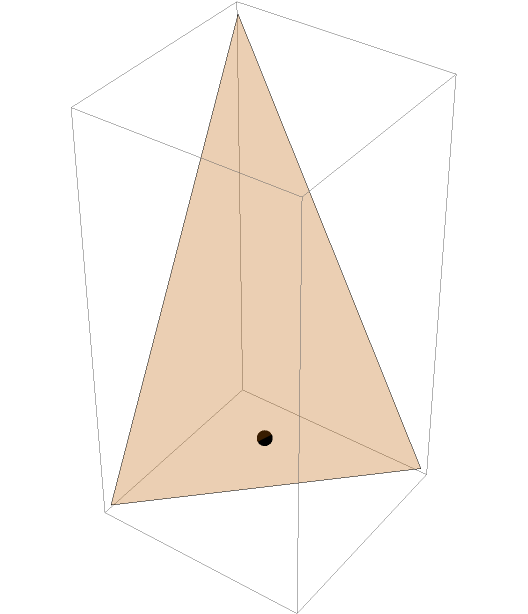When four given points comprise a triangle and its orthocenter, and any three of the points are selected as triangle vertices, the remaining point will be the triangle's orthocenter:

In[5]:=
Reverse[ResourceFunction["Orthocenter"][#] & /@ Subsets[{{2, -1}, {-1, 8}, {-6, -2}, {0, 0}}, {3}]]
Out[5]=
In[6]:=
Reverse[ResourceFunction["Orthocenter"][#] & /@ Subsets[{{-13, -5, 5}, {-5, 11, -11}, {-3, -9, 15}, {-27, -9, 3}}, {3}]]
Out[6]=

Version History

  • 1.1.0 – 24 August 2021
  • 1.0.0 – 16 October 2019

Related Resources

License Information