Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Warning: This resource is provisional

Function Repository Resource:

 ODEViewer (1.0.0) current version: 2.0.0 »

Source Notebook

Dynamically visualize an ordinary differential equation (ODE) or system of ODEs

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["ODEViewer"][eqns, init, deps, {t}]

creates a dynamic visualization and computes properties of the ordinary differential equation system eqns, with initial conditions init, written in terms of dependent variables deps and independent variable t.

ResourceFunction["ODEViewer"][eqns, init, dep, {t, t1, t2}]

creates a dynamic visualization of eqns with t varying from t1 to t2.

Details

Only first order differential equations are allowed.
Nonlinear differential equations are supported.
Stiff systems are supported.
The plot range is computed using SuggestPlotRange.
Sometimes SuggestPlotRange can not give an optimal range.
Locator for the initial values may be outside the graphic.
Eigensystem is computed only for linear equations.
Node types are recognized only for linear equations.
Locators can be dragged, showing changing initial values at the header.
Select Time Series/Slope field to switch between different views of the solutions.
Display options can turn on/off grid lines and the popup menu selects the number of them.
Interval sliders use the Method "Push".
In the case of multiple solutions, only one slope field is plotted.
If integration fails, empty graphics are shown.
When the locator is outside the suggested plot range, it is possible that the corresponding value of time can not be found.
ODEViewer takes the same options as NDSolve.

Examples

Basic Examples (3) 

Visualize the slope field of a simple equation and it's solution for a given initial condition:

In[1]:=
ResourceFunction["ODEViewer", ResourceVersion->"1.0.0"][{x'[t] == x[t] }, {x[0] == 1.5}, {x}, {t, -1, 1}]
Out[1]=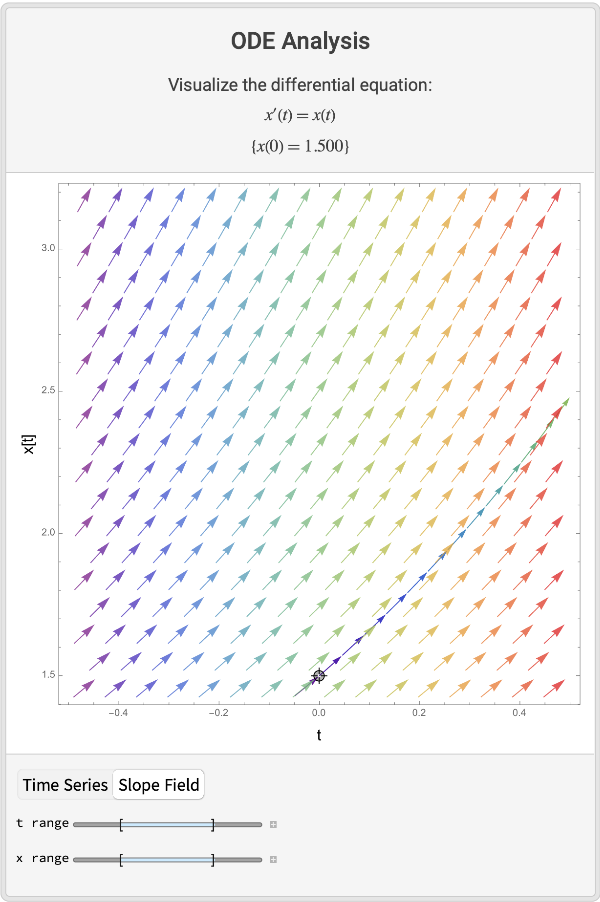

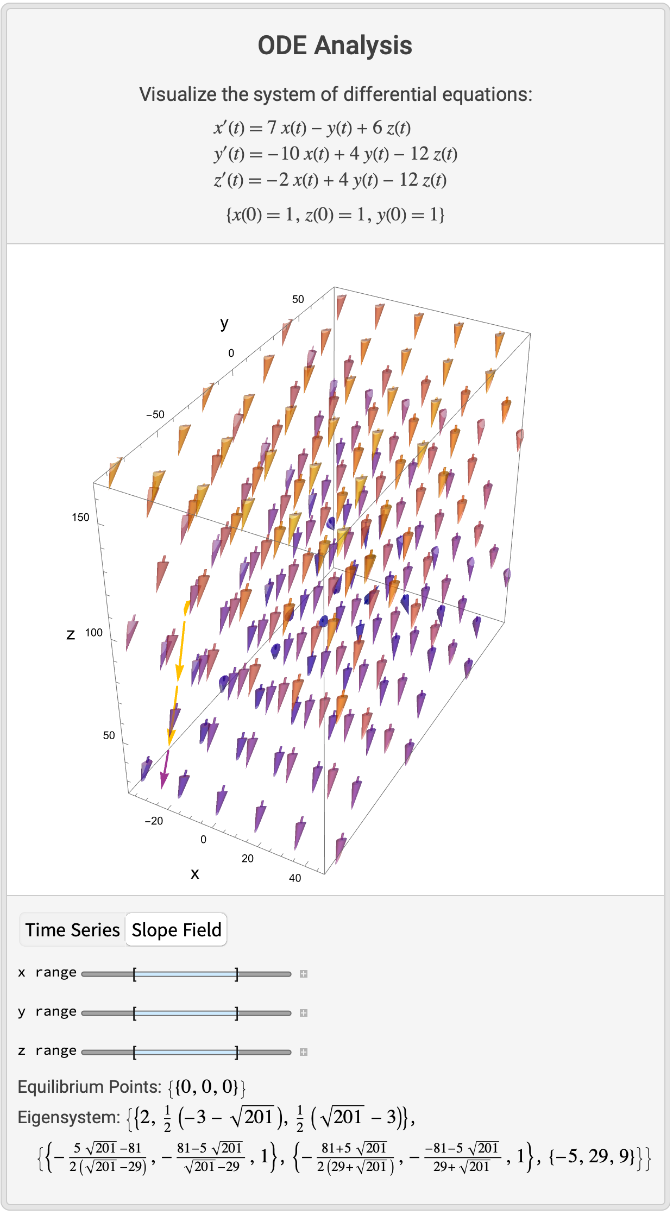
Visualize a system in three dimensions:

In[2]:=
ResourceFunction["ODEViewer", ResourceVersion->"1.0.0"][{Derivative[1][x][t] == 7 x[t] - y[t] + 6 z[t], Derivative[1][y][t] == -10 x[t] + 4 y[t] - 12 z[t], Derivative[1][z][t] == -2 x[t] + 4 y[t] - 12 z[t]}, {x[0] == 1, z[0] == 1, y[0] == 1}, {x, y, z}, {t, 0, 5}]

Visualize the slope field for a non-linear system:

In[3]:=
ResourceFunction["ODEViewer", ResourceVersion->"1.0.0"][{Derivative[1][x][t] == y[t], Derivative[1][y][t] == -x[t] + y[t] (1 - x[t]^2 - 2 y[t]^2)}, {x[ 0] == 1, y[0] == 0}, {x, y}, {t, -1, 1}]
Out[3]=

Scope (2) 

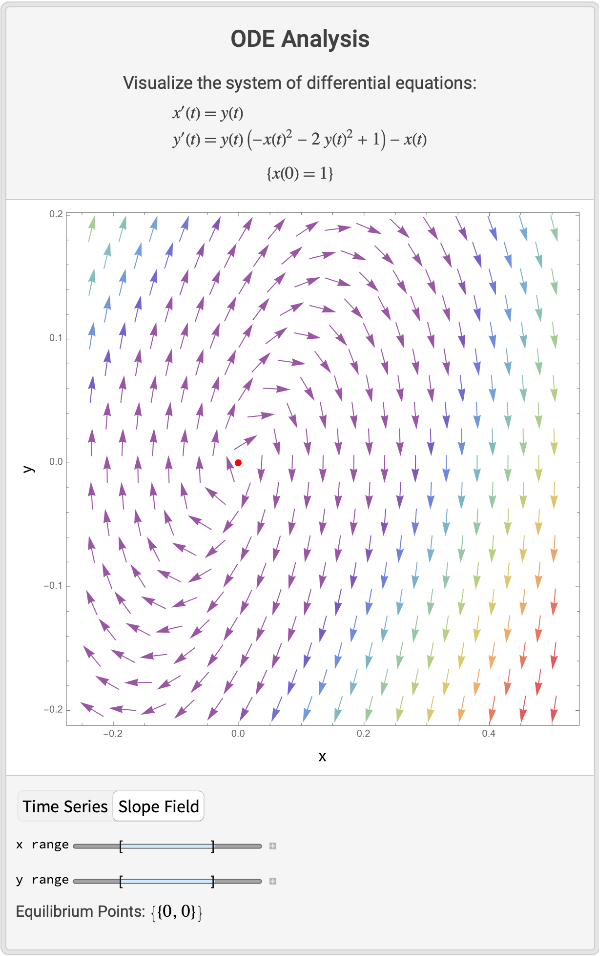A stiff system:

In[4]:=
ResourceFunction["ODEViewer", ResourceVersion->"1.0.0"][{Derivative[1][x][t] == y[t], Derivative[1][y][t] == -x[t] - 2 y[t] - y[t]^3}, {x[0] == 0, y[0] == 1, WhenEvent[y[t] > 10, "StopIntegration"]}, {x, y}, {t, 0, 1}]
Out[4]=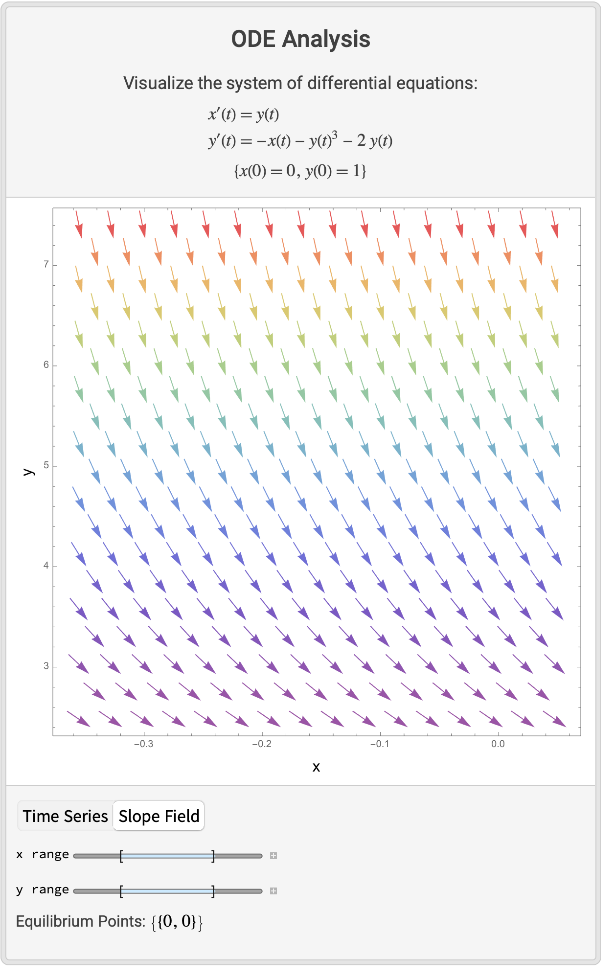

A multiple solution case:

In[5]:=
ResourceFunction["ODEViewer", ResourceVersion->"1.0.0"][{Derivative[1][y][x]^2 - y[x]^2 == 0}, {y[0]^2 == 4}, {y}, {x, .1, 1}]
Out[5]=

Possible Issues (2) 

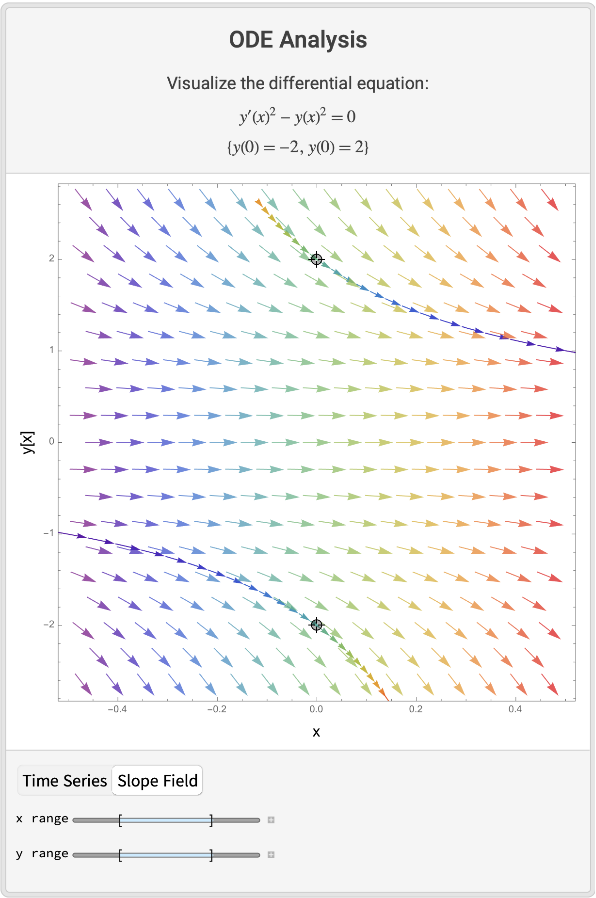A linear system, the plot range is calculated automatically, but the plot range is not optimal:

In[6]:=
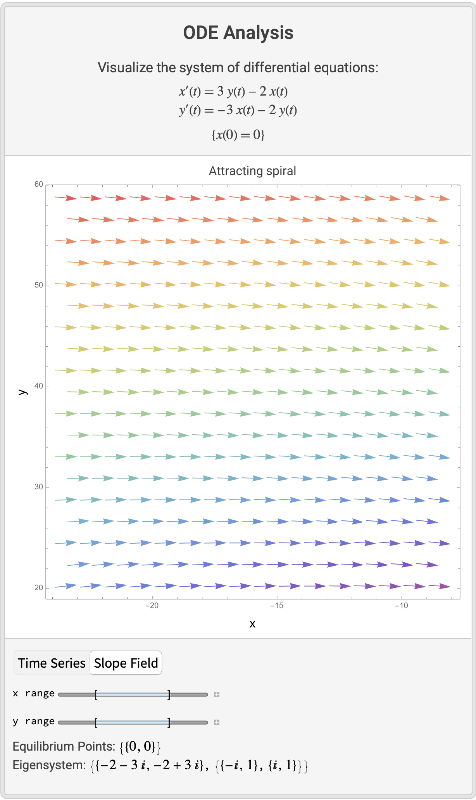
ResourceFunction["ODEViewer", ResourceVersion->"1.0.0"][{Derivative[1][x][t] == -2 x[t] + 3 y[t], Derivative[1][y][t] == -3 x[t] - 2 y[t]}, {x[0] == 0, y[0] == 1}, {x, y}, t]

The same system, with a explicit plot range:

In[7]:=
ResourceFunction["ODEViewer", ResourceVersion->"1.0.0"][{Derivative[1][x][t] == -2 x[t] + 3 y[t], Derivative[1][y][t] == -3 x[t] - 2 y[t]}, {x[0] == 0, y[0] == 1}, {x, y}, {t, -1, 1}]
Out[7]=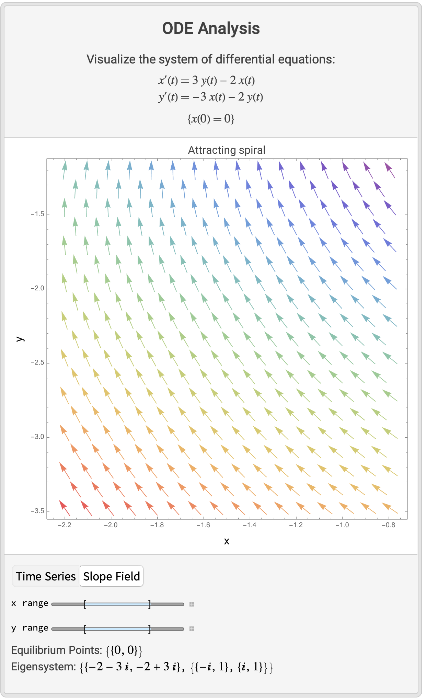

If something fails shows nothing:

In[8]:=
ResourceFunction["ODEViewer", ResourceVersion->"1.0.0"][{Derivative[1][y][x] == (2 (1/x - 1/x^2))/( y[x] - 1/y[x])}, {y[1] == -1}, {y}, {x, .1, 1}]
Out[8]=

Publisher

Wolfram|Alpha Math Team

Version History

  • 2.0.0 – 23 March 2023
  • 1.0.1 – 18 October 2022
  • 1.0.0 – 14 October 2022

Related Resources

Author Notes

To view the full source code for ODEViewer, evaluate the following:

License Information