Function Repository Resource:

NinePointQuadric

Find a quadric surface that passes through nine given 3D points

Contributed by: Ed Pegg Jr

ResourceFunction["NinePointQuadric"][pts,{x,y,z}]

returns the implicit Cartesian equation in the variables x,y and z of the quadric surface that goes through the points pts.

ResourceFunction["NinePointQuadric"][pts]

uses the formal variables x, y and z.

Examples

Basic Examples (3)

Find the quadric surface going through nine points (based of the decimal digits of 9²⁷):

In[1]:=

Out[2]=

Show the quadric surface (a hyperboloid of one sheet) with the points:

In[3]:=

Graphics3D[{ContourPlot3D[
quadric == 0, {x, -3, 12}, {y, -3, 12}, {z, -3, 12}, ContourStyle -> Opacity[0.3]][[1]], {ColorData[97, 4], Sphere[pts, Scaled[0.008]]}}]

Out[3]=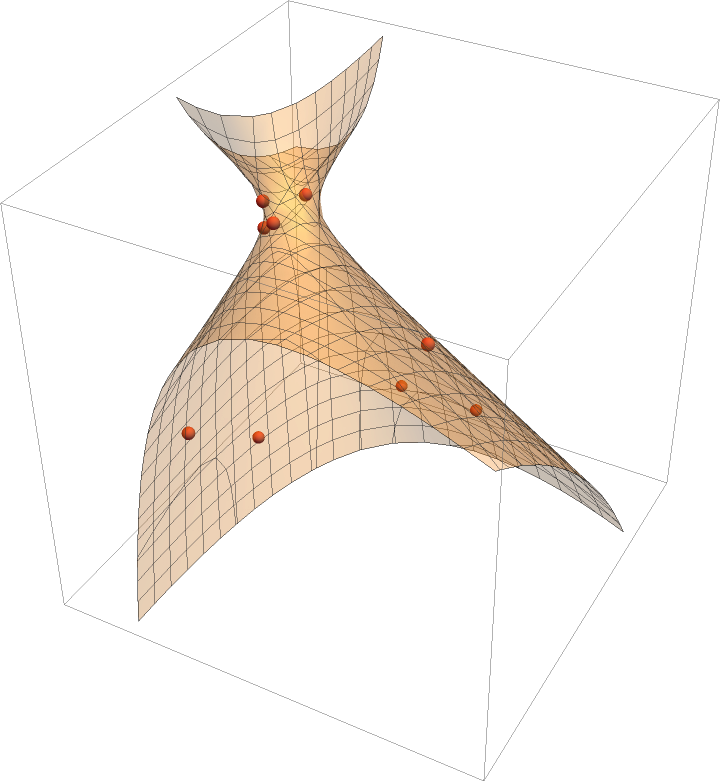

Find the quadric surface going through nine points (based of the decimal digits of 9²⁸):

In[4]:=

$pts = Partition[IntegerDigits[9^28, 10, 27], 3]; quadric = ResourceFunction["NinePointQuadric"][pts, {x, y, z}]$

Out[5]=

Show the quadric surface (a hyperbolic paraboloid) with the points:

In[6]:=

Out[6]=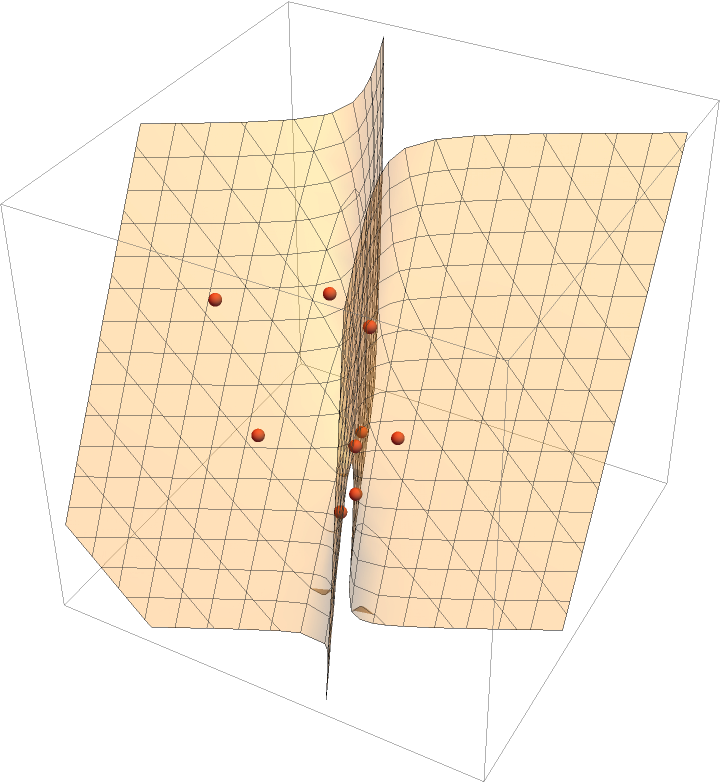

Find the quadric surface going through nine points based of the decimal digits of 9²⁵:

In[7]:=

$pts = Partition[IntegerDigits[9^25, 10, 27], 3]; quadric = ResourceFunction["NinePointQuadric"][pts, {x, y, z}]$

Out[8]=

Show the quadric surface (an ellipsoid) with the points:

In[9]:=

Out[9]=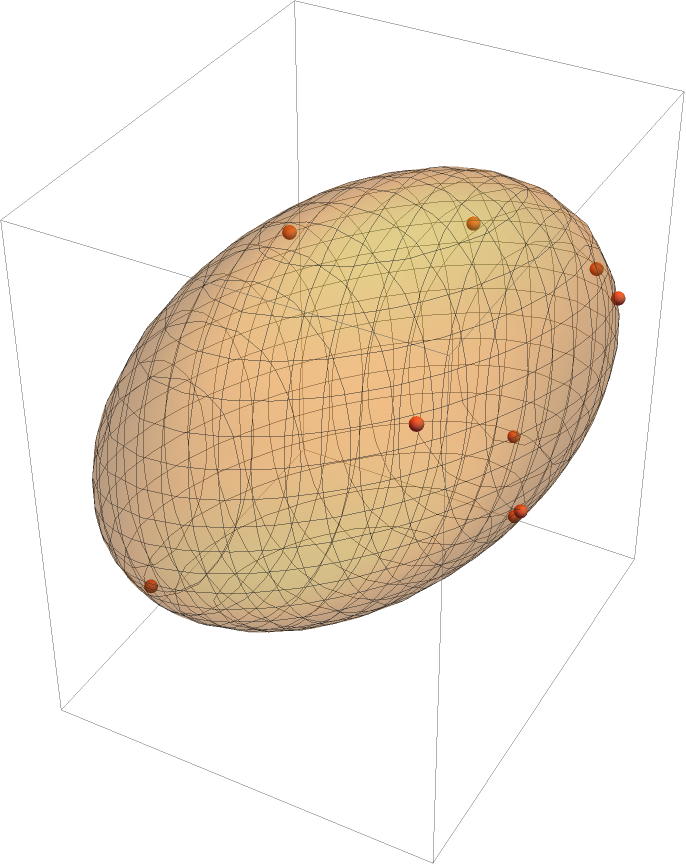

Use the resource function QuadricSurfacePlot to show this same ellipsoid:

In[10]:=

$ResourceFunction["QuadricSurfacePlot"][-7962557 x + 2547673 x^2 - 5905703 y - 2298838 x y + 1732345 y^2 - 7305719 z - 1057140 x z + 629106 y z + 1014353 z^2, {x, y, z}, "DrawAxes" -> True, Mesh -> None]$

Out[10]=

Scope (2)

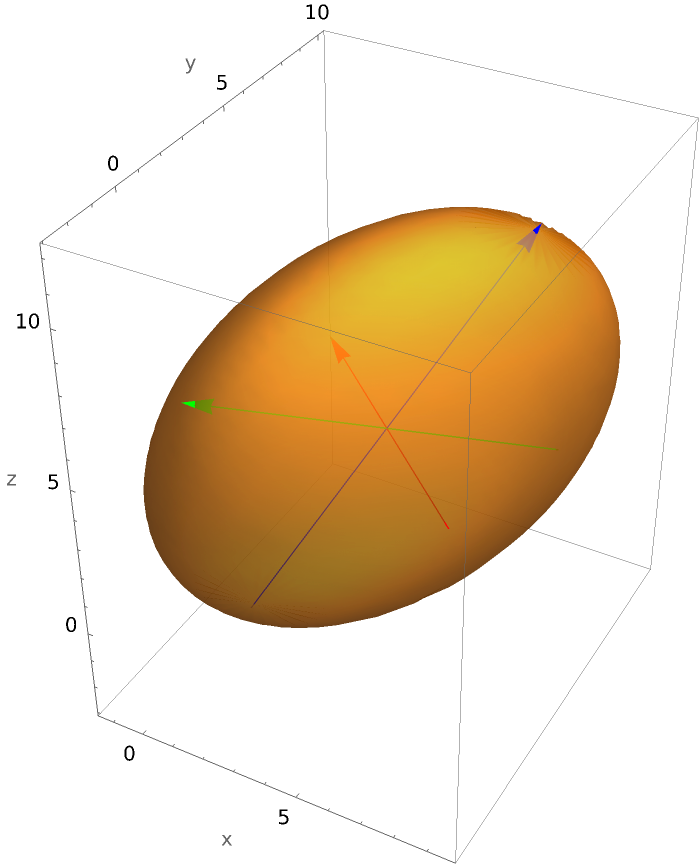Use formal variables:

In[11]:=

Out[11]=

Nine random real points:

In[12]:=

Out[12]=

The quadric through these points:

In[13]:=

Out[13]=

Show the quadric surface (a hyperboloid of 2 sheets) with the points:

In[14]:=

Graphics3D[{ContourPlot3D[
quadric == 0, {x, -4, 4}, {y, -4, 4}, {z, -4, 4}, ContourStyle -> Opacity[0.3]][[1]], {ColorData[97, 4], Sphere[pts, Scaled[0.008]]}}]

Out[14]=

Possible Issues (3)

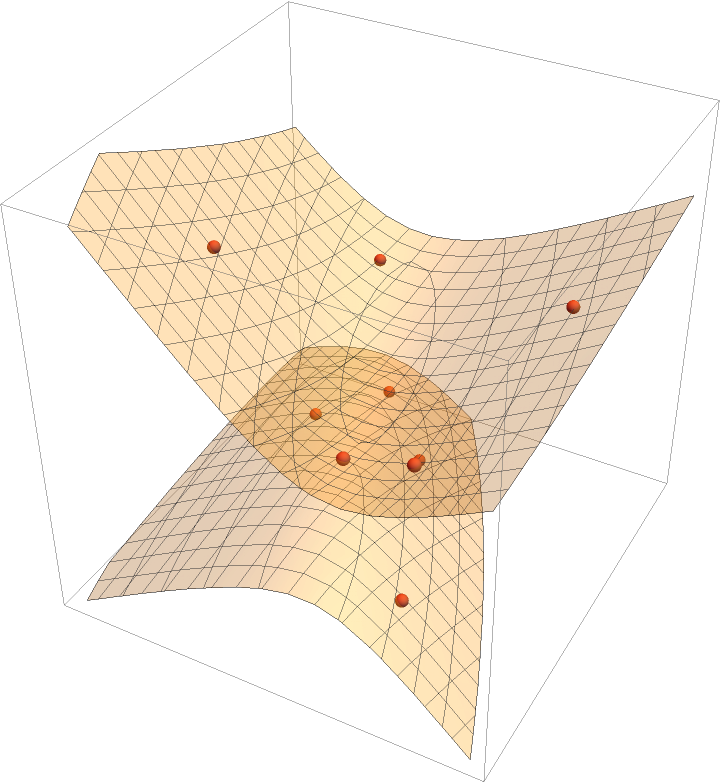Pick nine points on a sphere:

In[15]:=

Out[15]=

Find the surface of the sphere:

In[16]:=

Out[16]=

The following set of nine points should give the same sphere equation, but the matrix method fails due to degeneracy:

In[17]:=

Out[17]=

Version History

1.0.0 – 25 July 2022

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License